1. Background requirements:
We have three kinds of coins with different denominations, 11 yuan, 5 yuan and 1 yuan (there must be). We have to pay 15 yuan (integer). How many coins do we need at least?
At least 3 coins (3 5 yuan coins).
2. Realization of dynamic programming
This problem should be fully suitable for dynamic programming solution: multi-stage decision-making to find the optimal solution.
Idea:
A) , the phases are divided by the face value of the coin. Each phase (the value of each coin) has two situations: use or not use the coin with that face value.
B) , after each decision, a group of States will be generated: how many coins are used in this decision, how many coins are used now, and how much money is left in each state.
C) , record each stage and status with a status table, and find the total number of coins with the remaining money of 0.
Difficulties:
The problem seems simple, but how is the status record form organized? After thinking for a long time, I feel I haven't found a very suitable status record form. First, implement the first version in your own way. Welcome to discuss it.
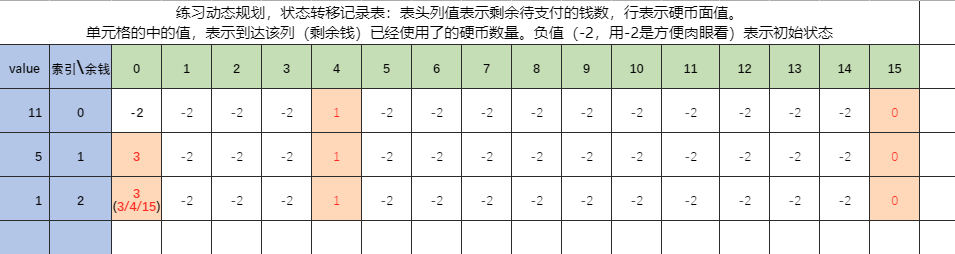
1. Take the face value as the row and the remaining money (integer starting from 0) as the column to generate the status record table.
2. The value in the cell records the sum of how many coins are currently used. The initial state is negative (negative can be any number).
As shown in the figure:
The state transition process is described in detail below:
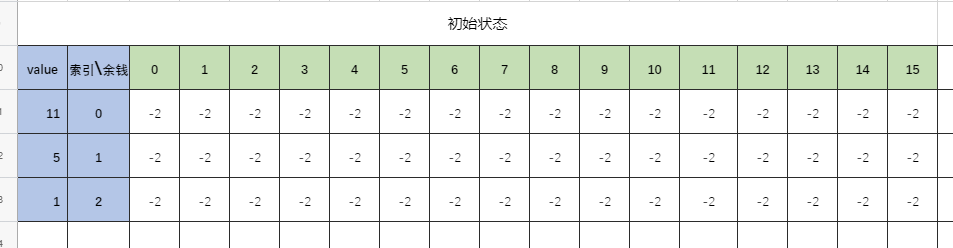
1. In the initial state, create a table: the header column value represents the amount of money remaining to be paid (when it is 0, it means there is no money remaining to be paid), and the row represents the face value of coins.
The value in the cell indicates the number of coins that have been used to reach the column (remaining money). A negative value (- 2, which is convenient for the naked eye) indicates the initial state
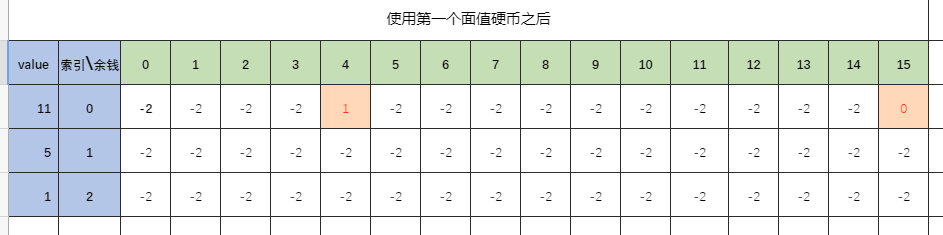
2. For coins with a face value of 11, there are two options: use or not use. If you use it, you can use up to 1 piece, and the remaining 4 pieces need to be paid. If you don't need it, you'll have to pay the remaining 15 yuan. After the decision, the status changes to:
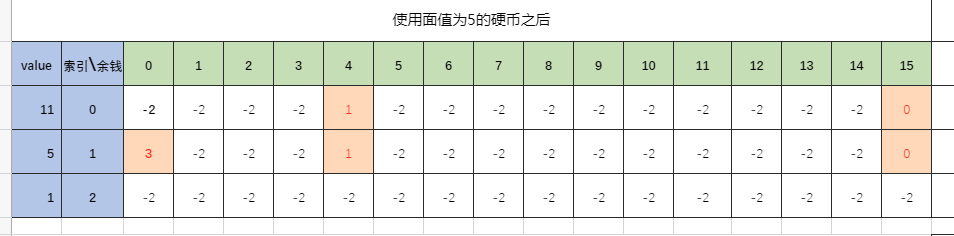
3. Use coins with face value of 5: deduce the next state set based on the previous state set. The remaining money last time was 4 yuan, or 15 yuan. When using the second coin, there are two choices: use or not. When the face value is not used, it is very simple. Just copy the status of the previous line directly. When using, note that if the status data (not - 2) already exists in the cell after use, keep the small value. The status after using face value 2 is:
4. Use coins with face value of 1. The logic is the same as the previous step. The status after using face value of 1 is:
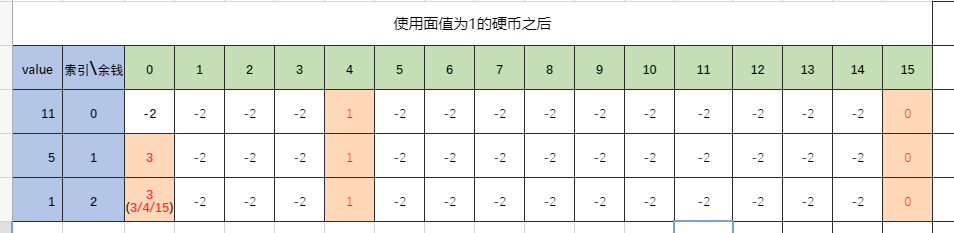
5. At this time, the first element value states[2][0] in the last row of the state table is the value of the optimal solution.
With the above analysis, it is easy to translate into code:
// Need to run in a separate file
/**
* Tool method to create a table (two-dimensional array)
* @param {*} rows
* @param {*} columns
* @param {*} defaultValue
* @returns
*/
function createTableArr(rows, columns, defaultValue =0){
console.log(`createTableArr :: enter, rows = ${rows}, columns = ${columns}, defaultValue = ${defaultValue}`);
const table = [];
for(let i=0; i<rows; i++){
const rowArr = new Array(columns)
rowArr.fill(defaultValue)
table.push(rowArr)
}
return table;
}
/**
* Solve the problem: there are three kinds of RMB with a minimum denomination of 11, 5 and 1, and pay with the least number of sheets
* @param { int[] } values , RMB face value array
* @param {int} totalNeedGive , Quantity to be paid
* @returns {int} minCoinCount, Minimum number of money used
*/
function giveChangeBT(values, totalNeedGive){
const defaultCellValue = -2; // Any negative number can be used here, - 2 is not convenient to see the result state, because - 1 and 1 are too similar.
const states = createTableArr(values.length, totalNeedGive+1, defaultCellValue); // totalNeedGive+1 is because there is a 0 column
// First line under special treatment
states[0][totalNeedGive] = 0; // Do not use the face value
if(totalNeedGive >= values[0]){ // Use this face value
const currentSheet = Math.floor(totalNeedGive/values[0])
const restNeed = totalNeedGive % values[0];
states[0][restNeed] = currentSheet; // The status is the number of records
}
for(let rowIndex = 1; rowIndex < values.length; rowIndex++ ){
// If you don't use this face value, copy the previous line directly. Note: columnIndex is the remaining payment
for(let columnIndex = 0; columnIndex <= totalNeedGive; columnIndex++){
if(states[rowIndex-1][columnIndex] >=0 ){
states[rowIndex][columnIndex] = states[rowIndex-1][columnIndex]; // If you don't use this face value, copy the previous line directly
}
}
// If you use money of that face value. Note: columnIndex is the remaining payment
for(let columnIndex = 1; columnIndex <= totalNeedGive; columnIndex++){
if(states[rowIndex-1][columnIndex] >=0 ){
const currentSheet = Math.floor(columnIndex/values[rowIndex])
const newRest = columnIndex % values[rowIndex];
const total = states[rowIndex-1][columnIndex] + currentSheet // Total number of new sheets
const state = states[rowIndex][newRest] // Number of original RMB sheets in this state
if(state === defaultCellValue){ // This cell has not been used
states[rowIndex][newRest] = total; // The status is the number of records
}else{
if(state > total){ // If the cell has been used, keep the small one
states[rowIndex][newRest] = total; // The status is the number of records
}
}
}
}
}
const minCoinCount = states[states.length - 1][0];
console.log(`giveChangeBT :: end, minCoinCount = ${minCoinCount}, states = `)
// How do you know which denomination and how many pieces are used?... This backward push is a little difficult
console.log(states)
return minCoinCount;
}
const values = [11, 5, 1]; // I think it's in order
const totalNeedGive = 15;
giveChangeBT(values, totalNeedGive);
Continue to go deeper. The minimum number of sheets is calculated above. When the minimum number of sheets is calculated, how many pieces of money of each denomination will be used? If you deduce from the above derivation, it feels so complicated.
Then follow the above idea. When saving the status, you can change the status value from quantity to a status object (e.g. {sum: XX, route: [{coinvalue: XX, sheets: XX}]}). How many pieces of each face value are used in the current stage, such as the status table:

Modify the above implementation:
// Run in the same file as the above code
/**
* There are three kinds of RMB with minimum denominations of 11, 5 and 1. Pay with the minimum number of sheets. Return the minimum number of sheets and specific payment details. How many sheets are used for each denomination.
* @param { int[] } values , RMB face value array
* @param {int} totalNeedGive , Quantity to be paid
* @returns {Object} result, The minimum amount of money used and detailed records
*/
function giveChangeBT2(values, totalNeedGive){
const defaultCellValue = -2; // Any negative number can be used here, - 2 is not convenient to see the result state, because - 1 and 1 are too similar.
const states = createTableArr(values.length, totalNeedGive+1, defaultCellValue) // You need to copy the above public methods
// First line under special treatment
states[0][totalNeedGive] = {sum:0, route:[]}; // Do not use the face value
if(totalNeedGive >= values[0]){ // Use this face value
const currentSheet = Math.floor(totalNeedGive/values[0])
const restNeed = totalNeedGive % values[0];
states[0][restNeed] = {sum:currentSheet, route:[{coinValue: values[0], sheets: currentSheet}]} ; // The status is the number of records
}
for(let rowIndex = 1; rowIndex < values.length; rowIndex++ ){
// If you don't use this face value, copy the previous line directly. Note: columnIndex is the remaining payment
for(let columnIndex = 0; columnIndex <= totalNeedGive; columnIndex++) {
if(states[rowIndex-1][columnIndex] !== defaultCellValue ){
states[rowIndex][columnIndex] = states[rowIndex-1][columnIndex]; // If you don't use this face value, copy the previous line directly
console.log(rowIndex, columnIndex, states[rowIndex][columnIndex])
}
}
// If you use money of that face value. Note: columnIndex is the remaining payment
for(let columnIndex = 1; columnIndex <= totalNeedGive; columnIndex++){
if(states[rowIndex-1][columnIndex] !== defaultCellValue ){
const currentSheet = Math.floor(columnIndex/values[rowIndex])
const newRest = columnIndex % values[rowIndex];
const total = states[rowIndex-1][columnIndex].sum + currentSheet // Total number of new sheets
const state = states[rowIndex][newRest]
const newRoute = [...states[rowIndex-1][columnIndex].route]
newRoute.push({coinValue: values[rowIndex], sheets: currentSheet})
if(state === defaultCellValue){ // Number of original RMB sheets in this state
states[rowIndex][newRest] = {sum:total, route:newRoute}; // The status is the number of records and the path
}else{
if(state.sum > total){
const newRoute = [...state.route];
newRoute.push({coinValue: values[rowIndex], sheets: currentSheet})
states[rowIndex][newRest] = {sum:total, route:newRoute} ; // The status is the number of records and the path
}
}
}
}
}
// console.log(states)
const result = states[values.length-1][0];
console.log(`giveChangeBT2 :: end, result = `)
console.log(result)
return result
}
giveChangeBT2(values, totalNeedGive);3. Implementation based on Backtracking
The logic of backtracking is not complex. It is recursion. There are two choices each time, whether to use or not.
// It needs to be run in a separate file, otherwise there will be duplicate variable names.
/**
* Using backtracking algorithm to search the optimal solution
* @param { int[] } values , RMB face value array
* @param {int} rest , Amount of money remaining to be paid
* @param {*} index, Index of the array where the currently used RMB face value is located
* @param {*} sheets , The total number of RMB sheets used at the current stage
* @param {*} routes , The detailed process records how many pieces of money are used for each denomination at the current stage.
* @returns
*/
let minSheets = Infinity; // Record the minimum number of change sheets
let minRoutes;
function giveChangeBT(values, rest, index=0, sheets=0, routes=[]){
if(rest ===0){
console.log(`giveChangeBT :: end, rest = ${rest}, index = ${index}, sheets = ${sheets}`)
console.log(routes)
if(sheets >0 && minSheets > sheets){
minSheets = sheets;
minRoutes = routes;
}
return sheets;
}
// Do not use up the available currencies.
if(index<values.length){
// Do not use RMB of this face value
const newRotes = [...routes] // This step is very important. The details should be copied
giveChangeBT(values, rest, index+1, sheets, newRotes)
// In RMB of this face value
const maxSheets = Math.floor(rest/values[index]);
const newRest = rest%values[index];
// Assist to see the specific details
const route = {
[values[index]] : maxSheets,
}
newRotes.push(route);
giveChangeBT(values, newRest, index+1, sheets+maxSheets, newRotes)
}
}
const values = [11, 5, 1]; // I think it's in order
const totalNeedGive = 15;
giveChangeBT(values, totalNeedGive)
console.log(minSheets, minRoutes) // 3 [ { '5': 3 } ]4. Implementation of greedy algorithm
To simplify the logic, it is considered that the face values array has been sorted from large to small. Greed is to try to pay with the maximum face value at each step.
/**
* Implementation of greedy algorithm
* @param { int[] } values , The RMB face value array is considered to be arranged from large to small.
* @param {int} rest , Amount of money remaining to be paid
* @param {*} index, Index of the array where the currently used RMB face value is located
* @param {*} sheets , The total number of RMB sheets used at the current stage
* @param {*} routes , The detailed process records how many pieces of money are used for each denomination at the current stage.
* @returns
*/
function giveChangeTX(values, rest, index=0, sheets=0, routes=[]){
if(rest ===0 || index >= values.length){
console.log(`giveChangeTX :: end, rest = ${rest}, index = ${index}, sheets = ${sheets}`)
console.log(routes)
return sheets;
}
// With greedy thinking, first find the one with the largest denomination, because the denomination is the largest, and the number of sheets required will be "less"
const maxSheets = Math.floor(rest/values[index]);
const newRest = rest%values[index];
// Assist to see the specific details
const route = {
[values[index]] : maxSheets,
}
const newRotes = [...routes, route];
return giveChangeTX(values, newRest, index+1, maxSheets+sheets, newRotes)
}
giveChangeTX([11, 5, 1], 15);
// output
// giveChangeTX :: end, rest = 0, index = 3, sheets = 5
// [ { '11': 1 }, { '5': 0 }, { '1': 4 } ]