Chapter 9 optimization methods and regularization
Almost all deep learning is supported by a very important algorithm: random gradient descent (SGD).
So far, we have a deep understanding of the concept of parametric learning. In the past few chapters, we have discussed the concept of parametric learning and how this type of learning enables us to define scoring functions that map input data to output class labels.
This scoring function is defined according to two important parameters; Specifically, our weight matrix W and our bias vector b. Our scoring function takes these parameters as input and returns the prediction of each input data point Xi.
We also discuss two common loss functions: multi class SVM loss and cross entropy loss. At the most basic level, the loss function is used to quantify the "good" or "bad" degree of a given predictor (i.e. a set of parameters) in classifying the input data points in our data.
Given these modules, we can now turn to the most important aspect of machine learning, neural networks and deep learning - optimization. Optimization algorithm is an engine that provides power for neural networks and enables them to learn patterns from data. Throughout the discussion, we learned that obtaining a high-precision classifier depends on finding a set of weights W and b so that our data points can be classified correctly.
But how do we find and obtain the weight matrix W and bias vector b with high classification accuracy? Do we initialize them randomly and evaluate them over and over again, hoping that at some time we can get a set of parameters to obtain a reasonable classification? We can - but given that the number of parameters of modern deep learning networks reaches tens of millions, it may take a long time to blindly and accidentally find a reasonable set of parameters.
Instead of relying on pure randomness, we also need to define an optimization algorithm so that we can literally improve W and b. In this chapter, we will study the most commonly used algorithm for training neural networks and deep learning models - gradient descent. There are many variations of gradient descent (we will also cover it), but in each case, the idea is the same: iteratively evaluate your parameters, calculate your loss, and then take a small step towards minimizing your loss.
1, Gradient descent
Gradient descent algorithm has two main styles:
1. Vanilla gradient descent
2. The more commonly used optimized "random" version.
In this section, we will review the basic Vanilla implementation to form a baseline for our understanding. After we understand the basics of gradient descent, we will move to the random version. Then, we will review some "knowledge points" in gradient descent, including momentum and Nesterov acceleration.
1.1 loss and optimization surface
Gradient descent method is an iterative optimization algorithm, which runs on the loss range (also known as the optimization surface). An example of gauge gradient descent is to visualize our weight along the x axis and then the loss of a given set of weights along the y axis.
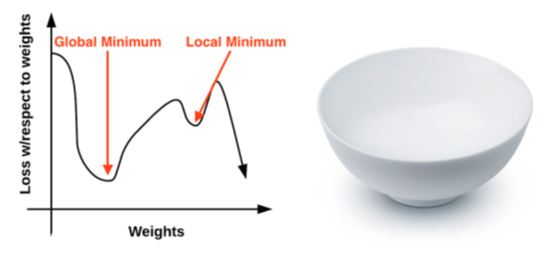
Given a set of parameters w (weight matrix) and b (offset vector), each position along the bowl surface corresponds to a specific loss value. Our goal is to try different values of W and b, evaluate their losses, and then take a step towards a more optimized value with lower losses (ideally).
1.2 gradient in gradient descent
Left: our robot Chad. Right: Chad's job is to navigate our loss landscape and descend to the bottom of the basin. Unfortunately, the only sensor Chad can use to control his navigation is a special function called the loss function L. This function must direct him to a lower loss area.
Now Chad's job is to navigate to the bottom of the basin (where the loss is minimal). Does it look easy? All Chad has to do is adjust his direction so that he faces the "downhill" and slides along the slope until he reaches the bottom of the bowl.
But the problem is: Chad is not a very smart robot. Chad has only one sensor - this sensor allows him to take his parameters W and b and calculate a loss function L. Therefore, Chad can calculate his relative position in the lost landscape, but he has no idea in which direction he should take a step to get himself close to the bottom of the basin.
What's Chad doing? The answer is to apply gradient descent. All Chad needs to do is follow the slope of gradient W. We can calculate the gradient w for all dimensions using the following equation:
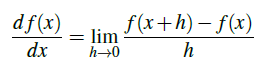
In > 1 dimension, our gradient becomes a vector of partial derivatives. The problem with this equation is:
1. It is an approximation of the gradient.
2. Very slow.
1.3 treat it as a convex problem
Using the bowl in the figure as the visualization of the loss situation also enables us to draw an important conclusion in modern neural networks - we regard the loss situation as a convex problem, even if it is not. If a function F is convex, all local minima are also global minima. This idea is very suitable for bowl visualization. Our optimization algorithm only needs to tie a pair of skis to the top of the bowl, and then slide down the slope slowly until we reach the bottom.
The problem is that almost all the problems we use neural networks and deep learning algorithms are not neat convex functions. On the contrary, in this bowl, we will find peaked peaks, valleys more similar to canyons, steep declines, and even troughs where losses fall sharply but rise sharply again.
Given the nonconvex nature of our dataset, why should we apply gradient descent? The answer is simple: because it's done well enough. Quote goodflow et al. [10]:
"[An] optimization algorithm may not guarantee to reach the local minimum in a reasonable time, but it usually finds the very low value of the [loss] function fast enough for use."
When training deep learning networks, we can set high expectations to find local / global minima, but this expectation is rarely consistent with reality. On the contrary, we finally found a low loss region - this region may not even be a local minimum, but in practice, it has proved to be sufficient.
1.4 deviation techniques
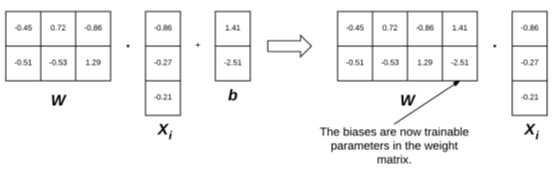Left: usually, we regard the weight matrix and bias vector as two independent parameters. Right: however, we can actually embed the bias vector into the weight matrix (thus making it a trainable parameter directly in the weight matrix by initializing our weight matrix with an additional column).
1.5 gradient descent pseudo code
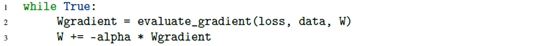
1.6 basic gradient descent using Python
gradient_descent.py: the code is as follows:
# import the necessary packages
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
import numpy as np
import argparse
def sigmoid_activation(x):
# compute the sigmoid activation value for a given input
return 1.0 / (1 + np.exp(-x))
def sigmoid_deriv(x):
# compute the derivative of the sigmoid function ASSUMING
# that the input `x` has already been passed through the sigmoid
# activation function
return x * (1 - x)
def predict(X, W):
# take the dot product between our features and weight matrix
preds = sigmoid_activation(X.dot(W))
# apply a step function to threshold the outputs to binary
# class labels
preds[preds <= 0.5] = 0
preds[preds > 0] = 1
# return the predictions
return preds
# construct the argument parse and parse the arguments
ap = argparse.ArgumentParser()
ap.add_argument("-e", "--epochs", type=float, default=100,
help="# of epochs")
ap.add_argument("-a", "--alpha", type=float, default=0.01,
help="learning rate")
args = vars(ap.parse_args())
# generate a 2-class classification problem with 1,000 data points,
# where each data point is a 2D feature vector
(X, y) = make_blobs(n_samples=1000, n_features=2, centers=2,
cluster_std=1.5, random_state=1)
y = y.reshape((y.shape[0], 1))
# insert a column of 1's as the last entry in the feature
# matrix -- this little trick allows us to treat the bias
# as a trainable parameter within the weight matrix
X = np.c_[X, np.ones((X.shape[0]))]
# partition the data into training and testing splits using 50% of
# the data for training and the remaining 50% for testing
(trainX, testX, trainY, testY) = train_test_split(X, y, test_size=0.5, random_state=42)
# initialize our weight matrix and list of losses
print("[INFO] training...")
W = np.random.randn(X.shape[1], 1)
losses = []
# loop over the desired number of epochs
for epoch in np.arange(0, args["epochs"]):
# take the dot product between our features "X" and the weight
# matrix "W", then pass this value through our sigmoid activation
# function, thereby giving us our predictions on the dataset
preds = sigmoid_activation(trainX.dot(W))
# now that we have our predictions, we need to determine the
# "error", which is the difference between our predictions and
# the true values
error = preds - trainY
loss = np.sum(error ** 2)
losses.append(loss)
# the gradient descent update is the dot product between our
# (1) features and (2) the error of the sigmoid derivative of
# our predictions
d = error * sigmoid_deriv(preds)
gradient = trainX.T.dot(d)
# in the update stage, all we need to do is "nudge" the weight
# matrix in the negative direction of the gradient (hence the
# term "gradient descent" by taking a small step towards a set
# of "more optimal" parameters
W += -args["alpha"] * gradient
# check to see if an update should be displayed
if epoch == 0 or (epoch + 1) % 5 == 0:
print("[INFO] epoch={}, loss={:.7f}".format(int(epoch + 1), loss))
# evaluate our model
print("[INFO] evaluating...")
preds = predict(testX, W)
print(classification_report(testY, preds))
# plot the (testing) classification data
plt.style.use("ggplot")
plt.figure()
plt.title("Data")
plt.scatter(testX[:, 0], testX[:, 1], marker="o", c=testY[:, 0], s=30)
# construct a figure that plots the loss over time
plt.style.use("ggplot")
plt.figure()
plt.plot(np.arange(0, args["epochs"]), losses)
plt.title("Training Loss")
plt.xlabel("Epoch #")
plt.ylabel("Loss")
plt.show()1.7 simple gradient descent results
2, Random gradient descent SGD
In the previous section, we discussed gradient descent, a first-order optimization algorithm that can be used to learn a set of classifier weights for parametric learning. However, the "normal" implementation of this gradient descent may run very slowly on large data sets - in fact, it can even be considered a waste of computation.
Instead, we should apply random gradient descent (SGD), which is a simple modification of the standard gradient descent algorithm, which calculates the gradient and updates the weight matrix W of small batch training data, rather than the whole training set. Although this modification will lead to "more noisy" updates, it also allows us to take more steps along the gradient (one step per batch instead of one step per stage) eventually leads to faster convergence without negative impact on loss and classification accuracy.
SGD can be said to be the most important algorithm for training deep neural networks. Although the original version of SGD was introduced 57 years ago [85], it is still an engine that enables us to train large networks to learn patterns from data points. The most important thing is to take some time to understand SGD for all other algorithms covered in this book.
2.1 small batch SGD
2.2 realize small batch SGD
sgd.py, the code is as follows:
# import the necessary packages
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
import numpy as np
import argparse
def sigmoid_activation(x):
# compute the sigmoid activation value for a given input
return 1.0 / (1 + np.exp(-x))
def sigmoid_deriv(x):
# compute the derivative of the sigmoid function ASSUMING
# that the input "x" has already been passed through the sigmoid
# activation function
return x * (1 - x)
def predict(X, W):
# take the dot product between our features and weight matrix
preds = sigmoid_activation(X.dot(W))
# apply a step function to threshold the outputs to binary
# class labels
preds[preds <= 0.5] = 0
preds[preds > 0] = 1
# return the predictions
return preds
def next_batch(X, y, batchSize):
# loop over our dataset "X" in mini-batches, yielding a tuple of
# the current batched data and labels
for i in np.arange(0, X.shape[0], batchSize):
yield (X[i:i + batchSize], y[i:i + batchSize])
# construct the argument parse and parse the arguments
ap = argparse.ArgumentParser()
ap.add_argument("-e", "--epochs", type=float, default=100,
help="# of epochs")
ap.add_argument("-a", "--alpha", type=float, default=0.01,
help="learning rate")
ap.add_argument("-b", "--batch-size", type=int, default=32,
help="size of SGD mini-batches")
args = vars(ap.parse_args())
# generate a 2-class classification problem with 1,000 data points,
# where each data point is a 2D feature vector
(X, y) = make_blobs(n_samples=1000, n_features=2, centers=2,
cluster_std=1.5, random_state=1)
y = y.reshape((y.shape[0], 1))
# insert a column of 1's as the last entry in the feature
# matrix -- this little trick allows us to treat the bias
# as a trainable parameter within the weight matrix
X = np.c_[X, np.ones((X.shape[0]))]
# partition the data into training and testing splits using 50% of
# the data for training and the remaining 50% for testing
(trainX, testX, trainY, testY) = train_test_split(X, y,
test_size=0.5, random_state=42)
# initialize our weight matrix and list of losses
print("[INFO] training...")
W = np.random.randn(X.shape[1], 1)
losses = []
# loop over the desired number of epochs
for epoch in np.arange(0, args["epochs"]):
# initialize the total loss for the epoch
epochLoss = []
# loop over our data in batches
for (batchX, batchY) in next_batch(trainX, trainY, args["batch_size"]):
# take the dot product between our current batch of features
# and the weight matrix, then pass this value through our
# activation function
preds = sigmoid_activation(batchX.dot(W))
# now that we have our predictions, we need to determine the
# "error", which is the difference between our predictions
# and the true values
error = preds - batchY
epochLoss.append(np.sum(error ** 2))
# the gradient descent update is the dot product between our
# (1) current batch and (2) the error of the sigmoid
# derivative of our predictions
d = error * sigmoid_deriv(preds)
gradient = batchX.T.dot(d)
# in the update stage, all we need to do is "nudge" the
# weight matrix in the negative direction of the gradient
# (hence the term "gradient descent" by taking a small step
# towards a set of "more optimal" parameters
W += -args["alpha"] * gradient
# update our loss history by taking the average loss across all
# batches
loss = np.average(epochLoss)
losses.append(loss)
# check to see if an update should be displayed
if epoch == 0 or (epoch + 1) % 5 == 0:
print("[INFO] epoch={}, loss={:.7f}".format(int(epoch + 1), loss))
# evaluate our model
print("[INFO] evaluating...")
preds = predict(testX, W)
print(classification_report(testY, preds))
# plot the (testing) classification data
plt.style.use("ggplot")
plt.figure()
plt.title("Data")
plt.scatter(testX[:, 0], testX[:, 1], marker="o", c=testY[:, 0], s=30)
# construct a figure that plots the loss over time
plt.style.use("ggplot")
plt.figure()
plt.plot(np.arange(0, args["epochs"]), losses)
plt.title("Training Loss")
plt.xlabel("Epoch #")
plt.ylabel("Loss")
plt.show()2.3SGD results
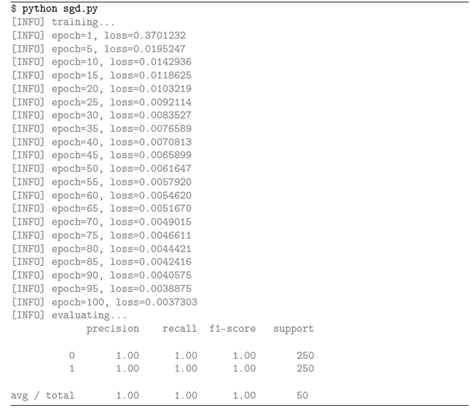
3, Regularization
4.1 what is regularization and why?
Regularization helps us control the model capacity and ensure that our model can better classify untrained data points. We call it generalization ability. If we do not apply regularization, our classifier is easy to become too complex and over fit our training data. In this case, we will lose generalization to our test data (and data points outside the test set, such as new images).
However, too much regularization can be a bad thing. We may risk under fitting. In this case, our model performs poorly on the training data and is unable to model the relationship between the input data and the output category label (because we limit the model capacity too much).
4.2 types of regularization techniques
In general, you will see three common types of regularization directly applied to loss functions. First, we reviewed earlier, L2 regularization (also known as "weight attenuation"):
We also have L1 regularization, which uses absolute values instead of squares:
ElasticNet[98] regularization attempts to combine L1 and L2 regularization:
