🎈 Author: Linux Ape
🎈 Introduction: CSDN Blog Expert 🏆, Huawei Yunheen Expert 🏆, Linux, C/C++, interviews, refreshes, algorithms although consulting me, follow me, have questions and chat privately!
🎈 Focus column: Illustrating data structures and algorithms (The quality of good writing is continuously updated...) 🚀
🎈 Welcome to your friends 👍, Collection ⭐, Leaving a message. 💬
Catalog
✨ 2.5 Heap Adjustment Principle
✨ 3.2 Seek the Front Elements of high frequency k
🍓 1. What is a heap
A heap is a type of binary tree. It is a complete binary tree. A heap is divided into a large top heap and a small top heap, where any node is larger than its left and right child nodes, and a small top heap where any node is larger than its left and right child nodes, as shown below:
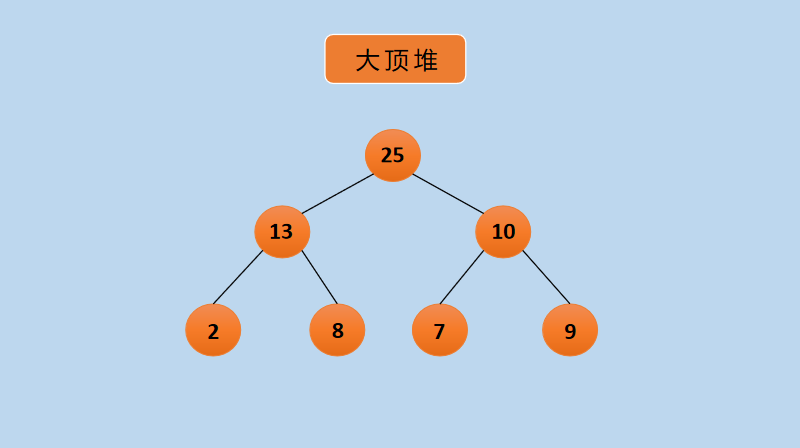 Figure 1 Large Top Heap
Figure 1 Large Top Heap
In the figure above, each node has a value greater than the left and right child nodes, for example, 25 is greater than 13 and 10, 13 is greater than 2 and 8, and so on.
Use the data above to build a small top heap, as follows:
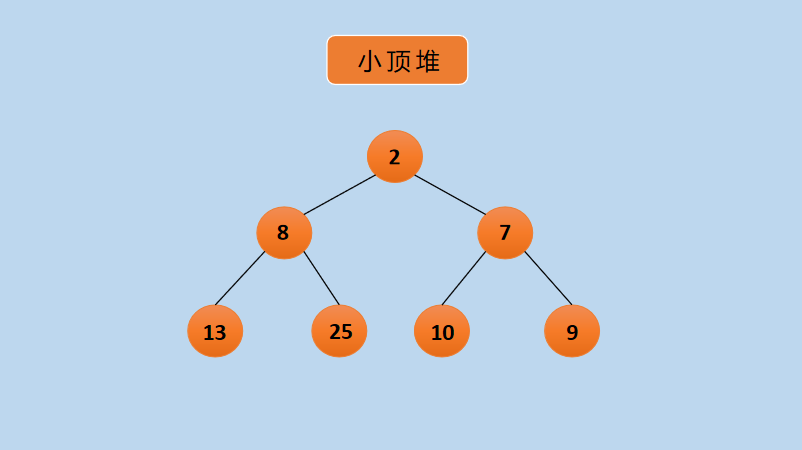 Figure 2 Small Top Heap
Figure 2 Small Top Heap
In the small top heap above, each node is smaller than the left and right child nodes. It doesn't matter who is the older or the smaller of the left and right child nodes. The key point is that it can't be larger than the parent node. As you can see, 2 is smaller than the child nodes 8 and 7, and 8 is smaller than the child nodes 13 and 25.
🔶🔶🔶🔶🔶 I am a dividing line 🔶🔶🔶🔶🔶
🍓 2. Heap Sorting
This is illustrated with the Big Top heap as an example.
✨ 2.1 Algorithmic Principles
Compose the elements to be sorted into a large top heap, take out the top elements (the top is the largest element) each time, make the last element the top node of the heap, readjust the heap so that it becomes a large top heap, and swap the top elements again until all elements are sorted, thus sorting the data.
✨ 2.2 Algorithmic steps
(1) Build a large top heap of elements to be sorted;
(2) The last node exchanges with the root node, at which point it is no longer a big top heap;
(3) Re-adjusting the heap to a large top heap;
(4) Repeat steps 2 to 3 until all elements are in order.
✨ 2.3 Instance Demo
Let's look at an example.
Suppose there is A[] = {10, 8, 9, 2, 13, 7, 25}, where the large top heap is used as an example to sort from small to large.
(1) Initial heap, as follows:
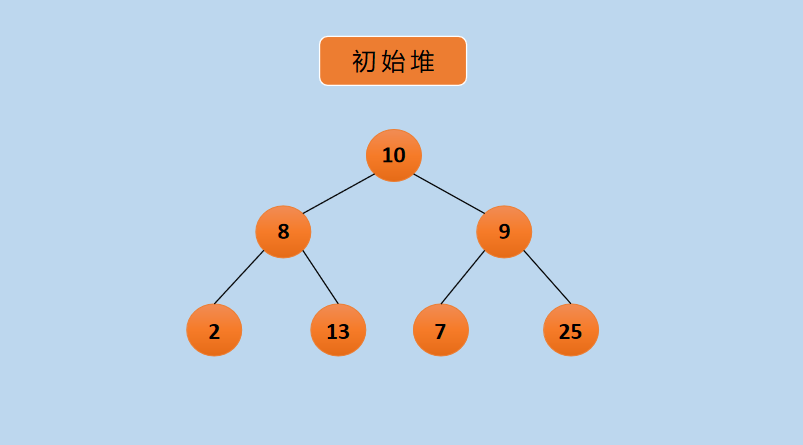 Graph Initial Heap
Graph Initial Heap
(2) Build a large top heap of elements to be sorted as follows:
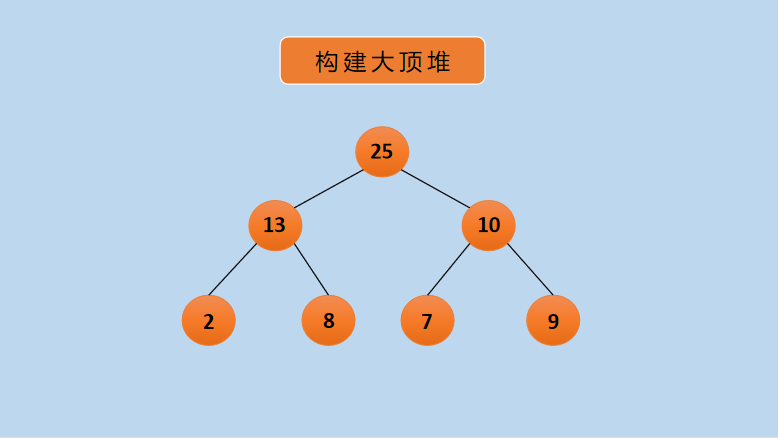 Graph Build Big Top Heap
Graph Build Big Top Heap
(3) Exchange node 9 with node 25 as follows:
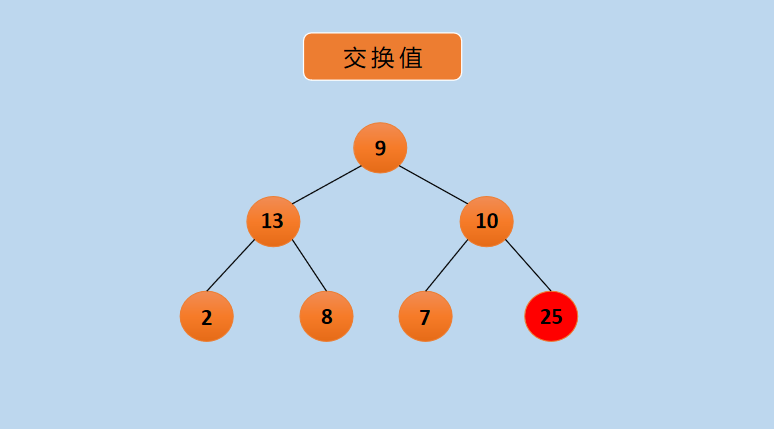 Graph Exchange Nodes 9 and 25
Graph Exchange Nodes 9 and 25
(4) Nodes marked red indicate that they are already in order and no longer participate in sorting. At this time, the heap does not satisfy the heap, and the heap is readjusted to the heap as follows:
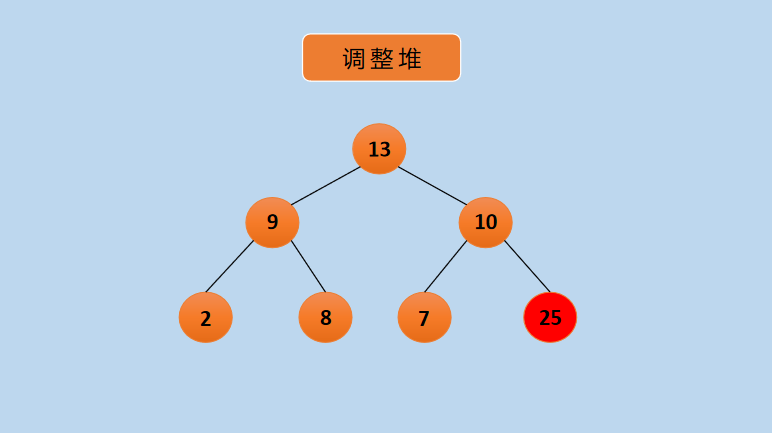 Graph readjusted to large top heap
Graph readjusted to large top heap
(5) Switch Node 13 with Node 7, and after that, the following:
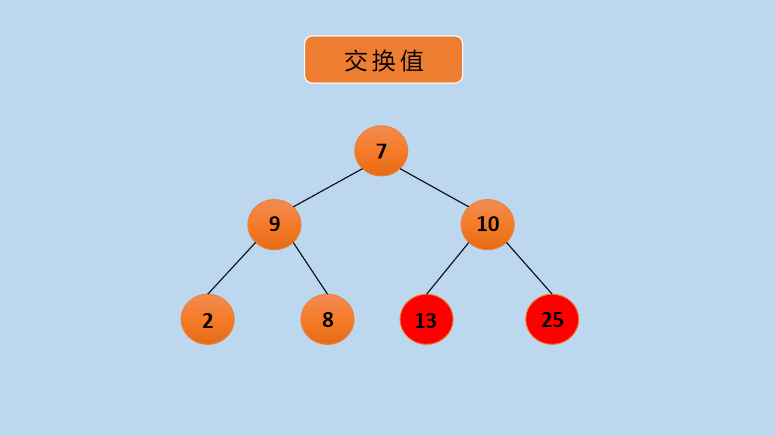 Diagram Exchange Nodes 7 and 13
Diagram Exchange Nodes 7 and 13
(6) After swapping, the heap is no longer a top heap at this time, and is readjusted to a top heap as follows:
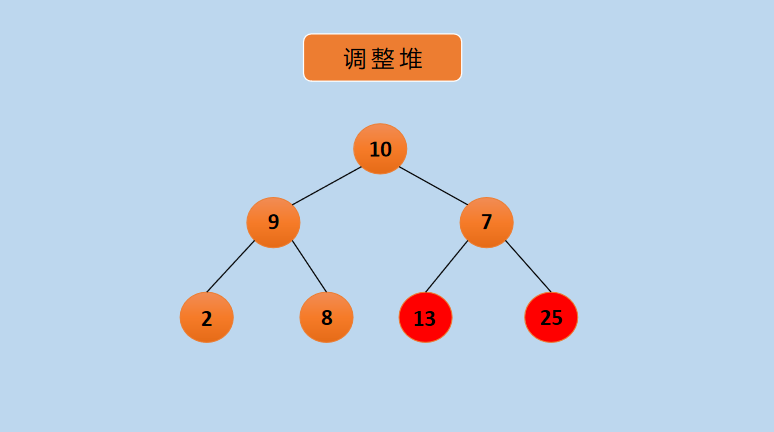 Graph Adjustment Heap
Graph Adjustment Heap
(7) Swap nodes 10 and 8 as follows:
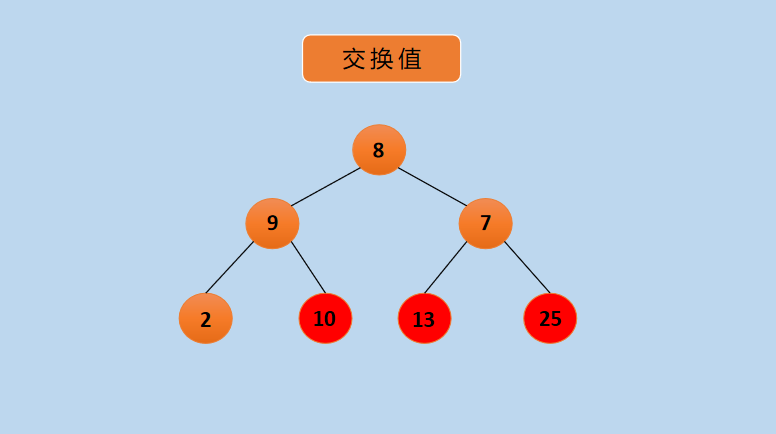 Graph Exchange Nodes 10 and 8
Graph Exchange Nodes 10 and 8
(8) At this point, the heap is no longer a large-top heap, and is readjusted to a large-top heap as follows:
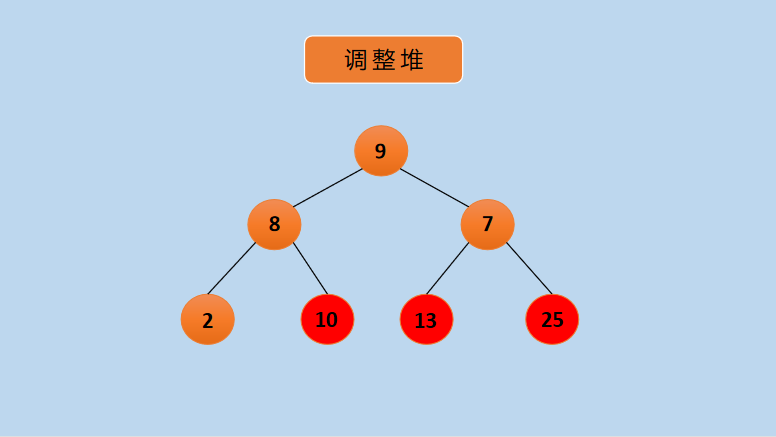 Graph Adjustment Heap
Graph Adjustment Heap
(9) Switch nodes 9 and 2, after which, as follows:
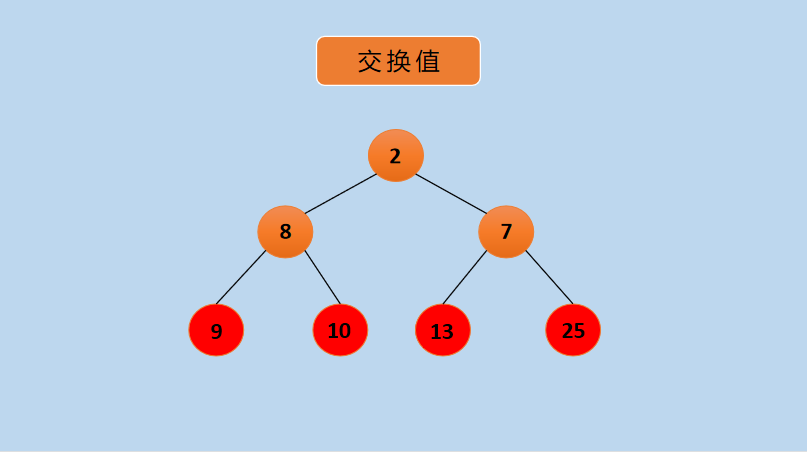 Diagram Exchange 9 and 2
Diagram Exchange 9 and 2
(10) Re-adjust the heap to a large top heap as follows:
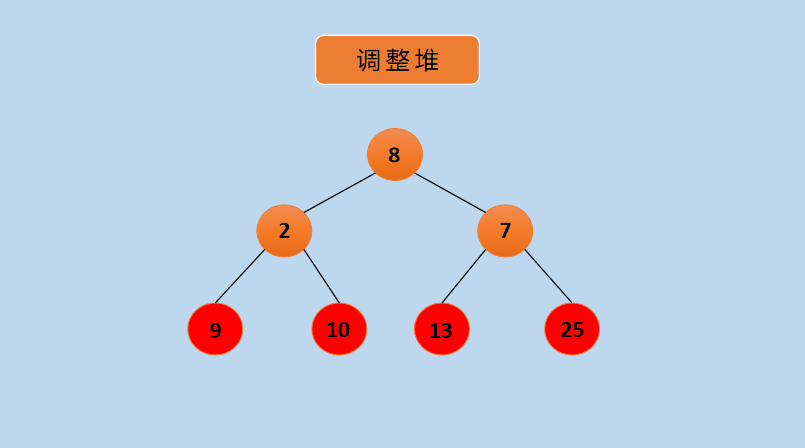 Graph Adjust Top Heap
Graph Adjust Top Heap
(11) Exchange values of 8 and 7 as follows:
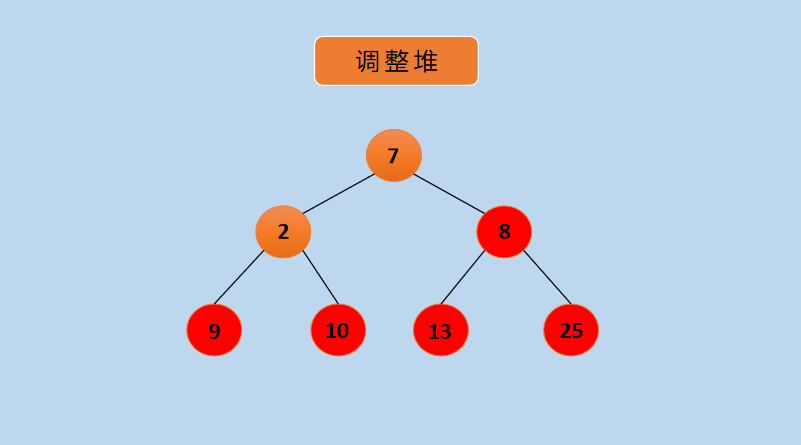 Diagram Exchange 8 and 7
Diagram Exchange 8 and 7
(12) Adjust the heap to a large-top heap, you can see that the current heap is already a large-top heap, and then swap nodes 2 and 7 as follows:
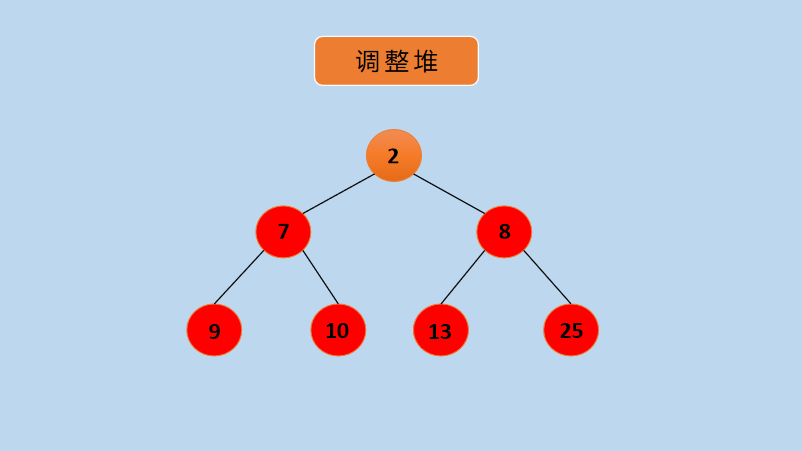 Diagram Exchange Nodes 7 and 2
Diagram Exchange Nodes 7 and 2
(13) At this point, the whole pair is incremental from top to bottom, from left to right, and is actually stored in the array as follows:
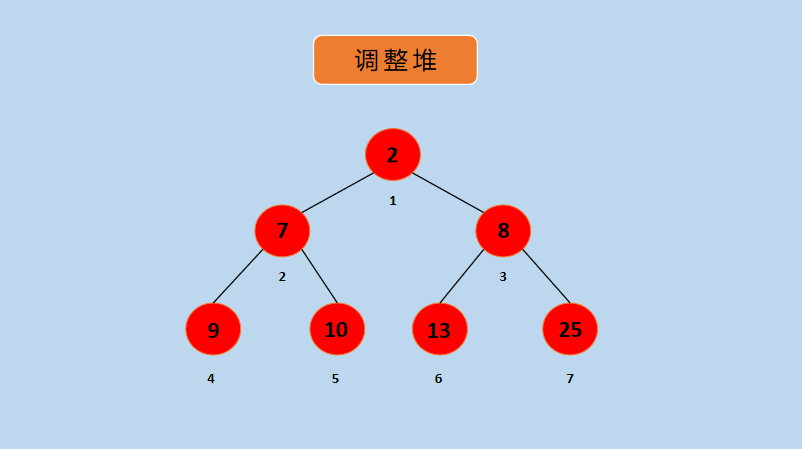 Position in the graph array
Position in the graph array
In the figure above, the number below the node represents the position of the node in the array and is generally stored starting with subscript 1, since this makes it easy to calculate the relationship between the parent and child nodes, as shown below:
(1) Subscript of left child node = Subscript of parent node* 2
(2) Subscript of right child node = Subscript of parent node* 2 + 1
✨ 2.4 code implementation
#include <iostream>
using namespace std;
//Adjust heap down, from idx node down
void adjustHeap(int a[], int idx, int Len){
while(idx*2+1 < Len) {
int temp = idx*2 + 1;
if(temp+1 < Len && a[temp+1] > a[temp]) {
temp++;
}
if(a[idx] < a[temp]) {
swap(a[idx], a[temp]);
idx = temp;
} else break;
}
}
/*
* Heap Sorting
* g[] : Array to Sort
* n : Number of elements
*/
void heapSort(int g[], int n){
//Build Top heap first
for(int i = (n-1)/2; i >= 0; --i){
adjustHeap(g, i, n);
}
//Sort, one element is ordered each time
for(int i = 0;i < n; ++i){
swap(g[0], g[n-i-1]);
adjustHeap(g, 0, n-i-1);
}
}
int main()
{
int n = 8;
int g[] = {5, 7, 9, 3, 1, 8, 6, 2};
heapSort(g, n); // Call Heap Sorting
for(int i = 0; i < n; ++i) {
cout<<g[i]<<" ";
}
cout<<endl;
return 0;
}During the heap sorting process, the emphasis is on adjusting the heap, and when a large-top heap is built (the first for loop in heapSort), each node is adjusted from bottom to top so that each node meets the conditions of the large-top heap.
When sorting formally, only the root node needs to be swapped each time, the heap can be readjusted, and only the new root node needs to be adjusted, because only the new root node does not satisfy the definition of the heap.
✨ 2.5 Heap Adjustment Principle
The most important thing in heap sorting is the adjustment of the heap. The following figure can be used as an example to illustrate, as follows:
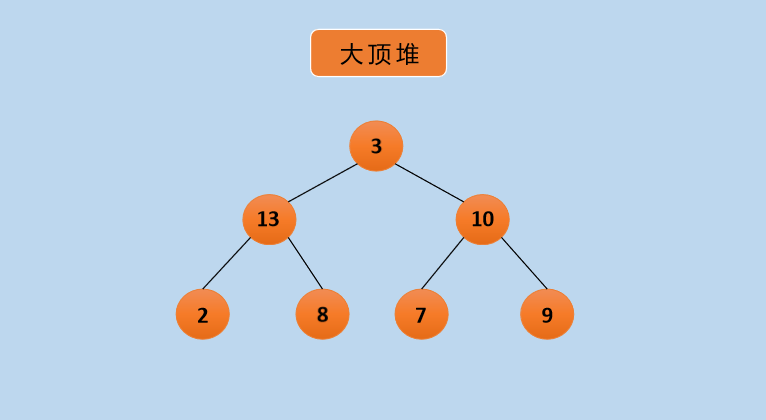 Figure 1 Heap adjustment diagram
Figure 1 Heap adjustment diagram
In the figure above, only 3 are not qualified, so adjust the next 3 nodes as follows:
 Heap Adjustment Kinematic Diagram
Heap Adjustment Kinematic Diagram
In the figure above, 3 exchanges with 13, then 8, and then becomes a large top heap.
🔶🔶🔶🔶🔶 I am a dividing line 🔶🔶🔶🔶🔶
🍓 3. Explanation of Examples
✨ 3.1 Find the k Big Element
Given the integer array nums and integer k, return the kth largest element in the array.
🚩 3.1.1 algorithm ideas
Sort the elements in the array nums by heap, since heap sorting can determine a maximum value at a time, only the k-th maximum value is required. If you use other sorting algorithms to sort all elements, this shows the advantage of heap sorting and does not require all sorting to find the kth largest element.
🚩 3.1.1 Code Implementation
#include <iostream>
#include <vector>
using namespace std;
class Solution {
public:
//Adjust heap down
void adjustHeap(vector<int>& nums, int idx, int Len) {
while(idx*2+1 < Len) {
int temp = idx*2 + 1;
if(temp + 1 < Len && nums[temp+1] > nums[temp]){
temp++;
}
if(nums[idx] < nums[temp]) {
swap(nums[idx], nums[temp]);
idx = temp;
} else break;
}
}
int findKthLargest(vector<int>& nums, int k) {
//Build Top heap first
int n = nums.size();
for(int i = (n-1)/2; i >= 0; --i){
adjustHeap(nums, i, n);
}
for(int i = 0; i < nums.size(); ++i) {
cout<<nums[i]<<" ";
}
cout<<endl;
//sort
for(int i = 0;i < k - 1; ++i){
swap(nums[0], nums[n-i-1]);
adjustHeap(nums, 0, n-i-1);
}
return nums[0];
}
};
int main()
{
int g[] = {5, 7, 9, 3, 1, 8, 6, 2};
vector<int> nums(g, g+8);
cout<<endl;
Solution obj;
int k;
while(cin>>k) {
cout<<"The k-th largest number is "<<obj.findKthLargest(nums, k)<<endl;
}
return 0;
}
✨ 3.2 Seek the Front Elements of high frequency k
You are given an array of integers nums and an integer k, and you are asked to return the elements that were K high before they appeared frequently. You can return the answers in any order.
🚩 3.2.1 algorithm ideas
This topic is similar to the first one, but you need to calculate the frequency of each integer, you can use map for statistics, and then you can use heap sorting to get the k-th largest.
🚩 3.2.2 Code implementation
#include <iostream>
#include <vector>
#include <map>
using namespace std;
class Solution {
public:
//Adjust heap down
void adjustHeap(vector<pair<int, int> >& nums, int idx, int Len) {
while(idx*2+1 < Len) {
int temp = idx*2 + 1;
if(temp + 1 < Len && nums[temp+1].second > nums[temp].second){
temp++;
}
if(nums[idx].second < nums[temp].second) {
swap(nums[idx], nums[temp]);
idx = temp;
} else break;
}
}
vector<int> topKFrequent(vector<int>& nums, int k) {
map<int, int>mp;
for(int i = 0; i < (int)nums.size(); ++i) {
mp[nums[i]]++;
}
vector<pair<int, int> >hep;
map<int, int>::iterator it;
for(it = mp.begin(); it != mp.end(); ++it) {
hep.push_back(pair<int, int>(it->first, it->second));
}
//Build Top heap first
int n = hep.size();
for(int i = (n-1)/2; i >= 0; --i){
adjustHeap(hep, i, n);
}
//sort
vector<int> ans;
for(int i = 0;i < k - 1; ++i){
ans.push_back(hep[0].first);
swap(hep[0], hep[n-i-1]);
adjustHeap(hep, 0, n-i-1);
}
ans.push_back(hep[0].first);
return ans;
}
};
int main()
{
int g[] = {1, 2, 2, 1, 3, 8, 8, 1};
vector<int> nums(g, g+8);
cout<<endl;
Solution obj;
int k;
while(cin>>k) {
vector<int> ans = obj.topKFrequent(nums, k);
for(int i = 0; i < ans.size(); ++i) {
cout<<ans[i]<<" ";
}
cout<<endl;
}
return 0;
}
🔶🔶🔶🔶🔶 I am a dividing line 🔶🔶🔶🔶🔶
🍓 4. Summary
Heap sorting is often used on the K-th largest because the root element must be the largest/smallest element for each heap adjustment.

Welcome to the following 👇👇👇 Public Number 👇👇👇, Get more benefits when you come 🤞 (heart to heart)!