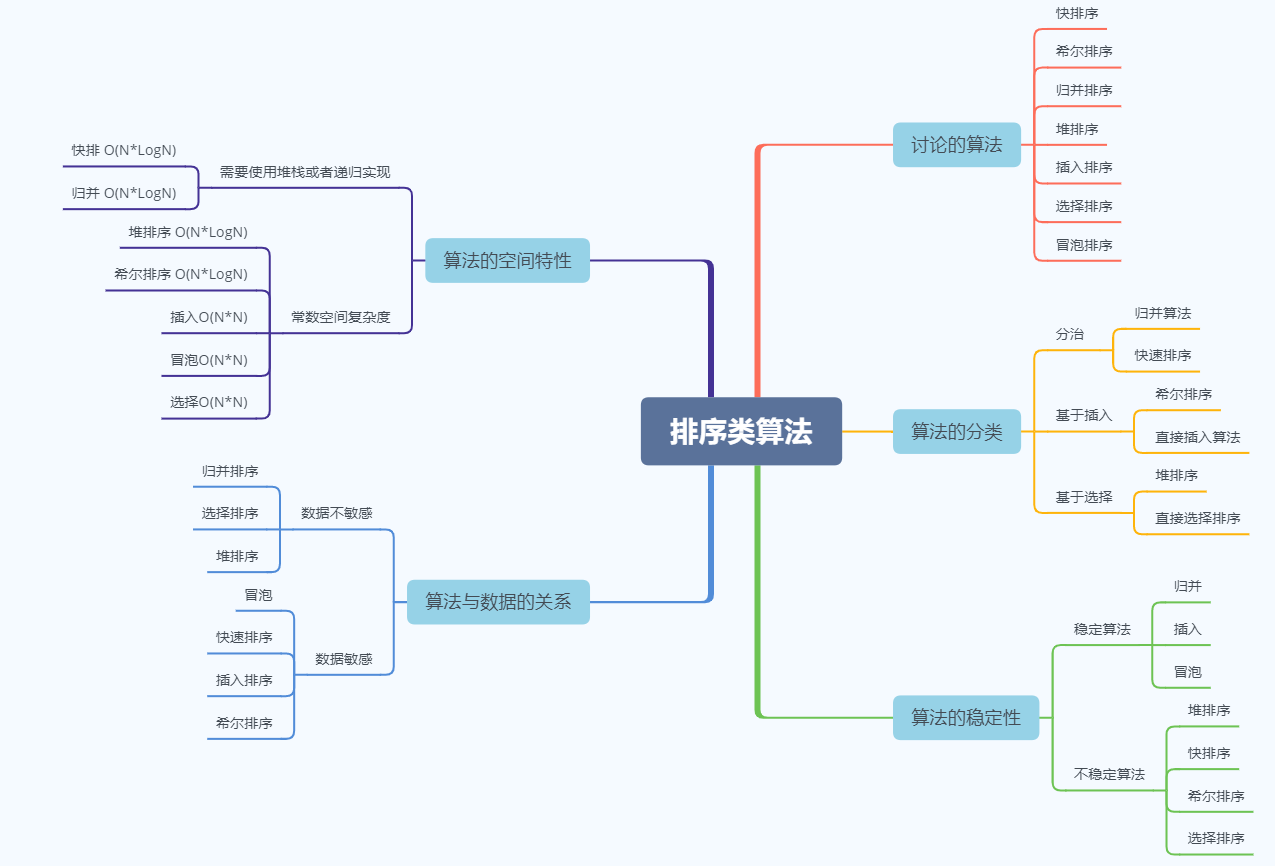
Overview of learning contents in this section

Sorting concept

• Sorting is the operation of arranging a string of records incrementally or decrementally according to the size of one or some keywords.
• In the usual context, if sorting is mentioned, it usually refers to ascending order (non descending order).
• Sorting in the usual sense refers to in place sort

stability

If the sorting algorithm can ensure that the relative position of two equal data does not change after sorting, we call the algorithm a stable sorting algorithm.

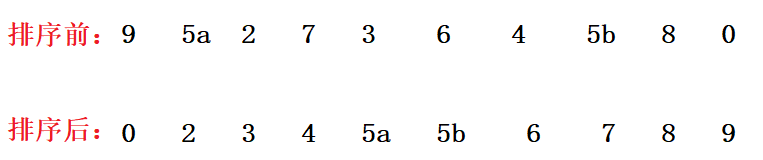
1, Insert sort

Basic principle and process of insertion sorting

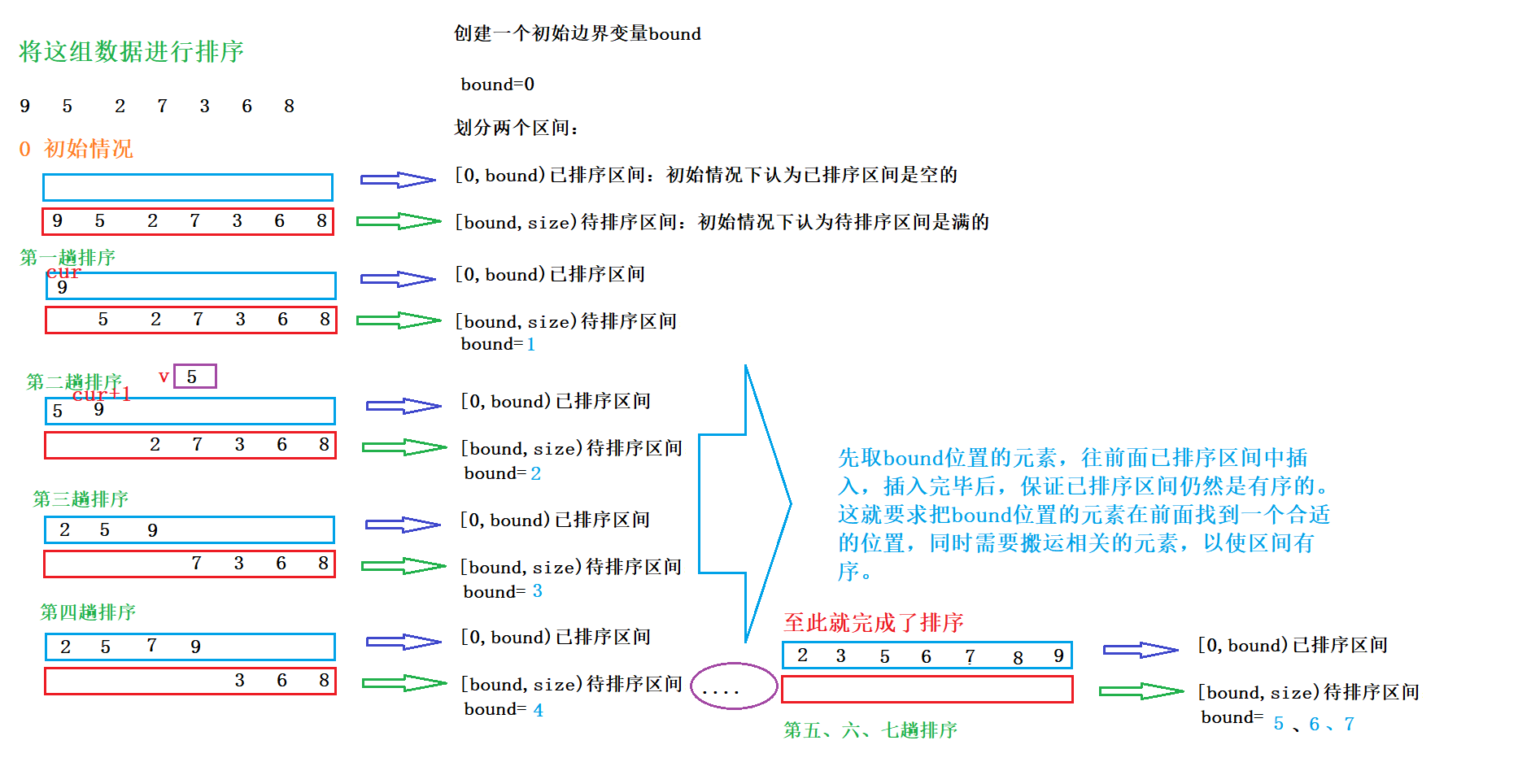
The whole interval is divided into

1. Ordered interval (sorted interval)
2. Unordered interval (to be sorted interval)
   Select the first element of the unordered interval each time and insert it at the appropriate position in the ordered interval

Insert sort is very similar to the sequential table insert learned earlier. If this group of data is sorted: 9 5 2 7 3 6 8

Train of thought analysis: or drawing

Implementation of insert sort

Code implementation:

package java2021_1013;

import java.util.Arrays;

/**
 * Created by Sun
 * Description:Insert sort
 * User:Administrator
 * Date:2021-10-19
 * Time:10:31
 */
public class TestSort {
    //Sort in ascending order
    public static void insertSort(int[] array){
        //Two sections are divided by bound
        //[0,bound) sorted interval
        //[bound,size) range to be sorted
        //Here, the bound starts with 1
        for(int bound=1;bound < array.length;bound++){
            int v=array[bound];  //Take out the value of the bound position and save it in a separate variable v
            int cur=bound-1;//cur represents the subscript of the last element of the sorted interval. Through this subscript, comparison and handling operations are performed
            for(;cur>=0;cur--){//cur moves forward from the back. cur starts from bound-1. If it is always greater than or equal to 0, then--
                if(array[cur]>v){//Compare and transport from the back to the front to judge which is the greater of the subscript of cur position and the value of v
                    array[cur+1]=array[cur];//If cur is large, carry it, that is, take one step backward, and then a handling is completed
                }else{
                    break;//If v is large, it means that a suitable position has been found and there is no need to carry it
                }
            }
            array[cur+1]=v;//Assign the value stored in a separate variable v to the corresponding position,
        }
    }
//Test sorting effect
    public static void main(String[] args) {
        int[] arr={9,5,2,7,3,6,8};
        insertSort(arr);
        System.out.println(Arrays.toString(arr));
    }
}
Print results:
   [2, 3, 5, 6, 7, 8, 9]

Performance analysis of insert sort

Time complexity of insertion sorting: there are two loops in the code. The first loop circulates length times, that is, it circulates as many times as there are many elements, that is, O(N), and each large loop has to cycle several times, that is, the second loop may also cycle N times, that is, O(N), so its overall complexity is O(N^2).

When the data is ordered, its time complexity is optimal, which is O(N);

The average time complexity is O(N^2);

The worst time complexity is O(N^2) when the data is in reverse order.

Space complexity of insertion sort: look at the number of temporary variables created in the above code, namely bound, v and cur. You can know that no matter how many elements in the array, they are always these three temporary variables, so the additional space and array currently occupied (i.e. problem scale) The space complexity is O(1) because it does not introduce too much additional space

Stability: the current insertion sort is a stable sort.

What is stable?: if the values of two elements in an array are the same, what is the relative order between the two elements? If the order can be guaranteed to be consistent with the original order after sorting, it is called stable sorting, otherwise it is unstable sorting.

For example:

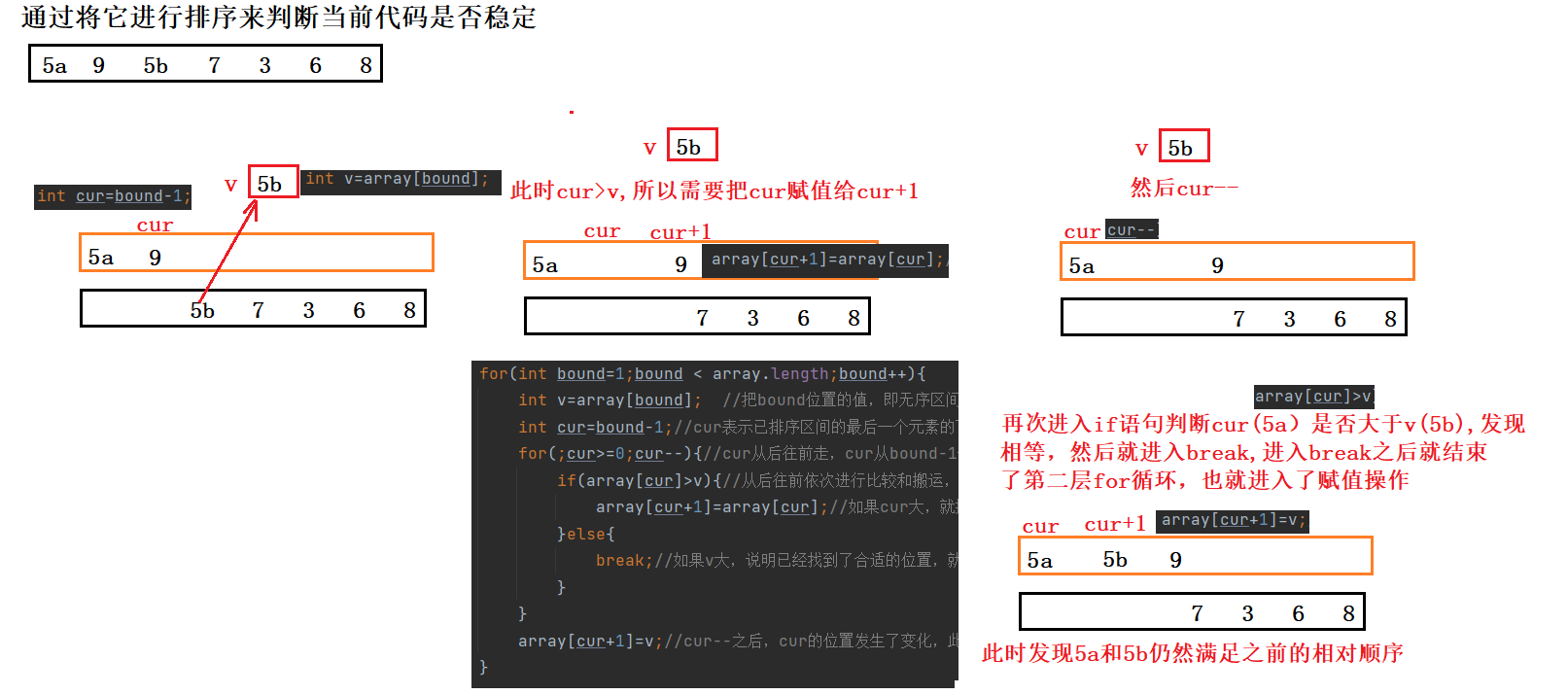
5a is in the first place, 5b is in the second place, and 5a is still in front of 5B after sorting, which still conforms to the original relative order. At this time, it shows that it is a stable sorting.

Two important characteristics of insertion sort

1. When there are few sorting interval elements, the sorting efficiency is very high;

2. When the whole array is close to order, the sorting efficiency is also high, that is, the closer the initial data is to order, the higher the time efficiency.

Half insert sort (not mentioned)

2, Hill sort

Basic principle and process of Hill sort

Hill sort is equivalent to the advanced version of insertion sort. It groups the original first, performs insertion sort (interpolation) for each group, gradually reduces the number of groups, and finally the whole array is close to order.

If you don't know the process of hill sorting, please be patient and read it step by step. After reading it, you will feel that you still understand it!

Let's take an example and draw a picture to understand the hill sorting process:

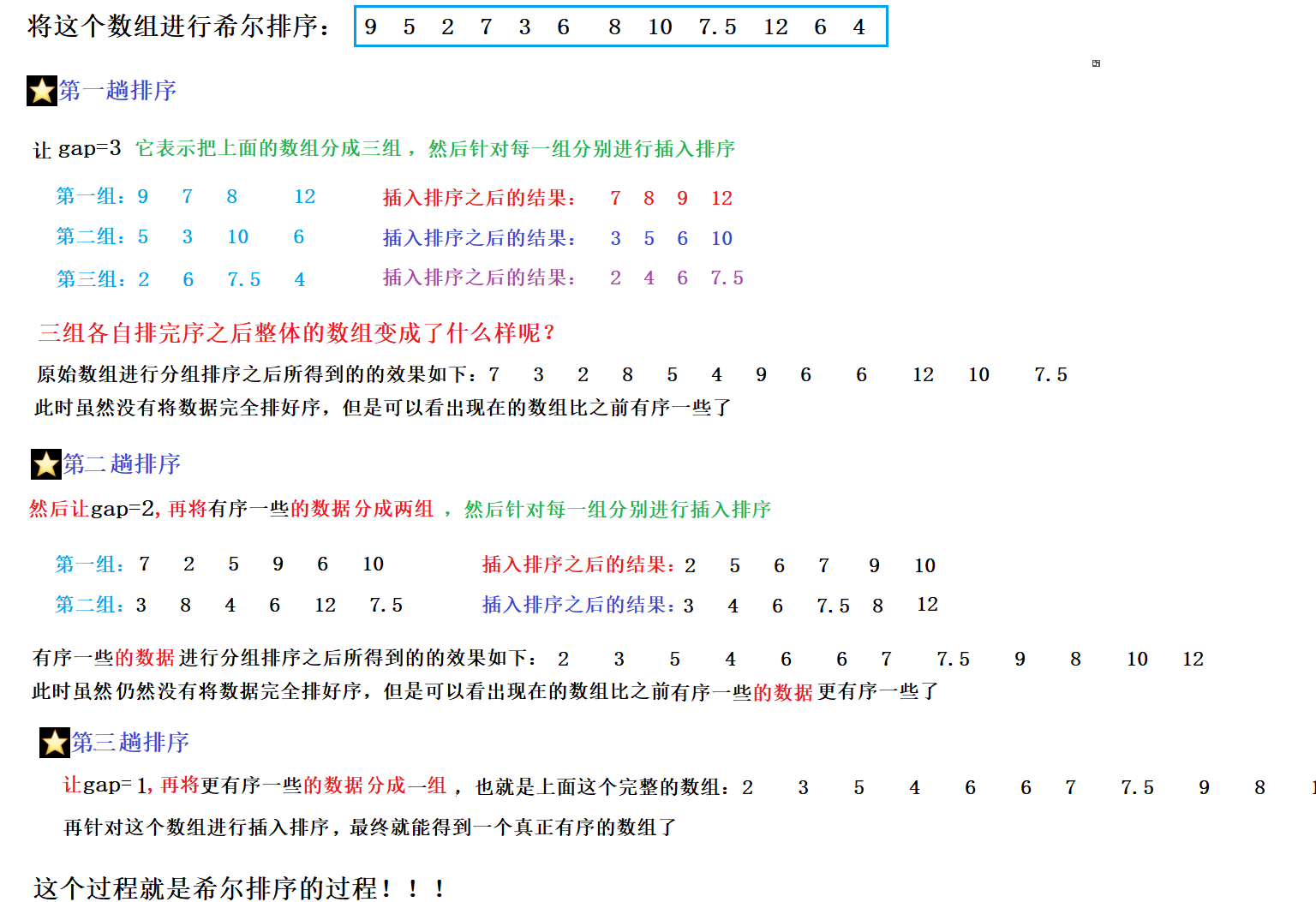
Question: why does Hill rank like this?

Look at the two important features of the insertion written above. Forget it, write it again

Two important characteristics of insertion sort

1. When there are few sorting interval elements, the sorting efficiency is very high; * * Hill sorting divides a group of arrays with a lot of data into n groups, which reduces the elements of the sorting interval and improves the efficiency;

2. When the whole array is close to order, the sorting efficiency is also very high, that is, the closer the initial data is to order, the higher the time efficiency. Hill sorting finally makes the whole array close to order, which improves the efficiency while performing insertion sorting.

Note: generally, gap cannot be set according to 3, 2 and 1 when Hill sorting is implemented. The above example is only set for analysis. The common gap values are: size, size/2, size/4... 1

Implementation of hill sorting

Code implementation:

 //II. Hill ranking
    public static void shellSort(int[] array){
        int gap= array.length/2;//Initially, let gap group from length/2
        while(gap>1){//If it is greater than 1, grouping and arrangement is required
            //Construct an insertion method to create a grouped insertion method
            insertSortGap(array,gap);
            gap=gap/2;//Divide gap by 2 each time,
        }
        //Until gap is 1, arrange again (insert sort) according to gap is 1
        insertSortGap(array,1);//When gap is 1

    }
    private static void insertSortGap(int[] array, int gap) {
        //Write an insertion sort in this insertion method
        //Two sections are divided by bound
        //[0,bound) sorted interval
        //[bound,size) range to be sorted
        //Here, the bound starts from gap, and the gap is a few, which means that the bound starts from a few
        for(int bound=gap;bound < array.length;bound++){
            //The meaning of this cycle is:
            /*The first and second elements of the first group are processed first
            * Reprocess the first and second elements of the second group
            * Reprocess the first and second elements of the third group
            * Reprocess the second and third elements of the first group
            * .....Until all groups are processed*/
            int v=array[bound];  //That is, the first number of the unordered interval, first take it out and save it in a separate variable v,
            int cur=bound-gap;//This operation is to find the previous element in the same group
            for(;cur>=0;cur-=gap){//cur-=gap means to find adjacent elements in the same group, and the subscript difference of elements in the same group is gap
                if(array[cur]>=v){//Compare and transport from the back to the front to judge which is the greater of the subscript of cur position and the value of v
                    array[cur+gap]=array[cur];//If cur is large, carry it, that is, take one step backward, and then a handling is completed
                }else{
                    break;//If v is large, it means that a suitable position has been found and there is no need to carry it
                }
            }
            array[cur+gap]=v;//Cur -- after that, the position of cur changes. At this time, the value saved in a separate variable v is assigned to the corresponding position, that is, the position of cur+1
        }
    }
 //Test sorting effect
    public static void main(String[] args) {
        int[] arr={9,5,2,7,3,6,8,10,7,12,6,4};
        shellSort(arr);
        System.out.println(Arrays.toString(arr));
    }
}
Print results:
[2, 3, 4, 5, 6, 6, 7, 7, 8, 9, 10, 12]            

Performance analysis of insert sort

The time complexity of Hill sort: theoretically, it can reach O(N^1.3). If the gap sequence is set according to the value of size, size/2, size/4... 1, its time complexity is still O(N^2)

When the data is ordered, its time complexity is optimal, which is O(N);

The average time complexity is O(N^1.3);

The worst time complexity is O(N^2), which is difficult to construct.

Spatial complexity of Hill sort: there is only one gap variable more than insert sort, and there is still no extra space, so the spatial complexity is O(1)

Stability of hill sorting: unstable, because the same value may be divided into different groups during grouping, so the relative order cannot be guaranteed, so it is unstable.

3, Select sort

Basic principle and process of selection sorting

Principle: find a minimum value from the interval to be sorted each time and put it at the end of the sorted interval.

Based on the idea of challenge arena, compare and exchange the current element with the challenge master element, find the minimum value from the array each time, and then put the minimum value in the appropriate position.

Take a specific example to understand the basic idea and process, as shown in the following figure:

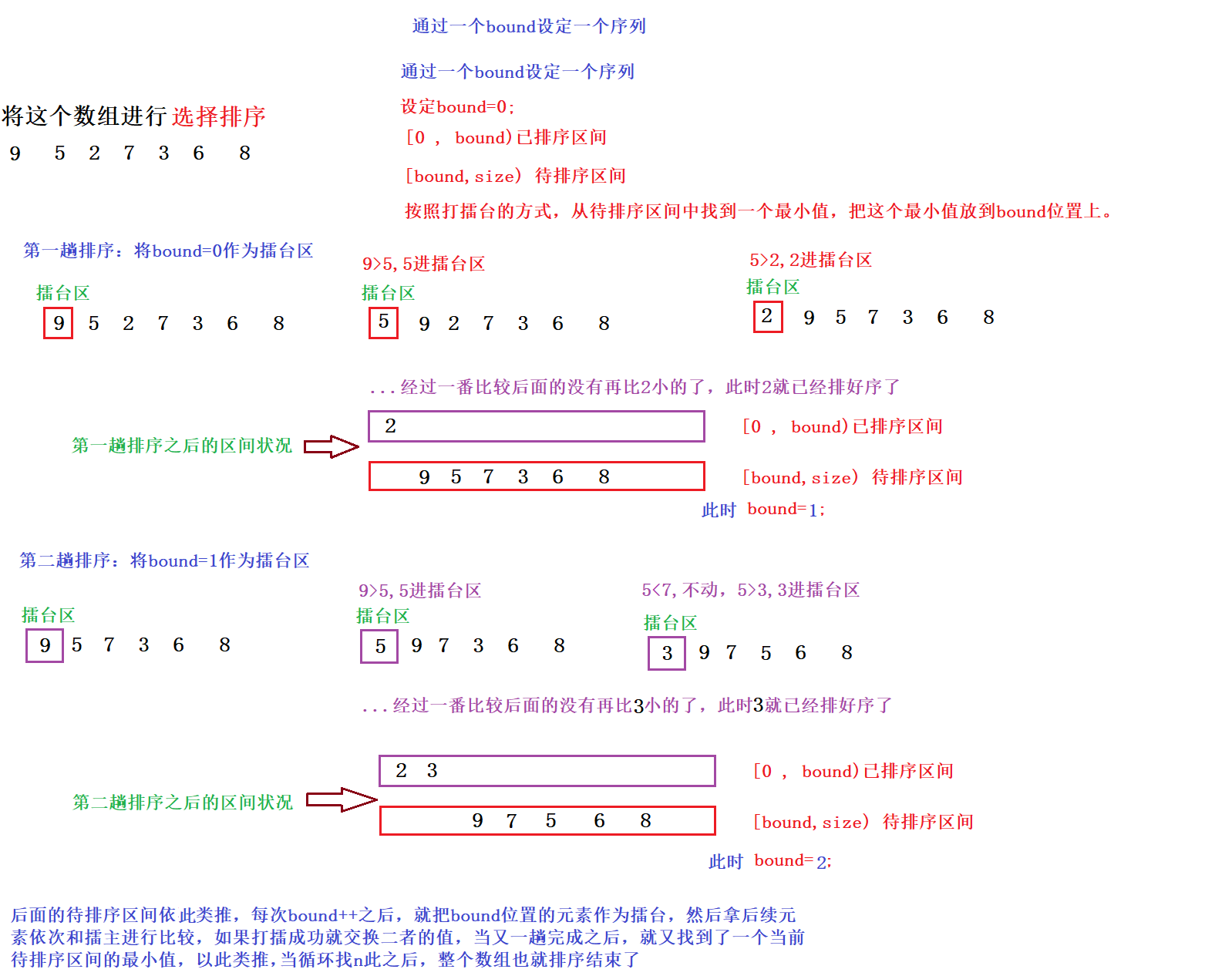
Implementation of selective sorting

code implementation

 public static void selectSort(int[] array){
        for(int bound=0;bound<array.length;bound++){
            //Take the element at the bound position as the challenger, take out the element from the interval to be sorted and compare it with the challenger. If the challenge is successful, exchange it with the challenger
            for(int cur=bound+1;cur< array.length;cur++){
                if(array[cur]<array[bound]){//If the current value is less than the challenge master
                    //Successful challenge, exchange
                    int tmp=array[cur];
                    array[cur]=array[bound];
                    array[bound]=tmp;
                }
            }
        }

    }
 //Test sorting effect
    public static void main(String[] args) {
        int[] arr={9,5,2,7,3,6,8};
        selectSort(arr);
        System.out.println(Arrays.toString(arr));
    }
}

Print results:
 [2, 3, 5, 6, 7, 8, 9]

Performance analysis of selective sorting

Select the time complexity of sorting: the outer layer circulates N times and the inner layer circulates N times, so the time complexity is O(N^2);

Spatial complexity of sorting: the number of temporary variables is fixed and has nothing to do with the array size, so the spatial complexity is O(1);

Select the stability of sorting: unstable sorting.

For example: int [] a = {9, 2, 5A, 7, 4, 3, 6, 5b};

This situation cannot be identified during the exchange, and it is guaranteed that 5a is still ahead of 5b

4, Bidirectional selection sorting (understand)

5, Heap sort

Basic principle and process of heap sorting

• The basic principle is also selective sorting, but instead of using traversal to find the maximum number of unordered intervals, it selects the maximum number of unordered intervals through the heap.
• Find a minimum value from the interval to be sorted each time and put it at the end of the sorted interval;
• Or find a maximum value from the interval to be sorted each time and put it at the front of the sorted interval (it is recommended to find the maximum value (build a pile)

Heap sorting style: in ascending order, build a lot; Small piles shall be built in descending order;

Scheme 1: first build the array into a small heap. At this time, the top element of the heap is the minimum value. Take the minimum value and put it into another array. Cycle to take the top element of the heap and insert it into the new array. In fact, this is equivalent to a selection sort of upgraded version. This is a solution, but this solution has a small defect, because it needs additional * * O(N) * * space to put the minimum value into another array. This way of thinking is relatively simple, but there is a little more space.

Scheme 2: first build the array into a large pile, exchange the top element of the heap with the last element of the array, delete the last element, and then adjust downward from the top of the heap. This method does not need to waste additional space and toss on the current array, so its space complexity is O(1)

Go through the style process of scheme II by drawing: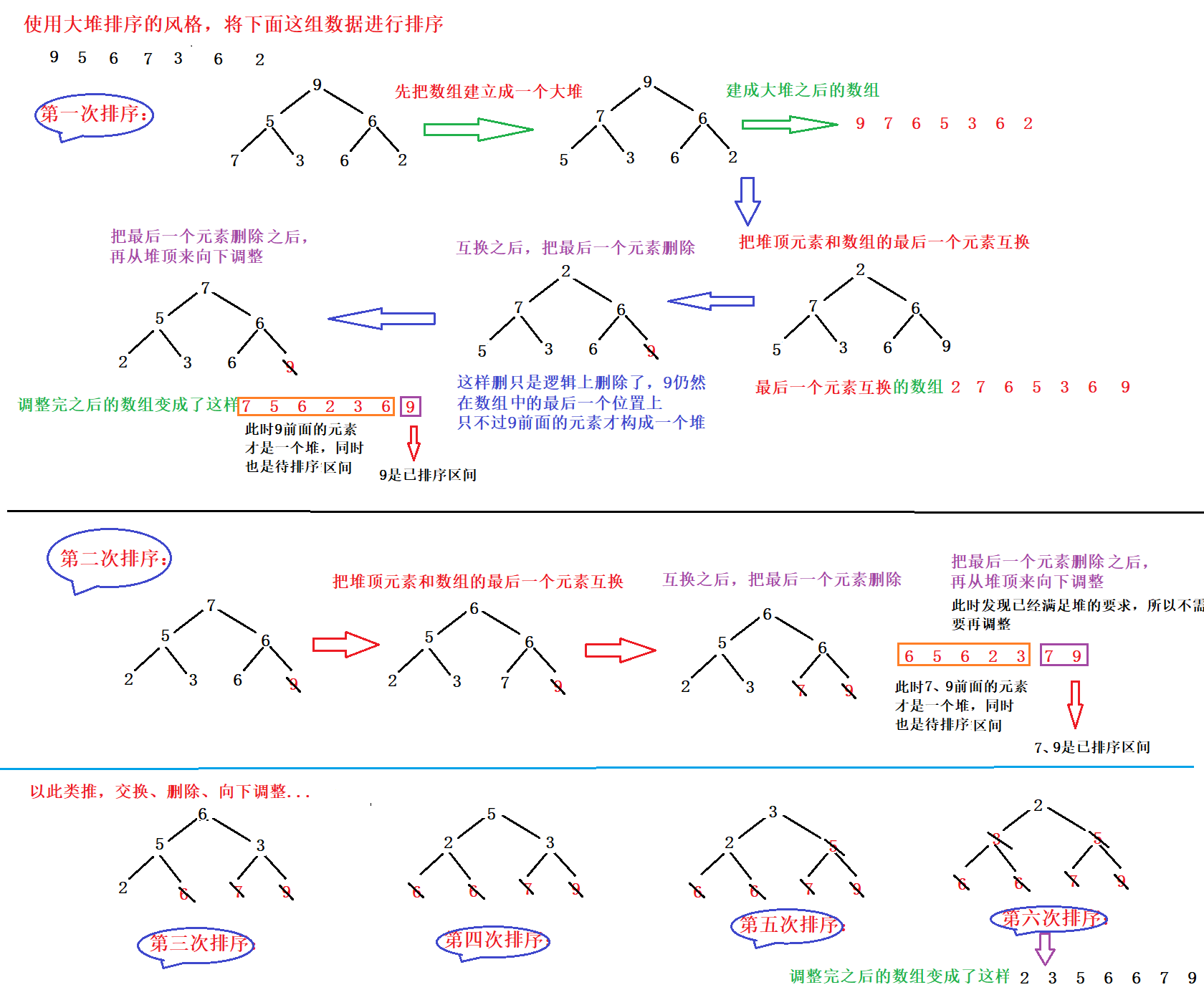

Implementation of heap sorting

Code implementation:

    //IV. heap sorting
    private static  void  swap(int[] array,int i,int j){
        //Exchange i and j
        int tmp=array[i];
        array[i]=array[j];
        array[j]=tmp;
    }
    public static void heapSort(int[] array){
        //Build the heap first
        //Write a separate heap building method
        creatHeap(array);
        //The loop switches the top elements to the last and adjusts the heap
        for(int i=0;i<array.length-1;i++){//When there is only one element left in the heap, it must be orderly and there is no need to recycle, so it is enough to cycle length-1 times
            //By swapping the top element of the heap with the last element of the heap, you can write a separate swap method
            swap(array,0,array.length-1-i);//Call swap
            //The number of elements in the heap is equivalent to array.length-i. if I cycles more than once, there will be one less element in the heap
            //The subscript of the last element of the heap is array.length-i-1;

            //After the exchange is completed, the last element is deleted from the heap, and the length of the heap is further reduced by array.length-i-1
            //In array
            //[0,array.length-i-1) is the interval to be sorted
            //[array.length-i-1,array.length) is the sorting interval

            //Downward adjustment
            //Pay attention to the boundary conditions in this code. See whether it is - 1, no reduction or + 1. It is best to substitute it into the numerical value for verification. For example, when i=0, see whether the logic is reasonable
            shiftDown(array,array.length-i-1,0);
            //Adjust from subscript 0 to array.length-i-1, and pay attention to the boundary conditions
        }
    }

    private static void creatHeap(int[] array) {
    //Heap building: start from the last non leaf node, cycle forward and adjust downward in turn
        for(int i=(array.length-1-1)/2;i>=0;i--){
            //length-1 is the subscript of the last node, and then - 1 / 2 is the parent node of the last node
            shiftDown(array,array.length,i);
        }
    }

    private static void shiftDown(int[] array, int heapLength, int index) {
    //This is an ascending sort. A lot is created. For a lot, you need to find the larger value in the left and right subtrees and compare it with the root node
    int parent = index;
    int child=2 * parent+1;
    while(child < heapLength){
        if(child+1 < heapLength && array[child+1] > array[child]){
            child=child+1;
        }
        //The end of the condition means that child is already the subscript of the larger value of the left and right subtrees
        if(array[child] > array[parent]){
            //Two elements need to be exchanged
            swap(array,child,parent);
        }else{
            break;
        }
        parent=child;
        child=2 * parent +1;
    }
   }
    //Test sorting effect
    public static void main(String[] args) {
        //Test heap sorting
        int[] arr={9,5,6,7,3,6,2};
        heapSort(arr);
        System.out.println(Arrays.toString(arr));
    }
}

Print results:
 [2, 3, 5, 6, 6, 7, 9]

Performance analysis of heap sorting

The time complexity of heap sorting: heap building: (O(N)), loop: N times, the shifDown in the loop is adjusted downward: logN, so O(N)+O(N*logN)=O(N *logN), logN can be regarded as O(1);

So o (n * logn) < o (n ^ 2), but o (n * logn) > O (n ^ 1.3)

Spatial complexity of heap sorting: O(1)

Stability of heap sorting: unstable sorting;

6, Bubble sorting

Basic principle and process of bubble sorting

Bubble sorting: its core goal is similar to heap sorting / selection sorting. Each time, a minimum or maximum value is found from the interval to be sorted and placed in the appropriate position (the minimum value is placed at the end of the sorted interval and the maximum value is placed at the front of the sorted interval). It is found by comparing and exchanging adjacent elements.

Take ascending sorting as an example: drawing analysis

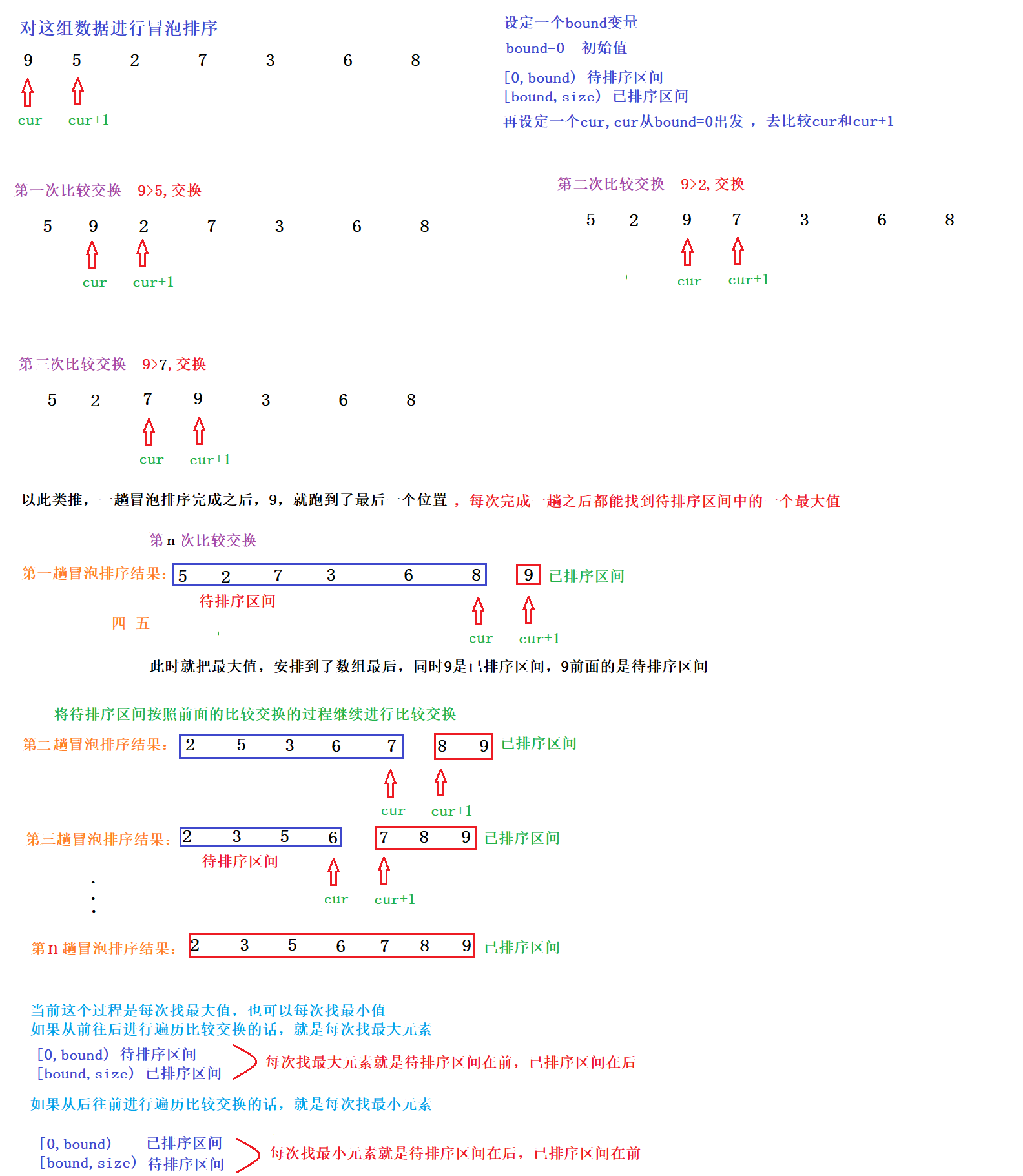
Implementation of bubble sorting

Code implementation: the process in the figure above takes the ascending order (finding the maximum value) as an example, and the code here takes the descending order (finding the minimum value) as an example.

    public static void bubbleSort(int[] array){
        //Sort according to the method of finding the smallest each time (compare and exchange from back to front)
        //[0,bound) sorted interval
        //[bound, size) range to be sorted
        for(int bound = 0;bound < array.length; bound++){
            for(int cur = array.length-1;cur>bound; cur--){
                //Why cur > bound instead of > =? You can bring in a number to verify. When bound is 0, if > =, cur is also 0 and cur-1=-1, the subscript is out of bounds
                if(array[cur-1] > array[cur]){//Why is cur-1 here instead of cur+1? Cur-1 is because the initial value of cur is array.length-1. If you take the element of cur+1 subscript, it is out of bounds.
                    swap(array,cur-1,cur);
                }
            }
        }
    }

Print results:
[2, 3, 5, 6, 7, 8, 9]

Performance analysis of bubble sorting

The time complexity of bubble sorting: the first cycle is O(N), and the second cycle is O(N), so the time complexity is O(N^2)

The space complexity of bubble sorting: O(1)

Stability of bubble sorting: stable sorting

7, Quick sort (important)

Basic principle and process of quick sort

Basic idea: rely on recursion. Recursion is about the left and right intervals.

1. Now find a benchmark value in the interval to be sorted (it is common to take the first element or the last element of the interval as the benchmark value).

2. Taking the benchmark value as the center, the whole interval is divided into three parts: the elements in the left part are less than or equal to the benchmark value, the elements in the right part are greater than or equal to the benchmark value, and the middle part is the benchmark value;

3. Then, for the interval sorted on the left and the interval sorted on the right, perform further recursion and repeat the sorting process just now. After finishing the left and right sorting, the sorting is also arranged.

For example, given a group of numbers, this group of numbers can be quickly sorted.

9 5 2 7 3 6 8 10 -1 4

Drawing analysis sorting process: take the right element as the benchmark value as an example

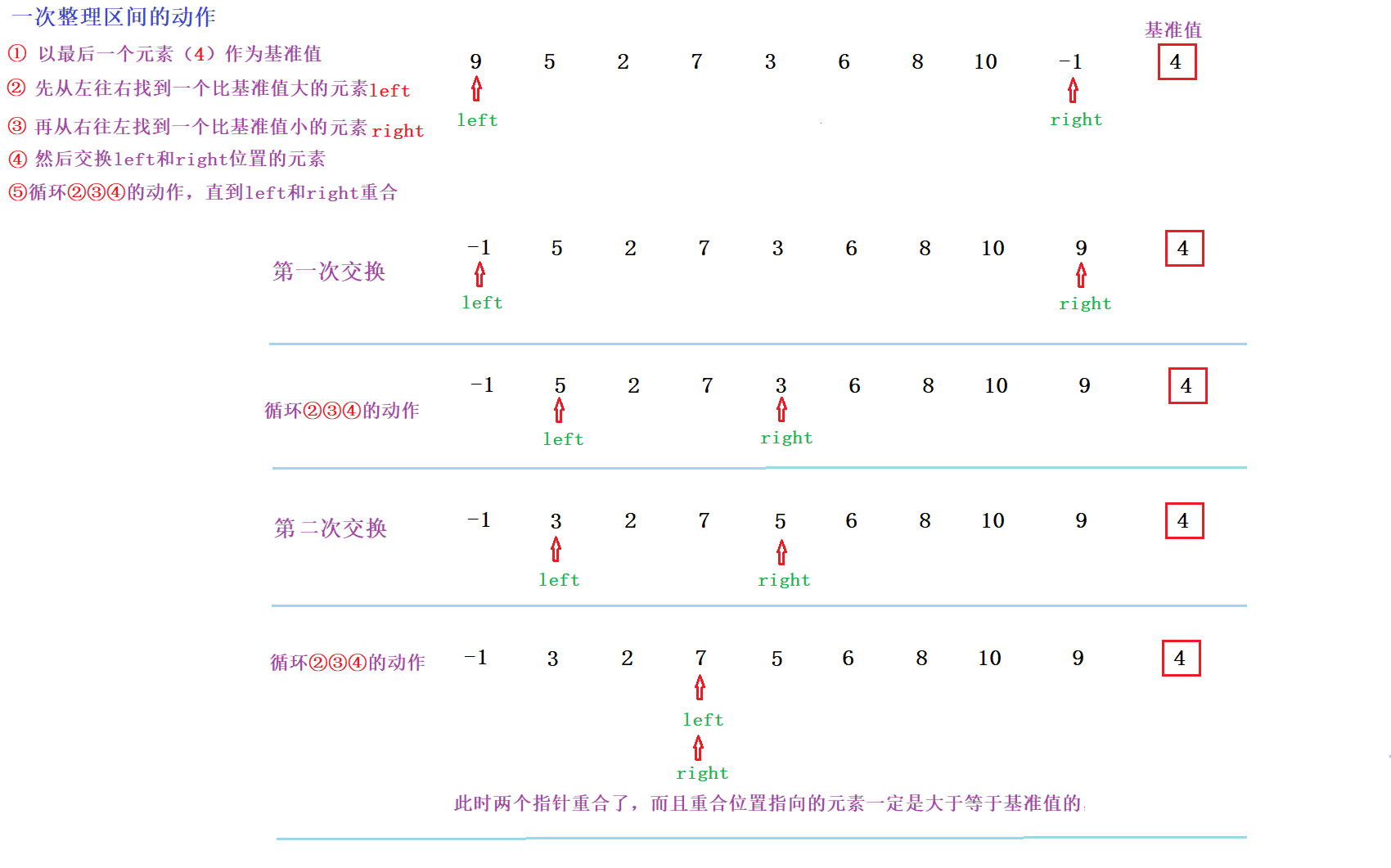
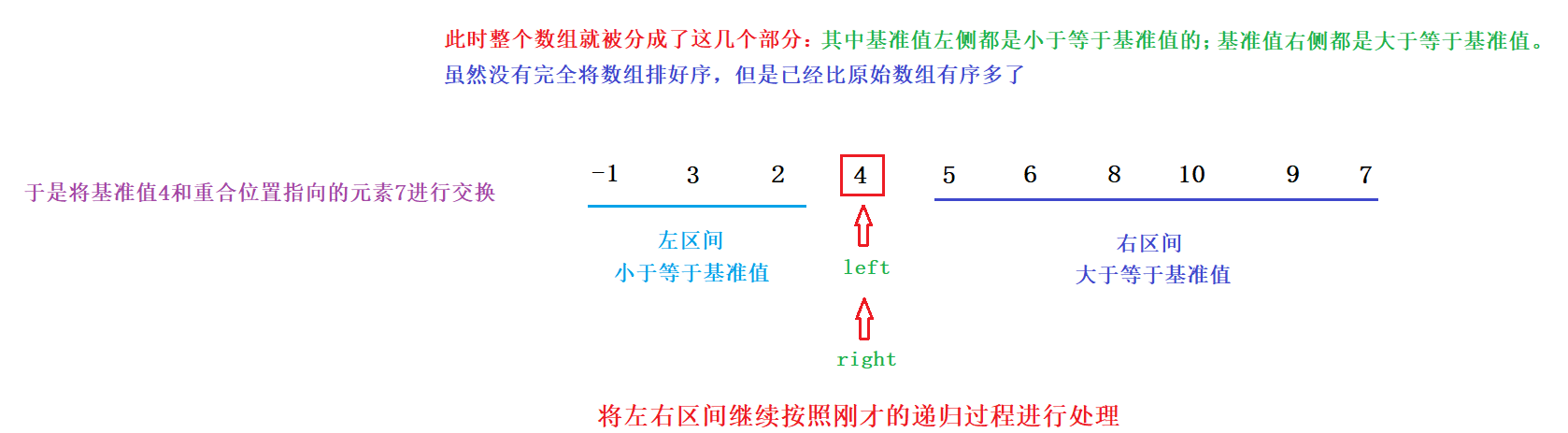
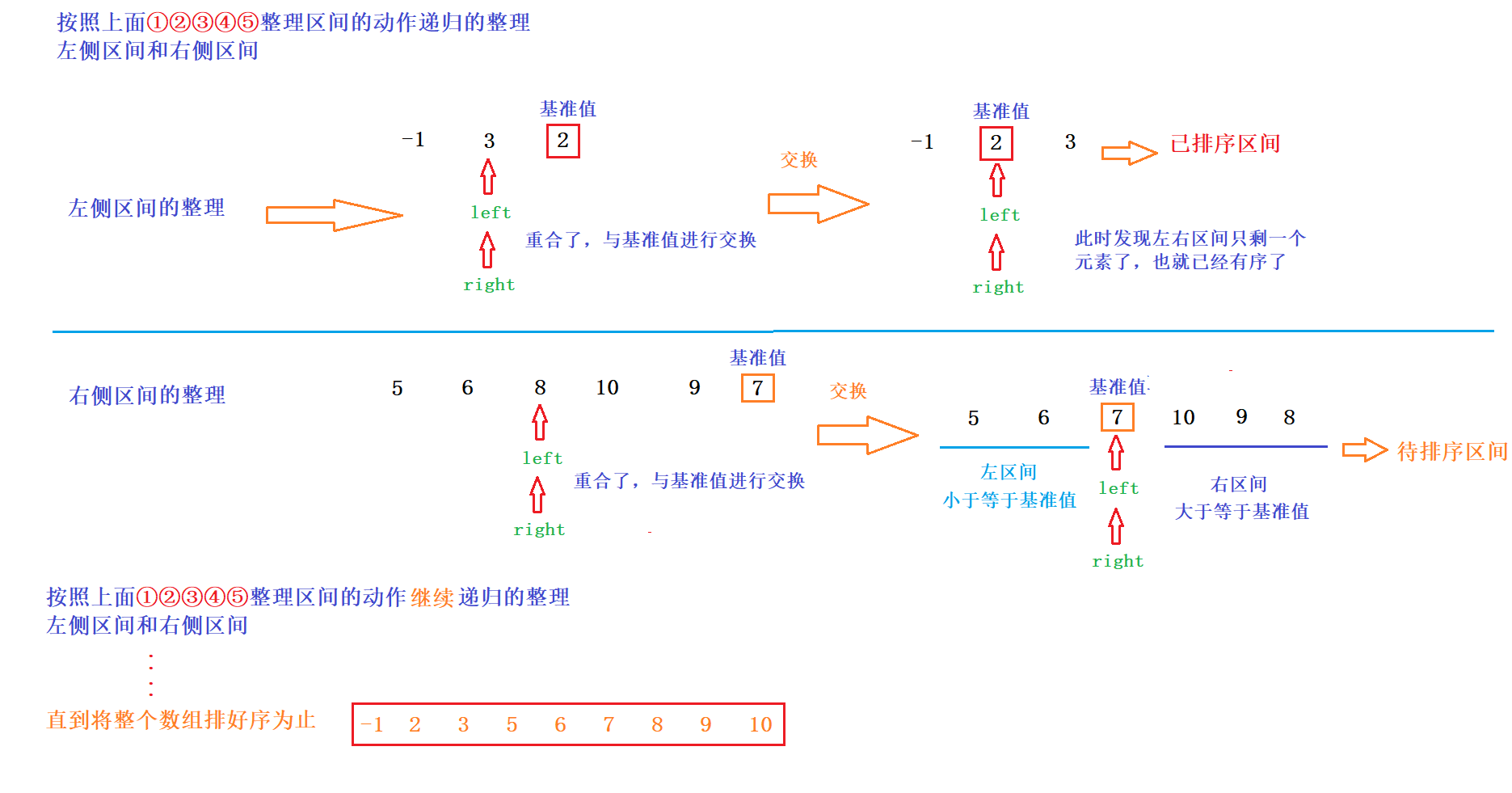
Note: the relationship between quick sort efficiency and benchmark value?

The efficiency of quick sorting is closely related to the quality of the benchmark value. The benchmark value is an element close to the median of the array. The divided left and right intervals are relatively balanced. At this time, the efficiency is relatively high. If the currently obtained benchmark value is the maximum or minimum value, the divided intervals are unbalanced and the efficiency is low.

If the array is in reverse order, the fast sort will become slow sort. At this time, the fast sort efficiency is very low, and the time complexity is O(N^2), which is also the worst time complexity;

If the exchange is relatively average (as in the example above), the average time complexity is O(NlogN);

There is a difference between taking the right element as the reference value and taking the left element as the reference value

Take the rightmost element as the benchmark value: find an element greater than the benchmark value from left to right as left, and then find an element less than the benchmark value from right to left as right;

Take the leftmost element as the benchmark value: find an element greater than the benchmark value from right to left as left, and then find an element less than the benchmark value from left to right as right;

conclusion

If you look from left to right first, and then from right to left, the elements where left and right coincide must be greater than or equal to the reference value, so you should put the reference value used for exchange at the end of the array

If you first look from right to left, and then from left to right, the elements where left and right coincide must be less than or equal to the reference value, so you should put the reference value used for exchange at the front of the array

Implementation of quick sort

The core process of quick sort code implementation:

1. First, sort out the whole interval into the following: the left side is less than or equal to the benchmark value, and the right side is greater than or equal to the benchmark value;

2. Then recursively sort out the left section and the right section respectively.

Code implementation: there are no detailed comments

package java2021_1015;

import java.util.Arrays;

public class TestSort2 {
    public static void quickSort(int[] array){   
        quickSortHelper(array,0,array.length-1);  
    }
//Recursive process of quick sort
    private static void quickSortHelper(int[] array, int left, int right) {        
        if(left>=right){            
            return ;
        }       
        int index = partition(array,left,right);//After finishing sorting at the same time, return the index subscript
        quickSortHelper(array,left,index-1);
        quickSortHelper(array,index+1,right);
    }
// The partition operation is performed by means of left and right pointers
    private static int partition(int[] array, int left, int right) {
        int begin=left;//Subscript of left element
        int end=right;//Subscript of right element
        int base=array[right];//Reference value
        while(begin<end){           
            while(begin < end && array[begin]<=base){// Array [begin] < = base: indicates that the current element is smaller than the benchmark value
                begin++;//Find next element
            }           
            while(begin < end && array[end]>=base){// Array [End] > = base if the current element is larger than the benchmark value
                end--;//Find next element
            }                      
            swap(array,begin,end);
        }      
        swap(array,begin,right);//right is the subscript of the last position in a sequence       
        return begin;
    }
// Exchange operation
    private static void swap(int[] array, int i, int j) {
        int tmp = array[i];
        array[i] = array[j];
        array[j] = tmp;
    }
    public static void main(String[] args) {
        int[] array={9,5,2,7,3,6,8};
        quickSort(array);
        System.out.println(Arrays.toString(array));
    }
}

Code implementation: This is a detailed comment, big head!!

package java2021_1015;

import java.util.Arrays;
/**
 * Description:Quick sort
 */
public class TestSort2 {
    public static void quickSort(int[] array){
        //Create a method to help complete recursion to help complete the recursion process
        quickSortHelper(array,0,array.length-1);
        //Parameter array: indicates which part of the array is recursive
        //0,array.length-1: given an interval range, the recursion is divided into a front closed and back closed interval by 0,array.length-1
        // The division of front closed and back closed intervals is mainly for the sake of code simplicity
    }
//Recursive process of quick sort
    private static void quickSortHelper(int[] array, int left, int right) {
        //The decision is made in this method
        if(left>=right){
            //At this time, it means that there are 0 or 1 elements in the interval. Because it is closed before and closed after, when left=right is yes, there is also one element. Sorting is not required at this time
            return ;//Just return directly
        }
        //Sort out the [left,right] section
        //Create a clean-up method partition separately
        //The return value of index is the coincidence position of left and right after sorting. Knowing this position, we can distinguish the left and right intervals, and then carry out recursion further
        int index = partition(array,left,right);//After finishing sorting at the same time, return the index subscript
        quickSortHelper(array,left,index-1);
        quickSortHelper(array,index+1,right);
    }
// The partition operation is performed by means of left and right pointers
    private static int partition(int[] array, int left, int right) {
        int begin=left;//Subscript of left element
        int end=right;//Subscript of right element
        //Take the rightmost element as the reference value
        int base=array[right];//Reference value
        while(begin<end){
            //Find elements larger than the reference value from left to right
            //Cycle condition: the subscript of the left element < the subscript of the right element & & the value of the element corresponding to the current left subscript < = reference value
            while(begin < end && array[begin]<=base){// Array [begin] < = base: indicates that the current element is smaller than the benchmark value
                begin++;//Find next element
            }
            //When the above loop ends, either begin and end coincide, or i points to a value greater than base
            //Find the element smaller than the benchmark value from right to left. Initially, end = right.array[end] is equal to base.
            //At this time, skip the reference value directly and always keep the reference value in place.
            while(begin < end && array[end]>=base){// Array [End] > = base if the current element is larger than the benchmark value
                end--;//Find next element
            }
            //When the above loop ends, i and j either coincide or j points to a value less than base

            //The next swap method performs the swap operation
            swap(array,begin,end);
        }

        //[thinking] why can we still meet the order requirements of fast scheduling after the following exchange?
        //When begin and end coincide, the last step is to exchange the elements at the coincident position with the reference value
        //right this is the subscript of the last position in a sequence. It is required that the elements at the coincident position of begin and end must be elements greater than or equal to the reference value before they can be placed at the end
        //How to prove that the element of the found begin position must be > = the reference value?
        /*a)If it is caused by begin + +, it coincides with end
            At this time, the final value depends on the value pointed to by end in the last cycle. In the last cycle, end should find an element less than the benchmark value and exchange it with an element greater than the benchmark value.
            The final end here must be an element greater than the reference value
          b)If it is caused by end -- and coincides with begin
             At this time, the loop exit of begin + + above must be because an element larger than the benchmark value is found at the begin position, and the end and begin coincide, and the final element must be greater than or equal to the benchmark value*/
        swap(array,begin,right);//right is the subscript of the last position in a sequence
        //Why is this exchange reasonable? We should always consider the size relationship between the elements at the coincident position and the reference value. Only those that meet the requirements can be exchanged. The derivation process can be combined with the code
        return begin;

    }
// Exchange operation
    private static void swap(int[] array, int i, int j) {
        int tmp = array[i];
        array[i] = array[j];
        array[j] = tmp;
    }
    public static void main(String[] args) {
        int[] array={9,5,2,7,3,6,8};
        quickSort(array);
        System.out.println(Arrays.toString(array));
    }
}
Print results:
 [2, 3, 5, 6, 7, 8, 9]

Performance analysis of quick sort

The time complexity has been analyzed when solving the relationship between the efficiency of quick sorting and the benchmark value.

Time complexity

best	average	worst
O(N*(logN))	O(N*(logN))	O(N^2)

Spatial complexity: the spatial complexity of fast scheduling mainly lies in recursion. The deeper the recursion, the more space it takes. On average, the depth of recursion is logN. At worst, the depth of recursion is n (when the benchmark value happens to be the maximum or minimum value).

best	average	worst
O(log(N))	O(log(N))	O(N)

Stability of quick sort: unstable sort (equality cannot be determined).

Fast sorting in non recursive way

Non recursive way to achieve rapid sorting, with the help of stack to simulate the recursive process.

Code implementation:

    //Non recursive way to achieve rapid sorting, with the help of stack to simulate the recursive process.
    public  static void quickSortByLoop(int[] array){
        //stack is used to store array subscripts, which indicate the next interval to be processed
        Stack<Integer> stack = new Stack<>();
        //Initially, the right boundary is subscripted into the stack, and then the left boundary is subscripted into the stack. The left and right boundaries still form the front closed and back closed interval
        stack.push(array.length-1);//Right section stacking
        stack.push(0);//Left section stack
        while(!stack.isEmpty()){
            //The order of fetching elements should be exactly opposite to the order of push, because the stack is first in and last out
            int left=stack.pop();
            int right=stack.pop();
            if(left>=right){
                //If the conditions are met, it indicates that there are only 1 or 0 elements in the interval and no sorting is required
                continue;
            }
            //By calling partition, the interval is sorted into a form centered on the benchmark value, with the left less than or equal to the benchmark value and the right greater than or equal to the benchmark value
            int index = partition(array,left,right);
            //Prepare to process the next interval, and stack the interval on the right side of the benchmark value and the interval on the left side of the benchmark value
            //[index+1,right] interval on the right side of benchmark value
            stack.push(right);
            stack.push(index+1);

            //[left,index-1] left range of benchmark value
            stack.push(index-1);
            stack.push(left);
        }
    }
    public static void main(String[] args) {
        int[] array={9,5,2,7,3,6,8};
        quickSortByLoop(array);
        System.out.println(Arrays.toString(array));
    }
}
//Print results
[2, 3, 5, 6, 7, 8, 9]

It would be better to draw a recursive process with your own code.

Optimization of quick sort

1. Optimize the selection of reference value. It is very important to select the reference value, and the method of how much to take the middle is usually used;

• That is, take the middle of the three elements (the leftmost element, the middle position element and the rightmost element, take the middle value as the reference value, and swap the confirmed reference value to the end or start of the array to pave the way for the subsequent sorting action).

2. When the interval is already relatively small, the efficiency of recursion is not high, so instead of continuing recursion, insert sorting can improve the efficiency of fast scheduling;

3. If the interval is very large, the recursion depth will be very deep. When the recursion depth reaches a certain level, recursion may occupy a lot of space. At this time, the sorting of the current interval can be optimized by heap sorting.

8, Merge sort (important)

Principle and process of merging and sorting

• The basic idea of merging and sorting comes from two problems: merging two ordered linked list arrays into one to ensure that the merged linked list or array is still orderly.
• Recursive operation is also necessary for merging and sorting.

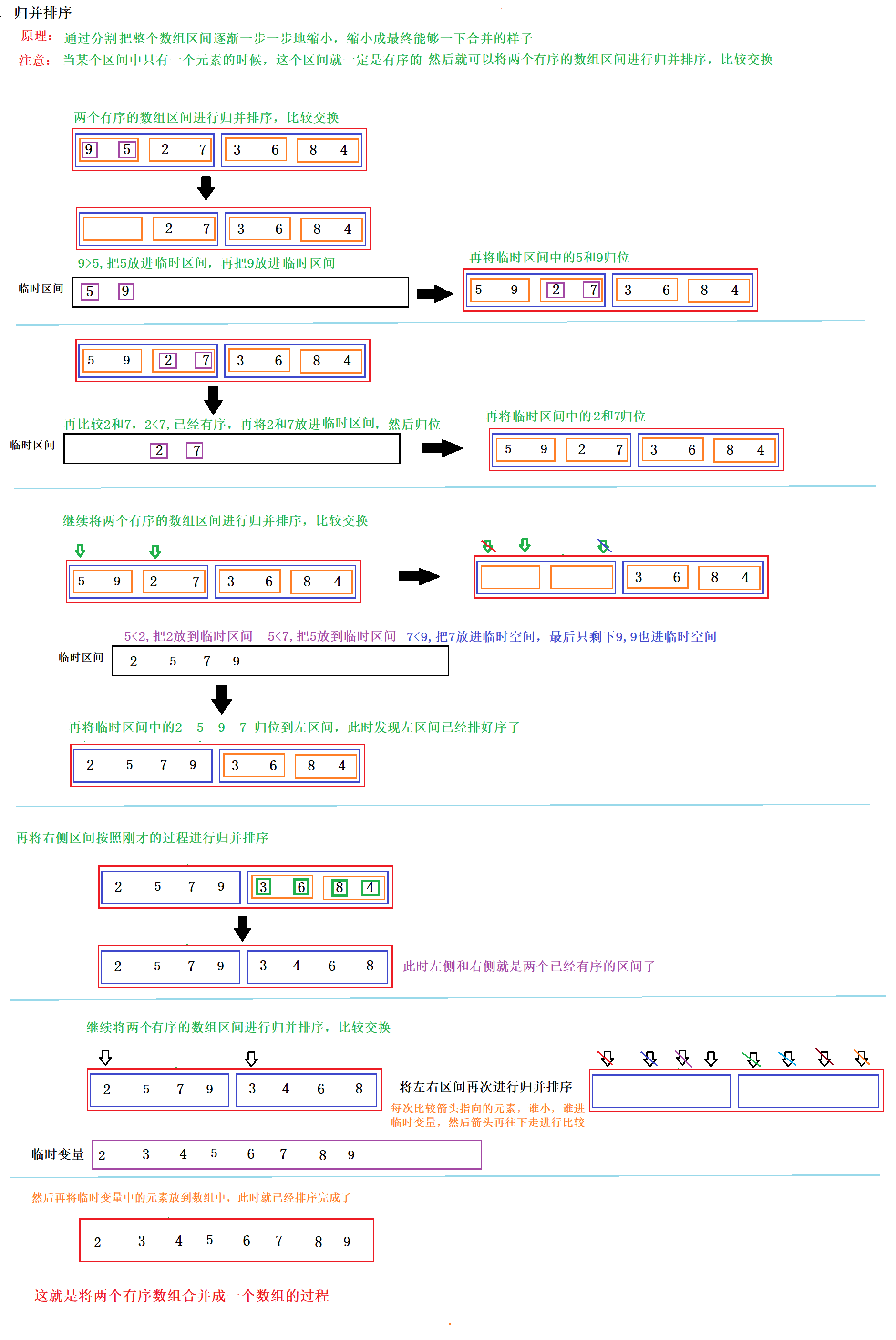
If you don't want to read the picture or don't understand the picture very well, watch a dance of merging and sorting to understand it, which may be more interesting!

Merge sort dance

Implementation of merge sort

Code implementation:

//Merge and sort
//Write a merge method to represent the merging of two arrays
//low, mid, high indicates subscript
//[low,mid): is an ordered interval
//[mid,high): is an ordered interval
//To merge these two ordered intervals into an ordered interval.
    public static void merge(int[] array,int low,int mid,int high) {
        //Set a temporary interval
        int[] output = new int[high-low];
        int outputIndex=0;//Record how many elements are put into the current output array for tailoring
        int cur1 = low;//Starting subscript of the first interval
        int cur2 = mid;//Starting subscript of the second interval
//Enter cycle
        while(cur1 < mid && cur2 < high){//End condition of two intervals
            if(array[cur1] <= array[cur2]){//The judgment condition is written as less than or equal here to ensure stability
                //Compare cur1 and cur2, which is bigger and which is smaller
                //If cur1 is small, put cur1 into the temporary interval
                output[outputIndex] = array[cur1];
                outputIndex++;//The arrow goes back
                cur1++;
            }else {
                output[outputIndex] = array[cur2];
                outputIndex++;
                cur2++;
            }
        }
        //When the above loop ends, one of cur1 or cur2 must reach the end first, and the other has some content left
        //Copy the rest to the output
        while(cur1 < mid){
            output[outputIndex] = array[cur1];
            outputIndex++;
            cur1++;
        }
        //The two loops execute only one
        while(cur2 < high){
            output[outputIndex] = array[cur2];
            outputIndex++;
            cur2++;
        }
        //Move the elements in the output back to the original array
        for(int i = 0; i < high - low;i++){
            array[low+i]  = output[i];
        }
    }
 //Write a merge sort operation to divide the interval
    public static void mergeSort(int[] array){
        //Write an auxiliary method for recursion
        mergeSortHelper(array,0,array.length);
    }
//[low,high) is the front closed and back open interval. If the difference between the two is less than or equal to 1, there are only 0 elements or 1 element in the interval
    private static void mergeSortHelper(int[] array, int low, int high) {
        //Recursive process
        //Handling 1 element
        if(high - low <= 1){
            //[low,high) is the front closed and back open interval. If the difference between the two is less than or equal to 1, there are only 0 elements or 1 element in the interval. At this time, there is no need to merge and return directly
            return;
        }
        //Handling multiple elements
        int mid=(low+high)/2;//Take an intermediate value Mid. with mid, you can divide it into two intervals
        //After this method is executed, it is considered that low and mid have been sorted
        mergeSortHelper(array,low,mid);//Start low, end mid, merge
        //After this method is executed, it is considered that mid and high have been sorted
        mergeSortHelper(array,mid,high);//mid start, high end, merge

        //When the left and right intervals have been merged and sorted, it indicates that the left and right intervals are ordered
        //Next, you can merge the two ordered intervals
        merge(array,low,mid,high);
    }

    public static void main(String[] args) {
        int[] array={9,5,2,7,3,6,8};
        mergeSort(array);
        System.out.println(Arrays.toString(array));
    }
}
//Print results
[2, 3, 5, 6, 7, 8, 9]

Let's take part of the recursion according to the code

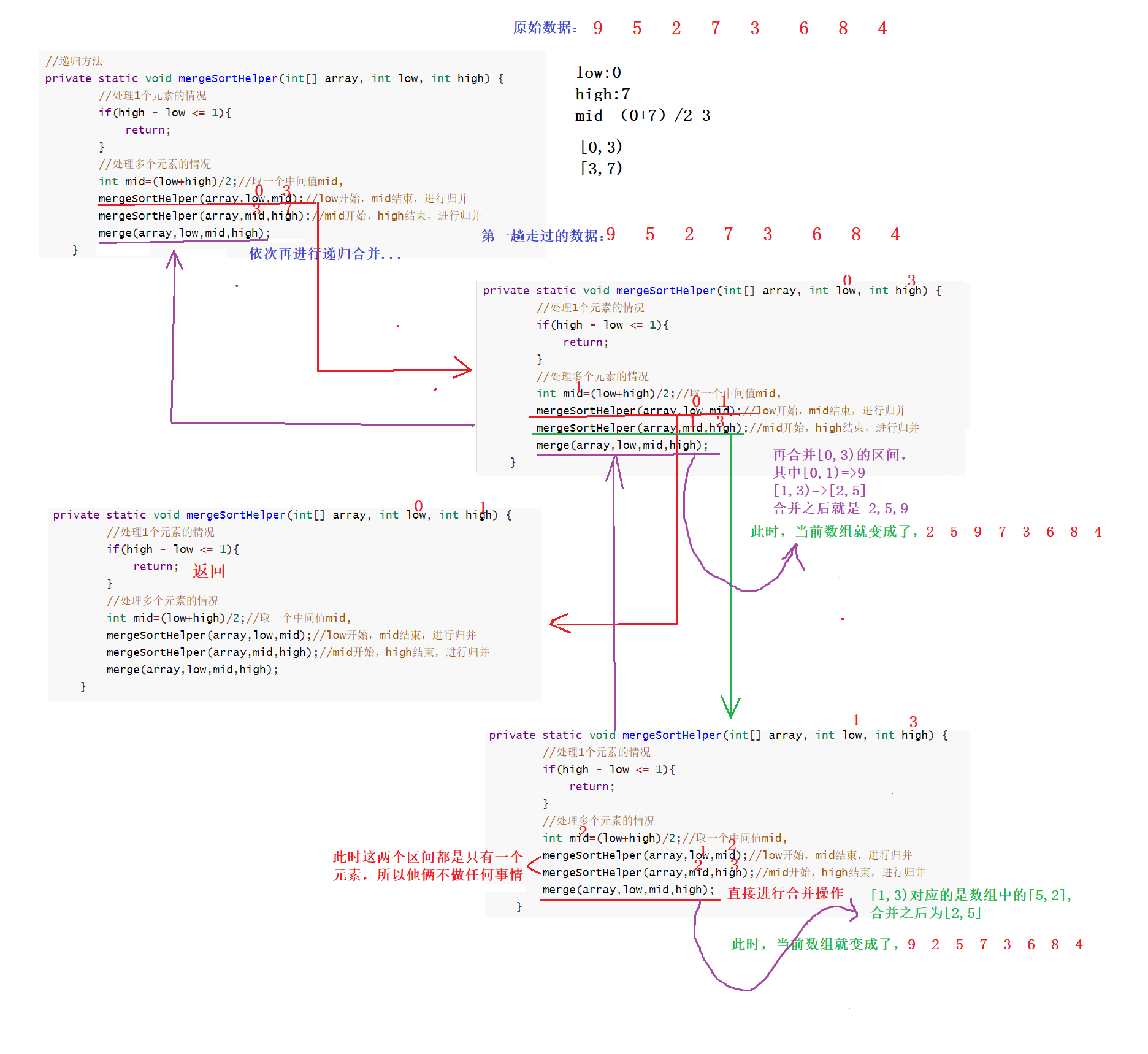
Performance analysis of merge sort

Time complexity of merging and sorting: O(NlogN);

Space complexity of merging and sorting: it has an additional temporary space output, the space is O(N), and it also has a space logN occupied by recursion, so the space complexity is O(N)+O(logN)=O(N), but this is for the space complexity of array merging. If it is a linked list, its space complexity can be O(1)

Stability of merge sort: stable sort is related to the following code

Non recursive implementation of merge sort

Non recursive implementation can be completed through reasonable grouping without stack.

//Non recursive implementation of merge sort
    public static  void mergeSortByLoop(int[] array){
        //A gap variable is introduced for grouping, and the gap variable is used to represent the grouping. Gap is the difference of subscripts between two adjacent groups, and gap also represents the length of each group
        //When gap is 1, [0] [1] merges, [2] [3] merges, [4] [5] merges, [6] [7] merges, and so on... The numbers here represent subscripts
        //When gap is 2, [0,1] and [2,3] are merged, [4,5] and [6,7] are merged, and so on
        //When gap is 4, [0,1,2,3] and [4,5,6,7] are merged, and so on
        for(int gap = 1; gap < array.length;gap *= 2){
            //Next, perform specific grouping and merging
            //The following loop is executed once to complete the merging of two adjacent groups
            for(int i = 0;i < array.length;i += 2*gap){
                //The current adjacent group is [begin, mid] [mid, end)
                int begin = i;
                int mid = i + gap;
                int end = i + 2*gap;
                //If it exceeds the return value, it is assigned to prevent the subscript from crossing the boundary
                if(mid > array.length){//If mid is out of range
                    mid = array.length;
                }
                if(end > array.length){//If mid is out of range
                    end = array.length;
                }
                merge(array,begin,mid,end);//Call merges to merge the ranges of begin, mid and end
            }
        }
    }
    public static void main(String[ ] args) {
        int[] array={9,5,2,7,3,6,8};
        mergeSortByLoop(array);
        System.out.println(Arrays.toString(array));
    }
}
//Print results:
[2, 3, 5, 6, 7, 8, 9]

Characteristics of merging and sorting

Merge sort has two important characteristics. It can be used for external sort and linked list sort

For example, it can solve the sorting problem of massive data

External sorting: the sorting process needs to be performed in external storage such as disk

Premise: the memory is only 1G, and the data to be sorted is 100G

Because all data cannot be put down in memory, external sorting is required, and merge sorting is the most commonly used external sorting

1. First, divide the documents into 200 copies, each 512 M
2. Sort 512 M respectively, because the memory can be placed, any sort method can be used
3. Conduct 200 channels of merging, and do the merging process for 200 ordered documents at the same time, and the final result will be orderly.

9, Sort summary

The performance of each sorting should also be mastered and memorized!!!

Sorting method	Time complexity – best	average	worst	Spatial complexity	stability
Bubble sorting	O(n)	O(n^2)	O(n^2)	O(1)	stable
Insert sort	O(n)	O(n^2)	O(n^2)	O(1)	stable
Select sort	O(n^2)	O(n^2)	O(n^2)	O(1)	instable
Shell Sort	O(n)	O(n^1.3)	O(n^2)	O(1)	instable
Heap sort	O(n * log(n))	O(n * log(n))	O(n * log(n))	O(1)	instable
Quick sort	O(n * log(n))	O(n * log(n))	O(n^2)	O(log(n))-O(n)	instable
Merge sort	O(n * log(n))	O(n * log(n))	O(n * log(n))	O(n)	stable

Focus on the code implementation and performance analysis of each sort. The principle and process should also be combined with the code to deeply understand the basic idea of each sort.