paper

[1] Bi Xiaowei, Li Bin, Wang Yuqiang, Chen Shihua, Peng Ping, Lei Tao. Multi star up processing and down transmission data conflict optimization decision method based on directed graph model [J]. Electronic information countermeasure technology, 2020,35 (06): 46-49 + 77

HowNet connection

https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CJFD&dbname=CJFDLAST2020&filename=DZDK202006010&uniplatform=NZKPT&v=WUV2Ik7FqzXaHjBD%25mmd2FnWqjhA5Yz2PUEnIlWmPNj0bkXtaf%25mmd2BUH2CE8TIx0lroT0e0F

Directed graph model

That is, the classical model in graph theory. For graph G(V,E), it is basically composed of vertices and edges between vertices. Edges have weight and direction, and each vertex may contain other attribute information.

The most classical solution problem in graph theory is the path finding problem, that is, given the start node and end node, looking for the optimal path for the objective function, taking the shortest path as the objective function, that is, it degenerates to looking for the shortest path from the start vertex to the end vertex

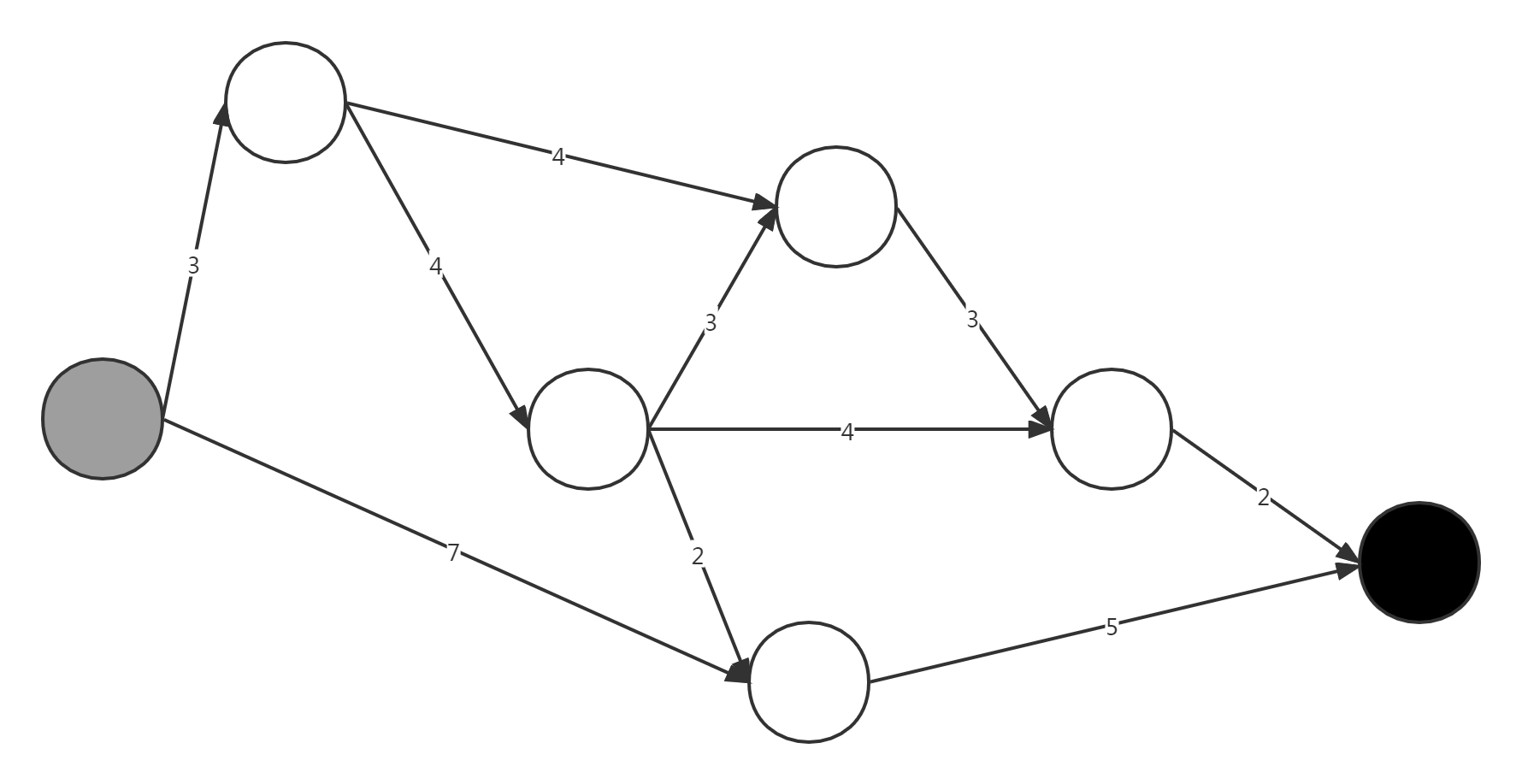
Satellite multi satellite data transmission

When the ground receiving terminal receives the satellite data transmission, it can only be in the time window visible to the satellite. When the ground receiving terminal simultaneously receives the satellite data transmission downlink request exceeding the upper limit of its own receiving equipment within a given time period, a multi satellite downlink data conflict occurs.

Solving model

This paper gives a simple and easy to understand solution model, that is, in a given planning time period, the visible time windows of satellites and ground receiving equipment are sorted according to the arrival order.

Each vertex of the graph corresponds to an executable satellite downlink data task.

If there is no overlap in the time period between the two downlink tasks, it is considered that the two tasks do not conflict, that is, task A can be completely executed. At the same time, Task B can be executed after the equipment adjusts the stable time. Then there is A directed edge from task A to Task B, and the weight of the edge corresponds to the overhead information of task switching.

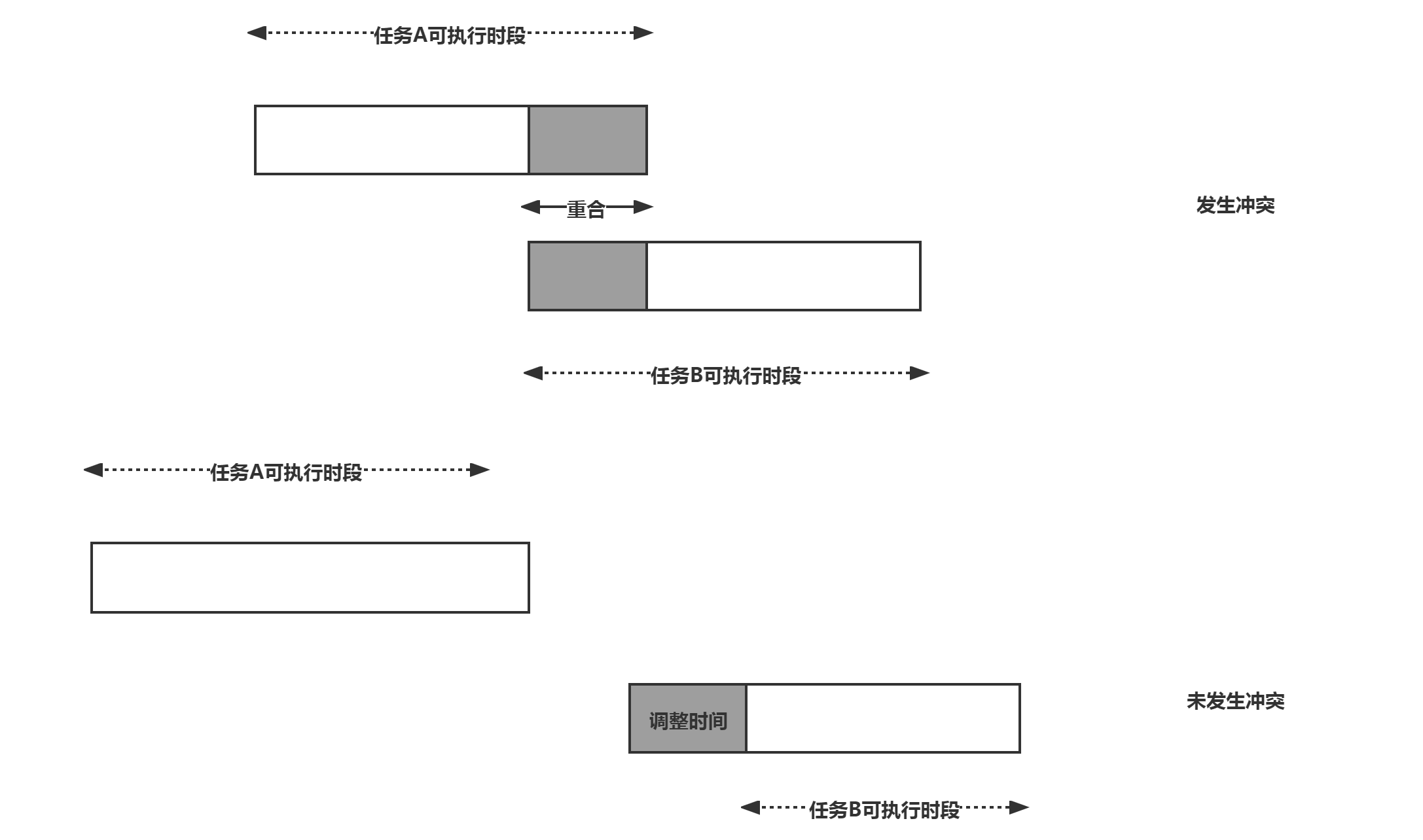
For the two tasks without conflict, it is considered that there is a directed edge, then the final problem is to find an optimal path from the beginning to the end.

At the same time, different objective functions may lead to different final task execution sequences

Optimization objective of multi satellite downlink mission

Optimization criteria	explain
Maximize mission planning benefits	The importance of the data transmitted by each satellite is different, that is, the weight value corresponding to each vertex is different. To maximize the revenue of task planning, it is required to maximize the sum of the revenue of vertices on the planned path
Maximize the number of mission plans	Considering the balance of each satellite's data transmission occupying ground resources, the data of each satellite should be transmitted in the planning window as much as possible, so the number of nodes passing through the planning path should be as many as possible

The final weight of each edge is comprehensively calculated according to the above two criteria. The weight of each impact factor is given by the domain prior knowledge. If 1 has a greater weight, focus on the final planning income; if 2 has a greater weight, focus on the final number of planning tasks.

Find the path with the greatest benefit

This paper adopts the shortest path Dijkstra algorithm to solve the maximum return path, but does not give a detailed solution idea

This paper provides a solution idea. The shortest path algorithm is to find the shortest path combined with the weight of the edge, but the weight of this problem is the income value of each vertex, so the problem is transformed into finding the maximum weight path. The idea is as follows:

First, add two auxiliary vertices V_start,V_end, and then solve the single source maximum return path.

The pseudo code is as follows:

int num_of_point = 100;
int m_min = -1;
int test_length = 1000;

int max_path(vector<vector<int>> m_map)   //map[i][j] stores the revenue from I to j. during initialization, if and only if I - > j are directly connected, it is initialized with the observed revenue of j task, otherwise it is initialized to 0
{

	vector<int> dis(num_of_point, m_min);//The cumulative value of equity from initialization vertex to all other vertices is - 1
	vector<bool> visit(num_of_point, false);//Initialize all nodes, that is, they are not added to the calculated set
	visit[0] = true;//The starting point of the search is V[0]


	//Initialize the dis array. If there are edges, DIS is the weight value of the corresponding vertex. Otherwise, it is - 1
	for (int i = 1; i < num_of_point; i++)
	{
		if (m_map[0][i] >0)  //There are directed edges
		{
			dis[i] = m_map[0][i];
		}
		else
			dis[i] = m_min;//If there is no directed edge, the return to the corresponding vertex is - 1



	}



	//Add the vertices with the greatest benefit in the subsequent order, and update the original path (if possible)

	for (int i = 0; i < num_of_point; i++)
	{

		int index = -1;
		int m_max = -1;
		for (int j = 1; j < num_of_point; j++)
		{
			if (visit[j] == false && dis[j] > m_max)
			{
				m_max = dis[j];
				index = j;
			}


		}

		visit[index] = true;//Flag bit accessed

		for (int j = 1; j < num_of_point; j++)  //Update possible greater interests
		{

			if (m_map[index][j] > 0 && dis[j] < dis[index] + m_map[index][j])  //When the introduction of index makes it from the starting point to index + index - > J (that is, index and j need to be directly connected)
			{
				dis[j] = dis[index] + m_map[index][j];
			}
		}

		//After completion, traverse the maximum value in dis

	}

	int res = -1;
	for (int i = 1; i < num_of_point; i++)
	{
		res = max(res, dis[i]);
	}

	return res;

}