Path planning -- Application of dynamic programming in Apollo Planner and C + + code implementation

Posted by petersro on Thu, 04 Nov 2021 09:50:50 +0100

What is dynamic programming (DP)

Bellman optimal principle

the characteristic of multi-stage decision-making process is that decisions must be made in each stage. The strategy of decision-making process with N stages is a decision sequence composed of n successive stage decisions. Since the termination state of the previous stage is the initial state of the later stage, the optimal decision-making in the determination stage can not only start from the effect of this stage, but must be considered comprehensively and planned as a whole. In other words, the optimal decision of stage k should not only be the optimization of this stage, but must be the overall optimization of this stage and all subsequent stages, that is, the optimal decision about the whole rear sub process. On the basis of in-depth research, Behrman puts forward the famous optimality principle of multi-stage decision-making according to the characteristics of multi-stage decision-making process with no aftereffect:
The optimal strategy of the whole process has such a property: no matter what the past state and decision of the process are, for the state formed by the previous decision, the remaining decisions must constitute the optimal strategy. In short, the meaning of the optimality principle is that any molecular strategy of the optimal strategy must also be optimal.

dynamic programming algorithm

Path selection algorithm based on dynamic programming

In EM planner, path selection is based on S-L coordinate system, which is mainly divided into the following steps:

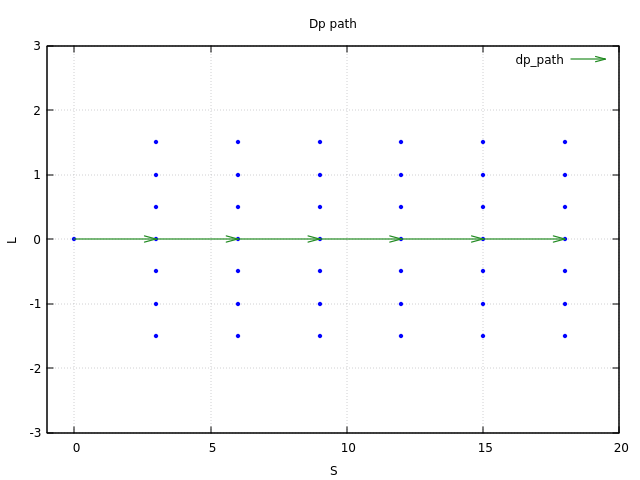
Road sprinkling point
The scattering rules are mainly determined by the following aspects: vehicle width, vehicle position, lane width, vehicle speed, maximum step size of scattering point (S and L directions), minimum step size of scattering point (S and L directions), minimum length of scattering point, maximum length of scattering point, etc;
Using DP to generate the path with the lowest Cost

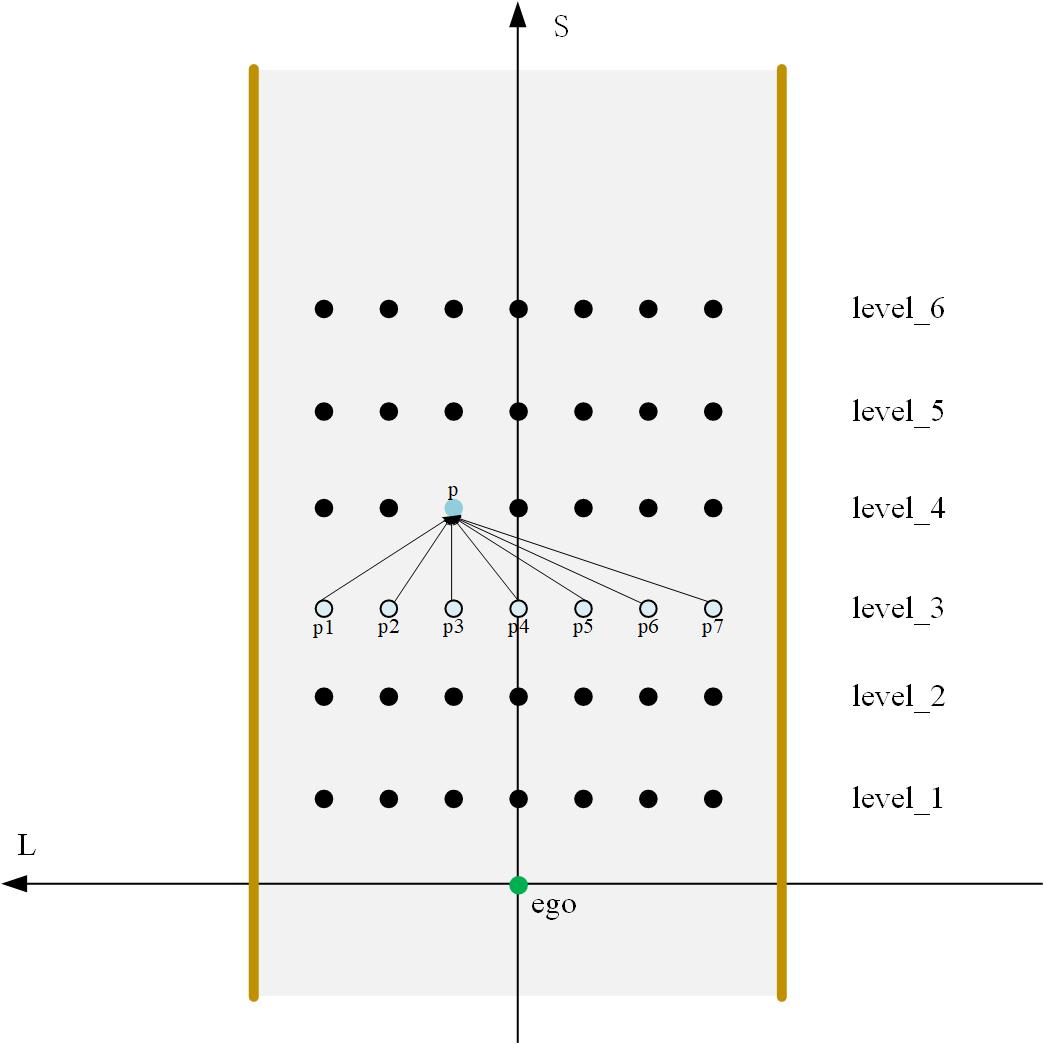
As shown in the figure above, the cost of point p is calculated as follows:
p . c o s t = s t d : : m i n { p 1 . c o s t + R 1 , . . . , p 7 . c o s t + R 7 } p.{cost} = std::min\{p_1.cost + R_1, ..., p_7.cost +R_7\} p.cost=std::min{p1.cost+R1,...,p7.cost+R7}.
Among them, R 1 R_ one R1 = slave node p 1 p_ one p1 to node p p The price of P.

C + + code implementation

// node.h file
struct SlPoint {
  SlPoint(const double _s, const double _l) : s(_s), l(_l) {
  }
  double s;
  double l;
};

struct Node {
  Node(const SlPoint& _sl_point)
      : sl_point(_sl_point), pre_node(nullptr), cost(std::numeric_limits<double>::max()) {
  }
  SlPoint sl_point;
  Node* pre_node;
  double cost;
};

// class DpPath file
class DpPath final {
 public:
  explicit DpPath(const std::vector<std::vector<SlPoint>>& sample_points,
                  const std::vector<Box2d>& obstacles);

  bool Search(std::vector<SlPoint>* const path);

 private:
  void Init(const std::vector<std::vector<SlPoint>>& sample_points);

  void CalculateCostTable();

  void CalculateCostAt(const int32_t l, const int32_t s);

  double CalculateAllObstacleCost(const SlPoint& pre_point, const SlPoint& cur_point) const;

  double CalculateObstacleCost(const Box2d& obs, const Box2d& veh) const;

  double CalculateReferenceLineCost(const SlPoint& pre_point, const SlPoint& cur_point) const;

 private:
  std::vector<std::vector<Node>> cost_table_;
  std::vector<Box2d> obstacles_;
  const double vehicle_length_ = 2.0;
  const double vehicle_width_ = 1.0;
};

DpPath::DpPath(const std::vector<std::vector<SlPoint>>& sample_points,
               const std::vector<Box2d>& obstacles)
    : obstacles_(obstacles) {
  CHECK_GT(sample_points.size(), 1);
  CHECK_EQ(sample_points.front().size(), 1);
  Init(sample_points);
}

bool DpPath::Search(std::vector<SlPoint>* const path) {
  CHECK(path!=nullptr);

  CalculateCostTable();
  auto& last_level = cost_table_.back();
  Node* min_cost_node = nullptr;
  double min_cost = std::numeric_limits<double>::max();
  for (auto& p : last_level) {
    if (p.cost < min_cost) {
      min_cost = p.cost;
      min_cost_node = &p;
    }
  }
  if (min_cost_node == nullptr || min_cost == std::numeric_limits<double>::max()) {
    return false;
  }

  while (min_cost_node != nullptr) {
    path->emplace_back(min_cost_node->sl_point);
    min_cost_node = min_cost_node->pre_node;
  }
  std::reverse(path->begin(), path->end());
  return true;
}

void DpPath::Init(const std::vector<std::vector<SlPoint>>& sample_points) {
  for (const auto& level : sample_points) {
    std::vector<Node> level_points;
    for (const auto& p : level) {
      level_points.emplace_back(p);
    }
    cost_table_.emplace_back(level_points);
  }
}

void DpPath::CalculateCostTable() {
  cost_table_[0][0].cost = 0.0;
  for (uint32_t s = 1; s < cost_table_.size(); ++s) {
    for (uint32_t l = 0; l < cost_table_[s].size(); ++l) {
      CalculateCostAt(s, l);
    }
  }
}

void DpPath::CalculateCostAt(const int32_t s, const int32_t l) {
  auto& pre_level = cost_table_[s - 1];
  double min_cost = std::numeric_limits<double>::max();
  for (auto& pre_point : pre_level) {
    double cost = CalculateAllObstacleCost(pre_point.sl_point, cost_table_[s][l].sl_point) +
                  CalculateReferenceLineCost(pre_point.sl_point, cost_table_[s][l].sl_point);
    cost += pre_point.cost;
    if (cost < min_cost) {
      min_cost = cost;
      cost_table_[s][l].pre_node = &pre_point;
      cost_table_[s][l].cost = min_cost;
    }
  }
}

double DpPath::CalculateAllObstacleCost(const SlPoint& pre_point, const SlPoint& cur_point) const {
  const double curve_length = cur_point.s - pre_point.s;
  QuinticPolynomialCurve1d curve(pre_point.l, 0.0, 0.0, cur_point.l, 0.0, 0.0, curve_length);
  double cost = 0.0;
  constexpr double kStep = 0.1;
  for (double s = 0.0; s < curve_length; s += kStep) {
    double vehicle_l = curve.Evaluate(0, s);
    double vehicle_s = pre_point.s + s;
    double vehicle_heading = std::atan(curve.Evaluate(1, s));
    Box2d veh({vehicle_s, vehicle_l}, vehicle_heading, vehicle_length_, vehicle_width_);
    for (const auto& obs : obstacles_) {
      cost += CalculateObstacleCost(obs, veh);
    }
  }
  return cost;
}

double DpPath::CalculateObstacleCost(const Box2d& obs, const Box2d& veh) const {
  if (obs.HasOverlap(veh)) {
    return std::numeric_limits<double>::max();
  }
  const double dis = obs.DistanceTo(veh);
  if (dis > 2 * vehicle_width_) {
    return 0.0;
  }
  return 1.0 / (dis + std::numeric_limits<double>::epsilon());
}

double DpPath::CalculateReferenceLineCost(const SlPoint& pre_point,
                                          const SlPoint& cur_point) const {
  const double curve_length = cur_point.s - pre_point.s;
  QuinticPolynomialCurve1d curve(pre_point.l, 0.0, 0.0, cur_point.l, 0.0, 0.0, curve_length);
  double cost = 0.0;
  constexpr double kStep = 0.1;
  for (double s = 0.0; s < curve_length; s += kStep) {
    double l = curve.Evaluate(0, s);
    cost += std::fabs(l * l);
  }
  return cost;
}

// test file
class DpPathTest : public ::testing::Test {
 public:
  void SetUp() {
    SlPoint vehicle_position(0.0, 0.0);
    sample_points_.emplace_back(std::vector<SlPoint>{vehicle_position});
    for (double s = 3; s < 20; s += 3) {
      std::vector<SlPoint> level_points;
      for (double l = -1.5; l < 2.0; l += 0.5) {
        level_points.emplace_back(s, l);
      }
      sample_points_.emplace_back(level_points);
    }
  }

 protected:
  std::shared_ptr<DpPath> dp_path_ = nullptr;
  std::vector<std::vector<SlPoint>> sample_points_;
  std::vector<Box2d> obstacles_;
};

TEST_F(DpPathTest, Search1) {
  dp_path_ = std::make_shared<DpPath>(sample_points_, obstacles_);
  std::vector<SlPoint> path;
  bool ret = dp_path_->Search(&path);
  EXPECT_TRUE(ret);
  EXPECT_GT(path.size(), 2);
}

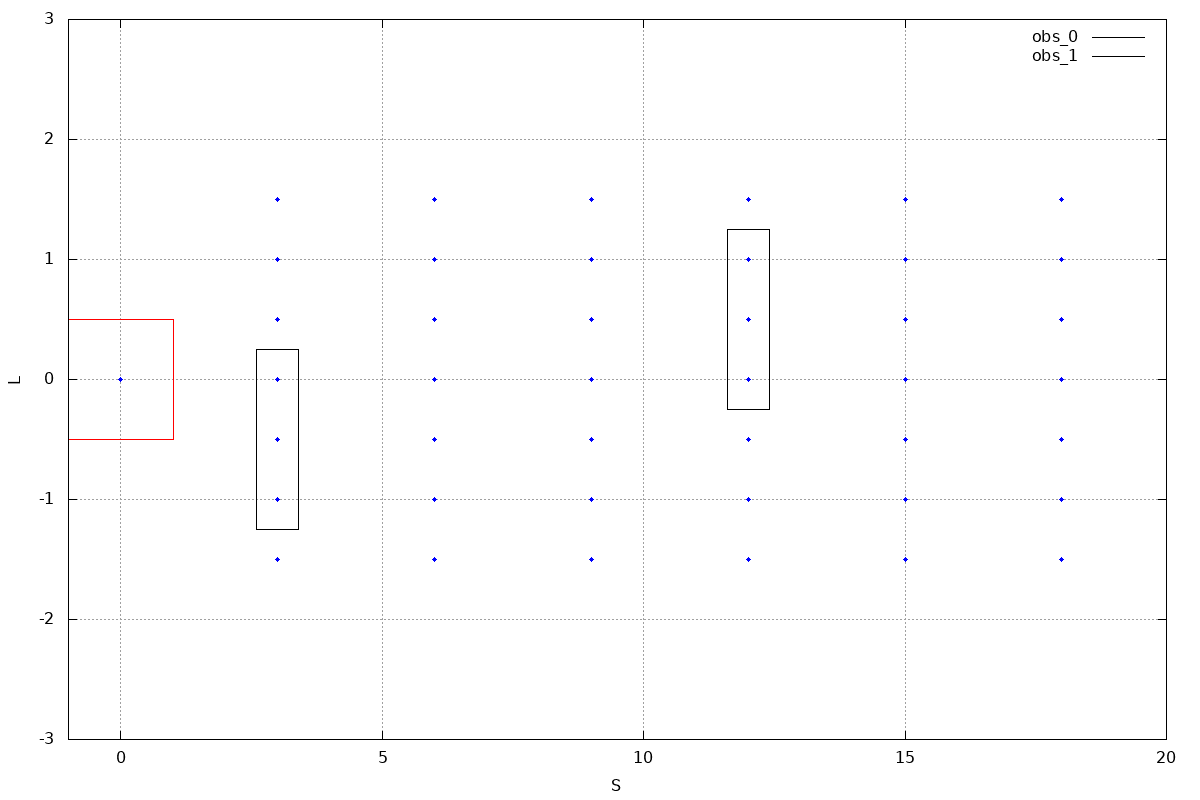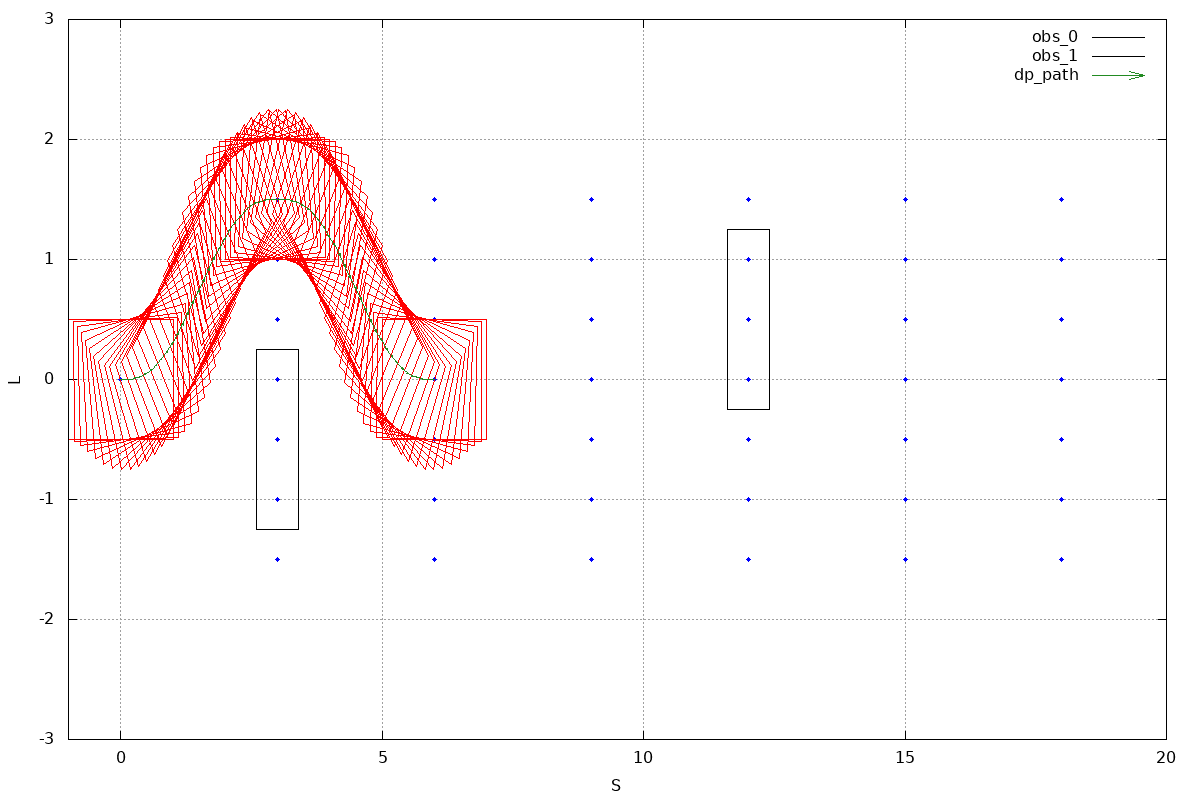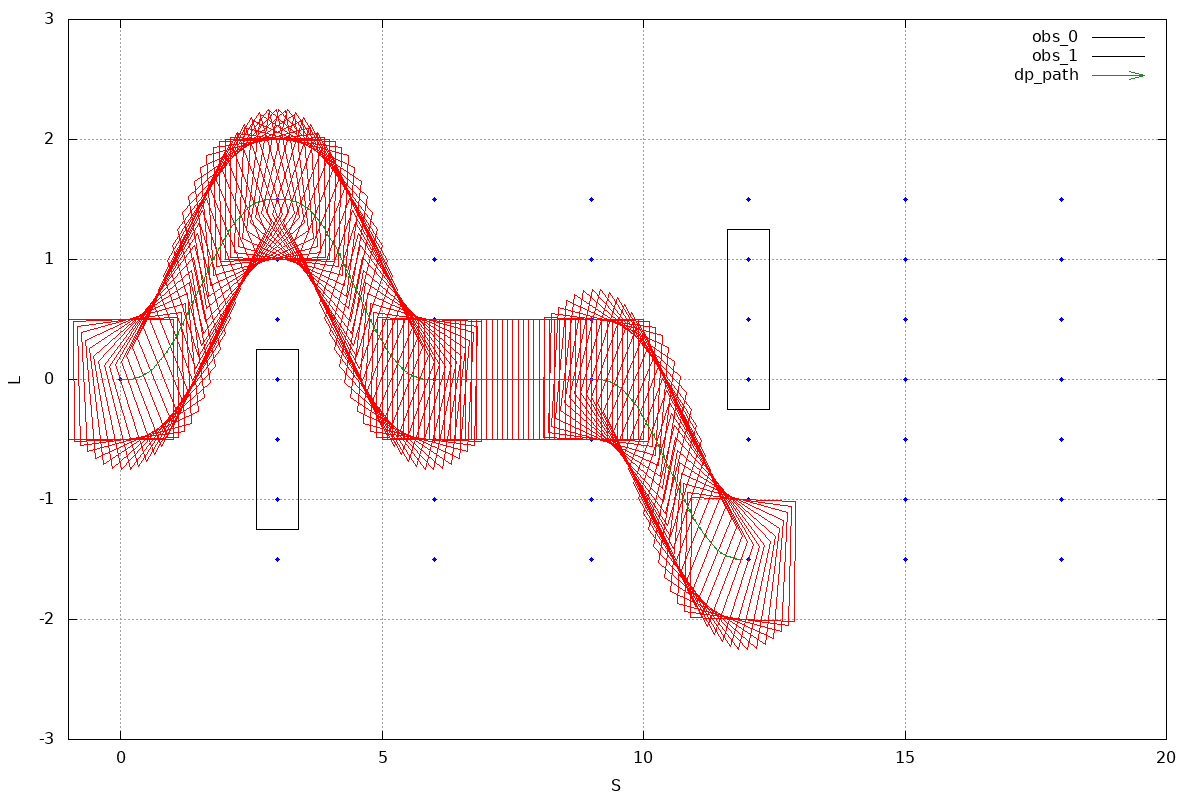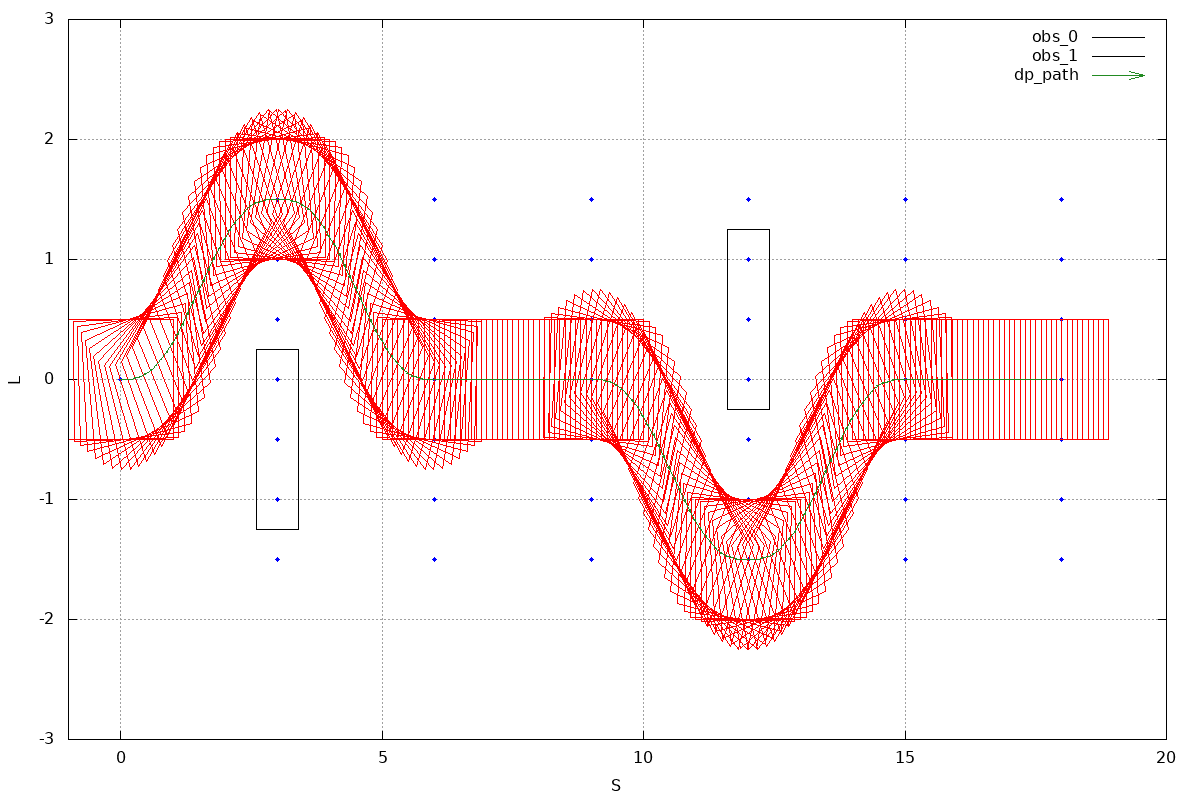
TEST_F(DpPathTest, Search2) {
  Box2d obs1({3, -0.5}, 0.0, 0.8, 1.5);
  Box2d obs2({12, 0.5}, 0.0, 0.8, 1.5);
  obstacles_.emplace_back(obs1);
  obstacles_.emplace_back(obs2);
  dp_path_ = std::make_shared<DpPath>(sample_points_, obstacles_);
  std::vector<SlPoint> path;
  bool ret = dp_path_->Search(&path);
  EXPECT_TRUE(ret);
  EXPECT_GT(path.size(), 2);
}

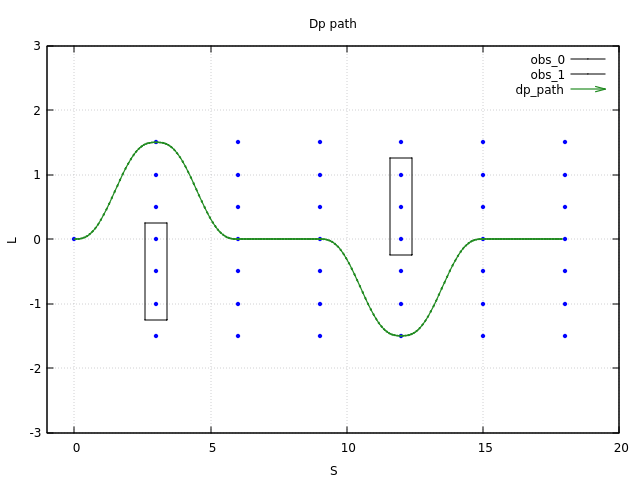
test result

(73 messages) path planning -- Application of dynamic programming in apollo Planner and C + + code implementation_ Fat house happy who - CSDN blog_ apollo dynamic programming

Topics: C++ R Language Dynamic Programming

Programmer Think

Path planning -- Application of dynamic programming in Apollo Planner and C + + code implementation

What is dynamic programming (DP)

Path selection algorithm based on dynamic programming

C + + code implementation

test result

Hot Topics