Task 1-1
To program task1_1.asm assembles and connects, loads and tracks debugging with debug, and answers questions based on the results.
task1_1.asm
assume ds:data, cs:code, ss:stack data segment db 16 dup(0) ; 16 byte units are reserved, and the initial values are 0 data ends stack segment db 16 dup(0) ;16 byte units are reserved, and the initial values are 0 stack ends code segment start: mov ax, data mov ds, ax mov ax, stack mov ss, ax mov sp, 16 ; Set stack top mov ah, 4ch int 21h code ends end start
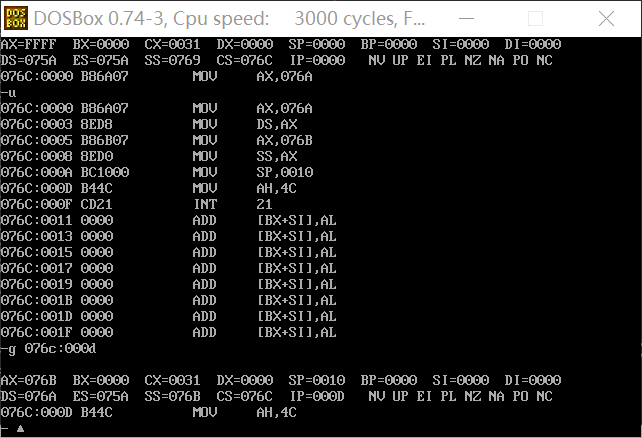
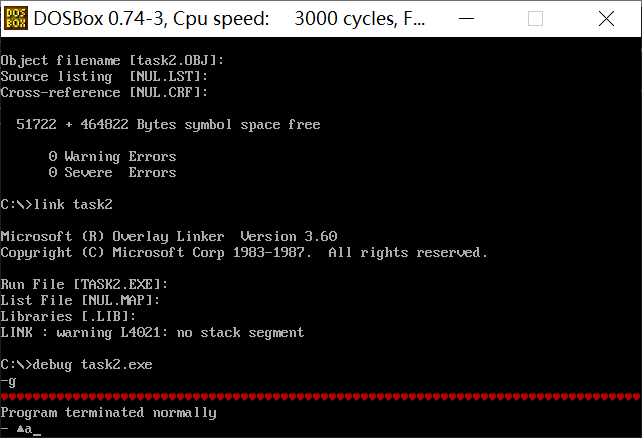
① In debug, it will be executed until the end of line17 and before line19. At this time, record: register (DS) = 076AH__, Register (SS)=
_ 076BH___， Register (CS) =_ 076CH___
② Assuming that the segment address of the code segment is X after the program is loaded, the segment address of the data segment is X_ x-2___， The segment address of stack is_ x-1__.
Task 1-2
To program task1_2.asm assembles and connects, loads and tracks debugging with debug, and answers questions based on the results.
task1_2.asm
assume ds:data, cs:code, ss:stack
data segment
db 4 dup(0) ; Four byte units are reserved, and the initial value is 0
data ends
stack segment
db 8 dup(0) ; 8 byte units are reserved, and the initial values are 0
stack ends
code segment
start:
mov ax, data
mov ds, ax
mov ax, stack
mov ss, ax
mov sp, 8 ; Set stack top
mov ah, 4ch
int 21h
code ends
end start
① In debug, execute until the end of line17 and before line19. Record this time: register (DS) =_ 076AH___， Register (SS)=
076BH____， Register (CS) =_ 076CH___
② Assuming that the segment address of the code segment is X after the program is loaded, the segment address of the data segment is X_ x-2___， The segment address of stack is_ x-1___.
Task 1-3
To program task1_3.asm assembles and connects, loads and tracks debugging with debug, and answers questions based on the results.
task1_3.asm
assume ds:data, cs:code, ss:stack
data segment
db 20 dup(0)
data ends
stack segment
db 20 dup(0)
stack ends
code segment
start:
mov ax, data
mov ds, ax
mov ax, stack
mov ss, ax
mov sp, 20
mov ah, 4ch
int 21h
code ends
end start
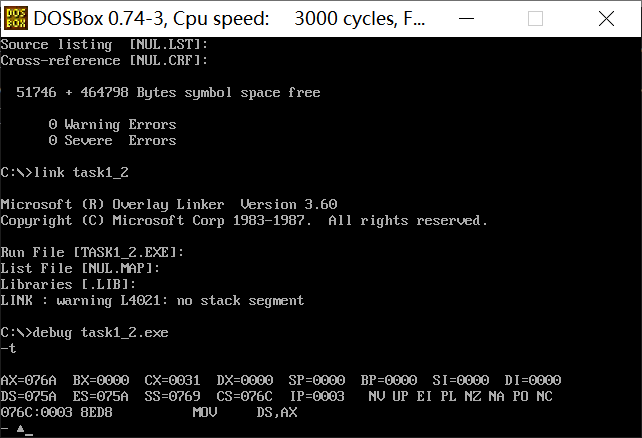
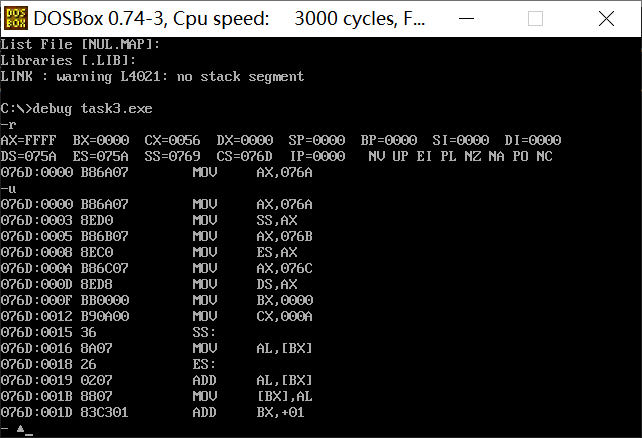
① In debug, execute until the end of line17 and before line19. Record this time: register (DS) =_ 076AH___， Register (SS)=
__ 076CH__， Register (CS) =_ 076EH___
② Assuming that the segment address of the code segment is X after the program is loaded, the segment address of the data segment is X_ x-64___， The segment address of stack is_ x-32___.
Tasks 1-4
To program task1_4.asm assembles and connects, loads and tracks debugging with debug, and answers questions based on the results.
task1_4.asm
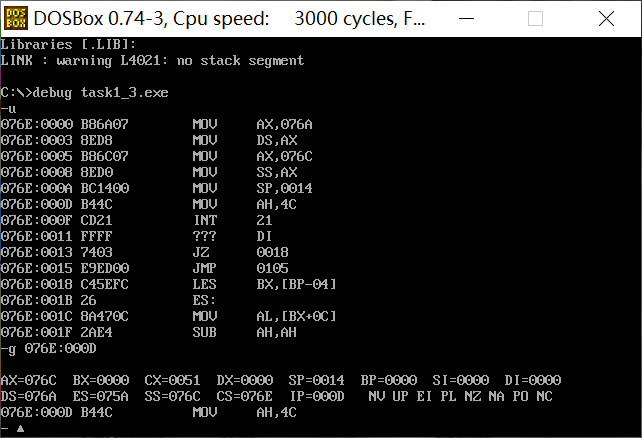
assume ds:data, cs:code, ss:stack
code segment
start:
mov ax, data
mov ds, ax
mov ax, stack
mov ss, ax
mov sp, 20
mov ah, 4ch
int 21h
code ends
data segment
db 20 dup(0)
data ends
stack segment
db 20 dup(0)
stack ends
end start
① In debug, execute until the end of line9 and before line11. Record this time: register (DS) =_ 076CH___， Register (SS)=
_ 076EH___， Register (CS) =___ 076AH_
② Suppose that after the program is loaded, the segment address of the code segment is x__, Then, the segment address of the data segment is_ x+32___， The segment address of stack is
__x+64__.
Tasks 1-5
Based on the practice and observation of the above four experimental tasks, summarize and answer:
① For the segment defined below, after the program is loaded, the actual memory space allocated to the segment is_ (N/16+1)*16___.
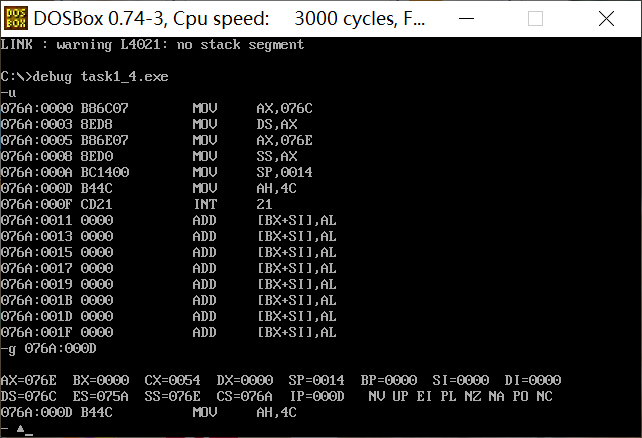
② If the pseudo instruction end start is changed to end in the programs task1_1.asm, task1_2.asm, task1_3.asm and task1_4.asm, which program can still be executed correctly? Analyze and explain the reasons in combination with the conclusions obtained from practical observation.
Task1_4 can be executed correctly. Because end start indicates the program execution entry, the code segment of task1_4 is at the beginning of the program. If end start is changed to end, it can still be executed normally
2. Experimental task 2
Write an assembly source program to realize 160 consecutive bytes to memory units b800:0f00 ~ b800:0f9f, and fill hexadecimal numbers repeatedly in turn
According to 03 04.
assume cs:code
code segment
start:
mov ax, 0b800h
mov ds, ax
mov bx, 0f00h
mov cx, 80
s:mov [bx], 0403h
add bx, 2
loop s
mov ah, 4ch
int 21h
code ends
end start
Tips:
1. In task 3 of Experiment 1, we did experiments to achieve the same effect, but we filled it through the f command of debug at that time
Second, programming is required.
In debug, use the f command to batch fill in data to memory cells.
-f b800:0f00 0f9f 03 04
Fill the memory unit interval b800:0f00 ~ b800:0f9f for 160 consecutive bytes, and fill hexadecimal data 03 and 04 repeatedly in turn.
2. When programming, pay attention to the problems of hexadecimal and byte order. After writing, run the program. If the result is different from that of experiment task 3 of Experiment 1
To, indicating that there is an error in programming.
3. Experimental task 3
It is known that the 8086 assembly source program task3.asm code fragment is as follows.
task3.asm
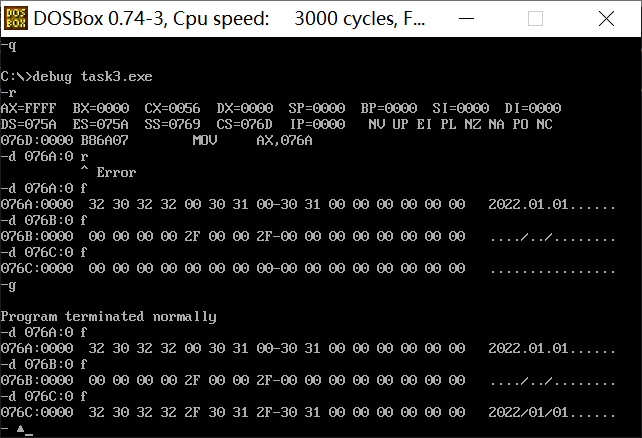
assume cs:code
data1 segment
db 50, 48, 50, 50, 0, 48, 49, 0, 48, 49 ; ten numbers
data1 ends
data2 segment
db 0, 0, 0, 0, 47, 0, 0, 47, 0, 0 ; ten numbers
data2 ends
data3 segment
db 16 dup(0)
data3 ends
code segment
start:
mov ax, data1
mov ss, ax
mov ax, data2
mov es, ax
mov ax, data3
mov ds, ax
mov bx, 0
mov cx, 10
s:mov al, ss:[bx]
add al, es:[bx]
mov [bx], al
add bx, 1
loop s
mov ah, 4ch
int 21h
code ends
end start
requirement:
① The programming adds the data of logical segment data1 and logical segment data2 in turn, and the results are saved in logical segment data3.
② Load, disassemble and debug in debug. Before and after the data items are added in turn, view the three logical segments data1 respectively,
Confirm that the memory space corresponding to data2 and data3 is added one by one to ensure that the result exists in the logical segment data3.
4. Experimental task 4
It is known that the 8086 assembly source program task4.asm code fragment is as follows.
task4.asm
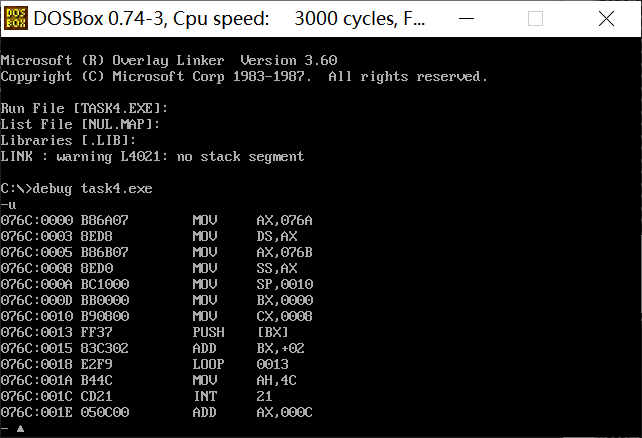
assume cs:code, ss:data1, ds:data2
data1 segment
dw 2, 0, 4, 9, 2, 0, 1, 9
data1 ends
data2 segment
dw 8 dup(?)
data2 ends
code segment
start:
mov ax, data1
mov ds, ax
mov ax, data2
mov ss, ax
mov sp, 10h
mov bx, 0
mov cx, 8
s:push [bx]
add bx, 2
loop s
mov ah, 4ch
int 21h
code ends
end start
requirement:
① Complete the program to store the eight word data in logical segment data1 in reverse order in logical segment b.
② After assembly and connection, load the program in debug and run it to line15. Before the program exits, use the d command to view the data corresponding to data segment data2
Memory space, confirm whether the subject requirements are met.
It did
5. Experimental task 5
Use any text editor to enter the assembly source program task5.asm.
task5.asm
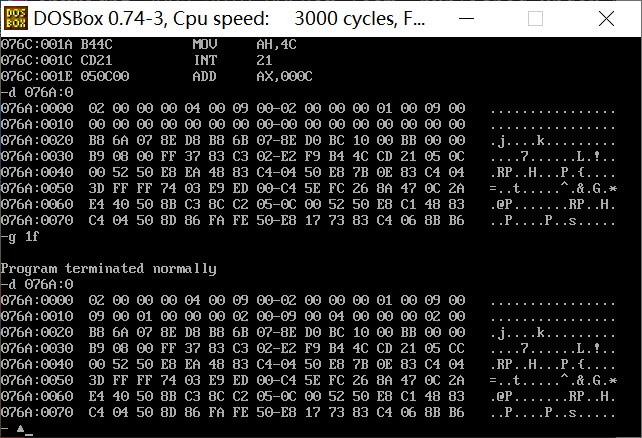
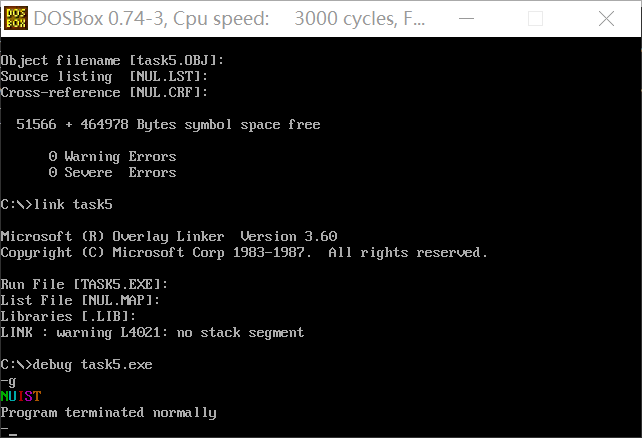
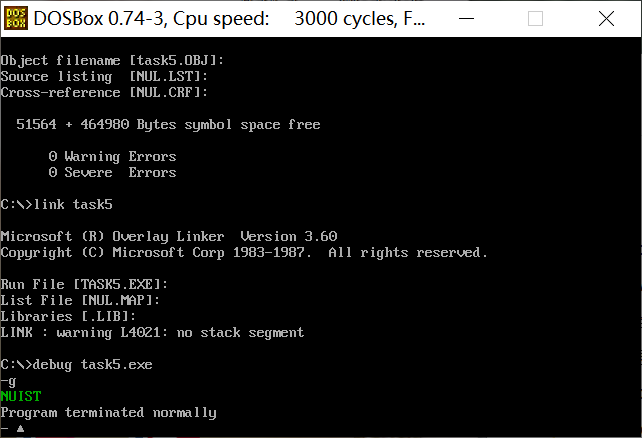
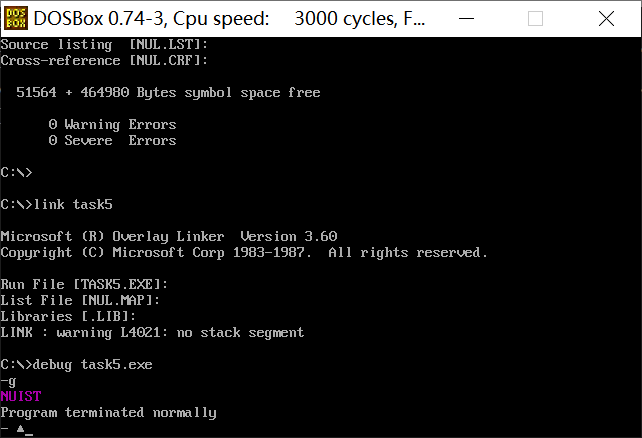
assume cs:code, ds:data
data segment
db 'Nuist'
db 2, 3, 4, 5, 6
data ends
code segment
start:
mov ax, data
mov ds, ax
mov ax, 0b800H
mov es, ax
mov cx, 5
mov si, 0
mov di, 0f00h
s: mov al, [si]
and al, 0dfh
mov es:[di], al
mov al, [5+si]
mov es:[di+1], al
inc si
add di, 2
loop s
mov ah, 4ch
int 21h
code ends
end start
Read the source program, theoretically analyze the functions of the source code, especially line15-25, what are the functions realized by the loop, and understand the functions of each instruction line by line.
Assemble and link the program to get the executable file, run and observe the results.
Use the debug tool to debug the program. Before the program returns, that is, after line25 and before line27, observe
result.
The function of line19 in the source code is that line19 in the source code combines the data and binary number 11011111 in the storage unit bit by bit, that is, convert lowercase letters into uppercase letters.
Modify the values of the five byte units in line4, reassemble, link, run, and observe the results. The purpose of the byte data of line4 in the data section of the source code is to set the character color.
Based on observation, analyze and guess what the numerical function here is.
6. Experimental task 6
It is known that the 8086 assembly source program task6.asm code fragment is as follows.
task6.asm
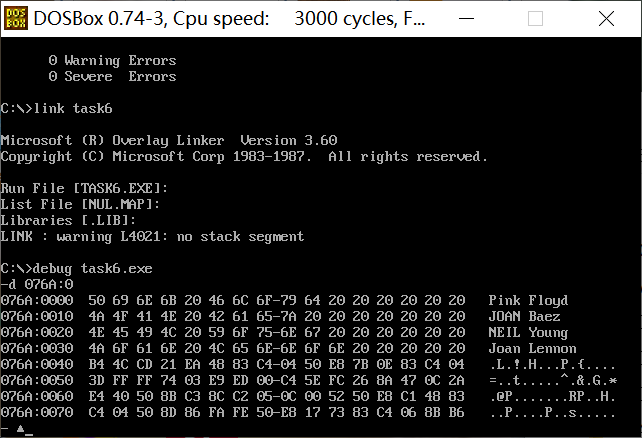
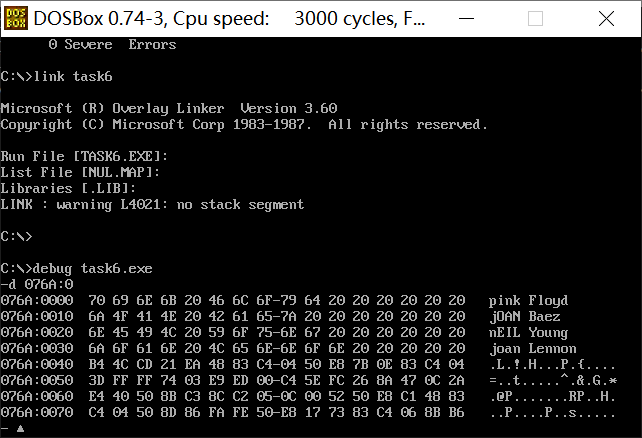
assume cs:code, ds:data
data segment
db 'Pink Floyd '
db 'JOAN Baez '
db 'NEIL Young '
db 'Joan Lennon '
data ends
code segment
start:
mov ax, data
mov ds, ax
mov bx, 0
mov cx, 4
s:mov ax, cx
mov cx, 4
t:or byte ptr [bx], 20h
inc bx
loop t
add bx, 12
mov cx, ax
loop s
mov ah, 4ch
int 21h
code ends
end start
requirement:
① Complete the program and change the first word of each line in the data section from uppercase to lowercase.
② Load the program in debug, disassemble it, and check the memory space corresponding to the data section with the d command before exiting line13. Confirm that the first word in each line has changed from uppercase to lowercase.
Confirm implementation
7. Experimental task 7
Problem scenario description:
The basic information of Power idea from 1975 to 1979 is as follows:
These data have been defined in the logical segment data (line4-6) of program task7.asm.
task7.asm
assume cs:code, ds:data, es:table
data segment
db '1975', '1976', '1977', '1978', '1979'
dw 16, 22, 382, 1356, 2390
dw 3, 7, 9, 13, 28
data ends
table segment
db 5 dup( 16 dup(' ') ) ;
table ends
code segment
start:
mov ax, data
mov ds, ax
mov ax, table
mov es, ax
mov si, 0
mov di, 0
mov dx, 0
mov bx, 0
mov cx, 5
s:mov ax, word ptr ds:[di]
mov word ptr es:[bx], ax
mov ax, word ptr ds:[di].2
mov word ptr es:[bx].2, ax
mov ax, word ptr ds:[si].20
mov word ptr es:[bx].7, ax
mov ax, word ptr ds:[si].30
mov word ptr es:[bx].10, ax
mov ax, ds:[si].20
mov dl, ds:[si].30
div dl
mov byte ptr es:[bx].14, al
add di, 4
add si, 2
add bx, 16
loop s
mov ah, 4ch
int 21h
code ends
end start
requirement:
① Complete the program, realize the title requirements, and write the year, income, number of employees and per capita income into the table section in a structured way.
In the table, each row of data occupies 16 bytes in the logical segment table, and the byte size of each data is allocated as follows. During the period, the data are separated by spaces.
② After assembly and connection, load and debug the program in debug. Use u command, g command and d command flexibly and reasonably to display the data information of the logical segment table at the beginning, and the data information of the data segment table after structurally storing the data to confirm the realization of the problem requirements
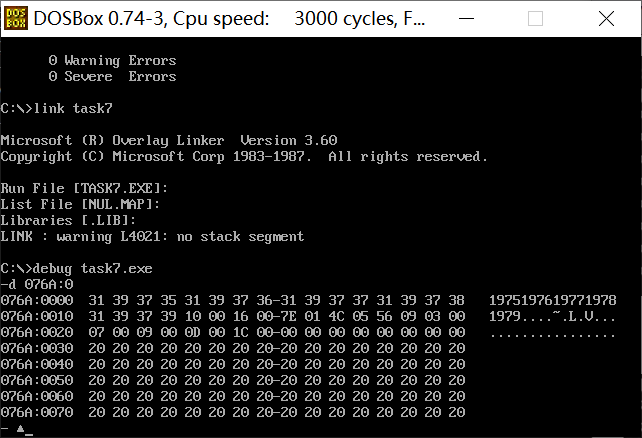
Problem: unable to write data