catalogue
4. Simulation implementation of stack
5. Differences between stack, virtual machine stack and stack frame
1. Concept of stack
Stack is a special linear table. It can only be inserted and deleted at the fixed end. The end for data insertion and deletion is the top of the stack and the other end is the bottom of the stack. The elements in the stack follow the principle of last in first out (LIFO).
Stack pressing: the operation of inserting data into the stack is called stack entering, stack pressing and stack entering. The input data is at the top of the stack
Stack out: stack deletion is called stack out. The output data is at the top of the stack
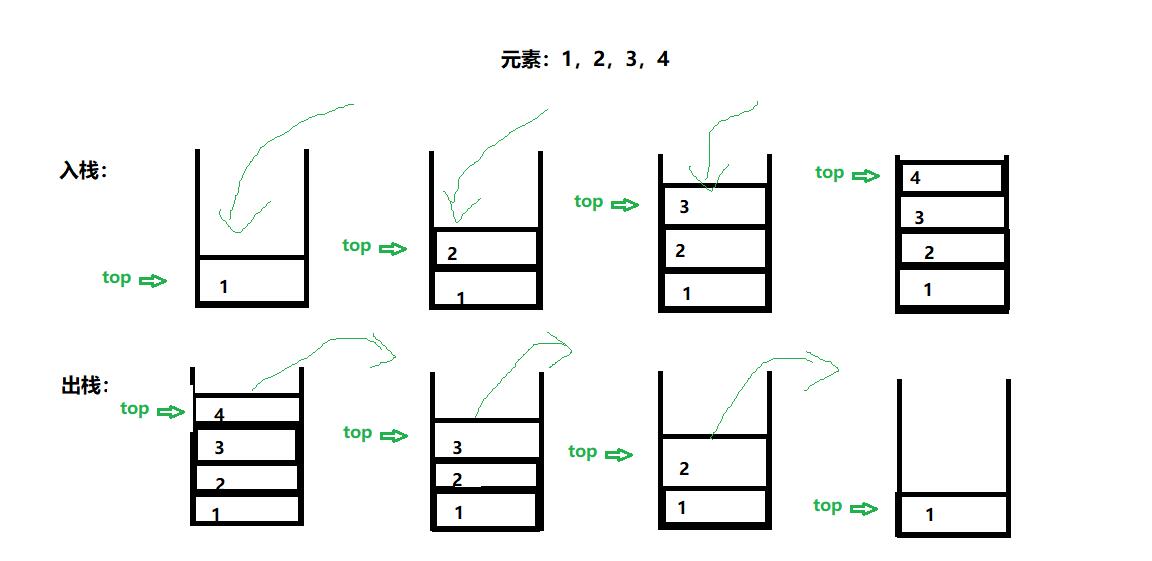
2. Use of stack
| method | Function description |
| Stack() | Construct an empty stack |
| E push(E e) | Stack e and return e |
| E pop() | Take the top element out of the stack and return |
| E peek() | Get stack top element |
| int size() | Gets the number of valid elements in the stack |
| boolean empty() | Check whether the stack is empty |
Show the above methods in Code:
public class TestStack {
public static void main(String[] args) {
Stack<Integer> s = new Stack<>();
s.push(1);
s.push(2);
s.push(3);
s.push(4);
System.out.println(s.size());
s.pop();
System.out.println(s.peek());
if(s.empty()){
System.out.println("Stack empty");
}else{
System.out.println("The stack is not empty. The number of elements is:"+s.size());
}
}
//result:
4
3
Stack is not empty, number of elements: 3Use the stack to convert recursion into a loop:
// Recursive mode
void printList(Node node){
if(null != node){
printList(node.next);
System.out.print(node.val + " ");
}
}
// Cycle mode
void printList(Node node){
if(null == node){
return;
}
Stack<Node> s = new Stack<>();
// Save the nodes in the linked list in the stack
Node cur = node;
while(null != cur){
s.push(cur);
cur = cur.next;
}
// Remove elements from the stack
while(!s.empty()){
System.out.print(s.pop().val + " ");
}
}3. OJ question of stack
1. Bracket matching (LeetCode20) Valid parentheses
You can go to the link above to view the title
method:
1. Get the elements of the string in turn. If the element is an open bracket, put it on the stack
2. If it is not an open bracket, first judge whether the stack is empty. If it is empty, return false. If it is not empty, carry out subsequent operations
3. Compare the element at the top of the stack with the element of the string obtained earlier. If the brackets match, the element at the top of the stack will exit the stack, end the current cycle and continue the subsequent comparison. If the brackets do not match, false will be returned
4. After comparing the elements of the string, judge whether there is any remaining in the stack. If there is any remaining, it returns false, and if there is no remaining, it returns true
Reference code:
class Solution {
public boolean isValid(String s) {
Stack<Character> stack = new Stack<>();
for(int i=0;i<s.length();i++){
char c = s.charAt(i);
if(c=='('||c=='{'||c=='['){
stack.push(c);
}else{
if(stack.empty()){
return false;
}
char top = stack.pop();
if(top=='{'&&c=='}'||top=='['&&c==']'||top=='('&&c==')'){
continue;
}else{
return false;
}
}
}
if(!stack.empty()){
return false;
}
return true;
}
}2. Evaluation of inverse Polish expression (LeetCode150) Inverse Polish expression evaluation
You can go to the link above to view the title
method:
1. Put the string on the stack in turn. If the string is not an arithmetic symbol, put it on the stack
2. When the string is an arithmetic symbol, take the two elements at the top of the stack for arithmetic operation
3. Continue to stack the results of the operation
4. Carry out the above cycle in sequence
5. Finally, return the value of the top element of the stack, that is, the value of the inverse expression
Reference code:
class Solution {
public int evalRPN(String[] tokens) {
Stack<Integer> s = new Stack<>();
for(String e : tokens){
if(!(e.equals("+")||e.equals("-")||e.equals("*")||e.equals("/"))){
s.push(Integer.parseInt(e));//Convert character e to integer
}else{
int right = s.pop();
int left = s.pop();
switch(e) {
case "+":
s.push(left+right);
break;
case "-":
s.push(left-right);
break;
case "*":
s.push(left*right);
break;
case "/":
s.push(left/right);
break;
}
}
}
return s.peek();
}
}3. Stack out and stack in order matching (JZ31) Stack push in and pop-up sequence
method:
1. When the elements in the stack sequence are smaller than the first element in the stack sequence, the elements in the stack sequence are stacked in turn
2. Add 1 to the subscript of the stack sequence for each element
3. When the elements of the stack in sequence are equal to those of the stack out sequence, stack out, and add 1 to the index of the stack out sequence
4. After traversing the elements of the out of stack sequence, return true
Reference code:
class Solution {
public boolean validateStackSequences(int[] pushed, int[] popped) {
Stack<Integer> s = new Stack<>();
int inIndex = 0;
int outIndex = 0;
while(outIndex<popped.length){
while(s.empty()||s.peek()!=popped[outIndex]){
if(inIndex<pushed.length){
s.push(pushed[inIndex]);
inIndex++;
}
else{
return false;
}
}
s.pop();
outIndex++;
}
return true;
}
}4. Simulation implementation of stack
public class MyStack<E> {
E[] array;
int size;
public MyStack(){
array = (E[])new Object[3];
}
public E push(E e){
ensureCapacity();
array[size++] = e;
return e;
}
public E pop(){
E e = peek();
size--;
return e;
}
public E peek(){
if(empty()){
throw new RuntimeException("Stack is empty, unable to get stack top element");
}
return array[size-1];
}
public int size(){
return size;
}
public boolean empty(){
return 0 == size;
}
private void ensureCapacity(){
if(size == array.length){
array = Arrays.copyOf(array, size*2);
}
}
}5. Differences between stack, virtual machine stack and stack frame
Stack: a last in first out data structure inherited from Vector
Virtual machine stack: a memory space with special functions. Stack area: it is thread private and stores information related to function calls, mainly stack frames. It is implemented according to the characteristics of the stack in the data structure
Stack frame: a structure related to function calls. Internal: local variable table, operand stack. When each method runs, JVM creates a stack frame and then presses the stack frame to the virtual machine stack. When the call ends, the corresponding stack frame will stack from the virtual machine stack.