542.01 matrix
in etc. \color{#FFB800} {medium} secondary
Given a matrix mat composed of 0 and 1, please output a matrix of the same size, where each lattice is the distance from the corresponding position element in mat to the nearest 0.
The distance between two adjacent elements is 1.
Example 1:
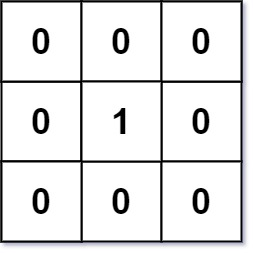
Input: mat = [[0,0,0],[0,1,0],[0,0,0]] Output:[[0,0,0],[0,1,0],[0,0,0]]
Example 2:
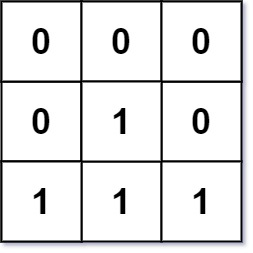
Input: mat = [[0,0,0],[0,1,0],[1,1,1]] Output:[[0,0,0],[0,1,0],[1,2,1]]
Tips:
- m == mat.length
- n == mat[i].length
- 1 <= m, n <= 104
- 1 <= m * n <= 104
- mat[i][j] is either 0 or 1.
- At least one 0 in mat
Method 1: Multi-source breadth first search
Let's focus on the general breadth first search. Let's assume that there is only one 0 in the map.
It is mentioned in the title that each grid is the distance from the corresponding position element in mat to the nearest 0. In turn, the value of each grid is the distance from 0 to this element. In this way, our starting point is much clearer. We can start from the land with the value of 0 for breadth first search. Each time we expand outward, the value of 4 lands around the land is 1; Then expand from the land with a value of 1 to the surrounding 4 grids, the value of the surrounding land is 2, and so on. The value of all land traversed in round i is also i (here i starts counting from 1).
Take a 4x4 mat as an example, where (1,1) is 0. The process is as follows:
_ _ _ _ _ 1 _ _ 2 1 2 _ 2 1 2 3 2 1 2 3 _ 0 _ _ ==> 1 0 1 _ ==> 1 0 1 2 ==> 1 0 1 2 ==> 1 0 1 2 _ _ _ _ _ 1 _ _ 2 1 2 _ 2 1 2 3 2 1 2 3 _ _ _ _ _ _ _ _ _ 2 _ _ 3 2 3 _ 3 2 3 4 Author: LeetCode-Solution Link: https://leetcode-cn.com/problems/01-matrix/solution/01ju-zhen-by-leetcode-solution/ Source: force buckle( LeetCode) The copyright belongs to the author. For commercial reprint, please contact the author for authorization. For non-commercial reprint, please indicate the source.
The above example is from the official problem solution of LeetCode
In addition, we also need an array see to store which lands have been accessed to avoid being added to the queue again. For example, the following example:
1 _ _ 0 1 _ 1 _ _
We have expanded from 0 on the left to 1 in the middle. Next, we should expand in the "top, right and bottom" directions, and the left should be ignored.
We're actually Day 7 In this article 733. Image rendering and 695. Maximum area of the island In these two questions, we have encountered the array used to record whether the land has been accessed. In these two questions, because the land we have traversed is no longer needed, the value of the land is set to 0, and the "value is set to 0" The operation of is equivalent to the operation that we record the land as visited. The array used to record whether it has been visited is abstracted to the map itself. Our final results are useful, so we can't abandon it.
Of course, you can make a judgment. If the value to be given is less than the current value of the land, you can overwrite the original value and join the queue for re expansion, but that's ridiculous. Suppose your matrix is full of 0, and according to this idea, the whole matrix should be traversed once for each 0. After the assignment of the whole matrix is completed, because the value of each land cannot be determined If it is near or near to another 0, the next 0 will traverse the whole (almost) matrix again. Take the following example:
0 0 0 0 0 1 2 3 0 0 1 2 0 0 0 0 0 0 0 0 0 0 0 0 => 1 2 3 4 => 1 1 2 3 => ... => 0 1 1 1 => 0 0 1 1 0 0 0 0 2 3 4 5 2 2 3 4 1 2 2 2 1 1 2 2 0 0 0 0 3 4 5 6 3 3 4 5 2 3 3 3 2 2 3 3
In the final result, since the whole array is 0, the shortest distance from itself to the land with value 0 is 0. Therefore, the result is still 0:
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
First, the outer layer needs a double loop to find each 0 of the original matrix, so the time complexity of the outer layer is O(n2); the inner layer needs a loop. Although it does not need to traverse the whole answer matrix again, it is not like binary search. Removing half of the array each time is O(logn), and here is still the complexity of O(n). Therefore, the time complexity of this idea is O(n3).
However, it is not enough to have only the idea mentioned before. Our idea can only be valid for a matrix with only one 0. We assume that there are two zeros in the matrix, so after the first round of traversal is completed, it should be like this:
_ 1 _ _ 1 0 1 _ _ 1 0 1 _ _ 1 _
According to the above idea, no matter which 0 we start from, we directly traverse the whole matrix, and can not achieve the correct result. Therefore, we need to improve it.
The problem now is that it's hard to determine which 0 to start with. We can start with another problem: what did we do in the second round? We expanded from many 1's to many 2's. then why didn't we encounter the problem of not determining which 1 to start with?
We can find that in the original idea, there is already such a "problem": it starts from many 1s and expands outward together, and it does not become a "problem" , which shows that this process is correct. In that case, the process of starting from many zeros to expand outward must also be correct. In each round of breadth first, the values of all lands expanded outward correspond to the number of rounds. In that case, we directly add all zeros to the queue at the beginning, and we will be able to expand the correct ones after the first round of traversal 1, just as the correct 2 can be extended from many 1.
From this, we can conclude that we maintain the original idea, add all zeros to the queue, and then start together, which is multi-source breadth first search.
This problem is very similar to the sequence traversal of the tree. In the sequence traversal, the nodes in one row are expanded at the same time, and all the nodes in the next row are stored in the queue. However, this problem is to expand all the land with a value of 0 at the same time, and store all the land around them in the queue.
This idea makes us realize that all zeros are also extended from a certain point, which is the same as the concept of [super source point] in the shortest path.
#include <vector>
#include <queue>
using namespace std;
typedef pair<size_t, size_t> dpoint;
class Solution
{
private:
static constexpr dpoint D[4] = {{-1, 0}, {0, -1}, {1, 0}, {0, 1}};
public:
vector<vector<int>> updateMatrix(vector<vector<int>> &mat)
{
const size_t m = mat.size(), n = mat[0].size();
vector<vector<int>> dist(m, vector<int>(n, 0));
vector<vector<bool>> seen(m, vector<bool>(n, false));
queue<dpoint> que;
// Separate the "extension 0" in the first round
for (size_t y = 0; y < m; ++y)
{
for (size_t x = 0; x < n; ++x)
{
if (mat[y][x] == 0)
{
que.emplace(y, x);
seen[y][x] = true;
}
}
}
while (!que.empty())
{
auto [y, x] = que.front();
que.pop();
for (const auto &direction : D)
{
size_t ny = y + direction.first, nx = x + direction.second;
if (0 <= ny && ny < m && 0 <= nx && nx < n && !seen[ny][nx])
{
dist[ny][nx] = dist[y][x] + 1;
que.emplace(ny, nx);
seen[ny][nx] = true;
}
}
}
return dist;
}
};
Complexity analysis
-
Time complexity: O(mn). Each land is added to the queue at most once in breadth first search.
-
Spatial complexity: O(mn). In the worst case, all zeros in the matrix are added to the queue; the spatial complexity of the flag array see is also O(mn); the answer array is not included in the spatial complexity; therefore, the spatial complexity is O(2mn)=O(mn).
Reference results
Accepted 50/50 cases passed (64 ms) Your runtime beats 78.26 % of cpp submissions Your memory usage beats 8.4 % of cpp submissions (33.8 MB)
994. Rotten oranges
in etc. \color{#FFB800} {medium} secondary
In a given grid, each cell can have one of the following three values:
- A value of 0 represents an empty cell;
- A value of 1 represents fresh oranges;
- A value of 2 represents rotten oranges.
Every minute, any fresh orange adjacent to the rotten orange (in 4 positive directions) will rot.
Returns the minimum number of minutes that must elapse until there are no fresh oranges in the cell. If this is not possible, returns - 1.
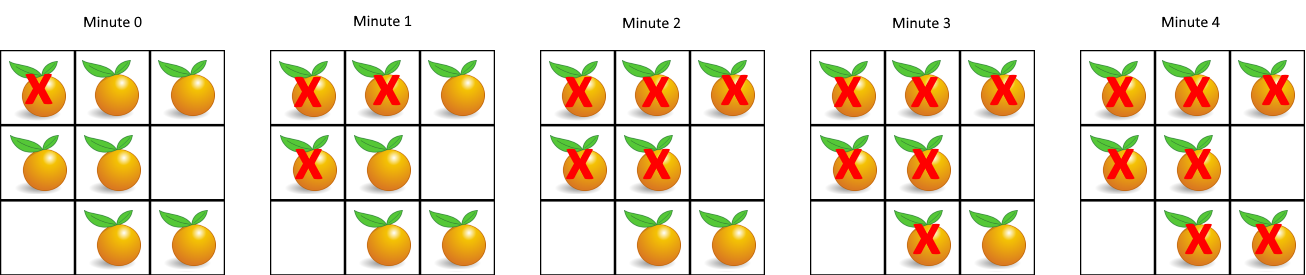
Example 1:
Input:[[2,1,1],[1,1,0],[0,1,1]] Output: 4
Example 2:
Input:[[2,1,1],[0,1,1],[1,0,1]] Output:-1 Explanation: the orange in the lower left corner (row 2, column 0) will never rot, because rot will only occur in four positive directions.
Example 3:
Input:[[0,2]] Output: 0 Explanation: there are no fresh oranges in 0 minutes, so the answer is 0.
Tips:
- 1 <= grid.length <= 10
- 1 <= grid[0].length <= 10
- grid[i][j] is only 0, 1, or 2
Method 1: Multi-source breadth first search
If you use breadth in this question, you should understand that there is a relationship between the topic and breadth.
The title says:
Every minute, any fresh orange adjacent to the rotten orange (in 4 positive directions) will rot.
This sentence can be understood as: expand from rotten oranges around once, change the land value of 1 to 2, and add it to the queue.
In this way, we can find all the land with the value of 2 from the matrix and add them to the queue according to the idea of the previous question. It is equivalent to expanding multiple 0s to multiple 1s in the previous question.
We start from source point 2 and record the distance from the land with value 1 to source point 2. In this way, the decay time of each orange is the distance. Since our original array stores the state of oranges, we need another array to store each distance.
We have three methods, and the reason for these three methods is: in the current idea, the value in the original array in the breadth first process can not be directly used as the basis for whether it has been traversed. Later, we will mention the optimization of this method, using only the original array.
- Above 542.01 matrix In question 1, we set the see array to store whether the land has been traversed. The original array is covered as the distance from each land to the nearest 0.
- We can exchange the two, choose to cover the array to store whether the land has been traversed, and another new array dist stores the distance between each fresh orange (1) and 2
- We can also integrate two arrays into one array. Keep the original array, and all lands in the new array dist are initially set to - 1. In addition, the corresponding position of rotten orange 2 in the map is set to 0. In this way, we can judge whether - 1 has been traversed, and the value of other grids is the distance from fresh oranges to rotten oranges.
Since the first idea has appeared above, the second one is basically similar to the first one. Therefore, we adopt the third train of thought.
Another small problem in this question is that some fresh oranges will not rot. refer to example 2 above. In other words, these oranges will not be traversed by breadth first at all. In fact, the solution is also very simple. We define a variable cnt to store the number of fresh oranges in the map at the beginning. If the cnt value is still not 0 after the breadth process, it must mean that some oranges will not rot.
#include <vector>
#include <queue>
using namespace std;
typedef pair<size_t, size_t> dpoint;
class Solution
{
private:
static constexpr dpoint D[4] = {{-1, 0}, {0, -1}, {1, 0}, {0, 1}};
public:
int orangesRotting(vector<vector<int>> &grid)
{
size_t m = grid.size(), n = grid[0].size();
queue<dpoint> que;
vector<vector<int>> dist(m, vector<int>(n, -1));
int cnt = 0;
for (size_t y = 0; y < m; y++)
{
for (size_t x = 0; x < n; x++)
{
if (grid[y][x] == 2)
{
que.emplace(y, x);
dist[y][x] = 0;
}
else if (grid[y][x] == 1)
{
cnt++;
}
}
}
int ans = 0;
while (!que.empty())
{
auto [y, x] = que.front();
que.pop();
for (const auto &direction : D)
{
auto [ny, nx] = direction;
ny += y;
nx += x;
if (ny < 0 || ny >= m || nx < 0 || nx >= n || dist[ny][nx] != -1 || grid[ny][nx] == 0)
continue;
dist[ny][nx] = dist[y][x] + 1;
que.emplace(ny, nx);
if (grid[ny][nx] == 1)
{
cnt--;
ans = dist[ny][nx];
if (cnt == 0)
break;
}
}
if (cnt == 0)
break;
}
return cnt == 0 ? ans : -1;
}
};
Complexity analysis
-
Time complexity: O(mn). In the breadth first search, each land is added to the queue at most once.
-
Spatial complexity: O(mn). In the worst case, all zeros in the matrix are added to the queue; The spatial complexity of the array dist recording distance is also O(mn); The answer array is not included in the space complexity; Therefore, the spatial complexity is O(2mn)=O(mn).
Reference results
Accepted 306/306 cases passed (4 ms) Your runtime beats 92.58 % of cpp submissions Your memory usage beats 22.19 % of cpp submissions (13 MB)
Method 1 Optimization
This question and the previous one 542.01 matrix There is one thing in common, that is, in the breadth first search, the results of each round are related to the number of rounds, and an additional array is used to store which round the land is expanded. In these two questions, the land value expanded in the i round is i.
Our second question on [day 8] 116. Populate the next right node pointer for each node We encounter the hierarchical traversal of the tree, in which we need to ensure that all nodes in layer i are expanded before expanding the nodes in the next layer. Our method at that time was to record the number of elements in the initial queue at the beginning of each round of traversal, so that we can know how many nodes there are in this layer, that is, how many times the loop is extended later.
The two question as like as two peas in the tree is the same as the tree traversal. We just need to record how many nodes there are in each layer, and then define a variable level. For each outer layer, the level increases automatically. Finally, if the number cnt of fresh oranges is reduced to 0, we can directly return to level.
#include <vector>
#include <queue>
using namespace std;
typedef pair<size_t, size_t> dpoint;
class Solution
{
private:
static constexpr dpoint D[4] = {{-1, 0}, {0, -1}, {1, 0}, {0, 1}};
public:
int orangesRotting(vector<vector<int>> &grid)
{
const size_t m = grid.size(), n = grid[0].size();
queue<dpoint> que;
int cnt = 0;
for (size_t y = 0; y < m; y++)
{
for (size_t x = 0; x < n; x++)
{
if (grid[y][x] == 2)
{
que.emplace(y, x);
}
else if (grid[y][x] == 1)
{
cnt++;
}
}
}
if (cnt == 0)
return 0;
int level = 0;
while (!que.empty())
{
const size_t size = que.size();
for (size_t _ = 0; _ < size; _++)
{
const auto [y, x] = que.front();
que.pop();
for (const auto &direction : D)
{
const size_t ny = y + direction.first, nx = x + direction.second;
if (ny < 0 || ny >= m || nx < 0 || nx >= n || grid[ny][nx] != 1)
continue;
que.emplace(ny, nx);
grid[ny][nx] = 2;
cnt--;
}
}
level++;
if (cnt == 0)
return level;
}
return -1;
}
};
Complexity analysis
-
Time complexity: O(mn). In the breadth first search, each land is added to the queue at most once.
-
Spatial complexity: O(mn). It is mainly the cost of queues.
Reference results
Accepted 306/306 cases passed (4 ms) Your runtime beats 92.58 % of cpp submissions Your memory usage beats 36.37 % of cpp submissions (12.9 MB)