📢 preface

🚀 Algorithm problem 🚀

• 🌲 Punching out an algorithm problem every day is not only a learning process, but also a sharing process 😜
• 🌲 Tip: the problem-solving programming languages in this column are C# and Java
• 🌲 To maintain a state of learning every day, let's work together to become the great God of algorithm 🧐!
• 🌲 Today is the 86th day of punching out the force deduction algorithm 🎈!

🚀 Algorithm problem 🚀

🌲 Original problem example: create a string from a binary tree

You need to use preorder traversal to convert a binary tree into a string composed of parentheses and integers.

Empty nodes are represented by a pair of empty parentheses "()". And you need to omit all empty bracket pairs that do not affect the one-to-one mapping between the string and the original binary tree.

Example 1:

input: Binary tree: [1,2,3,4]
       1
     /   \
    2     3
   /    
  4     

output: "1(2(4))(3)"

explain: It would have been "1"(2(4)())(3())"，
After you omit all unnecessary empty parenthesis pairs,
It will be "1"(2(4))(3)". 

Example 2:

input: Binary tree: [1,2,3,null,4]
       1
     /   \
    2     3
     \  
      4 

output: "1(2()(4))(3)"

explain: Similar to the first example,
Except that we cannot omit the first pair of parentheses to interrupt the one-to-one mapping between input and output.

Tips:

• The length range of both lists is within [1, 1000].
• The length of the strings in both lists will be in the range of [1, 30].
• The subscript starts at 0 and the length of the list minus 1.
• Neither list has duplicate elements.

🌻 C# method: recursive traversal

Recursive traversal. When an empty node is encountered, use () instead

code:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int x) { val = x; }
 * }
 */
public class Solution {
           StringBuilder str = new StringBuilder();
        public string Tree2str(TreeNode t)
        {
           
            if (t!=null)
            {
                def(t);
            }
            return str.ToString();
        }
        public void def(TreeNode root)
        {
            if (root==null)
            {
                return;
            }
             str.Append(root.val);
            if (root.left!=null|| root.right != null)
            {
                str.Append('(');
                def(root.left);
                str.Append(')');
            }
            if (root.right != null)
            {
                str.Append('(');
                def(root.right);
                str.Append(')');
            }            
        }

}

results of enforcement

adopt
 Execution time: 92 ms，At all C# Defeated 92.50% of users in submission
 Memory consumption: 40.9 MB，At all C# Beat 84.90% of users in submission

🌻 Java methods: recursion

Train of thought analysis
You can use the recursive method to get the preorder traversal of the binary tree. During recursion, we need to add additional parentheses according to the topic description. There are four cases as follows:

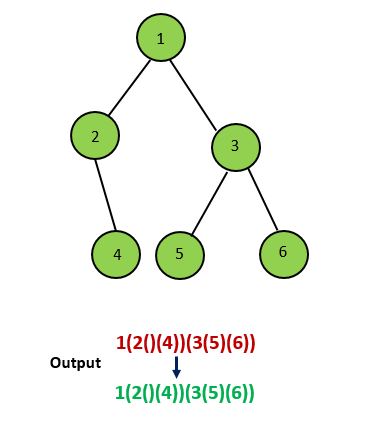
• If the current node has two children, we need to add a layer of parentheses outside the results of the two children when recursing;

• If the current node has no children, we do not need to add any parentheses after the node;
  

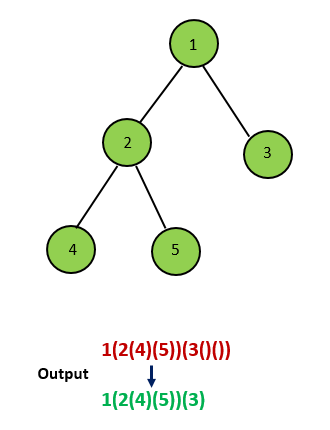
• If the current node has only the left child, when recursing, we only need to add a layer of parentheses to the result of the left child, rather than any parentheses to the right child;
  

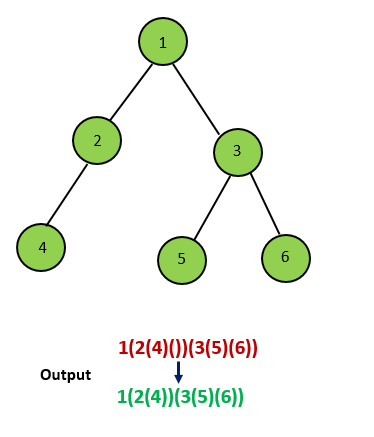
• If the current node has only the right child, we need to add a layer of empty parentheses () to indicate that the left child is empty, then recurse the right child, and add a layer of parentheses to the result.

After considering the above four cases, we can get the final string.

code:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public class Solution {
    public String tree2str(TreeNode t) {
        if(t==null)
            return "";
        if(t.left==null && t.right==null)
            return t.val+"";
        if(t.right==null)
            return t.val+"("+tree2str(t.left)+")";
        return t.val+"("+tree2str(t.left)+")("+tree2str(t.right)+")";   
    }
}

results of enforcement

adopt
 Execution time: 15 ms，At all Java  Defeated 44 in submission.08%User
 Memory consumption: 40.1 MB，At all Java Defeated 24 in submission.40%User

Complexity analysis

Time complexity: O( n )
Space complexity: O(n) 

💬 summary

• Today is the 86th day of punching out the force deduction algorithm!
• This paper uses C# and Java programming languages to solve problems
• Some methods are also written by Likou God, and they are also shared while learning. Thanks again to the algorithm bosses
• That's the end of today's algorithm sharing. See you tomorrow!