4, Notes on data structure of postgraduate entrance examination -- basic knowledge of stack and queue (understanding of stack and queue, confusing points, familiar code)

Posted by parag on Tue, 30 Nov 2021 15:58:55 +0100

1, Refining the concept of stack and queue

  • Both stack and queue are linear tables with limited operation, which are linear structures. The logical structure is the same.
  • The stack is summarized as LIFO (last in, first out); The queue is summarized as FIFO (first in first out)
  • For the stack, n different elements, the number of different permutations of stack elements (as follows)

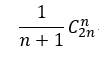
2, Basic operation of stack (code to be memorized)

2.1 stack structure

#define MaxSize 50
typedef struct{
	ElemType data[MaxSize];	//Store elements in the stack
	int top;				//Stack top pointer
}

2.2 initialization stack

void InitStack(SqStack &S){
	S.top=-1;		//The initialization stack top pointer is - 1
}

2.3 judge whether the stack is empty

bool StackEmpty(SqStack &S){
	if(S.top==-1)	//Stack empty
		return true;
	else
		return false;
}

2.4 stacking

bool Push(SqStack &S,ElemType x){
	if(S.top == MaxSize -1)		//Stack full, error reported
		return false;
	S.data[++S.top] = x;		//This is the core
	return true;
	//
There may be a little change in this code, and the exam may change the initial S.top Set to 0; In that case,
}

2.5 out of stack

bool Pop(SqStack &S,ElemType &x){
	if(S.top == -1)		//Stack empty, error reported
		return false;
	x=S.data[S.top--];	//This paragraph is the core
	return true;
}

2.6 reading stack top elements

bool GetTop(SqStack &S,ElemType &x){
	if(S.top == -1)		//Stack empty error
		return false;
	x=S.data[S.top];		
	return true;
}

2.7 changing initial conditions (flexible)

Some problems change the pointer from - 1 to 0. As shown below

At this time, the key codes of initialization, stack entry and stack exit need to be changed,

  • Initialization: S.top=0
  • Stack entry: S.data[top++] =x;
  • Stack out: x = s.data [-- s.top];

3, Shared stack and chain stack (just understand)

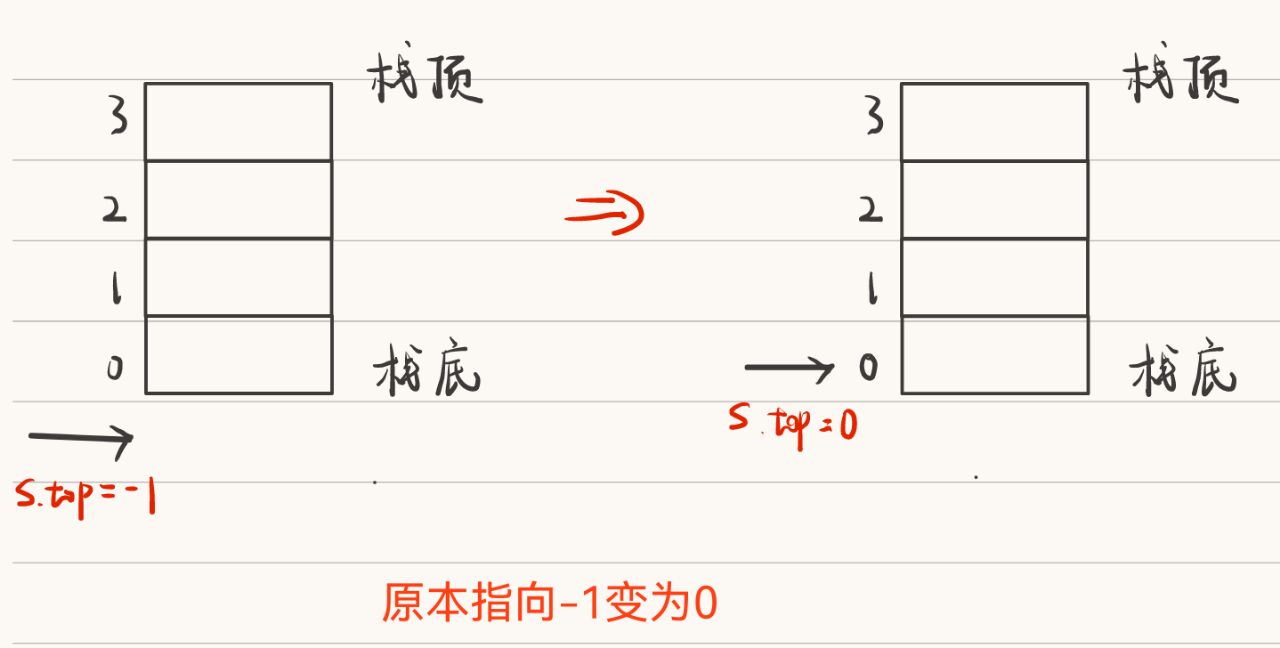
3.1 shared stack definition

  • By two pointers, the top of the two stacks extends to the middle in order to make better use of the storage space
  • top0=-1, indicating that the stack 0 from bottom to top is empty;
  • top1=maxSize, indicating that stack 1 from top to bottom is empty;
  • When top1-top0=1, both stacks are full.
  • The storage time complexity is O(1);

3.2 shared stack structure

#define MaxSize 10
typedef struct{
	ElemType data[MaxSize];
	int top0;	//Stack top pointer 0
	int top1;	//Stack top pointer 1
}

3.3 shared stack initialization

void InitStack(ShStack &S){
	S.top0 = -1;
	S.top1 =MaxSize;
}

3.4 chain stack concept

  • In fact, it is a single linked list. All inserted elements are carried out at the head node. You can see the single linked list in the previous article
  • Advantages: there is no stack overflow and infinite extension. It is convenient for multiple stacks to share storage space and improve efficiency

3.5 chain stack structure

typedef struct LinkNode{
	ElemType data;	//Data domain
	struct LinkNode *next;//Pointer field
} *LiStack;

4, Queue definition

  • A linear table with limited operation. It is allowed to insert (queue) at one end of the table and delete (dequeue) at the other end.
  • fifo. FIFO
  • front header, rear footer

5, Queue sequential storage structure

define MaxSize 50
typedef struct{
	ElemType data[MaxSize];
	int front,rear;
}SqQueue;

6, Sequential queue to cyclic queue

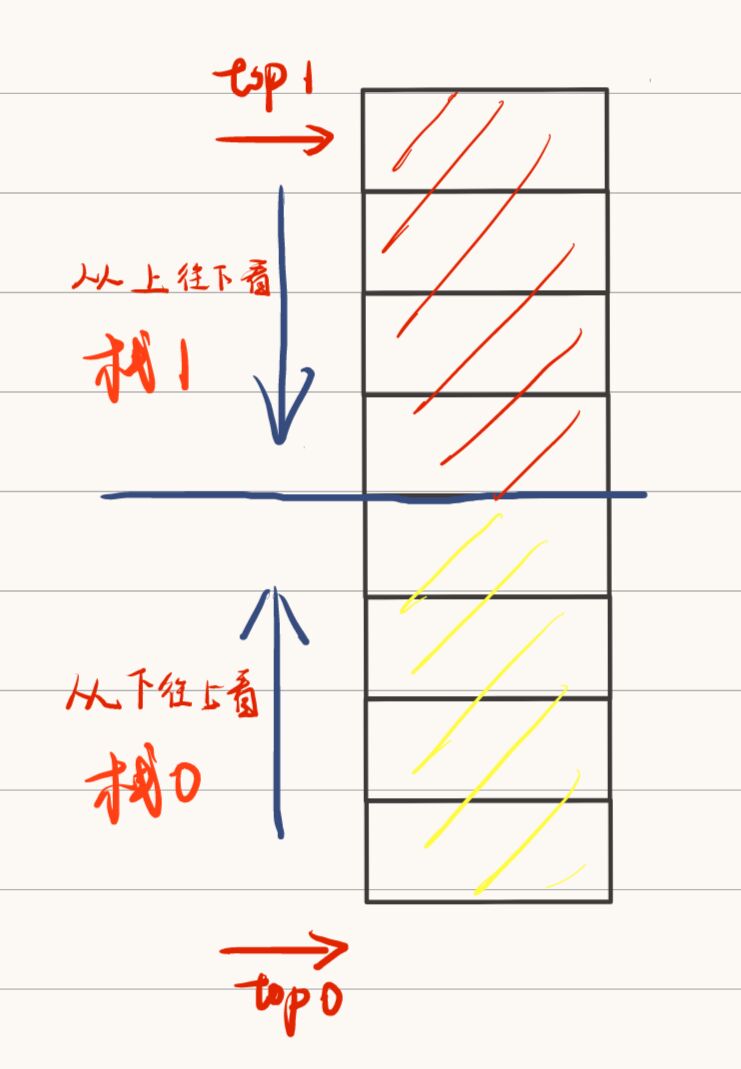
The general sequence queue is as follows

  • Queue empty status Q.front == Q.rear=0
  • Team entry status: add one at the end of the team
  • Out of line status: add one to the head

However, the queue is a linear table. Moving up all the time will lead to pointer out of bounds, so the queue is generally imagined as a ring, so the above situation will not occur.

Therefore, in general exams, the queues discussed are circular queues, which must be understood. Otherwise, I don't know how to suddenly come to the circular queue

7, Basic operation of circular queue (code to be memorized)

7.1 cycle queue initialization

void InitQueue(SqQueue &Q){
	Q.rear = Q.front = 0;		//Initializes the queue head and tail pointers
}

7.2 circular queue empty judgment

bool isEmpty(SqQueue Q){
	if(Q.rear == Q.front)
		return true;
	else
		return false;
}

7.3 cyclic queue entry

bool EnQueue(SqQueue &Q,Elemtype x){
	if((Q.rear+1)%MaxSize==Q.front)	//The queue is full. Remember this
		return false;
	Q.data[Q.rear] = x;
	Q.rear=(Q.rear + 1) %MaxSize;
	return true;
}

7.4 cyclic queue exit

bool DeQueue(SqQueue &Q,ElemType &x){
	if(Q.rear == Q.front)	//Team empty error reporting
		return false;
	x = Q.data[Q.front];
	Q.front = (Q.front+1)%MaxSize;	//Team leader pointer + 1
	return true;

}

7.5 other common test operations

  • Team full: (Q.rear +1)% MaxSize==Q.front
  • Number of elements in the queue: (Q.rear -Q.front+ MaxSize)% MaxSize
  • Queue (add element) pointer change: Q.front = (Q.front+1)% MaxSize
  • Out of queue (delete element) pointer change: Q.rear = (Q.rear+1)% MaxSize

7.6 multiple choice test method 1

  • Often give an array, and then give the current values of real and front to calculate the total number of elements in the queue
  • Use the above formula to calculate

7.7 multiple choice test method 2

  • An array that gives the initial rear and front values. What are the rear and front values after deleting n elements and inserting n elements
  • Using the above formula, both front and rear are + 1. It's just that the number of deleted elements plus front and the number of increased elements plus rear.
  • Second, don't forget% MaxSize

6, Different ways for circular queue to judge empty and full

6.1 mode I

  • This method is also the most default method, sacrificing an element for judgment.
  • structural morphology
#define MaxSize 10
typedef struct{
	ElemType data[MaxSize];
	int front,rear;
}SqQueue;
  • Initialization: Q.rear=Q.front=0
  • Team empty: Q.rear == Q.front
  • Queue full: Q.rear = (Q.rear+1)% MaxSize

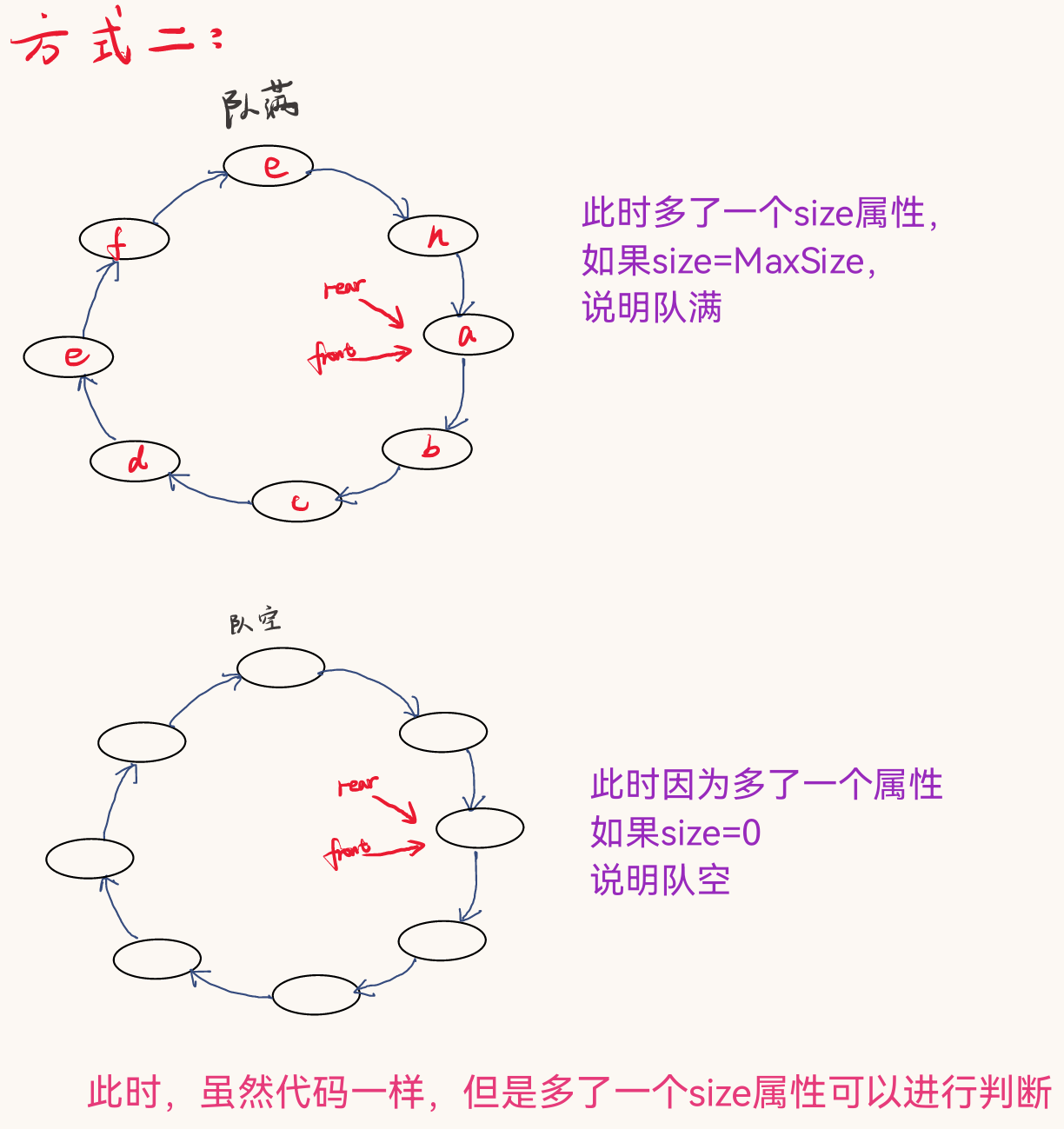
6.2 mode II

  • During the exam, I just want to fill in the wasted part of method 1
  • structural morphology
#define MaxSize 10
typedef struct{
	ElemType data[MaxSize];
	int front,rear;
	int size;	//Current queue length
}SqQueue;
  • Initialization: ① rear = front = 0; ② int size=0
  • Team empty: ① front == rear; ②size ==0
  • Team full: ① front == rear; ②size ==MaxSize

6.3 mode III

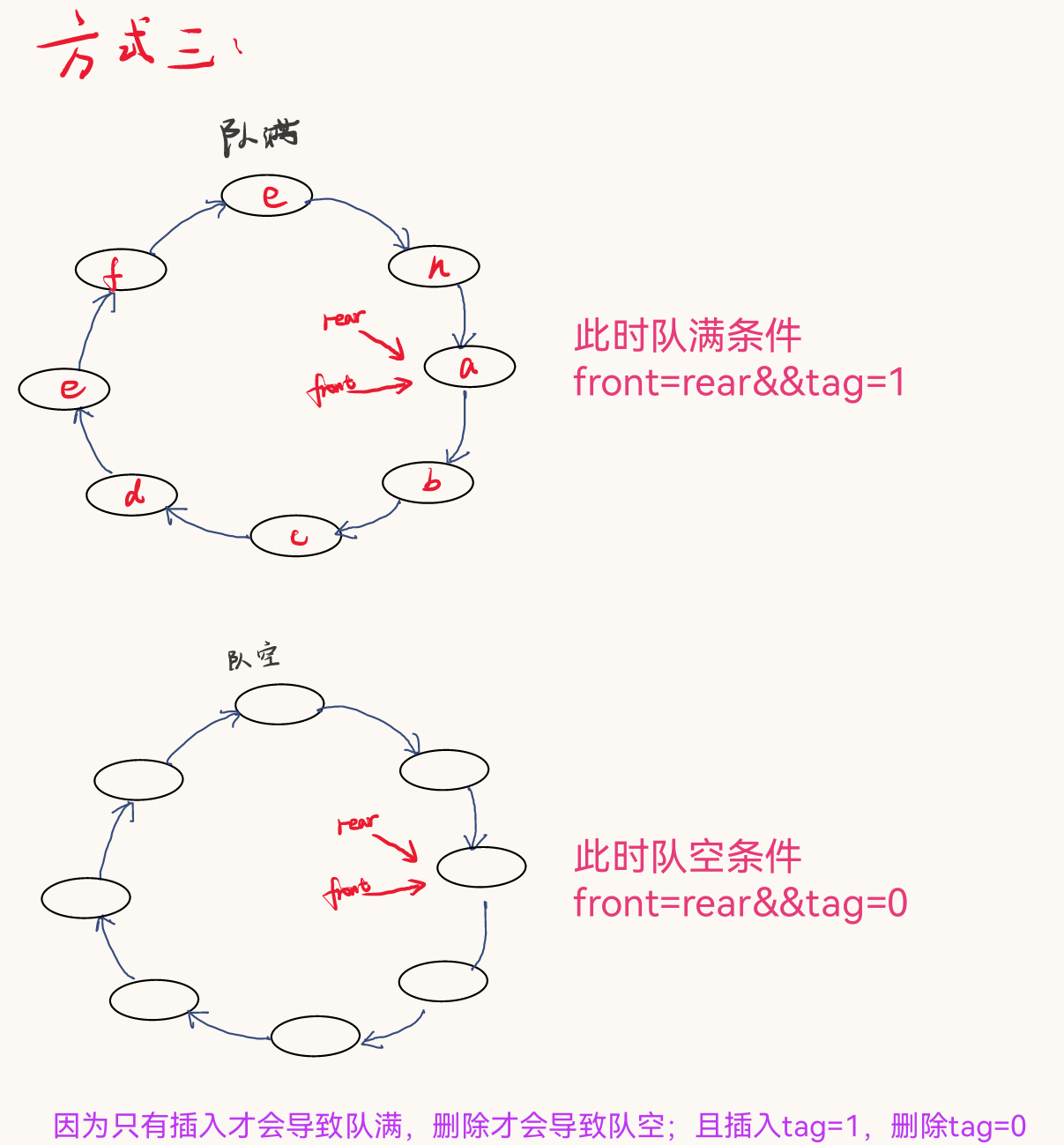
  • When defining a structure, define a label. tag= 0 means deletion. tag=1 means insertion
  • structural morphology
#define MaxSize 
typedef struct{
	ElemType data[MaxSize];
	int front,rear;
	int tag;	//Last delete / insert delete: 0 insert: 1
}SqQueue;
  • Initialization: front =rear=0;tag==0
  • Queue empty: front = = rear & & tag = = 0
  • Team full: front = = rear & & tag = = 1

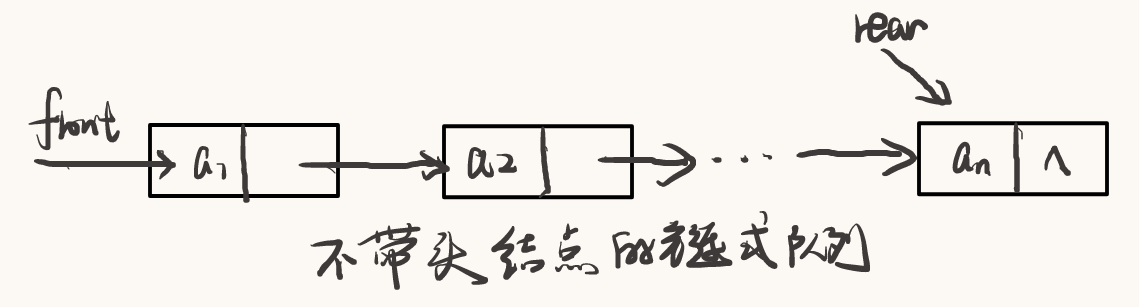
7, Definition and structure of queue chain storage

In fact, it is a single linked list with both team head pointer and team tail pointer. As shown in the figure

Its structure is (understand)

typedef struct{
	ElemType data;
	struct LinkNode *next;
}LinkNode;
typedef struct{
	LinkNode *front,*rear;
}LinkQueue;

8, Basic operation of chain queue (similar to sequential queue)

8.1 initialization

void InitQueue(LinkQueue &Q){
	Q.rear = Q.front = (LinkNode *)malloc(sizeof(LinkNode));		//Create header node
	Q.front->next =NULL;//Initial null
}

8.2 air judgment

bool isEmpty(LinkQueue Q){
	if(Q.rear == Q.front)
		return true;
	else
		return false;
}

8.3 joining the team

void EnQueue(LinkQueue &Q,Elemtype x){
	LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode));
	s->data = x;s->next =NULL;//Create a new node and insert it at the end of the chain
	Q.rear->next = s;
	Q.rear=s;
}

8.4 departure

bool DeQueue(LinkQueue &Q,ElemType &x){
	if(Q.rear == Q.front)	//Team empty error reporting
		return false;
	LinkNode *p=Q.front->next;
	x = p->data;
	Q.front->next = p->next;
	if(Q.rear == p)
		Q.rear = Q.front; //If there is only one node in the original queue, it will become empty after deletion
	free(p)
	return true;
}

9, Double ended queue

This part will test multiple-choice questions, understand its function, and be able to calculate and simulate by hand
Both ends are allowed to enter and leave the team. The logical structure is still linear. As shown in the figure.

This place can do several topics, the key is to pay attention to logical analysis. for instance

A queue allows queue in operations at both ends, but only queue out operations at one end. If the element abcde enters the queue in turn, then exit the queue. Impossible sequence. A. bacde B. dbace C. dbcae D.ecbad

Stack and queue is not very difficult, test some simple code. Not much. And the calculation of multiple-choice questions, we must clarify their differences, first in first out, first in first out. Attention logic
Stack and queue are mainly difficult in the next article, the application of stack and queue.

Topics: C data structure queue stack

Hot Topics

©2024 Programmer Think