Write in front
I finished it the day before yesterday Fuzzy clustering based on transitive closure Today, I'm going to write "genetic algorithm for unconstrained single objective optimization problem". Yesterday, I played with npy all afternoon, went to Qi Baishi art college to see the painting exhibition, watched the sunset at the highest place, and kissed before sunset.
Experimental topic
Solving unconstrained single objective optimization problem by genetic algorithm
Experimental purpose
Understand the principle of genetic algorithm, master the basic solving steps of genetic algorithm, including selection, crossover and mutation, and learn to use genetic algorithm to solve unconstrained single objective optimization problems.
background knowledge
Genetic algorithm is a random search method based on the genetic mechanism of natural selection and survival of the fittest in the biological world. Genetic algorithm simulates the phenomena of heredity, mutation, natural selection and hybridization in evolutionary biology. It is a kind of evolutionary algorithm. For an optimization problem, the population of the abstract representation (also known as chromosome) of a certain number of candidate solutions (each candidate solution is called an individual) evolves in a better direction. Through continuous reproduction from generation to generation, the population converges to the most suitable environment, so as to obtain the optimal solution of the problem. Evolution begins with a completely randomly selected individual population, which reproduces and evolves from generation to generation. In each generation, the fitness of each individual of the whole population is evaluated. Multiple individuals are randomly selected from the current population (based on their fitness), and a new population is generated through natural selection, survival of the fittest and mutation. The population will become the current population in the next iteration of the algorithm. Traditionally, the solution is generally expressed in binary (a string of 0 and 1). The main feature of genetic algorithm is to operate the structural object directly, without the limitation of function derivation, continuity and single peak; It has inherent hidden closed parallelism and better global optimization ability; The probabilistic optimization method can automatically obtain and guide the optimization search, adaptively adjust the search direction, and there is no need to determine the rules. Genetic algorithm has been widely used in combinatorial optimization, machine learning, signal processing, adaptive control and artificial intelligence. It has become a key technology in modern intelligent computing.
Key terms:
(1) Individuals: the objects processed in genetic algorithm are called individuals. Individuals can usually contain the coding representation of solutions, fitness values and other components, so they can be regarded as a structural whole. Among them, the main component is coding.
(2) Population: a collection of individuals is called a population.
(3) Bit string: the coded representation of the solution is called bit string. The coded representation of the solution can be 0, 1 binary string, 0 ~ 9 decimal number string or other forms of string, which can be called string or string for short. The bit string corresponds to the chromosome. In the description of genetic algorithm, the concepts of bit string and chromosome are often used indiscriminately. Relationship between bit string / chromosome and individual: bit string / chromosome is generally an individual component, and an individual can also contain components such as moderate value. Individuals, chromosomes, bit strings or strings can sometimes be used indiscriminately in genetic algorithms.
(4) Population scale: also known as population size, it refers to the number of individuals in a population.
(5) Gene: each bit or element in the bit string is collectively referred to as a gene. Genes reflect individual characteristics. Different genes at the same locus may lead to different individual characteristics. Genes correspond to genetic material units in genetics. In DNA sequence representation, genetic material units are also represented by specific codes. The concept of coding is extended in genetic algorithm. The feasible solution can be expressed by 0, 1 binary, 0 ~ 9 ten numbers and other forms of coding. For example, if there is a string S=1011 under the binary coding of 0 and 1, the four elements 1, 0, 1 and 1 are called genes respectively. Genes and loci can also be used indiscriminately in genetic algorithms.
(6) Fitness: the degree to which an individual adapts to the environment is called fitness. In order to reflect the adaptability of chromosomes, a function that can measure each chromosome is usually introduced, which is called fitness function.
(7) Selection: the operation of selecting an individual in the whole population or part of the population.
(8) Crossover: the exchange of one or more gene segments corresponding to two individuals.
(9) Mutation: the value of a gene on an individual bit string changes. For example, under the string representation of 0 and 1, the value of a bit changes from 0 to 1, or from 1 to 0.
The basic flow of genetic algorithm is as follows:
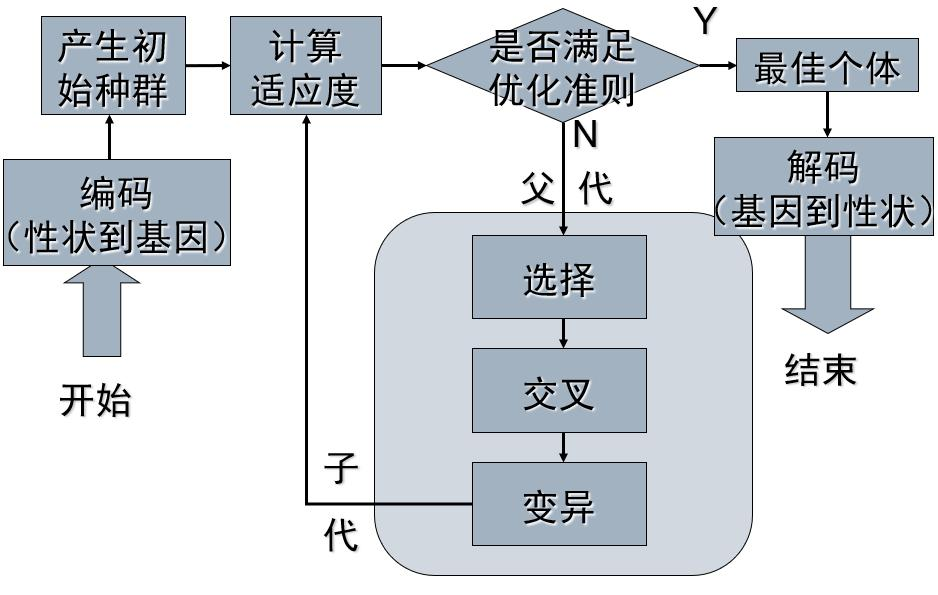
This case is intended to illustrate how to use genetic algorithm to solve unconstrained single objective optimization problem, that is, to find univariate function:
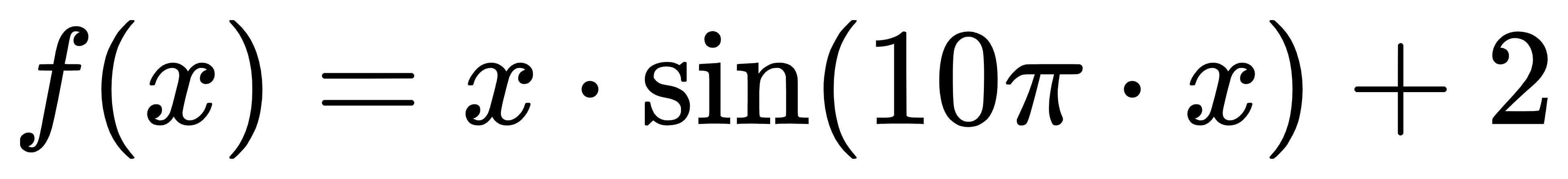
The maximum value on the interval [- 1, 2]. The function image is as follows:
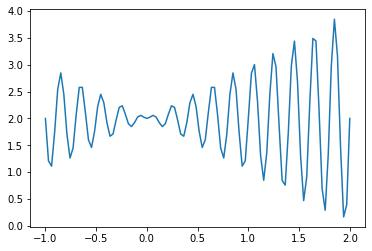
It can be seen from the image that the function has many maxima and minima in the interval [- 1,2]. For the problem of finding its maximum or minimum, many single point optimization methods (gradient descent, etc.) are not suitable. In this case, genetic algorithm can be considered..
Sample code
import numpy as np
import matplotlib.pyplot as plt
def fun(x):
return x * np.sin(10*np.pi*x) + 2
Xs = np.linspace(-1, 2, 100)
np.random.seed(0) # Make the random number seed = 0 to ensure that the same random number is obtained each time
# Initialize original population
population = np.random.uniform(-1, 2, 10) # Generate 10 floating-point numbers on [- 1,2) with uniform distribution as the initial population
for pop, fit in zip(population, fun(population)):
print("x=%5.2f, fit=%.2f" % (pop, fit))
plt.plot(Xs, fun(Xs))
plt.plot(population, fun(population), '*')
plt.show()
def encode(population, _min=-1, _max=2, scale=2**18, binary_len=18): # population must be of float type, otherwise the precision cannot be guaranteed
# Standardize so that all data is between 0 and 1, multiply by scale to make the data spacing larger for binary representation
normalized_data = (population-_min) / (_max-_min) * scale
# Convert to binary encoding
binary_data = np.array([np.binary_repr(x, width=binary_len)
for x in normalized_data.astype(int)])
return binary_data
chroms = encode(population) # Chromosome English
for pop, chrom, fit in zip(population, chroms, fun(population)):
print("x=%.2f, chrom=%s, fit=%.2f" % (pop, chrom, fit))
def decode(popular_gene, _min=-1, _max=2, scale=2**18): # First convert x from binary to decimal, indicating which copy this is
# Multiply each length (length / copies) and add the starting point to finally convert a binary number into x-axis coordinates
return np.array([(int(x, base=2)/scale*3)+_min for x in popular_gene])
fitness = fun(decode(chroms))
for pop, chrom, dechrom, fit in zip(population, chroms, decode(chroms), fitness):
print("x=%5.2f, chrom=%s, dechrom=%.2f, fit=%.2f" %
(pop, chrom, dechrom, fit))
fitness = fitness - fitness.min() + 0.000001 # Make sure all are positive
print(fitness)
def Select_Crossover(chroms, fitness, prob=0.6): # Selection and crossover
probs = fitness/np.sum(fitness) # Probability of individual selection
probs_cum = np.cumsum(probs) # Probability cumulative distribution
each_rand = np.random.uniform(size=len(fitness)) # Get 10 random numbers, between 0 and 1
# Roulette, select a new gene code according to random probability
# For each random number in each_rand, find the chromosome in the roulette
newX = np.array([chroms[np.where(probs_cum > rand)[0][0]]
for rand in each_rand])
# Reproduction, random pairing (probability 0.6)
# How does the number 6 come from? According to the genetic algorithm, suppose there are 10 numbers, the crossover probability is 0.6, 0 and 1, 2 and 3... 8 and 9, and each group throws a number between 0 and 1
# If this number is less than 0.6, there should be three groups of crossover on average, that is, six chromosomes should be crossed
pairs = np.random.permutation(
int(len(newX)*prob//2 * 2). Reshape (- 1, 2) # generates 6 random numbers. Arrange them randomly and divide them into two columns
center = len(newX[0])//2 # the simplest central crossing method is adopted
for i, j in pairs:
# Cross in the middle
x, y = newX[i], newX[j]
newX[i] = x[:center] + y[center:] # The elements of newX are strings, which can be spliced directly with the + sign
newX[j] = y[:center] + x[center:]
return newX
chroms = Select_Crossover(chroms, fitness)
dechroms = decode(chroms)
fitness = fun(dechroms)
for gene, dec, fit in zip(chroms, dechroms, fitness):
print("chrom=%s, dec=%5.2f, fit=%.2f" % (gene, dec, fit))
# Compare the results after selection and crossover
fig, (axs1, axs2) = plt.subplots(1, 2, figsize=(14, 5))
axs1.plot(Xs, fun(Xs))
axs1.plot(population, fun(population), 'o')
axs2.plot(Xs, fun(Xs))
axs2.plot(dechroms, fitness, '*')
plt.show()
# Input an original population 1 and output a variant population 2. The colon in the function parameter is the type recommender of the parameter, telling the programmer the type of the argument you want to pass in. The arrow followed by the function is the type recommender of the return value of the function, which is used to indicate what type the value returned by the function is.
def Mutate(chroms: np.array):
prob = 0.1 # Probability of variation
clen = len(chroms[0]) # Chrome [0] = "111101101 000010110" length of string = 18
m = {'0': '1', '1': '0'} # m is a dictionary, including two pairs: the first pair 0 is key and 1 is value; The second pair of 1 is key and 0 is value
newchroms = [] # New species after storage variation
each_prob = np.random.uniform(size=len(chroms)) # Random 10 numbers
for i, chrom in enumerate(chroms): # The function of enumerate is to generate the whole i
if each_prob[i] < prob: # If you want to mutate (the use of i is here)
pos = np.random.randint(clen) # Find a random location from 18 locations, assuming 7
# 0 ~ 6 remain unchanged, 8 ~ 17 remain unchanged, and only turn No. 7, that is, 0 is changed to 1, and 1 is changed to 0. Note that the characters in chrom e are either 1 or 0
chrom = chrom[:pos] + m[chrom[pos]] + chrom[pos+1:]
newchroms.append(chrom) # Whether the if is true or not, this element of chrome is added to new chrome
return np.array(newchroms) # Returns the mutated population
newchroms = Mutate(chroms)
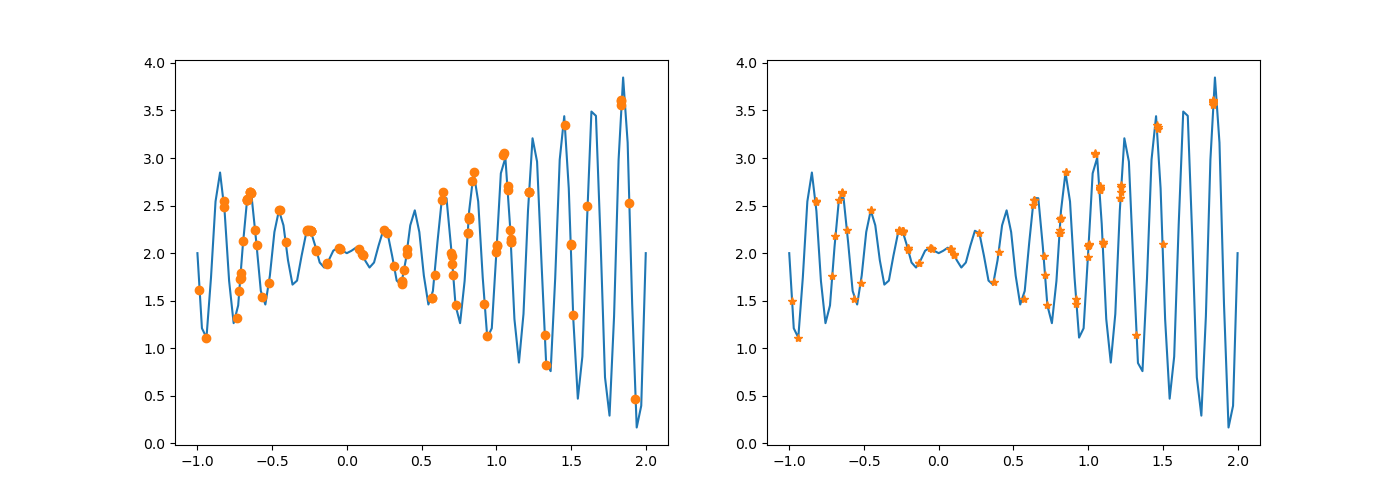
def DrawTwoChroms(chroms1, chroms2, fitfun): # Draw two pictures, the old population on the left and the new population on the right. Observe the two parallel pictures to see if there is any difference
Xs = np.linspace(-1, 2, 100)
fig, (axs1, axs2) = plt.subplots(1, 2, figsize=(14, 5))
dechroms = decode(chroms1)
fitness = fitfun(dechroms)
axs1.plot(Xs, fitfun(Xs))
axs1.plot(dechroms, fitness, 'o')
dechroms = decode(chroms2)
fitness = fitfun(dechroms)
axs2.plot(Xs, fitfun(Xs))
axs2.plot(dechroms, fitness, '*')
plt.show()
# Compare the results before and after the mutation
DrawTwoChroms(chroms, newchroms, fun)
# The above code is only a round of execution, which is repeated here
np.random.seed(0) #
population = np.random.uniform(-1, 2, 100) # Find more this time
chroms = encode(population)
for i in range(1000):
fitness = fun(decode(chroms))
fitness = fitness - fitness.min() + 0.000001 # Make sure all are positive
newchroms = Mutate(Select_Crossover(chroms, fitness))
if i % 300 == 1:
DrawTwoChroms(chroms, newchroms, fun)
chroms = newchroms
DrawTwoChroms(chroms, newchroms, fun)
Experimental content
Run and understand the sample code and answer the following questions:
1) What is the semantics of line 64 of the code? What do two [0] represent? Finally, how many elements does newX have?
newX = np.array([chroms[np.where(probs_cum > rand)[0][0]] for rand in each_rand])
2) What is the semantics of line 70 of the code? Why divide by two and multiply by two? What does - 1 in reshape mean?
pairs = np.random.permutation( int(len(newX)*prob//2 * 2). Reshape (- 1, 2) # generates 6 random numbers, which are randomly arranged and divided into two columns
3) Please describe in detail how the mutation is implemented in combination with the content of the Mutate function.
4) Change line 145 of the code to newchrome = select_ Crossover (chroms, fitness), that is, variation is no longer performed. What is the difference between the execution results and why this change occurs?
5) Roulette allows individuals to be selected according to probability. For individuals with the highest fitness, although the probability of selection is high, they may still be eliminated, so as to lose the current best individuals in the process of evolution. An improvement scheme is to let the individual with the highest fitness not participate in the selection, but directly enter the next round (direct promotion). This scheme is called elitist selection. Please modify the code of the Select section to realize this idea.
6) [optional] please refer to the example code to realize example 2.6.1 of textbook P57, that is, use genetic algorithm to solve the maximum value of the following binary function.
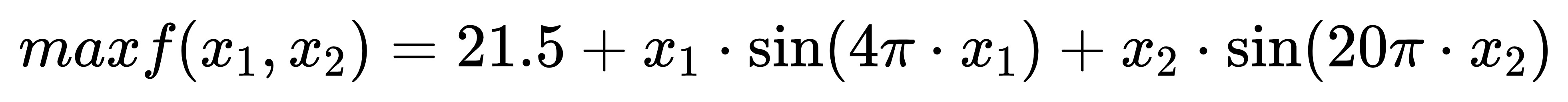
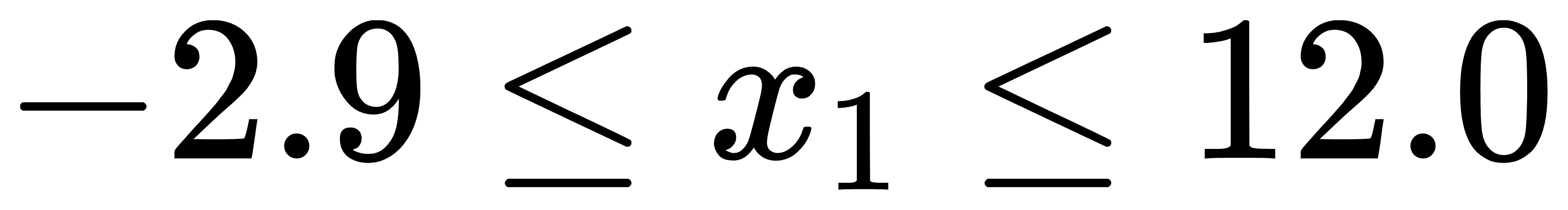
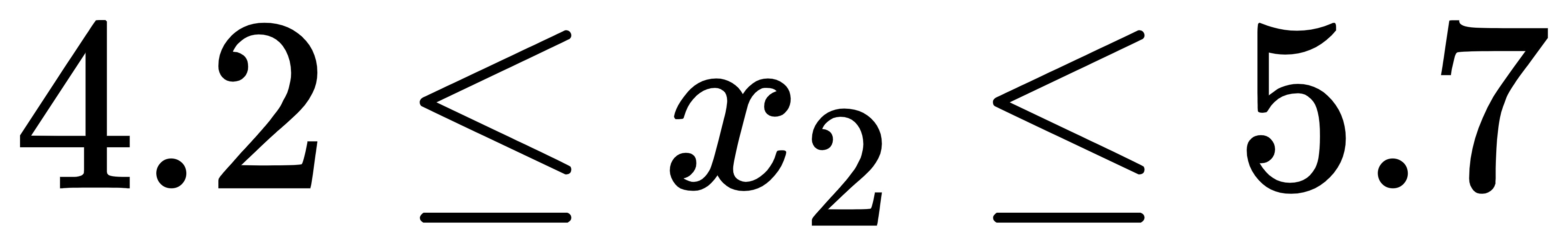
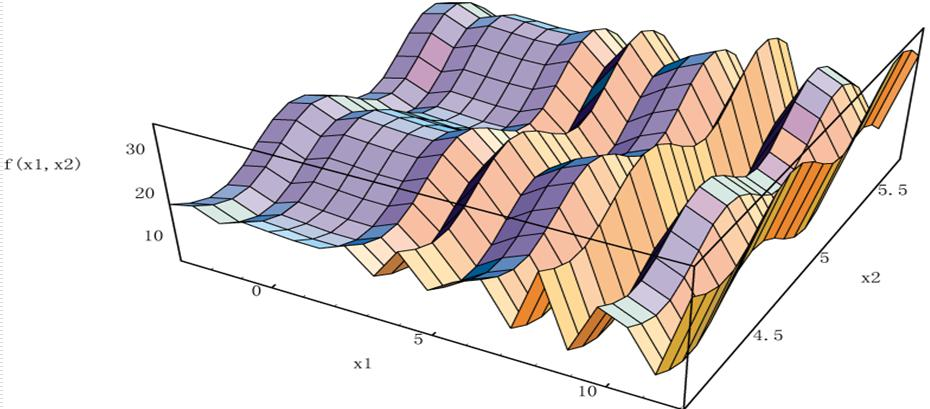
Experimental results and analysis
First question
1) What is the semantics of line 64 of the code? What do two [0] represent? Finally, how many elements does newX have?
newX = np.array([chroms[np.where(probs_cum > rand)[0][0]] for rand in each_rand])
After splitting, the results are as follows:

The code above is equal to
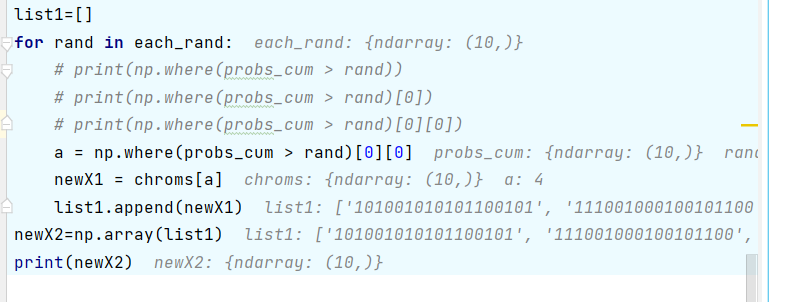
Where for in [] is a list generating expression and returns a list. The first [0] represents the row index of the array in tuple tuple generated by np.where()[0] is the first array in tuple. Since there is only one array in this example, only one one-dimensional array is returned, and the second [0] is the first element of the one-dimensional array.
Finally, newX has a total of 100 elements.
Second question
2) What is the semantics of line 70 of the code? Why divide by two and multiply by two? What does - 1 in reshape mean?
pairs = np.random.permutation( int(len(newX)*prob//2 * 2). Reshape (- 1, 2) # generates 6 random numbers, which are randomly arranged and divided into two columns
-
Randomly generate 6 numbers between [0,5] and arrange them into a two-dimensional array with a shape of (3,2).
-
newX has ten elements, which can be understood as ten chromosomes. Because of random pairing, we group chromosomes in pairs, so / / 2 indicates that they are divided into five groups. After being divided into five groups, multiply by the random pairing probability to get a total of three groups of chromosomes to be paired. Pairing is the behavior between a single chromosome and another single chromosome, so we have to multiply by 2, indicating that a total of six chromosomes need to be paired.
-
- 1 in reshape means that the number of rows of the array is automatically calculated by the number of columns. The new shape attribute should be matched with the original one. If it is equal to - 1, Numpy will calculate another shape attribute value of the array according to the remaining dimensions.
Question 3
3) Please describe in detail how the mutation is implemented in combination with the content of the Mutate function.
def Mutate(chroms: np.array):
prob = 0.1 # Probability of variation
clen = len(chroms[0]) # Chrome [0] = "111101101 000010110" length of string = 18
m = {'0': '1', '1': '0'} # m is a dictionary, including two pairs: the first pair 0 is key and 1 is value; The second pair of 1 is key and 0 is value
newchroms = [] # New species after storage variation
each_prob = np.random.uniform(size=len(chroms)) # Random 10 numbers
for i, chrom in enumerate(chroms): # The function of enumerate is to generate the whole i
if each_prob[i] < prob: # If you want to mutate (the use of i is here)
pos = np.random.randint(clen) # Find a random location from 18 locations, assuming 7
# 0 ~ 6 remain unchanged, 8 ~ 17 remain unchanged, and only turn No. 7, that is, 0 is changed to 1, and 1 is changed to 0. Note that the characters in chrom e are either 1 or 0
chrom = chrom[:pos] + m[chrom[pos]] + chrom[pos+1:]
newchroms.append(chrom) # Whether the if is true or not, this element of chrome is added to new chrome
return np.array(newchroms) # Returns the mutated population
- Firstly, the mutation probability and the length of a single chromosome (binary digits) are obtained, and then the dictionary is used to store the two cases of mutation.
- New chroms is an array that stores new populations after mutation.
- Through each_prob calculates the random variation probability of each chromosome
- Traverse the chromosome. If the random mutation probability is lower than the mutation probability, mutation occurs
- Mutation occurs. By calculating pos, a position mutation is randomly found from the chromosome, that is, a mutation occurs at a bit of binary number
- No matter whether the chromosome is mutated or not, the chromosome is added to the new population (both mutated and well aged)
- Returns the entire new population
Before modification:
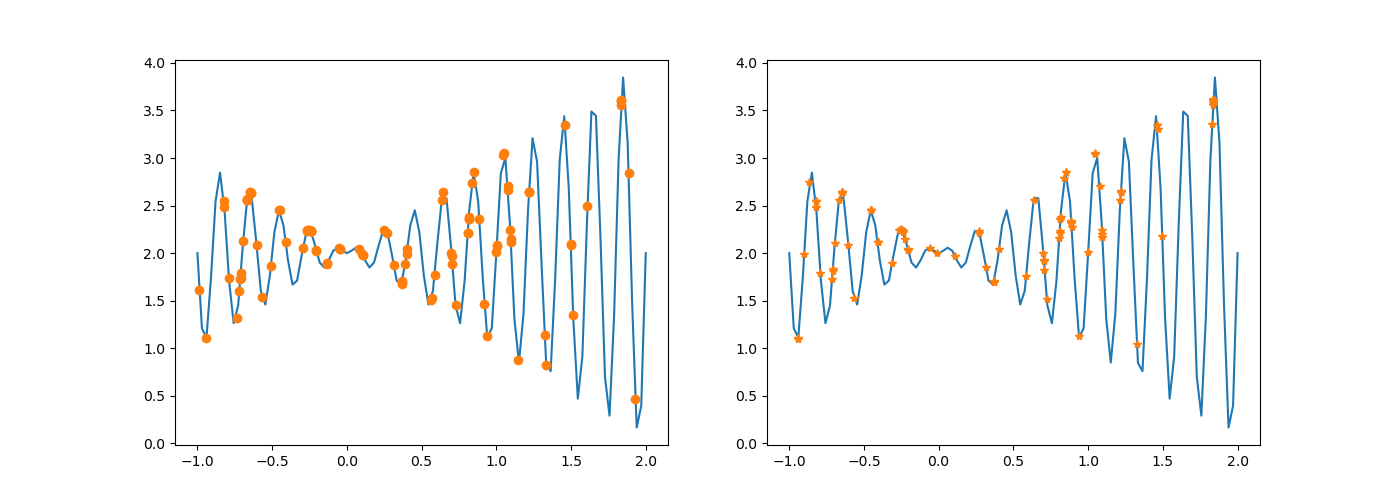
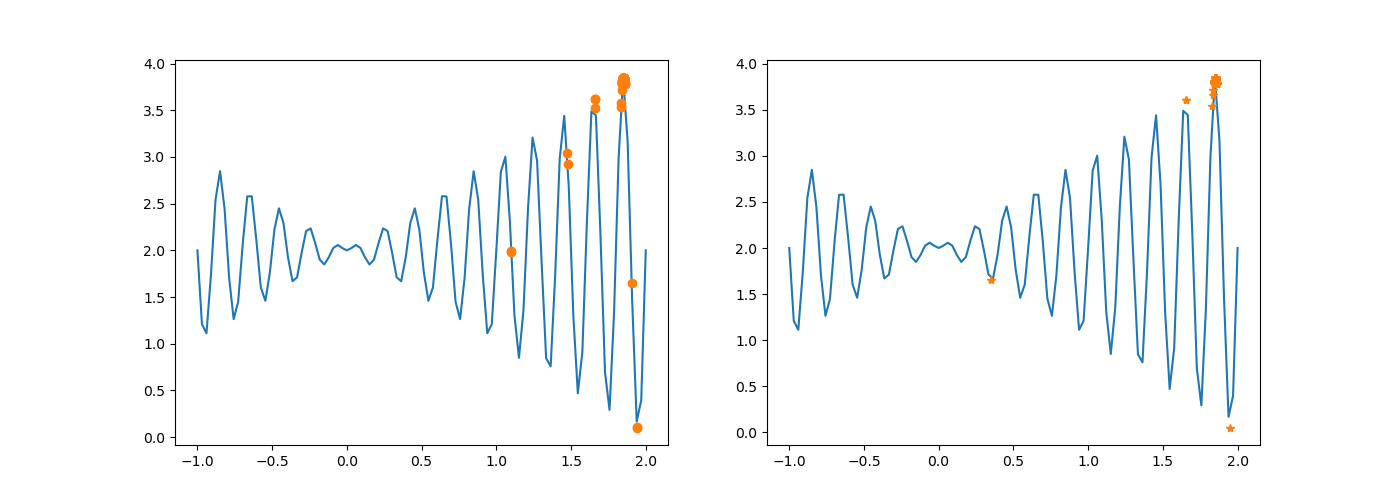
After modification:

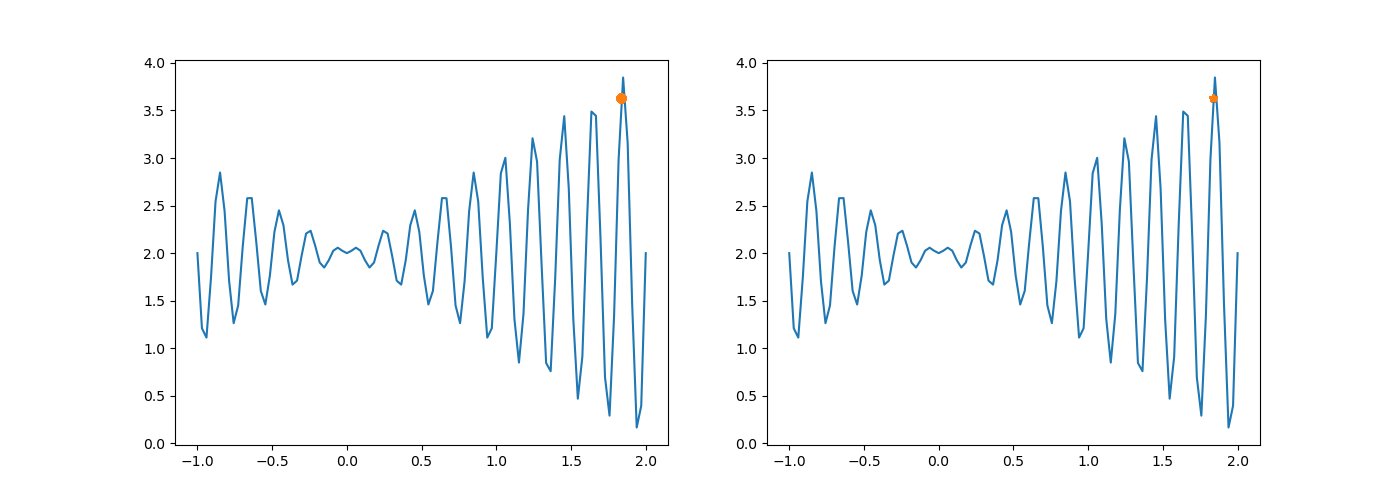
The execution result changes as above.
After chromosome crossing, no variation occurs. Without one mutation, the difference between the new population and the original population is smaller in probability.
Question 5
5) Roulette allows individuals to be selected according to probability. For individuals with the highest fitness, although the probability of selection is high, they may still be eliminated, so as to lose the current best individuals in the process of evolution. An improvement scheme is to let the individual with the highest fitness not participate in the selection, but directly enter the next round (direct promotion). This scheme is called elitist selection. Please modify the code of the Select section to realize this idea.
def Select_Crossover(chroms, fitness, prob=0.6): # Selection and crossover
probs = fitness/np.sum(fitness) # Probability of individual selection
probs_cum = np.cumsum(probs) # Probability cumulative distribution
each_rand = np.random.uniform(size=len(fitness)) # Get 10 random numbers, between 0 and 1
# Roulette, select a new gene code according to random probability
# For each_ For each random number in Rand, find the chromosome in the roulette
# Code modification
ak = chroms[np.argmax(probs_cum)]
np.delete(chroms,np.argmax(probs_cum))
# Code modification
newX = np.array([chroms[np.where(probs_cum > rand)[0][0]]
for rand in each_rand])
# Reproduction, random pairing (probability 0.6)
# How does the number 6 come from? According to the genetic algorithm, suppose there are 10 numbers, the crossover probability is 0.6, 0 and 1, 2 and 3... 8 and 9, and each group throws a number between 0 and 1
# If this number is less than 0.6, there should be three groups of crossover on average, that is, six chromosomes should be crossed
pairs = np.random.permutation(
int(len(newX)*prob//2 * 2). Reshape (- 1, 2) # generates 6 random numbers. Arrange them randomly and divide them into two columns
center = len(newX[0])//2 # the simplest central crossing method is adopted
for i, j in pairs:
# Cross in the middle
x, y = newX[i], newX[j]
newX[i] = x[:center] + y[center:] # The elements of newX are strings, which can be spliced directly with the + sign
newX[j] = y[:center] + x[center:]
# Code modification
np.append(newX,ak)
# Code modification
return newX