7-1 sum 1 to 100 (10 points)
This problem requires writing a program to calculate the value of expression 1 + 2 + 3 +... + 100.
Input format:
No input for this question.
Output format:
Sum = cumulative sum
Experiment code:
#include<stdio.h>
int main()
{
int sum=0;
for(int i=1;i<=100;i++)
{
sum+=i;
}
printf("sum = %d",sum);
return 0;
}
7-2 sum of the first N items of the square root sequence (15 points)

Input format:
The input gives a positive integer N in one line.
Output format:
In one line, output the value S of the partial sum in the format of "sum = S", accurate to two decimal places. Ensure that the calculation results do not exceed the double precision range.
Input example:
10
Output example:
sum = 22.47
Experiment code:
#include<stdio.h>
#include<math.h>
int main()
{
double sum=0;
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
sum+=sqrt(i);
}
printf("sum = %.2lf",sum);
return 0;
}
7-3 find the sum of the first N items of the nth sequence (15 points)
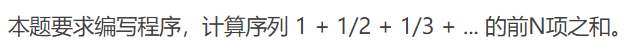
Input format:
The input gives a positive integer N in one line.
Output format:
In one line, output the value S of the partial sum in the format of "sum = S", accurate to 6 decimal places. Ensure that the calculation results do not exceed the double precision range.
Input example:
6
Output example:
sum = 2.450000
Experiment code:
#include<stdio.h>
#include<math.h>
int main()
{
double sum=0;
double n;
scanf("%lf",&n);
for(int i=1;i<=n;i++)
{
sum+=1.0/i;
}
printf("sum = %lf",sum);
return 0;
}
7-4 find the sum of the first N terms of the odd part sequence (15 points)
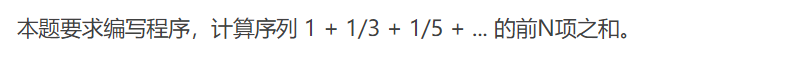
Input format:
The input gives a positive integer N in one line.
Output format:
In one line, output the value S of the partial sum in the format of "sum = S", accurate to 6 decimal places. Ensure that the calculation results do not exceed the double precision range.
Input example:
23
Output example:
sum = 2.549541
Experiment code:
#include<stdio.h>
#include<math.h>
int main()
{
double sum=0;
double n;
scanf("%lf",&n);
for(int i=1;i<=n;i++)
{
sum+=1.0/(2*i-1);
}
printf("sum = %lf",sum);
return 0;
}
7-5 find the sum of the first N items of the simple interleaved sequence (15 points)
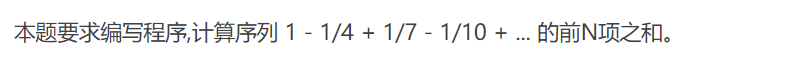
Input format:
The input gives a positive integer N in one line.
Output format:
In one line, output the value S of the partial sum in the format of "sum = S", accurate to three decimal places. Ensure that the calculation results do not exceed the double precision range.
Input example:
10
Output example:
sum = 0.819
Experiment code:
#include <stdio.h>
int main()
{
int n,sign=1,i;
double s=0;
scanf("%d",&n);
for(i=1;i<=n;i++){
s=s+1.0*sign/((i)+2*(i-1));
sign=-sign;
}
printf("sum = %.3lf",s);
return 0;
}
7-6 partial sum of square and reciprocal sequence (15 points)

Input format:
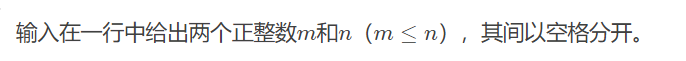
Output format:
In one line, output the value S of the partial sum in the format of "sum = S", accurate to six decimal places. Ensure that the calculation results do not exceed the double precision range.
Input example:
5 10
Output example:
sum = 355.845635
Experiment code:
#include<stdio.h>
#include<math.h>
int main()
{
double m,n,sum=0;
scanf("%lf%lf",&m,&n);
for(m;m<=n;m++)
{
sum+=m*m+1/m;
}
printf("sum = %lf",sum);
return 0;
}
7-7 find the sum of the first N items of the interleaved sequence (15 points)

Input format:
The input gives a positive integer N in one line.
Output format:
Output the value of partial sum in one line, and keep the result to three decimal places.
Input example:
5
Output example:
0.917
Experiment code:
#include<stdio.h>
#include<math.h>
int main()
{
int a,b;
double sum=0,sign=1.0;
scanf("%d",&a);
for(int i=1;i<=a;i++)
{
sum+=sign*i/(2*i-1);
sign=-sign;
}
printf("%.3lf",sum);
return 0;
}
7-8 sum the first N items of the score sequence (15 points)
This problem requires writing a program to calculate the sum of the first N items of sequence 2 / 1 + 3 / 2 + 5 / 3 + 8 / 5 +. Note that the sequence starts from item 2. The molecule of each item is the sum of the previous molecule and the denominator, and the denominator is the molecule of the previous item.
Input format:
The input gives a positive integer N in one line.
Output format:
Output the value of partial sum in one line, accurate to two decimal places. Ensure that the calculation results do not exceed the double precision range.
Input example:
20
Output example:
32.66
Experiment code:
#include<stdio.h>
int main(){
int N;
scanf("%d",&N);
double a=2;
double b=1;
double sum=0;
double exchange=0;
for (double i=1;i<=N;i++){
sum+=a/b;
exchange=a;
a+=b;
b=exchange;
}
printf("%.2f",sum);
return 0;
}
7-9 calculate factorial sum (10 points)
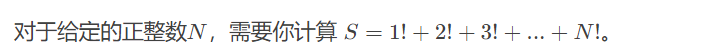
Input format:
The input gives a positive integer N of no more than 10 in one line
Output format:
Output the value of S in one line.
Input example:
3
Output example:
9
Experiment code:
#include<stdio.h>
int main(){
int n;
int sum=0,sum2=1;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
sum2=1;
for(int j=1;j<=i;j++)
{
sum2*=j;
//printf("%d\n",sum2);
}
sum+= sum2;
//printf("%d\n",sum);
}
printf("%d",sum);
return 0;
}
7-10 sum integer segments (10 points)
Given two integers A and B, output all integers from A to B and the sum of these numbers
Input format:
Input gives 2 integers A and B in one line, where − 100 ≤ A ≤ B ≤ 100, separated by spaces.
Output format:
First, all integers from A to B are output sequentially. Every 5 numbers occupy one line, and each number occupies 5 characters wide. Align them to the right. Finally, the sum X of all numbers is output in the format of Sum = X in one line
Input example:
-3 8
Output example:
-3 -2 -1 0 1 2 3 4 5 6 7 8 Sum = 30
Experiment code:
#include <stdio.h>
int main()
{
int x,y,i,a=0,sum=0;
scanf("%d %d",&x,&y);
for(i=x;i<=y;i++)
{
printf("%5d",i);
a++;
sum+=i;
if(a%5==0)
{
printf("\n");
}
}if(a%5!=0) printf("\n");
printf("Sum = %d",sum);
return 0;
}
7-11 output leap year (15 points)
Output all leap years since a certain year in the 21st century. Note: the criterion of leap year is that the year of the year can be divided by 4, but can not be divided by 100, or can be divided by 400.
Input format:
Enter a certain cut-off year for the 21st century in one line
Output format:
Output all leap year years that meet the conditions line by line, that is, each year accounts for one line. If it is not the year of the 21st century, it will output "Invalid year!". If there are no leap years, "None" is output.
Input example:
2048
Output example:
2004 2008 2012 2016 2020 2024 2028 2032 2036 2040 2044 2048
Experiment code:
#include<iostream>
using namespace std;
int main(){
int year,flag=1;
cin>>year;
if(year>=2001 && year<=2100){
for(int i=2001;i<=year;i++){
if((i%4==0 && i%100!=0)||(i%400==0)){
flag=0;
cout<<i<<endl;
}/*else if(flag)
cout<<"None";There are two possibilities here: 1. There is no leap year. 2. If the first time is not a leap year, none will be output
However, leap years may be output later, which is inconsistent with the title*/
}
if(flag)
cout<<"None";
}else
cout<<"Invalid year!";
return 0;
}
7-12 find out the number of three daffodils (15 points)
This problem requires writing a program to output all three digit daffodils in the interval of a given positive integer M and N. The three digit daffodil number, that is, the cubic sum of its single digit, ten digit and hundred digit number is equal to the number itself.
Input format:
Input gives two positive integers M and N in one line (100 ≤ M ≤ n ≤ 999).
Output format:
`Sequentially output all three digit daffodils in the M and N intervals, and one number in each line. If there are no three digit daffodils in this interval, there is no output.
If M or N does not meet the requirements of the topic, Invalid Value is output** Input sample: * * 100 400 * * output sample: * * 153
370
371`
Experiment code:
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<math.h>
int main() {
int m, n;
scanf("%d%d", &m, &n);
if (m <= n && m >= 100 && n <= 999) {
int i;
for (i = m; i <= n; i++) {
int x, y, z;
x = i / 100;
y = i % 100 / 10;
z = i % 10;
if (pow(x, 3) + pow(y, 3) + pow(z, 3) == i) {
printf("%d\n", i);
}
}
}
else {
printf("Invalid Value.");
}
return 0;
}
7-13 find the minimum value (20 points)
This problem requires writing a program to find the minimum value in a given series of integers
Input format:
The input first gives a positive integer n in a line, followed by N integers separated by spaces.
Output format:
Output the minimum value of n integers in the format of "min = minimum value" in one line.
Input example:
4 -2 -123 100 0
Output example:
min = -123
Experiment code:
#include <stdio.h>
int main(void){
int n, i, k, min=1000000;
scanf("%d", &n);
for(i = 0; i < n; i++){
scanf("%d", &k);
if( k < min ) min = k;
}
printf("min = %d", min);
return 0;
}
7-14 hundred money hundred chicken (10 points)
Chicken question: "today, there is a chicken Weng one, which is worth five; a chicken mother one, which is worth three; and a chicken chick three, which is worth one. If you buy a hundred chickens for a hundred dollars, ask the chicken Weng, the mother and the chicks how much they are."
The hundred chicken problem is a world-famous indefinite equation problem proposed by the mathematician Zhang Qiujian of the Northern Wei Dynasty in Zhang Qiujian's calculation classic. It gives the solution of an indefinite equation system composed of two equations with three unknowns.
Since Zhang Qiujian, Chinese mathematicians have been deepening the research on the hundred chicken problem, and the hundred chicken problem has almost become synonymous with the indefinite equation. The mathematical research on the hundred chicken problem has made good achievements from the Song Dynasty to the Qing Dynasty.
Zhang Qiu Jian Suan Jing was written in about 466-485 ad, with 93 questions in three volumes, including calculation problems in measurement, textile, exchange, tax payment, smelting, civil engineering, interest and so on. Its style is question and answer, well-organized and elegant. It is not only a masterpiece in the history of ancient Chinese mathematics, but also a valuable heritage in the world mathematics database. Later scholars Zhen Luan of the Northern Zhou Dynasty and Li Chunfeng of the Tang Dynasty annotated the book one after another. Especially in the Tang Dynasty, Li Chunfeng was ordered by the Taishi to annotate and sort out, which was included in the ten books of Suanjing, which became a must read bibliography for students of the suanjuan at that time. There are 92 questions in the current edition of Zhang Qiu Jian Suanjing. The outstanding achievements include the calculation of the maximum common divisor and the minimum common multiple, the solution of various arithmetic sequence problems, the solution of some indefinite equation problems, etc.
(the above text is extracted from Baidu Encyclopedia)
The vernacular version of the problem of 100 money and 100 chickens: 100 yuan for 100 chickens, 5 yuan for a rooster, 3 yuan for a hen and 1 yuan for 3 chicks. How many cocks, hens and chicks are there (0 for a certain chicken)?
The result of 100 money and 100 chicken is shown in the output example.
Now change 100 to N, that is, n yuan to buy n chickens. The prices of all kinds of chickens remain unchanged. What is the result?
Input format:
There are multiple groups of test data, which are processed to the end of the file. Enter an integer n (100 < = n < = 1000) for each set of tests
Output format:
For each group of tests, various buying methods are output line by line according to the number of roosters, hens and chicks (in the order of the number of roosters from small to large) (there is a space between each line of data).
Input example:
100
Output example:
0 25 75 4 18 78 8 11 81 12 4 84
Experiment code:
/*100 100 chickens, 5 cocks, 3 hens and 1 chicken for three chicks*/
#include<stdio.h>
int main() {
int n;
int count=1;
scanf("%d",&n);
int gj, mj, xj,i,j;
for (i = 0; i < n;i++) {
for (j = 0; j < n;j++) {
if (i / 3 + j * 5 + (n - i - j) * 3 == n && i % 3 == 0 && i >= 0 && j >= 0 && (n-i-j)>=0) {
printf("%d %d %d\n",j,(n-i-j),i);
count++;
break;
}
}
}
return 0;
}