dijkstra has four steps:

1. Set the starting distance to 0
2. Cycle n times
3. Find the point with the shortest distance outside the set each time and put it into the set
4. Update the distance of all points connected to it with the points just put in

The idea is to update the minimum value of other points by using the point with the shortest distance outside the set every time according to greed. There are n points in total, so a total of N cycles (in fact, it is OK to cycle n-1 times, because the last point of the last cycle must have been better by all the remaining points). In this way, the distance of the end point after the update must be the shortest distance

for instance:

For the following figure

At the beginning, set dist[1]=0, and update the distance of the points connected with it with v1. Note: the distance of v5, v6 and other points that have not been marked with distance should be initialized to 0x3f3f3f3f, which is the following. It was forgotten to add it when drawing

 

 

  The blue circle indicates which point is currently updated, and the red circle indicates the updated point

 

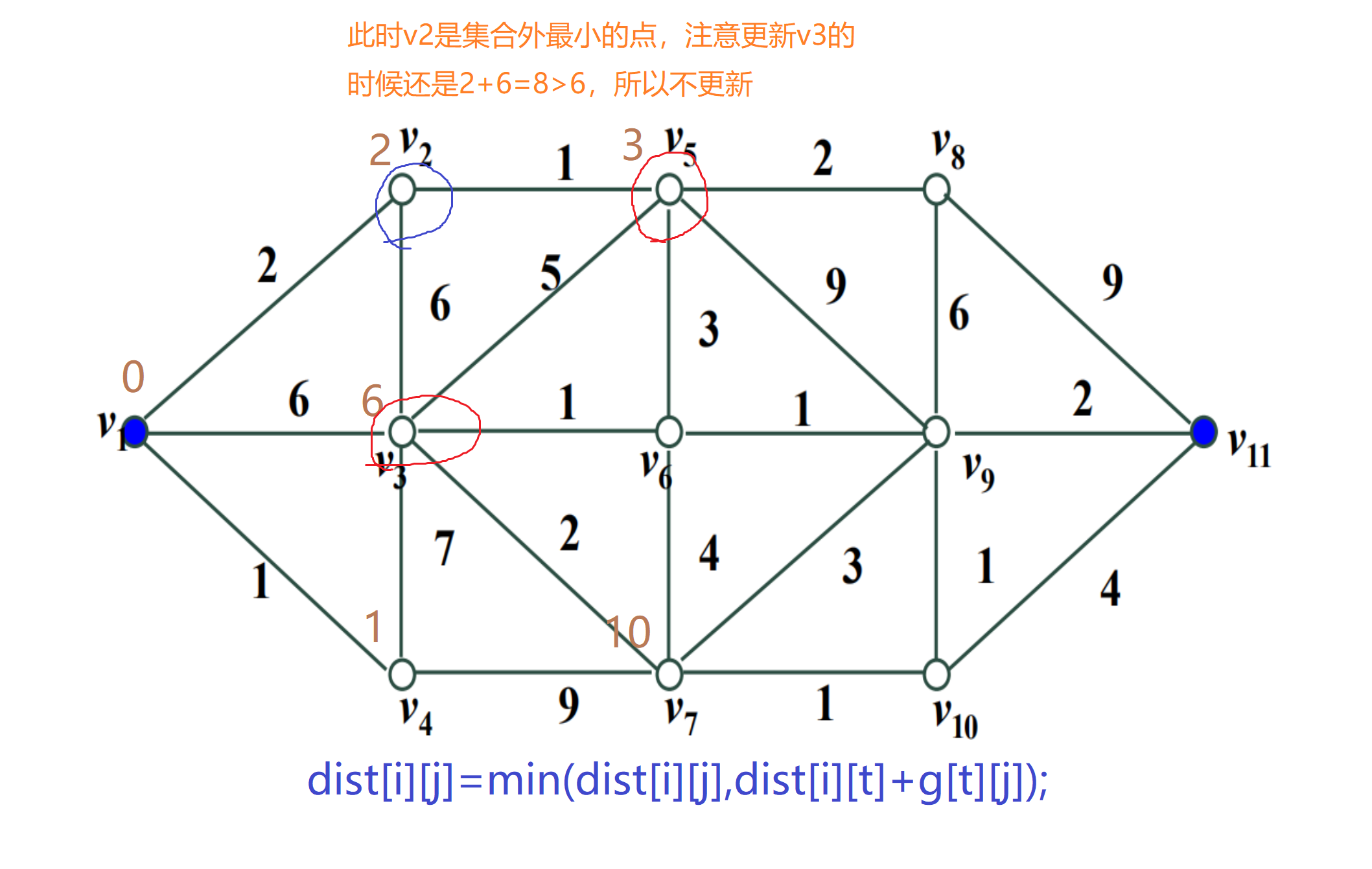
Add the following green triangle to indicate the points already in the set

Pay attention to the following picture. Your hand is wrong! The blue character should be 11 < 12. Sorry, it can't be changed

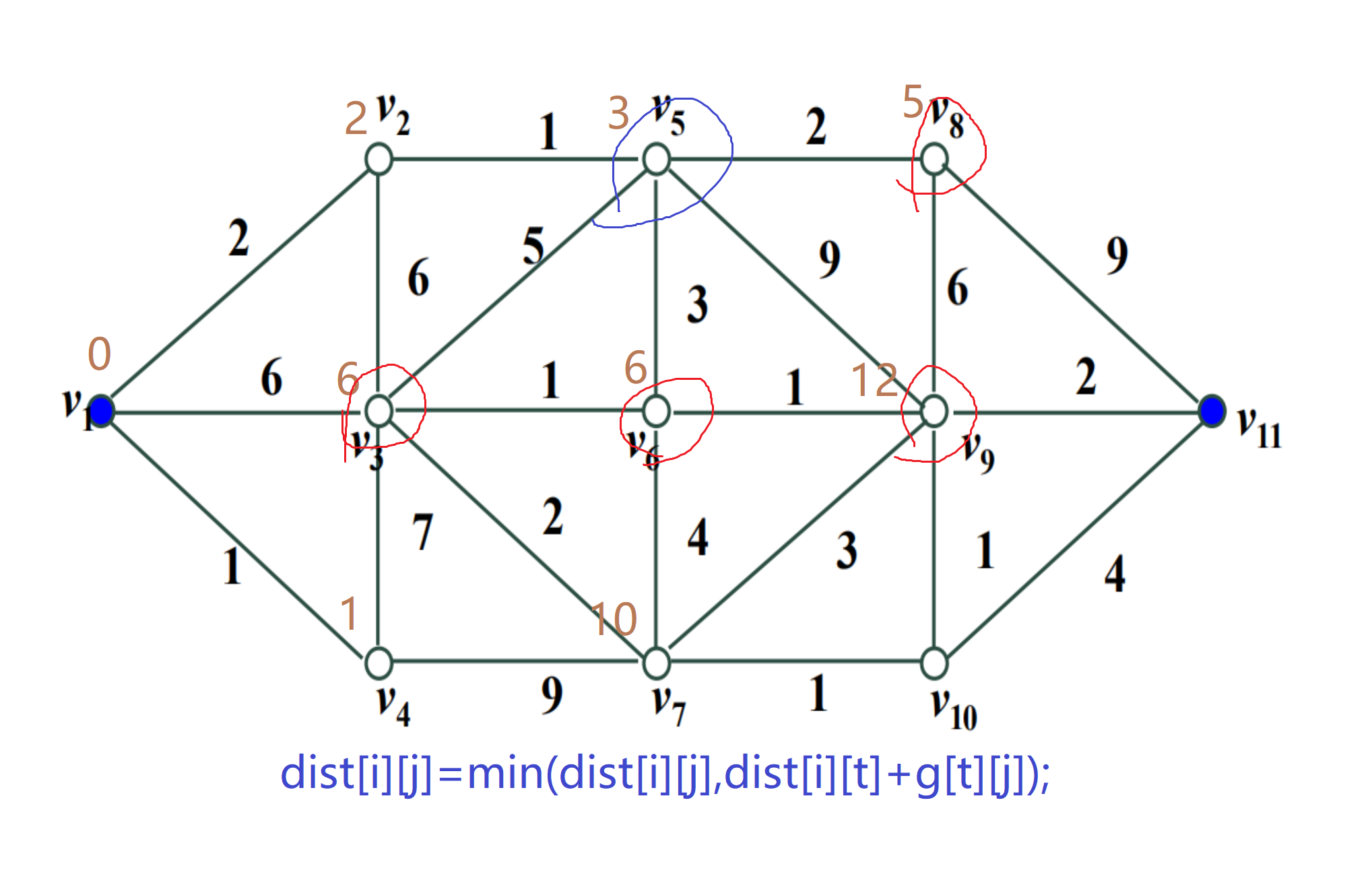
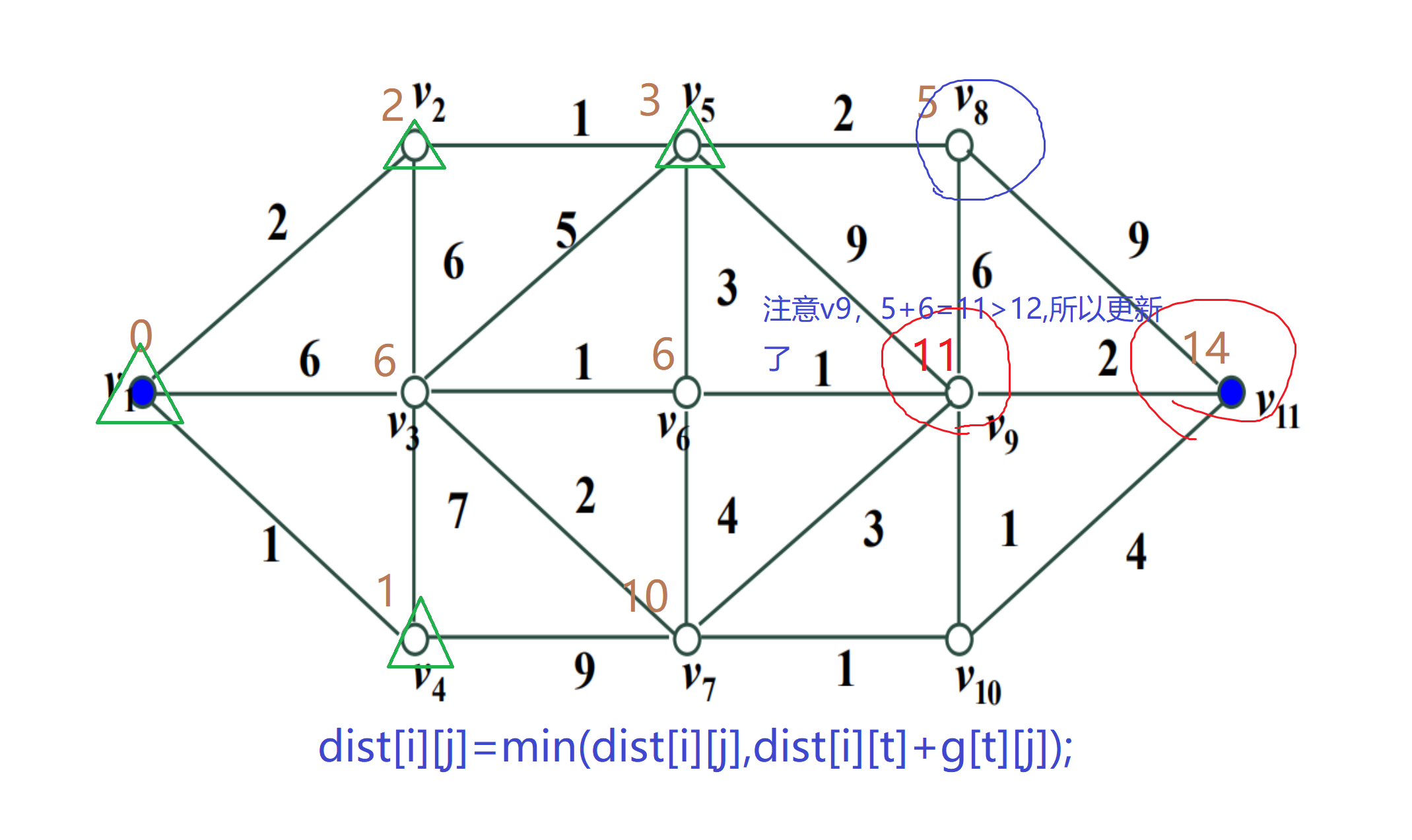The next step is to repeat the above process update. All possible situations have been mentioned in the above diagrams. Because this diagram is complex, the processes are not listed one by one, and the results are given directly here

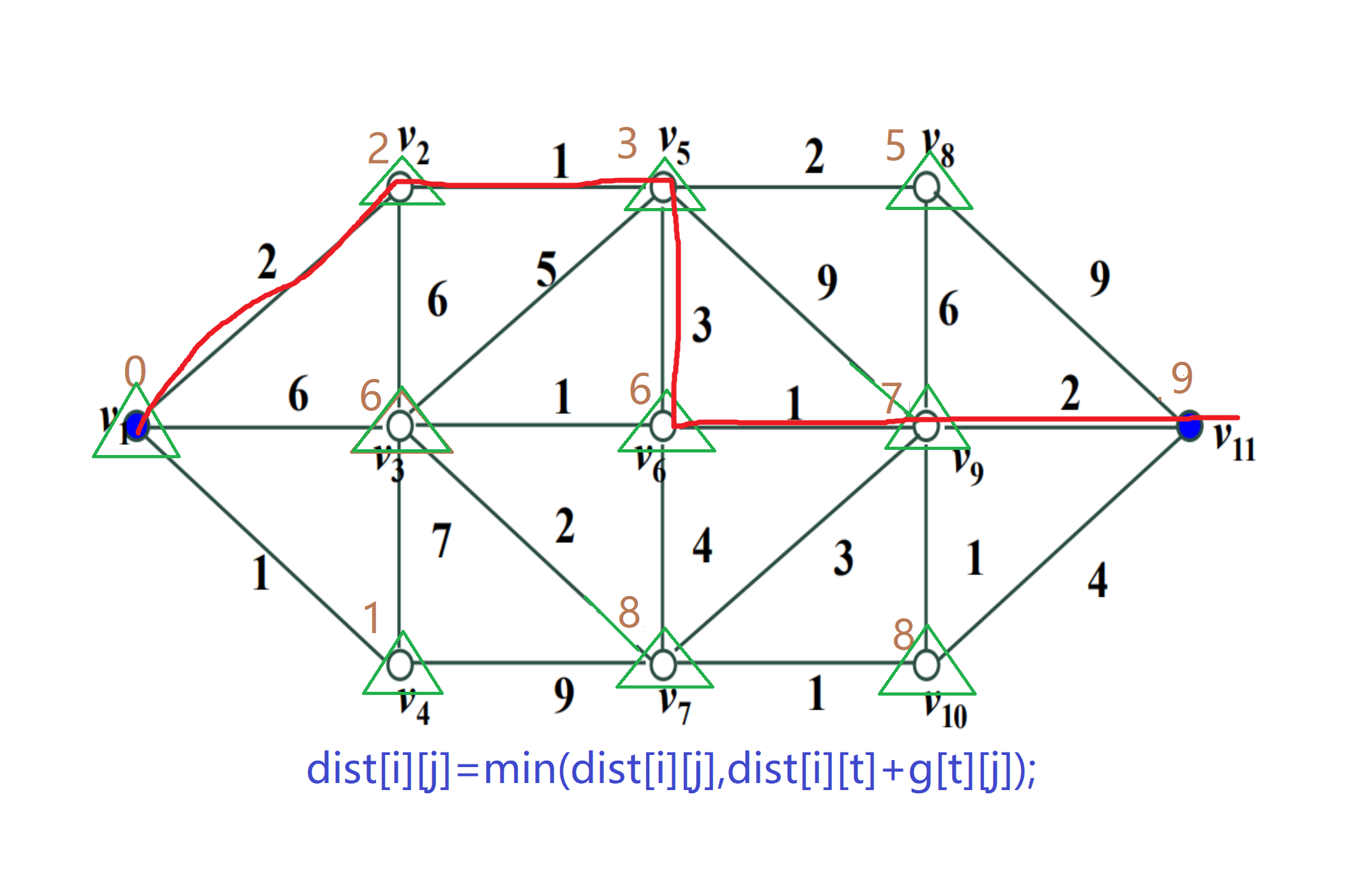
So far, the shortest path update is completed, and the shortest distance is 9

The template code is given below. See the notes for details

Code:

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1e4+10;
int dist[N];
int g[501][501];//This template uses adjacency matrix, which is not suitable for sparse graphs, and the space may explode
int n,m;
bool st[501];
int dijk()
{
    memset(dist, 0x3f,sizeof dist);//The initial initialization of all edges, 0x3f3f3f3f, is the decimal int limit, which can be considered as positive infinity
    dist[1]=0;
   for(int i=0;i<n;i++)
    {
        int t=-1;
        for(int j=1;j<=n;j++)//Traverse all points to find the smallest point outside the set
        {
             if(!st[j]&&(t==-1||dist[t]>dist[j]))//If (outside the set & & (no point has been selected | smaller points can be selected))
             t=j;
        }
        st[t]=true;//Join collection
       for(int j=1;j<=n;j++)//Update the distance of all points with the distance of the points just added to the set
       {
           dist[j]=min(dist[j],dist[t]+g[t][j]);//Min (distance from 1 to j, distance from 1 to t + distance from t to j)
       }


    }
   if(dist[n]==0x3f3f3f3f) return -1;//If not connected
    return dist[n];
}
int main()
{
    cin>>n>>m;
    memset(g,0x3f,sizeof g);
    while(m--)
    {
        int x,y,z;
        cin>>x>>y>>z;
        g[x][y]=min(g[x][y],z);//When dealing with multiple edges, it is natural to retain the least edge weight
    }
    printf("%d",dijk());
    return 0;
}

Next, let's talk about the heap optimized version of dijkstra

Heap optimization is actually a modification and Optimization Based on the simple version of dijkstra. Deformation refers to changing the adjacency matrix into an adjacency table. Optimization refers to optimizing the time complexity of "traversing all points and finding the smallest point outside the set" into O(logn) by using the priority queue. In addition, the heap optimization version of dijkstra can deal with dense and sparse graphs, The plain version can only deal with dense graphs.

Its principle and idea are exactly the same as that of the plain version. It will not be repeated here. The template code is given directly:

Code:

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 2e5+10;
typedef pair<int, int> PII;
int h[N], e[N], ne[N], idx, w[N];
int dist[N];
int n,m;
bool st[N];
void add(int a, int b, int c)//Adjacency table, add an edge with a - > b, and the weight is c
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int dijkstra()
{
    memset(dist,0x3f,sizeof dist);
    dist[1]=0;
    priority_queue<PII,vector<PII>,greater<PII>> q;//Use the priority queue to eliminate the cycle of finding points
    q.push({0,1});
    while(q.size())
    {
        auto t=q.top();//Just update with the team head every time
        q.pop();
        if(st[t.second]) continue;
        st[t.second]=true;
        for(int i=h[t.second];i!=-1;i=ne[i])//Traverse all edges connected to this point
        {
            int j=e[i];
            if(dist[j]>dist[t.second]+w[i])
            {
                dist[j]=dist[t.second]+w[i];
                q.push({dist[j],j});
            }
        }
    }
    if(dist[n]==0x3f3f3f3f) return -1;
    return dist[n];
}
int main()
{
    memset(h, -1, sizeof h);
    cin>>n>>m;
    while (m -- )
    {
        int a,b,c;
        cin>>a>>b>>c;
        add(a, b, c);
    }
    cout<<dijkstra()<<endl;
    return 0;
}

Author: mechanical tolerance
Link: https://www.acwing.com/activity/content/code/content/1498175/
Source: AcWing
The copyright belongs to the author. For commercial reprint, please contact the author for authorization, and for non-commercial reprint, please indicate the source.