subject

There is a large rectangular cake, the length and width are integers w and h respectively. Now to cut it into m small cakes, each small cake must be rectangular and have an integer length and width. When cutting a cake, cut one cake at a time and divide it into two rectangular cakes. Please calculate the lower limit of the area of the largest of the M small cakes.

Assuming w = 4, H = 4 and M = 4, the following cutting method can minimize the area of the largest cake.

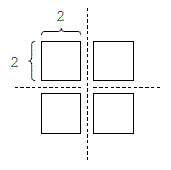
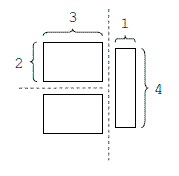
Assuming w = 4, H = 4 and M = 3, the following cutting method will minimize the area of the largest cake:

input

There are multiple lines, and each line represents a test case. Each line is three integers w, h, m separated by spaces, where 1 ≤ w, h, m ≤ 20, m ≤ wh When w = h = m = 0, no processing is required, indicating the end of input.

output

The results of each test case occupy one line, and an integer is output to represent the lower limit of the area of the largest cake block.

sample input

4 4 4
4 4 3
0 0 0

sample output

4
6

Problem solving ideas

1. Finding the optimal substructure
   Cut a cake of size w * h into m pieces, and cut it m-1 times to find the minimum value of the largest cake in the m pieces of cake. According to the definition of dynamic programming algorithm, the problem is decomposed into several subproblems to obtain the final solution. That is, cut it once to get the minimum value of the largest block in the two cakes and store it. Based on the solution of this subproblem, the minimum value obtained by cutting twice is calculated and stored to calculate the solution of the next subproblem. And so on until the final solution is obtained.

2. Inductive state transition equation
   Establish a three-dimensional array ways(w, h, m), w=1, 2... W, h=1, 2... H, m=0, 1, 2... M-1, which represents the minimum value of the maximum cake obtained by cutting the cake with the size of w * h for m times.
   

SV represents the optimal solution of the first knife vertical cutting:
SV = min{Si}, i = 1, 2... W-1, Si = the optimal solution of the first knife cut vertically at the ith position
Si = max {ways (I, h, K), ways (w-i, h, m-k-1)}, k = 0, 1... M-1 compare the optimal solution of cutting I knife on the left and m-1-i knife on the right, and take the larger one
SH represents the optimal solution of the first knife cross cutting:
SH = min{Si}, i = 1, 2... W-1, Si = the optimal solution of the first knife at the ith position
Si = max {ways (W, I, K), ways (W, H-I, m-k-1)}, k = 0, 1... M-1 compare the optimal solution of cutting I knife on the upper edge and cutting m-1-i knife on the lower edge, and take the larger one

Code implementation:

Recursive method:

# include <iostream>
# include <string.h>

using namespace std;

const int INF = 0xfffffff; //Used to represent infinity 
int ways[22][22][22]; //Used to store the current status 

int Divid_the_cake(int w, int h, int m)
{
	if(w * h < m + 1){
		ways[w][h][m] = INF;
		return INF;
	} 
	else if(!m)
	{
		ways[w][h][m] = w * h;
		return w * h;
	 } 
	else if(ways[w][h][m]) return ways[w][h][m];
	
	int maxV = INF;
	int maxH = INF;
	for(int i = 1; i < w; i++){ //The first knife is cut vertically in the i position
		for(int j = 0; j < m; j++){ // Compare the optimal solution of the left cutting I knife and the right cutting m-1-i knife, and take the larger one 
			maxV = min(maxV, max(Divid_the_cake(i, h, j), Divid_the_cake(w - i, h, m - j - 1)));
		}
	}
	for(int i = 1; i < h; i++){ //The first knife cuts horizontally in i position 
		for(int j = 0; j < m; j++){ //Compare the optimal solution of upper cutting I knife and lower cutting m-1-i knife, and take the larger one 
			maxH = min(maxH, max(Divid_the_cake(w, i, j), Divid_the_cake(w, h - i, m - j - 1)));
		}
	}

	ways[w][h][m] = min(maxV,maxH); // Select the optimal solution of vertical tangent and horizontal tangent 
	
	return ways[w][h][m];
}

int main()
{
	int w,h,m;

	memset(ways,0,sizeof(ways));
    Divid_the_cake(22,22,22);
	while(cin >> w >> h >> m && w && h && m) {
		cout << ways[w][h][m - 1] <<endl;
	}

    return 0;
}

Recursive method

# include <iostream>
# include <string.h>

using namespace std;

const int INF = 0x3f3f3f3f; //Used to represent infinity 
int ways[22][22][22]; //Store the data of the optimal solution, that is, the minimum area of the largest cake when cut into m pieces of cake 

int main()
{
	int w,h,m;
	
	memset(ways,INF,sizeof(ways));
	for(int i = 1; i <= 22; ++i){
		for(int j = 1; j <= 22; ++j){ //Cake size from small to large 
			for(int k = 0; k <= 22; ++k){//The number of cake cutters increases from small to large
                if(ways[j][i][k] != INF) ways[i][j][k] = ways[j][i][k]; //The symmetry of the cake is used for optimization
				else if(i * j < k + 1) ways[i][j][k] = INF;
				else if(!k) ways[i][j][k] = i * j;
				else{
					for(int ii = 1; ii < i; ++ii) //The first knife is cut vertically in the second position
						for(int kk = 0; kk < k; ++kk) //Compare the optimal solution of the left KK cutter and the right k-1-kk cutter, and take the larger one
							ways[i][j][k] = min(ways[i][j][k], max(ways[ii][j][kk], ways[i - ii][j][k - kk - 1]));
					for(int jj = 1; jj < j; ++jj) //The first knife cuts horizontally in the second position
						for(int kk = 0; kk < k; ++kk) //Compare the optimal solution of the upper cutting KK cutter and the lower cutting k-1-kk cutter, and take the larger one 
							ways[i][j][k] = min(ways[i][j][k], max(ways[i][jj][kk], ways[i][j - jj][k - kk - 1]));
				}
			}
		}
	}
	
	while(cin >> w >> h >> m && w && h && m) cout << ways[w][h][m - 1] <<endl;
	
	return 0;
 }

Optimization of recursive method:

The recursive method is optimized by symmetry. The solution obtained by cutting the cake with width w and height h m times is actually the same as that obtained by cutting the cake with width h and height w M times. Therefore, when the ways(w,h,m) is calculated, we can know the ways(h,w,m). That is, conditions are added to the code of recursive method

if(ways[j][i][k] != INF) ways[i][j][k] = ways[j][i][k];