1, Directed graph

In real life, many application related graphs are directional. The most intuitive is the network. You can jump from page a to page B through links. Then the direction of a and B connection is a - > b, but it can not be said to be B - > A. at this time, we need to use a directed graph to solve this kind of problem. The biggest difference between it and the undirected graph we learned before is that the connection has direction, There will also be great differences in the processing of code.

1.1 definition of directed graph and related terms

definition:
A directed graph is a directional graph, which is composed of a group of vertices and a group of directional edges. The edges in each direction are connected with a pair of ordered vertices.
Output:
The number of edges indicated by a vertex is called the extroversion of the vertex.
Penetration:
The number of edges pointing to a vertex is called the penetration of the vertex.
Directed path:
It consists of a series of vertices. For each vertex, there is a directed edge from which to point to the next vertex in the sequence.
Directed ring:
A directed path that contains at least one edge and has the same start and end points.

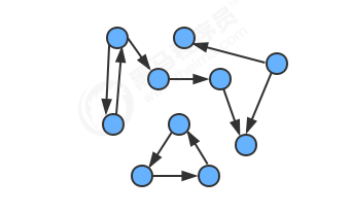
The two vertices v and w in a directed graph may have the following four relationships:

1. No edges connected;
2. There is an edge from v to w, v - > w;
3. There is an edge w > v from w to v;
4. There are both sides from w to v and sides from v to W, that is, two-way connection;

It is easy to understand a directed graph, but it is not so easy to see the path in a complex directed graph through the eyes.

1.2 directed graph API design

Class name	Digraph
Construction method	Digraph(int V): creates a directed graph with V vertices but no edges
Member method	1.public int V(): get the number of vertices in the graph 2.public int E(): get the number of edges in the graph 3.public void addEdge(int v,int w): add an edge V - > w to the directed graph 4.public Queue adj(int v): get all vertices connected by the edge indicated by v 5.private Digraph reverse(): the reverse of the graph
Member variable	1.private final int V: record the number of vertices 2.private int E: number of recording edges 3.private Queue[] adj: adjacency table

A reverse graph is designed in the api, because in the implementation of directed graph, the other vertices pointed by the current vertex v are obtained by adj method. If we can get its reverse graph, we can easily get other vertices pointing to v.

1.3 implementation of directed graph

public class Digraph {
    //Number of vertices
    private final int V;
    //Number of edges
    private int E;
    //Adjacency table
    private Queue<Integer>[] adj;

    public Digraph(int V){
        //Number of initialization vertices
        this.V = V;
        //Number of initialization edges
        this.E = 0;
        //Initialize adjacency table
        this.adj = new Queue[V];
        for (int i = 0; i < adj.length; i++) {
            adj[i] = new Queue<Integer>();
        }
    }

    //Gets the number of vertices
    public int V(){
        return V;
    }

    //Gets the number of edges
    public int E(){
        return E;
    }

    //Add an edge to the directed graph V - > W
    public void addEdge(int v, int w) {
        //You only need to make vertex w appear in the adjacency table of vertex v, because the edges have directions. Finally, the meaning of adjacent vertices stored in the adjacency table of vertex v is: V - > other vertices
        adj[v].enqueue(w);
        E++;
    }

    //Gets all vertices connected by the edge indicated by v
    public Queue<Integer> adj(int v){
        return adj[v];
    }

    //Reverse graph of the graph
    private Digraph reverse(){
        //Create a directed graph object
        Digraph r = new Digraph(V);

        for (int v = 0;v<V;v++){
            //Gets all edges indicated by the vertex v
            for (Integer w : adj[v]) {//The edge represented in the original figure is composed of vertex v - > W
                r.addEdge(w,v);//w->v
            }
        }
        return r;
    }
}

2, Topological sorting

In real life, we often receive many tasks at one time, but these tasks are completed in order. Taking the subject of java as an example, we need to learn a lot of knowledge, but these knowledge needs to be completed in order in the process of learning. It is a step-by-step and dependent process from java foundation to jsp/servlet, to ssm, to spring boot, etc. Before learning jsp, you should first master the basics of java and html, and jsp/servlet before learning ssm framework.

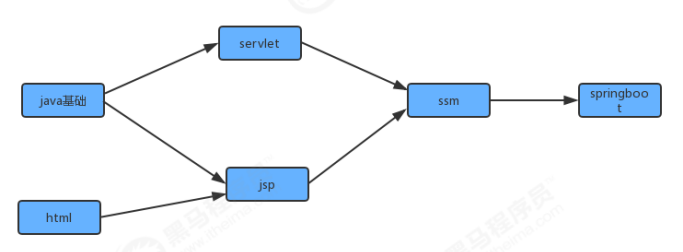
In order to simplify the problem, we use the standard model with integer vertex number to represent this case:

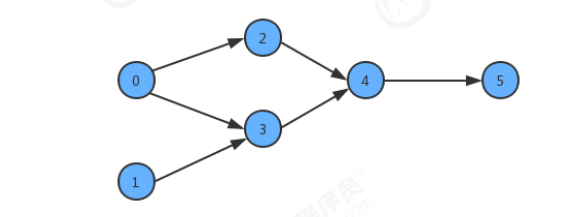
At this time, if a student wants to learn these courses, he needs to specify a learning scheme. We only need to sort the vertices in the graph and convert them into a linear sequence to solve the problem. At this time, we need to use an algorithm called topological sorting.

Topology sorting:
Given a directed graph, all vertices are sorted so that all directed edges point from the front element to the back element. At this time, the priority of each vertex can be clearly expressed. The following is a schematic diagram after topology sorting:

2.1 detecting rings in directed graphs

If you have to learn course y before learning course x, course z before learning course y, and course x before learning course z, there must be a problem. We can't learn because these three conditions can't be met at the same time. In fact, the conditions of these three courses x, y and z form a ring:

Therefore, if we want to use topological sorting to solve the priority problem, we must first ensure that there are no rings in the graph.

2.1. 1 API design for detecting directional ring

Class name	DirectedCycle
Construction method	DirectedCycle(Digraph G): create a detection ring object to detect whether there is a ring in Figure G
Member method	1.private void dfs(Digraph G,int v): detect whether there is a ring in Figure G based on depth first search 2.public boolean hasCycle(): judge whether there is a ring in the diagram
Member variable	1.private boolean[] marked: the index represents the vertex, and the value indicates whether the current vertex has been searched 2.private boolean hasCycle: record whether there is a ring in the diagram 3.private boolean[] onStack: the index represents the vertex. The idea of stack is used to record whether the current vertex is already on the directed path being searched

2.1. 2. Implementation of detection directed ring

onStack [] Boolean array is added to the API, and the index is the vertex of the graph. When we search deeply:

1. If the current vertex is being searched, change the value in the corresponding onStack array to true and mark it into the stack;
2. If the current vertex search is completed, change the value in the corresponding onStack array to false to identify the stack;
3. If you are about to search for a vertex, but the vertex is already on the stack, there is a ring in the graph;

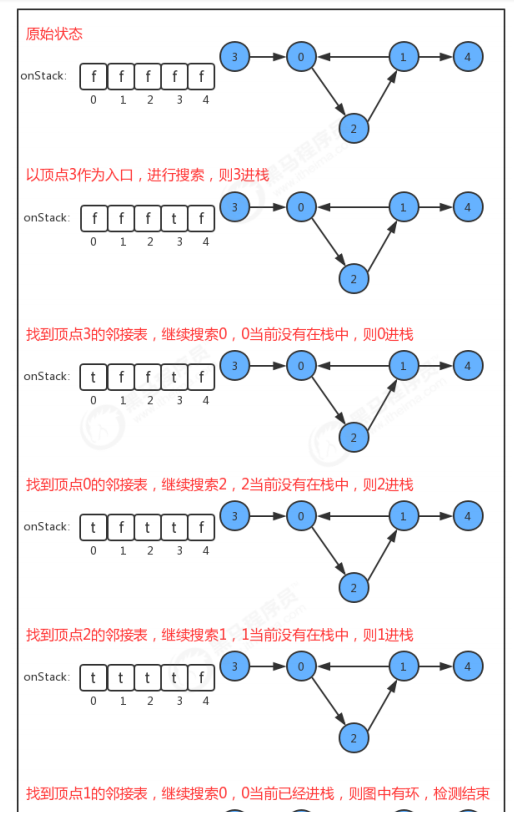
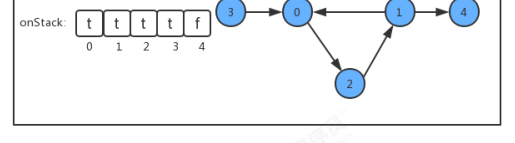
code:

public class DirectedCycle {
    //The index represents the vertex, and the value indicates whether the current vertex has been searched
    private boolean[] marked;
    //Record whether there are rings in the drawing
    private boolean hasCycle;
    //The index represents the vertex. The idea of stack is used to record whether the current vertex is already on the directed path being searched
    private boolean[] onStack;

    //Create a detection ring object to detect whether there is a ring in Figure G
    public DirectedCycle(Digraph G){
        //Initialize marked array
        this.marked = new boolean[G.V()];
        //Initialize hasCycle
        this.hasCycle = false;
        //Initialize onStack array
        this.onStack = new boolean[G.V()];

        //Find each vertex in the graph, let each vertex as the entry, and call dfs for search once; Avoiding directed rings in unconnected graphs
        //Vertices marked as true no longer need to be searched as entries
        for (int v =0; v<G.V();v++){
            //Judge if the current vertex has not been searched, call dfs to search
            if (!marked[v]){
                dfs(G,v);
            }
        }
    }

    //Based on the depth first search, whether there is a ring in Fig. G is detected
    private void dfs(Digraph G, int v){
        //The vertex v is represented as searched
        marked[v] = true;

        //Stack the current vertex
        onStack[v] = true;

        //Perform a deep search
        for (Integer w : G.adj(v)) {
            //Judge that if the current vertex w has not been searched, continue to recursively call the dfs method to complete the depth first search
            if (!marked[w]){
                dfs(G,w);
            }

            //Judge whether the current vertex w is already in the stack. If it is already in the stack, it proves that the current vertex was in the searching state before, and now it will search again to prove that the ring is detected
            if (onStack[w]){
                hasCycle = true;
                return;
            }
        }
        //Stack the current vertex
        onStack[v] = false;
    }

    //Judge whether there is a ring in the current directed graph G
    public boolean hasCycle(){
        return hasCycle;
    }
}

2.2 vertex sorting based on depth first

If we want to generate a linear sequence of vertices in a graph, it is actually a very simple thing. We have learned and used depth first search many times before. We will find that depth first search has a feature, that is, on a connected subgraph, each vertex will only be searched once. If we can add a line of code on the basis of depth first search, We can do this by simply putting the search vertices into the data structure of the linear sequence.

2.2. 1 Vertex sorting API design

Class name	DepthFirstOrder
Construction method	DepthFirstOrder(Digraph G): create a vertex sorting object to generate a linear sequence of vertices;
Member method	1.private void dfs(Digraph G,int v): generates a linear sequence of vertices based on depth first search 2.public Stack reversePost(): gets the linear sequence of vertices
Member variable	1.private boolean[] marked: the index represents the vertex, and the value indicates whether the current vertex has been searched 2.private Stack reversePost: use stack to store vertex sequences

2.2. 2. Implementation of vertex sorting

In the design of API, we add a stack reversePost to store vertices. When we search the graph in depth, we put the vertex into reversePost after each vertex is searched, so that vertex sorting can be realized.

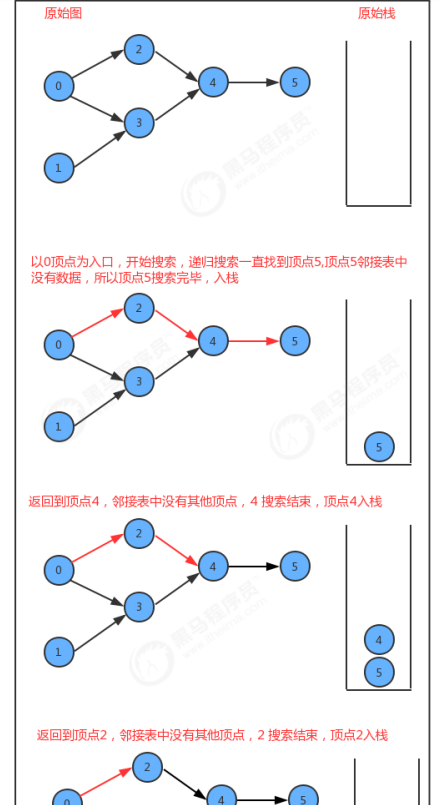
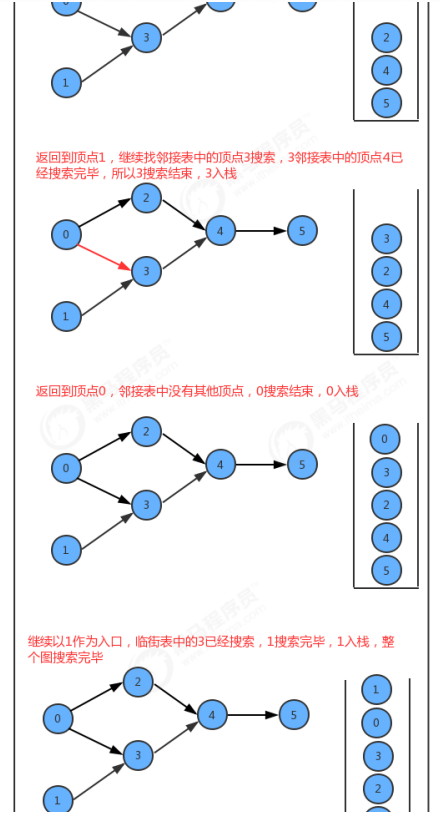
code:

public class DepthFirstPaths {
    //The index represents the vertex, and the value indicates whether the current vertex has been searched
    private boolean[] marked;
    //starting point
    private int s;
    //The index represents the vertex, and the value represents the last vertex on the path from the starting point s to the current vertex
    private int[] edgeTo;

    //Construct the depth first search object, and use the depth first search to find all paths with the starting point of s in the G graph
    public DepthFirstPaths(Graph G, int s){
        //Initialize marked array
        this.marked = new boolean[G.V()];
        //Initialization starting point
        this.s = s;
        //Initialize edgeTo array
        this.edgeTo = new int[G.V()];

        dfs(G,s);
    }

    //Use depth first search to find all adjacent vertices of v vertex in G graph
    private void dfs(Graph G, int v){
        //Represent v as searched
        marked[v] = true;

        //Traverse the adjacency table of vertex v, get each adjacent vertex, and continue the recursive search
        for (Integer w : G.adj(v)) {
            //If the vertex w is not searched, the recursive search continues

            if (!marked[w]){
                edgeTo[w] = v;//The last vertex on the path to vertex w is v
                dfs(G,w);
            }
        }
    }

    //Judge whether there is a path between w vertex and s vertex
    public boolean hasPathTo(int v){
        return marked[v];
    }

    //Find the path from the starting point s to the vertex v (that is, the vertex through which the path passes)
    public Stack<Integer> pathTo(int v){
        if (!hasPathTo(v)){
            return null;
        }

        //Create a stack object and save all vertices in the path
        Stack<Integer> path = new Stack<>();

        //Through the loop, start from vertex v and look forward until you find the starting point
        for (int x = v; x!=s;x = edgeTo[x]){
            path.push(x);
        }

        //Put the starting point s on the stack
        path.push(s);

        return path;
    }
}

2.3 topology sorting implementation

Ring detection and vertex sorting have been implemented earlier, so topological sorting is very simple. Based on a graph, first detect whether there is a ring. If there is no ring, call vertex sorting.
API design:

Class name	TopoLogical
Construction method	TopoLogical(Digraph G): construct topology sorting objects
Member method	1.public boolean isCycle(): judge whether there is a ring in Figure G 2.public Stack order(): get all vertices of topology sorting
Member variable	1.private Stack order: topological sorting of vertices

code:

public class TopoLogical {
    //Topological sorting of vertices
    private Stack<Integer> order;

    //Construct topology sort objects
    public TopoLogical(Digraph G) {
        //Create an object that detects a directed ring
        DirectedCycle cycle = new DirectedCycle(G);
        //Judge whether there is a ring in the G graph. If there is no ring, perform vertex sorting: create a vertex sorting object
        if (!cycle.hasCycle()){
            DepthFirstOrder depthFirstOrder = new DepthFirstOrder(G);
            order = depthFirstOrder.reversePost();
        }
    }

    //Judge whether there is a ring in Figure G
    private boolean isCycle(){
        return order==null;
    }

    //Gets all vertices sorted by topology
    public Stack<Integer>  order(){
        return order;
    }
}

3, Weighted undirected graph

Weighted undirected graph is a graph model that associates a weight value or cost for each edge. This graph can naturally represent many applications. In an aeronautical chart, the edge represents the route, and the weight can represent the distance or cost. In a circuit diagram, the edge represents the wire, and the weight may represent the length of the wire, that is, the cost, or the time required for the signal to pass through the wire. At this time, we can easily think of the problem of minimum cost. For example, how to fly from Xi'an to New York to minimize the time cost or money cost?

In the figure below, there are three paths from vertex 0 to vertex 4, namely 0-2-3-4, 0-2-4, 0-5-3-4. What is the best path for us to reach vertex 4? At this point, we should consider which path has the lowest cost.

3.1 representation of edges of weighted undirected graphs

We can not simply use v-w two vertices to represent the edges in a weighted undirected graph, but must associate a weight value to the edges, so we can use objects to describe an edge.
API design:

Class name	Edge implements Comparable
Construction method	Edge(int v,int w,double weight): construct an edge object from vertices v and W and weight values
Member method	1.public double weight(): get the weight value of the edge 2.public int either(): get a point on the edge 3. Public int other (int vertex): get another vertex on the edge except vertex vertex 4.public int compareTo(Edge that): compares the weights of the current edge and the parameter that edge. If the weight of the current edge is large, it returns 1; if it is the same, it returns 0; if the weight is small, it returns - 1
Member variable	1.private final int v: vertex i 2.private final int w: vertex 2 3.private final double weight: the weight of the current edge

code:

public class Edge implements Comparable<Edge> {
    private final int v;//Vertex one
    private final int w;//Vertex two
    private final double weight;//The weight of the current edge

    //Construct an edge object from vertices v and w and weight values
    public Edge(int v, int w, double weight) {
        this.v = v;
        this.w = w;
        this.weight = weight;
    }

    //Gets the weight value of the edge
    public double weight(){
        return weight;
    }

    //Gets a point on the edge
    public int either(){
        return v;
    }

    //Gets another vertex on the edge except vertex vertex
    public int other(int vertex){
        if (vertex==v){
            return w;
        }else{
            return v;
        }
    }

    @Override
    public int compareTo(Edge that) {
        //Use a traversal record to compare the results
        int cmp;

        if (this.weight()>that.weight()){
            //If the weight value of the current edge is large, let cmp=1;
            cmp = 1;
        }else if (this.weight()<that.weight()){
            //If the weight value of the current edge is small, let cmp=-1;
            cmp=-1;
        }else{
            //If the weight value of the current edge is as large as that edge, let cmp=0
            cmp = 0;
        }
        return cmp;
    }
}

3.2 implementation of weighted undirected graph

We have completed the undirected graph before. Based on the undirected graph, we only need to switch the representation of edges to Edge objects.
API design:

Class name	EdgeWeightedGraph
Construction method	EdgeWeightedGraph(int V): creates an empty weighted undirected graph with V vertices
Member method	1.public int V(): get the number of vertices in the graph 2.public int E(): get the number of edges in the graph 3.public void addEdge(Edge e): add an edge e to the weighted undirected graph 4.public Queue adj(int v): get all edges associated with vertex v 5.public Queue edges(): get all edges of the weighted undirected graph
Member variable	1.private final int V: record the number of vertices 2.private int E: number of recording edges 3.private Queue[] adj: adjacency table

code:

public class EdgeWeightedGraph {
    //Total number of vertices
    private final int V;
    //Total number of edges
    private int E;
    //Adjacency table
    private Queue<Edge>[] adj;

    //Create a null weighted undirected graph with V vertices
    public EdgeWeightedGraph(int V) {
        //Number of initialization vertices
        this.V = V;
        //Number of initialization edges
        this.E = 0;
        //Initialize adjacency table
        this.adj = new Queue[V];
        for (int i = 0; i < adj.length; i++) {
            adj[i] = new Queue<Edge>();
        }
    }

    //Gets the number of vertices in the graph
    public int V() {
        return V;
    }

    //Gets the number of edges in the graph
    public int E() {
        return E;
    }

    //Add an edge to the weighted undirected graph e
    public void addEdge(Edge e) {
        //You need to make edge e appear in the adjacency table of two vertices of edge e at the same time
        int v = e.either();
        int w = e.other(v);

        adj[v].enqueue(e);
        adj[w].enqueue(e);

        //Number of sides + 1
        E++;
    }

    //Gets all edges associated with the vertex v
    public Queue<Edge> adj(int v) {
        return adj[v];
    }

    //Gets all edges of a weighted undirected graph
    public Queue<Edge> edges() {

        //Create a queue object to store all the edges
        Queue<Edge> allEdges = new Queue<>();

        //Traverse each vertex in the graph and find the adjacency table of the vertex, which stores each edge associated with the vertex

        //Because this is an undirected graph, the same edge appears in the adjacency table of its associated two vertices at the same time. It is necessary to record an edge only once;
        for(int v =0;v<V;v++){
            //Traverse the adjacency table of v vertices and find each edge associated with v
            for (Edge e : adj(v)) {

                if (e.other(v)<v){
                    allEdges.enqueue(e);
                }

            }
        }
        return allEdges;
    }
}

4, Minimum spanning tree

In the previously learned weighted graph, we found that its edges are associated with a weight, so we can solve the minimum cost problem according to this weight, but how can we find the vertices and edges corresponding to the minimum cost? The minimum spanning tree correlation algorithm can be solved.

4.1 definition of minimum spanning tree and related conventions

definition:
The spanning tree of a graph is an acyclic connected subgraph containing all its vertices, the minimum spanning tree of a weighted undirected graph, and its spanning tree with the minimum weight (the sum of the weights of all edges in the tree)

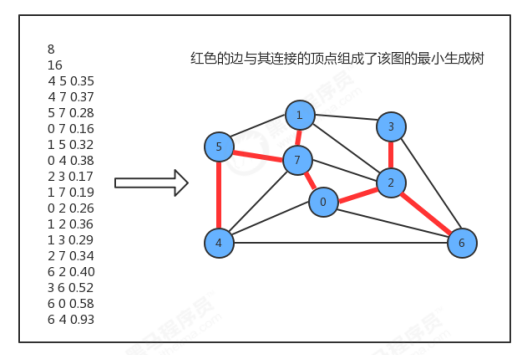
appointment:
Only connected graphs are considered. The definition of minimum spanning tree shows that it can only exist in connected graphs. If the graph is not connected, the minimum spanning tree of each connected graph subgraph is calculated separately and merged together, which is called minimum spanning forest.

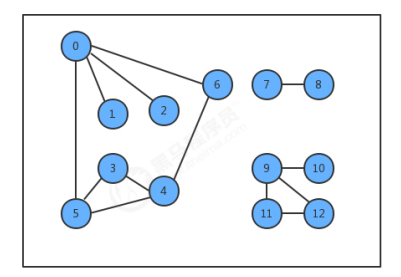
All edges have different weights. If the weights of different edges can be the same, the minimum spanning tree of a graph may not be unique. Although our algorithm can deal with this situation, for better understanding, we agree that the weights of all edges are different.

4.2 minimum spanning tree principle

4.2. 1 Properties of trees

1. Connecting any two vertices in the tree with an edge will produce a new ring;
   
2. Deleting any edge from the tree will get two independent trees;
   

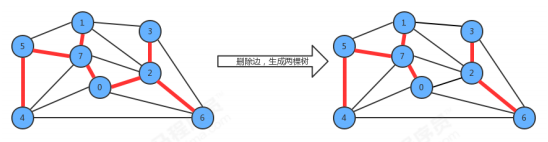
4.2. 2 segmentation theorem

To find the minimum spanning tree of a connected graph, we need to complete it by segmentation theorem.
Segmentation:
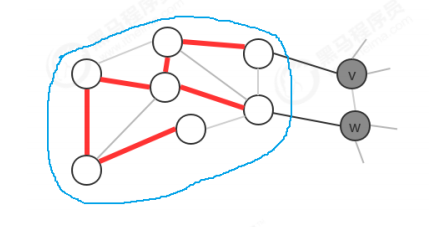
All vertices of a graph are divided into two non empty sets without intersection according to some rules.
Cross cutting edge:
An edge connecting two vertices belonging to different sets is called a crosscutting edge.
For example, if we divide the vertices in the graph into two sets, gray vertices belong to one set and white vertices belong to another set, the effect is as follows:

Segmentation theorem:
In a weighted graph, given any segmentation, the least weight of its cross cutting edge must belong to the minimum spanning tree in the graph.

Note: among the multiple crosscutting edges generated by one segmentation, the edge with the smallest weight may not be the only edge belonging to the minimum spanning tree of the graph.

4.3 greedy algorithm

Greedy algorithm is the basic algorithm to calculate the minimum spanning tree of graph. Its basic principle is the segmentation theorem. Use the segmentation theorem to find one edge of the minimum spanning tree and repeat until all edges of the minimum spanning tree are found. If a graph has V vertices, it needs to find V-1 edges to represent the minimum spanning tree of the graph.

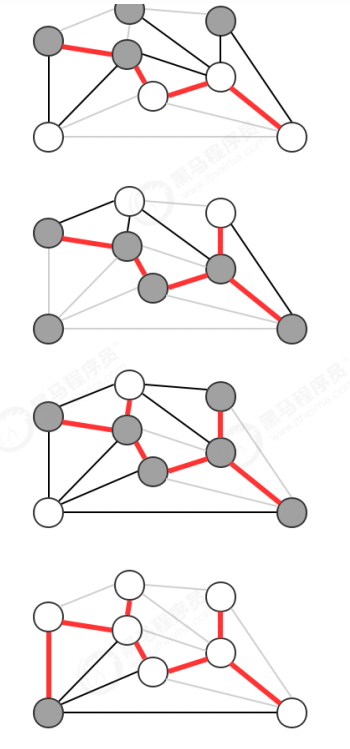
There are many algorithms to calculate the minimum spanning tree of a graph, but these algorithms can be regarded as a special case of greedy algorithms. The difference between these algorithms is the way to save the segmentation and determine the cross cutting edge with the minimum weight.

4.4 Prim algorithm

We learn the first method to calculate the minimum spanning tree, called Prim algorithm, which adds an edge to a spanning tree at each step. At first, the tree has only one vertex, and then V-1 edges will be added to it. Each time, the next edge with the lowest weight connecting the vertex in the tree and the vertex not in the tree will be added to the tree.
Segmentation rules of Prim algorithm:
The vertices in the minimum spanning tree are regarded as a set, and the vertices not in the minimum spanning tree are regarded as another set.

4.4. 1. API design of prim algorithm

Class name	PrimMST
Construction method	PrimMST(EdgeWeightedGraph G): create a minimum spanning tree calculation object according to a weighted undirected graph;
Member method	1.private void visit(EdgeWeightedGraph G, int v): add vertex v to the minimum spanning tree and update the data 2.public Queue edges(): get all edges of the minimum spanning tree
Member variable	1.private Edge[] edgeTo: the index represents the vertex, and the value represents the shortest edge between the current vertex and the minimum spanning tree 2.private double[] distTo: the index represents the vertex, and the value represents the weight of the shortest edge between the current vertex and the minimum spanning tree 3.private boolean[] marked: the index represents the vertex. If the current vertex is already in the tree, the value is true; otherwise, it is false 4.private IndexMinPriorityQueue pq: store valid crosscutting edges between vertices in the tree and non vertices in the tree

4.4. 2 implementation principle of prim algorithm

Prim algorithm always divides the vertices in the graph into two sets, the minimum spanning tree vertex and the non minimum spanning tree vertex. By constantly repeating some operations, you can gradually add the vertices in the non minimum spanning tree to the minimum spanning tree until all the vertices are added to the minimum spanning tree.

When designing the API, we use the minimum index priority queue to store the effective crosscutting edges of vertices in the tree and non vertices in the tree. How is it represented? We can let the index value of the minimum index priority queue represent the vertices of the graph, and let the value in the minimum index priority queue represent the edge weight from another vertex to the current vertex.

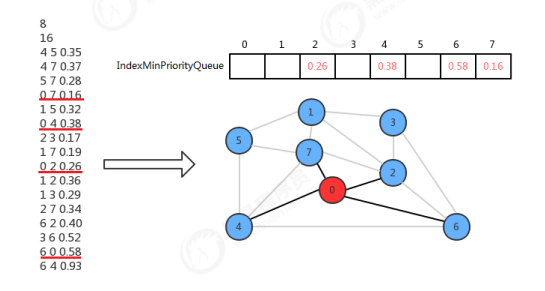
In the initialization state, 0 is the only vertex in the minimum spanning tree by default, and other vertices are not in the minimum spanning tree. At this time, the crosscutting edge is the four edges 0-2,0-4,0-6,0-7 in the adjacency table of vertex 0. We only need to store the weight values of these edges at the indexes 2, 4, 6 and 7 of the index priority queue.

Now you just need to find the edge with the least weight from the four crosscutting edges, and then add the corresponding vertices. Therefore, the weight of the crosscutting edge 0-7 is the smallest. Therefore, the edge 0-7 is added. At this time, 0 and 7 belong to the vertex of the minimum spanning tree, and the others do not. Now the edge in the adjacent table of vertex 7 also becomes the crosscutting edge. At this time, two operations need to be done:

1. The 0-7 edge is no longer a crosscutting edge and needs to be invalidated:
   You only need to call the delMin() method of the minimum index priority queue to complete it;
2. 2 and 4 vertices each have two connections pointing to the minimum spanning tree, and only one needs to be reserved:
   The weight of 4-7 is less than that of 0-4, so keep 4-7 and call change(4,0.37) of the index priority queue,
   The weight of 0-2 is less than that of 2-7, so keep 0-2 and no additional operation is required.
   

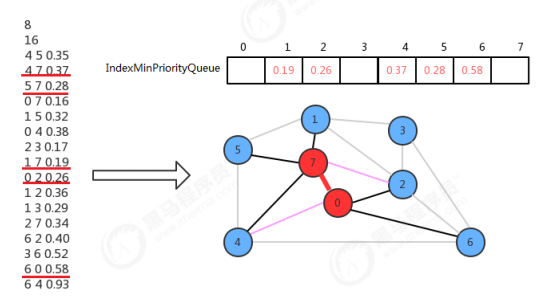
By repeating the above actions, we can add all vertices to the minimum spanning tree.

4.4. 3 code

public class PrimMST {
    //The index represents the vertex, and the value represents the shortest edge between the current vertex and the minimum spanning tree
    private Edge[] edgeTo;
    //The index represents the vertex, and the value represents the weight of the shortest edge between the current vertex and the minimum spanning tree
    private double[] distTo;
    //The index represents the vertex. If the current vertex is already in the tree, the value is true; otherwise, it is false
    private boolean[] marked;
    //Stores valid crosscutting edges between vertices in the tree and non vertices in the tree
    private IndexMinPriorityQueue<Double> pq;

    //According to a weighted undirected graph, the minimum spanning tree calculation object is created
    public PrimMST(EdgeWeightedGraph G) {
       //Initialize edgeTo
        this.edgeTo = new Edge[G.V()];
        //Initialize distTo
        this.distTo = new double[G.V()];
        for (int i = 0; i < distTo.length; i++) {
            distTo[i] = Double.POSITIVE_INFINITY;
        }
        //Initialize marked
        this.marked = new boolean[G.V()];
        //Initialize pq
        pq = new IndexMinPriorityQueue<Double>(G.V());

        //By default, vertex 0 is allowed to enter the tree, but there is only one vertex 0 in the tree. Therefore, vertex 0 is not connected to other vertices by default, so let the value at the corresponding position of distTo store 0.0
        distTo[0] = 0.0;
        pq.insert(0,0.0);

        //Traverse the index minimum priority queue, get the vertex corresponding to the minimum and N cutting edges, and add the vertex to the minimum spanning tree
        while (!pq.isEmpty()){
            visit(G,pq.delMin());
        }
    }

    //Add vertex v to the minimum spanning tree and update the data
    private void visit(EdgeWeightedGraph G, int v) {
        //Add vertex v to the minimum spanning tree
        marked[v] = true;
        //Update data
        for (Edge e : G.adj(v)) {
            //Get another vertex of edge e (current vertex is v)
            int w = e.other(v);
            //Judge whether another vertex is already in the tree. If it is in the tree, no processing will be done. If it is no longer in the tree, the data will be updated
            if (marked[w]){
                continue;
            }


            //Judge whether the weight of edge e is less than the weight from w vertex to the smallest edge already existing in the tree;
            if (e.weight()<distTo[w]){
                //Update data
                edgeTo[w] = e;

                distTo[w] = e.weight();

                if (pq.contains(w)){
                    pq.changeItem(w,e.weight());
                }else{
                    pq.insert(w,e.weight());
                }
            }
        }
    }

    //Gets all edges of the minimum spanning tree
    public Queue<Edge> edges() {
        //Create queue object
        Queue<Edge> allEdges = new Queue<>();
        //Traverse the edgeTo array to get each edge. If it is not null, it will be added to the queue
        for (int i = 0; i < edgeTo.length; i++) {
            if (edgeTo[i]!=null){
                allEdges.enqueue(edgeTo[i]);
            }
        }
        return allEdges;
    }
}

4.5 kruskal algorithm

kruskal algorithm is another algorithm to calculate the minimum spanning tree of a weighted undirected graph. Its main idea is to deal with them according to the weight of edges (from small to large). The edges are added to the minimum spanning tree. The added edges will not form a ring with the edges that have been added to the minimum spanning tree until the tree contains V-1 edges.
Differences between kruskal algorithm and prim algorithm:
Prim algorithm constructs the minimum spanning tree one by one, and adds an edge to a tree at each step. kruskal algorithm constructs the minimum spanning tree side by side, but its segmentation rules are different. Every time it looks for the edge, it will connect two trees in a forest. If a weighted undirected graph is composed of V vertices, and each vertex forms an independent tree under initialization, then the V vertices correspond to V trees to form a forest. kruskal algorithm will merge the two trees into one tree every time until there is only one tree left in the whole forest.

4.5. 1. Kruskal algorithm API design

Class name	KruskalMST
Construction method	KruskalMST(EdgeWeightedGraph G): create a minimum spanning tree calculation object according to a weighted undirected graph;
Member method	1.public Queue edges(): get all edges of the minimum spanning tree
Member variable	1.private Queue mst: save all edges of the minimum spanning tree 2.private UF_Tree_Weighted uf: the index represents the vertex, using UF Connect (V, w) can judge whether vertex v and vertex W are in the same tree. Use UF Union (V, w) can merge the tree of vertex v and the tree of vertex W 3.private MinPriorityQueue pq: store all edges in the graph, use the minimum priority queue, and sort the edges according to weight

4.5. 2. Implementation principle of Kruskal algorithm

When designing the API, a MinPriorityQueue pq is used to store all edges in the graph, and PQ is used each time Delmin () takes out the edge with the smallest weight and obtains the two vertices V and W associated with the edge, through UF Connect (V, w) determines whether V and W are connected. If connected, it proves that the two vertices are in the same tree, so this edge can no longer be added to the minimum spanning tree, because adding an edge to any two vertices of a tree will form a ring, and the minimum spanning tree cannot have a ring. If not connected, it is through UF Connect (V, w) combines the tree of vertex v and the tree of vertex W into a tree, and adds this edge to the mst queue. In this way, if all edges are processed, all the edges of the minimum spanning tree will be stored in the mst.

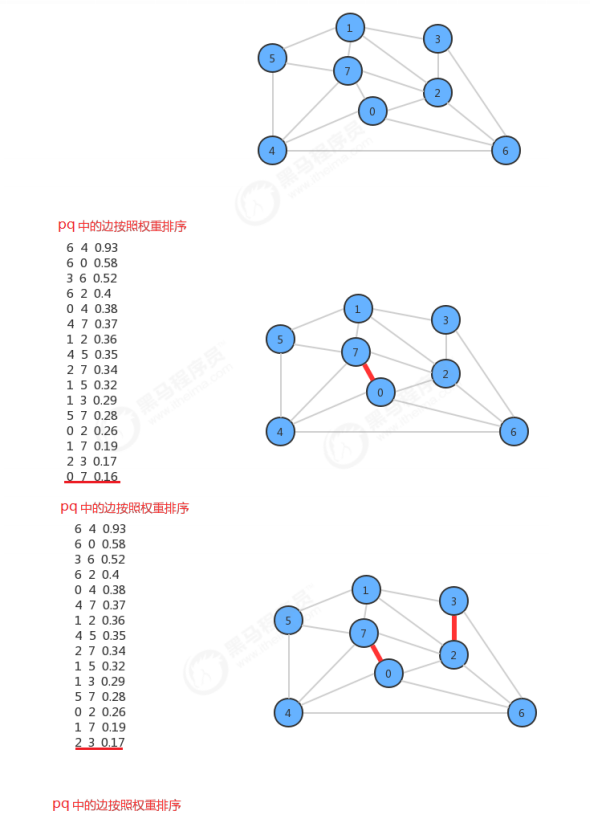
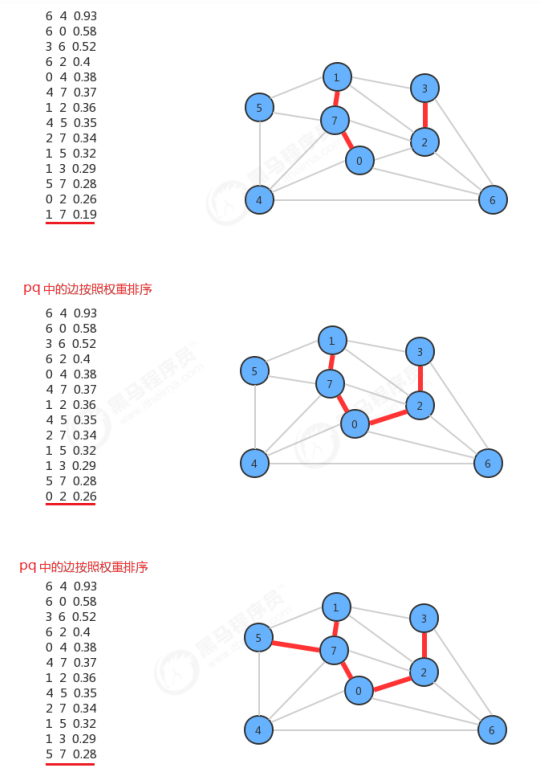
4.5. 3 code

public class KruskalMST {
    //Save all edges of the minimum spanning tree
    private Queue<Edge> mst;
    //The index represents the vertex, using UF Connect (V, w) can judge whether vertex v and vertex W are in the same tree. Use UF Union (V, w) can merge the tree of vertex v and the tree of vertex W
    private UF_Tree_Weighted uf;
    //All edges in the graph are stored, and the edges are sorted by weight using the minimum priority queue
    private MinPriorityQueue<Edge> pq;

    //According to a weighted undirected graph, the minimum spanning tree calculation object is created
    public KruskalMST(EdgeWeightedGraph G) {
        //Initialize mst
        this.mst = new Queue<Edge>();
        //Initialize uf
        this.uf = new UF_Tree_Weighted(G.V());
        //Initialize pq
        this.pq = new MinPriorityQueue<>(G.E()+1);
        //Store all the edges in the graph in pq
        for (Edge e : G.edges()) {
            pq.insert(e);
        }

        //Traverse the pq queue, get the edge with the minimum weight, and process it
        while(!pq.isEmpty() && mst.size()<G.V()-1){
            //Find the edge with the least weight
            Edge e = pq.delMin();
            //Find the two vertices of the edge
            int v = e.either();
            int w = e.other(v);

            //Judge whether the two vertices are already in the same tree. If they are in the same tree, the edge will not be processed. If they are not in the same tree, the two trees to which the two vertices belong will be merged into one tree
            if (uf.connected(v,w)){
                continue;
            }

            uf.union(v,w);

            //Get edge e into mst queue
            mst.enqueue(e);
        }
    }

    //Gets all edges of the minimum spanning tree
    public Queue<Edge> edges() {
        return mst;
    }
}

5, Weighted directed graph

In the previously learned weighted undirected graph, the edge has no direction, and the same edge will appear in the adjacency table of two vertices of the edge at the same time. In order to deal with the problem of directional graphs, we need to implement the following weighted directed graphs.

5.1 representation of edges of weighted digraph

API design:

Class name	DirectedEdge
Construction method	DirectedEdge(int v,int w,double weight): construct an edge object from vertices v and W and weight values
Member method	1.public double weight(): get the weight value of the edge 2.public int from(): get the starting point of the directed edge 3.public int to(): get the end point of the directed edge
Member variable	1.private final int v: starting point 2.private final int w: end point 3.private final double weight: the weight of the current edge

code:

public class DirectedEdge {
    private final int v;//starting point
    private final int w;//End
    private final double weight;//The weight of the current edge

    //Construct an edge object from vertices v and w and weight values
    public DirectedEdge(int v, int w, double weight) {
        this.v = v;
        this.w = w;
        this.weight = weight;
    }

    //Gets the weight value of the edge
    public double weight(){
        return weight;
    }

    //Gets the start point of the directed edge
    public int from(){
        return v;
    }

    //Gets the end point of the directed edge
    public int to(){
        return w;
    }
}

5.2 implementation of weighted directed graph

We have completed the directed graph before. Based on the directed graph, we only need to switch the representation of edges to DirectedEdge objects.
API design:

Class name	EdgeWeightedDigraph
Construction method	EdgeWeightedDigraph(int V): create an empty weighted digraph with V vertices
Member method	1.public int V(): get the number of vertices in the graph 2.public int E(): get the number of edges in the graph 3.public void addEdge(DirectedEdge e): add an edge e to the weighted directed graph 4.public Queue adj(int v): obtain all edges indicated by vertex v 5.public Queue edges(): get all edges of the weighted digraph
Member variable	1.private final int V: record the number of vertices 2.private int E: number of recording edges 3.private Queue[] adj: adjacency table

code:

public class EdgeWeightedDigraph {
    //Total number of vertices
    private final int V;
    //Total number of edges
    private int E;
    //Adjacency table
    private Queue<DirectedEdge>[] adj;

    //Create a null weighted directed graph with V vertices
    public EdgeWeightedDigraph(int V) {
        //Number of initialization vertices
        this.V = V;
        //Number of initialization edges
        this.E = 0;
        //Initialize adjacency table
        this.adj = new Queue[V];

        for (int i = 0; i < adj.length; i++) {
            adj[i] = new Queue<DirectedEdge>();
        }
    }

    //Gets the number of vertices in the graph
    public int V() {
        return V;
    }

    //Gets the number of edges in the graph
    public int E() {
        return E;
    }

    //Add an edge to the weighted directed graph e
    public void addEdge(DirectedEdge e) {
        //Edge e has a direction, so you only need to make e appear in the adjacency table of the starting point
        int v = e.from();
        adj[v].enqueue(e);
        E++;
    }

    //Gets all edges indicated by vertex v
    public Queue<DirectedEdge> adj(int v) {
        return adj[v];
    }

    //Gets all edges of a weighted directed graph
    public Queue<DirectedEdge> edges() {
        //Traverse each vertex in the graph to get the adjacency table of the vertex, traverse each edge, add it to the queue and return
        Queue<DirectedEdge> allEdges = new Queue<>();
        for (int v = 0;v<V;v++){
            for (DirectedEdge edge : adj[v]) {
                allEdges.enqueue(edge);
            }
        }
        return allEdges;
    }
}

6, Shortest path

After having a weighted directed graph, we can immediately think of the use scenarios in real life. For example, in a map, we can find the path between vertex A and location b. this path can be the shortest distance, the shortest time, or the least cost. If we regard distance / time / cost as cost, Then we need to find the path with the lowest cost between location a and location b, that is, the shortest path problem we need to solve next.

6.1 definition and nature of shortest path

definition:
In a weighted directed graph, the shortest path from vertex s to vertex t is the path with the lowest total weight among all paths from vertex s to vertex t.
nature:

1. The path is directional;
2. Weight is not necessarily equivalent to distance. The weight can be distance, time, cost, etc. the smallest weight refers to the lowest cost
3. Only connected graphs are considered. Not all vertices in a graph are reachable. If s and t are not reachable, there is no shortest path between them,
   In order to simplify the problem, only connected graphs are considered here.
4. The shortest path is not necessarily unique. There may be many paths with the least weight from one vertex to another. Here, you only need to find one.

Shortest path tree:
Given a weighted directed graph and a vertex s, a shortest path tree starting from s is a subgraph of the graph, which contains vertex s and all vertices reachable from S. The root node of the directed tree is s, and each path of the tree is the shortest path in the directed graph.

6.2 shortest path tree API design

The classic algorithm for calculating the shortest path tree is dijstra algorithm. In order to realize it, the following API is designed:

Class name	DijkstraSP
Construction method	public DijkstraSP(EdgeWeightedDigraph G, int s): create a shortest path tree object with vertex s calculated according to a pair of weighted digraph G and vertex s
Member method	1.private void relax(EdgeWeightedDigraph G, int v): relax vertex v in graph G 2.public double distTo(int v): get the total weight of the shortest path from vertex s to vertex v 3.public boolean hasPathTo(int v): judge whether it is reachable from vertex s to vertex v 4.public Queue pathTo(int v): query all edges in the shortest path from the starting point s to the vertex v
Member variable	1.private DirectedEdge[] edgeTo: the index represents the vertex, and the value represents the last edge on the shortest path from vertex s to the current vertex 2.private double[] distTo: the index represents the vertex, and the value is the total weight of the shortest path from vertex s to the current vertex 3.private IndexMinPriorityQueue pq: store valid crosscutting edges between vertices in the tree and non vertices in the tree

6.3 relaxation technology

The word relaxation comes from life: a rubber band is tightly expanded along a path between two vertices. If there is more than one path between the two vertices and there is a shorter path, the rubber band can be relaxed by transferring the rubber band to a shorter path.

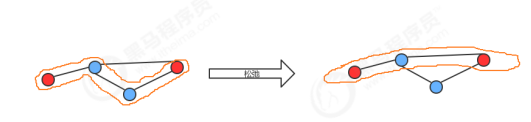
The simple principle of relaxation can be used to calculate the shortest path tree.
In our API, we need to use two member variables edgeTo and distTo to to store edges and weights respectively. At first, given a graph G and vertex s, we only know the edges of the graph and the weights of these edges, and we know nothing else. At this time, the total weight disto[s]=0 of the shortest path from vertex s to vertex s; The total weight from vertex s to other vertices is infinite by default. With the implementation of the algorithm, the relaxation technology is continuously used to process the edges and vertices of the graph, and the data in edgeTo and distTo are updated according to certain conditions. Finally, the shortest path stiffness tree can be obtained.

Edge relaxation:
Relaxing edge v - > W means checking whether the shortest path from s to w starts from s to v and then from v to w?

If yes, the v-w edge needs to be added to the shortest path tree to update the contents in edgeTo and distTo: edgeTo[w] = DirectedEdge object representing the V - > W edge, distTo [w] = distTo [v] + V - > W edge weight;

If not, the edge V - > W is ignored.

Relaxation of vertices:
The relaxation of vertices is based on the relaxation of edges. Only relax all the edges pointed out by a vertex, then the vertex is relaxed. For example, to relax vertex v, you only need to traverse the adjacency table of V and relax each edge, then vertex v is relaxed.

If the starting point is set to vertex 0, the process of finding the shortest path 0 - > 2 - > 7 > 3 - > 6 from starting point 0 to vertex 6 is as follows:

6.4 Dijstra algorithm implementation

The implementation of Disjstra algorithm is very similar to Prim algorithm. Each step of constructing the shortest path tree is to add a new edge to the tree, which is the edge with the least weight in the effective crosscutting edge pq queue.

public class DijkstraSP {
    //The index represents the vertex, and the value represents the last edge on the shortest path from vertex s to the current vertex
    private DirectedEdge[] edgeTo;
    //The index represents the total weight of the shortest path from vertex s to the current vertex
    private double[] distTo;
    //Stores valid crosscutting edges between vertices in the tree and non vertices in the tree
    private IndexMinPriorityQueue<Double> pq;

    //According to a pair of weighted digraph G and vertex s, a shortest path tree object with vertex s is created
    public DijkstraSP(EdgeWeightedDigraph G, int s){
        //Initialize edgeTo
        this.edgeTo = new DirectedEdge[G.V()];
        //Initialize distTo
        this.distTo = new double[G.V()];
        for (int i = 0; i < distTo.length; i++) {
            distTo[i] = Double.POSITIVE_INFINITY;
        }
        //Initialize pq
        this.pq = new IndexMinPriorityQueue<>(G.V());

        //Find the shortest path tree starting from vertex s in Figure G

        //By default, let vertex s enter the shortest path tree
        distTo[s] = 0.0;
        pq.insert(s,0.0);

        //Traversal pq

        while(!pq.isEmpty()){
            relax(G,pq.delMin());
        }
    }

    //Vertex v in relaxed graph G
    private void relax(EdgeWeightedDigraph G, int v){

        for (DirectedEdge edge : G.adj(v)) {
            //Gets the end point w of the edge
            int w = edge.to();

            //Through the relaxation technique, it is determined whether the shortest path from the starting point s to the vertex w needs to be from the vertex s to the vertex v, and then from the vertex v to the vertex W
            if (distTo(v)+edge.weight()<distTo(w)){
                distTo[w] = distTo[v]+edge.weight();
                edgeTo[w] = edge;

                //Judge whether the vertex w already exists in pq. If so, update the weight. If not, add it directly
                if (pq.contains(w)){
                    pq.changeItem(w,distTo(w));
                }else{
                    pq.insert(w,distTo(w));
                }
            }
        }
    }

    //Gets the total weight of the shortest path from vertex s to vertex v
    public double distTo(int v){
        return distTo[v];
    }

    //Judge whether it is reachable from vertex s to vertex v
    public boolean hasPathTo(int v){
        return distTo[v]<Double.POSITIVE_INFINITY;
    }

    //Query all edges in the shortest path from the starting point s to the vertex v
    public Queue<DirectedEdge> pathTo(int v){
        //Judge whether it is reachable from vertex s to vertex v. if not, return null directly
        if (!hasPathTo(v)){
            return null;
        }

        //Create queue object
        Queue<DirectedEdge> allEdges = new Queue<>();

        while (true){
            DirectedEdge e = edgeTo[v];
            if (e==null){
                break;
            }

            allEdges.enqueue(e);

            v = e.from();
        }
        return allEdges;
    }
}