catalogue
Search algorithm can also be called search algorithm. It is to find a specific number from an ordered sequence. It is often used to judge whether a number is in the sequence or the position of a number in the sequence. In computer applications, search is a common basic operation and an important part of the algorithm.
The search sequence can be divided into static search and dynamic search according to the operation mode. Static search only finds specific numbers in the sequence without any modification (sorting). Therefore, in addition to whether a specific number exists or not, the static search can also return the serial number (subscript) of the specific number in the current sequence. Dynamic lookup inserts or deletes while searching. Therefore, dynamic lookup can only return whether a specific number exists in the current sequence.
1. Sequential search
principle
Sequential search is the simplest and most direct search algorithm. Sequential search is to search the sequence from beginning to end. It is the least technical and easiest to understand algorithm.
Sequential lookups are static lookups. Because the sequential search is to find a specific number from beginning to end, you can also start the search directly without sorting the number sequence. In order to unify the style, an ordered sequence is adopted here. Take the iList sequence as an example. In the worst case of sequential search, you need to search len(iList) times to find the target or confirm that there is no target in the sequence.
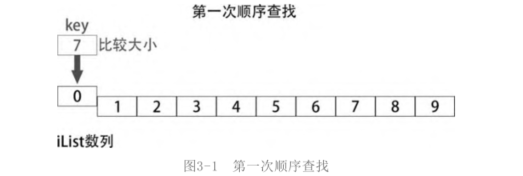
First find
Start from the first number of the list of ilinist numbers (ilinist [0]) and compare whether the numbers found are equal. If equal, return the subscript of the number and exit, otherwise compare the next number in the sequence,
The nth search
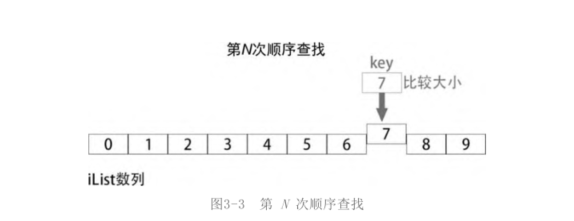
After the nth search, an element equal to the key is finally found in the sequence, and the subscript of this element is returned (in actual use, it is possible for 0, 1 or more elements in the sequence to be equal to the key. Multiple elements are excluded here).
code
To generate a random number list, we use a function and then import it for use.
#!/user/bin/env/python3
#-*-conding:utf-8 -*-
# data:20211210
# author:yang
import random
def randomList(n):
"""Returns a length of n List of integers in the range of[0,1000)"""
iList = []
for i in range(n):
iList.append(random.randrange(1000))
return iList
if __name__=="__main__":
iList = randomList(10)
print("iList:",iList)#!/user/bin/env/python3
#-*-conding:utf-8 -*-
# data:202112112
# author:yang
import random
from randomList import randomList
import timeit
def sequentialSearch(iList,key):
iLen = len(iList)
for i in range(iLen):
if iList[i] == key:
return i
return -1
if __name__ == "__main__":
iList = randomList(10)
print("iList:",iList)
keys = [random.choice(iList),random.randrange(min(iList),max(iList))]
for key in keys:
res = sequentialSearch(iList,key)
if res >= 0:
print("%d is in the list,index is:%d\n"%(key,res))
else:
print("%d is not in the list\n"%key)
Results
expand
1. random.choice()
Definition: the choice() method returns a random item of a list, tuple or string.
Syntax: random choice( seq )
- seq -- can be a list, tuple or string.
2. random.randrange()
Definition: the random number () method returns a random number in the specified incremental cardinality set. The default cardinality value is 1.
Syntax: random randrange ([start,] stop [,step])
- Start -- the start value within the specified range, which is included in the range.
- stop -- the end value within the specified range, which is not included in the range.
- step -- specifies the incremental cardinality.
Conclusion: this method is very basic and the efficiency is too slow.
2. Dichotomy
principle
Searching for a specific number in an ordered sequence is undoubtedly the most inefficient method. Directly find the number in the middle of the sequence and compare it with the searched number (key). If this number is smaller than the number to be searched (key), there is no doubt that the number to be searched must be in the second half of the ordered sequence; Otherwise, the number to be searched must be in the first half of the ordered sequence. Next, take the list of Iist numbers (numbers 0 to 9) as an example, and assume that the number key to be searched is 9.
First find
The length of iList is len(iList)=10. The middle element subscript is the sum of the subscript (0) of the first element of the sequence and the subscript (9) of the tail element of the sequence divided by 2, (0 + 9) / / 2 = 4. iList[mid] is iList[4], and the first comparison is with iList[4], as shown in the figure
As shown in.
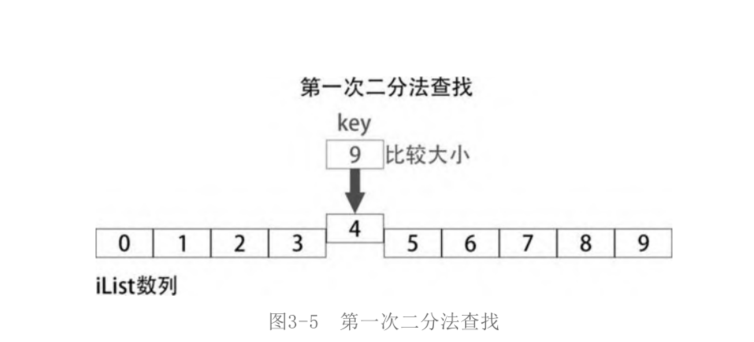
Obviously, the key is larger than iList[4], so the key must be in the second half of iList[4].
Second lookup
The subscript of the middle element in the second half is (5 + 10) / / 2 = 7, so iList[mid] is iList[7]. The second comparison is between key and iList[7], as shown in the figure.
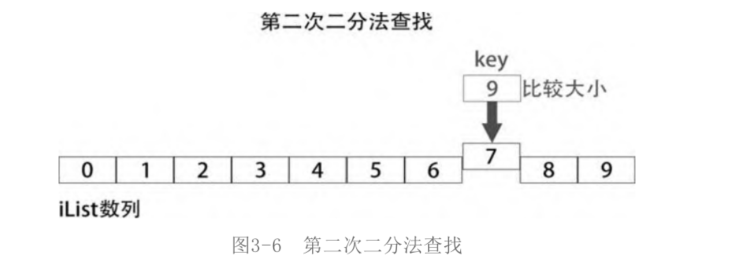
The key is larger than iList[7], and the key must be in the second half of iList[7]. The subscript of the middle element in the second half is (8 + 9) / / 2 = 8. At this time, there are only two elements left. It is not worth the loss to use dichotomy to find. Just compare the size of the number directly.
code
#!/user/bin/env/python3
#-*-conding:utf-8 -*-
# data:202112112
# author:yang
import random
from randomList import randomList
import sort
def binarySearch(iList,key):
iLen = len(iList)
left = 0
right = iLen - 1
while right - left > 1:
mid = (left + right)// 2
if key < iList[mid]:
right = mid
elif key > iList[mid]:
left = mid
else:
return mid
if key == iList[left]:
return left
if key == iList[right]:
return right
else:
return -1
if __name__ == "__main__":
iList = sort.quickSort(randomList(10))
print("iList2:",iList)
keys = [random.choice(iList),random.randrange(min(iList),max(iList))]
for key in keys:
res = binarySearch(iList,key)
if res >= 0:
print("%d is in the list,index is %d.\n"%(key,res))
else:
print("%d is not in the list.\n"%key)
result
Note: sort Py (quick sort algorithm)
#!/user/bin/env/python3
#-*-conding:utf-8 -*-
# data:20211210
# author:yang
from randomList import randomList
import timeit
def quickSort(iList):
if len(iList) <= 1:
return iList
left = []
right = []
for i in iList[1:]:
if i <= iList[0]:
left.append(i)
else:
right.append(i)
return quickSort(left) + [iList[0]] + quickSort(right)
if __name__ == "__main__":
iList = randomList(10)
print(iList)
print(quickSort(iList))
# print(timeit.timeit("selectionSort(iList)","from __main__ import selectionSort,iList",number = 1))
Summary: it is the same to find the number 9. The sequential search needs to be found for the 10th time (this is the worst case of sequential search), while the dichotomy search only needs 3 times (this is also the worst case). Obviously, the efficiency of dichotomy search is higher than that of sequential search.
Remember: it's only possible if you're in good order.
3. Fibonacci search
Fibonacci sequence, also known as the golden section sequence, refers to such a sequence: 1,1,2,3,5,8,13,21. Mathematically, Fibonacci is defined by the recursive method as follows: F (1)=1, F (2)=1, f (n) = f (n - 1) + F (n-2) (n ≥ 2). The later the sequence, the more the ratio of two adjacent numbers tends to the golden ratio value (0.618). Fibonacci search is divided according to Fibonacci sequence on the basis of dichotomy search.
principle
Fibonacci search is almost the same as dichotomy search, except that the position of the comparison point (reference point) is different. The dichotomy selects the element in the middle of the sequence as the comparison point (reference point), while Fibonacci search selects the position of the slightly backward point in the middle of the sequence as the comparison point, that is, the golden section point. Assuming that the length of the searched sequence is 1, the comparison point selected by Fibonacci search is at the position of 0.618. This is determined by the characteristics of Fibonacci sequence.
Since it is called Fibonacci lookup, first list a Fibonacci sequence. [1, 2, 3, 5, 8, 13, 21], this Fibonacci sequence only provides the position of the parameter point in the searched sequence, which is basically a subscript. Take iList = [0, 1, 2, 3, 4, 5, 6, 7,8, 9] as an example, there are len(iList)=10 elements. Select a Fibonacci number slightly larger than len(iList), that is, 13. The Fibonacci number smaller than 13 is 8, so the reference point selected for the first time is iList[8] in iList. If the number key to be searched is smaller than iList[8], take a look at the Fibonacci number (5) smaller than 8. The reference point selected for the second time is iList[5]. By analogy, the Fibonacci number is used as the position parameter of the searched sequence.
Take iList as the searched sequence and key=7 as an example to start the search.
First find
The length of the iList is 10, and there is no 10 in the Fibonacci number sequence, so it is assumed that the length of the iList is 13 (13 is the Fibonacci number). The Fibonacci number smaller than 13 is 8. According to the Fibonacci search principle, in fact, the reference point should be the eighth number of iList, that is, iList[7]. For the sake of intuition, the iList[8] is selected here, which is also possible.
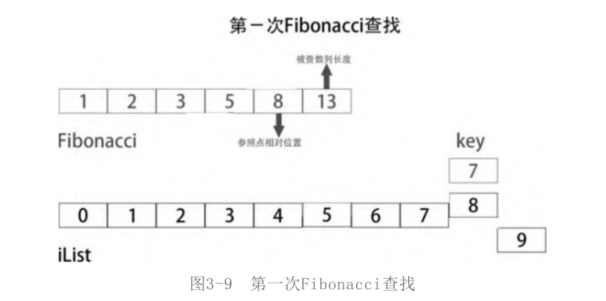
Because the key is smaller than the reference point iList[8], it indicates that the number to be searched is in the front of the iList.
Second lookup
The second search is between iList[0:8]. This time, the length of the searched sequence is 8, and the Fibonacci number one smaller than 8 is 5, so the reference point this time is iList[5].
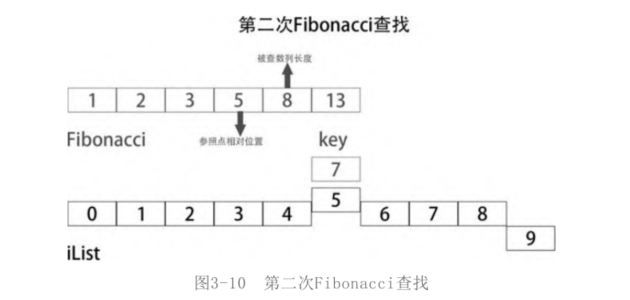
At this time, the key is larger than the iList[5], indicating that the number to be searched is in the second half of the iList[0:8]. That is, between iList[6,8].
Third find
According to the normal process, only iList[6] and iList[7] are left. There is no need to search with Fibonacci. Here we still search according to Fibonacci's scheme. There are only two numbers between iList[6,8], but Fibonacci searches in the sequence composed of three numbers: iList[6], iList[7] and iList[8]. Therefore, the length of the searched sequence is actually 3, so the reference point should be Fibonacci number 2, which is a little smaller than 3. That is, the second number in the searched sequence, iList[7].
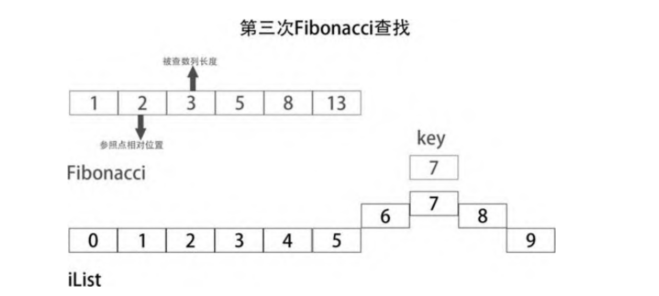
Fibonacci search, as a variant of dichotomy search, is generally more efficient than sequential search, which is comparable to dichotomy. According to the distribution state of data in the sequence, it is difficult to say which is faster between dichotomy and Fibonacci (for example, the number to be searched is just at the front of the sequence, and Fibonacci search efficiency is not as good as dichotomy search).
code
#!/user/bin/env/python3
#-*-conding:utf-8 -*-
# data:202112112
# author:yang
import random
from types import MemberDescriptorType
from warnings import resetwarnings
from randomList import randomList
import sort
def fibonacci(n):
"""return fibonacci The last element of the sequence"""
fList = [1,1]
while n > 1:
fList.append(fList[-1]+fList[-2])
n -= 1
return fList[-1]
def fibonacciSearch(iList,key):
iLen = len(iList)
left = 0
right = iLen - 1
indexSum = 0
k = 1
while fibonacci(k) -1 < iLen -1:
k += 1
while right - left > 1:
mid = left + fibonacci(k-1)
if key < iList[mid]:
right = mid - 1
k -= 1
elif key == iList[mid]:
return mid
else:
left = mid + 1
k -= 2
if key == iList[left]:
return left
elif key == iList[right]:
return right
else:
return -1
if __name__ == "__main__":
iList = sort.quickSort(randomList(10))
print("iList:",iList)
keys = [random.choice(iList),random.randrange(min(iList),max(iList))]
for key in keys:
res = fibonacciSearch(iList,key)
if res >= 0:
print("%d is in the list,index is %d.\n"%(key,res))
else:
print("%d is not in the list.\n"%key)
At fibonacci search Py uses the custom fibonacci function to return a fibonacci number fibonacci(k) through the variable K. The fibonacci(k) returned can be regarded as the length of the searched sequence. fibonacci(k-1) is the "relative position" of the reference point in the searched sequence. At fibonacci search mid = left +fibonacci(k-1) declared in line 36 of Py is the "absolute position" of the reference point in the ilinist sequence, which can be regarded as a list subscript.
4. Interpolation search
When selecting the comparison point (reference point) in the searched sequence, the dichotomy adopts the midpoint and the Fibonacci method adopts the golden section point. Binary search method is the most intuitive. Fibonacci search method may be the most "beautiful", but it is not the most scientific. So, if
How to choose the most scientific comparison point (reference point)? Usually, the searched sequence is not equal difference, and the difference distribution state of the sequence is not known. It is impossible to determine which point to choose is the "optimal solution". The interpolation algorithm gives the most scientific comparison point (reference point) in theory in most cases.
principle
Take the English dictionary as an example. If you want to find a word that begins with a. Generally, it will not start from the middle position (binary search method), nor from the golden section point (number of pages) × 0.618). Intuitively, you should start at the front of the dictionary. However, mathematics has no intuition. It will tell us mid = left + (key -iList[left]) * (right - left) / / (iList[right] - iList[left]). No matter which letter begins the word or any number in any number sequence, this point is the best comparison point in most cases.
First find
Take iList as the searched sequence and key=7 as an example to start the search. Current iList = range(0,10) = [0, 1, 2, 3, 4, 5, 6, 7, 8,9], which is an arithmetic sequence with a difference of 1. In the formula given by interpolation search, mid is the comparison point (reference point), left is the subscript at the beginning of the searched sequence, and right is the subscript at the end of the searched sequence, as shown in the figure.
The first search found the number of searched. Interpolation search may be the fastest algorithm when searching for an equal difference sequence.
Second lookup
Let's take another look at the search of the equal ratio sequence. Reset ilinist = [pow (2, I) for I in range (0, 10)], that is, ilinist = [1, 2, 4, 8, 16, 32, 64, 128256, 512]. The current Iist is an isometric sequence with a ratio of 2. Set key = 128 and start searching in the Iist, as shown in the figure.
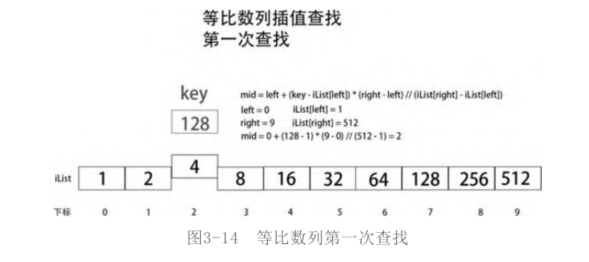
If the target is not found in the first search, search again in the sequence iList[mid, right], that is, move the left right to the position of the current mid, and then recalculate the mid to determine the comparison point (reference point), as shown in the figure
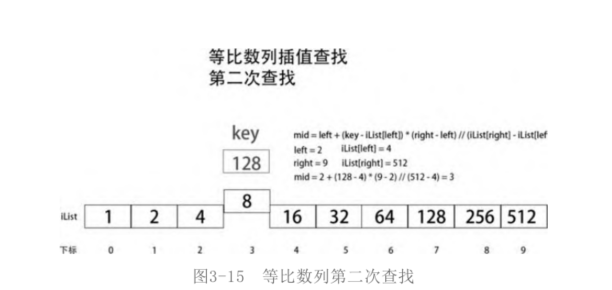
If the target is still not found the second time, move the left right to the current mid position and continue the next search. This time mid= 3 + (128 – 8) * (9 – 3) / / (512 – 8) = 4. Each mid moves only one element to the right. At this speed, the efficiency is far less than that of dichotomy search and Fibonacci search.
code
#!/user/bin/env/python3
#-*-conding:utf-8 -*-
# data:202112112
# author:yang
import random
from types import MemberDescriptorType
from warnings import resetwarnings
from randomList import randomList
import sort
def insertSearch(iList,key):
iLen = len(iList)
left = 0
right = iLen - 1
while right - left > 1:
mid = left + (key - iList[left]) * (right - left) // (iList[right] - iList[left])
if mid == left:
mid += 1
if key < iList[mid]:
right = mid
elif key > iList[mid]:
left = mid
else:
return mid
if key == iList[left]:
return left
elif key == iList[right]:
return right
else:
return -1
if __name__ == "__main__":
iList = sort.quickSort(randomList(10))
print("iList:",iList)
keys = [random.choice(iList),random.randrange(min(iList),max(iList))]
for key in keys:
res = insertSearch(iList,key)
if res >= 0:
print("%d is in the list,index is %d.\n"%(key,res))
else:
print("%d is not in the list.\n"%key)
When the element distribution of the Iist sequence is relatively large, the comparison point of mid may always be equal to left, resulting in an endless loop. So in insertsearch Lines 24 and 25 of Py need to add a restriction.
Summary:
Interpolation search method is also an advanced algorithm of binary search method. When the elements in the sequence are widely distributed, the effect of insertion search is not very good. The arithmetic sequence is the best.
5. Block search
Block search is different from the above search methods: the sequence of sequential search can be out of order; The sequence of binary search and Fibonacci search must be orderly; Block search is between the two. Blocks need to be ordered, and elements can be unordered.
principle
Block search first divides the sequence into blocks according to a certain value range. Elements within a block can be unordered, but the block must be ordered. What is block order? This means that the smallest element in the block at the back position is larger than the largest element in the block at the front position.
Reset an iList = [9, 17, 13, 5, 2, 26, 7, 23, 29]. At present, the sequence iList is unordered. Set the number to be searched key=26. According to the steps of block search, the first thing to do is to divide the Iist into several blocks, at least into two blocks, otherwise it will be in the same order
It makes no difference. By observing the list of iles, it is found that the largest number of the list is no more than 30. Therefore, the list is divided into three blocks according to the three intervals of 0 ~ 9, 10 ~ 19 and 20 ~ 29 (it is not necessary to divide it in this way, but can also be divided into two blocks, four blocks and five blocks... Select a more convenient value to divide it into blocks)
After the blocks are divided, the blocks are in order. The smallest element 13 in block2 is larger than the largest element 9 in block1. The smallest element 23 in block3 is larger than the largest element 17 in block2. The elements in blocks in block1, block2 and block3 are out of order. After dividing the blocks, start searching.
First find
The first search is to compare the number of keys to be searched with the partition number of blocks (or the largest element in each block) to determine which block the number of keys to be searched belongs to, as shown in the figure.
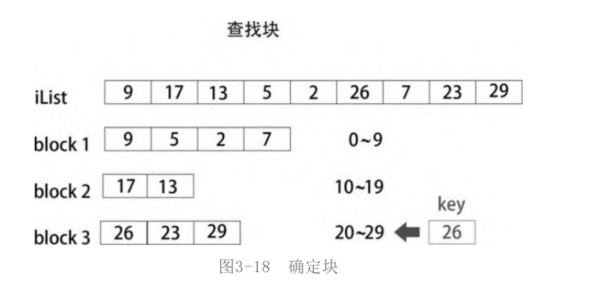
The number of searched key s is larger than the boundary number 19 of block2, so it can only be searched in block3.
Second lookup
The search in the block is to compare one by one, that is, to search in order.
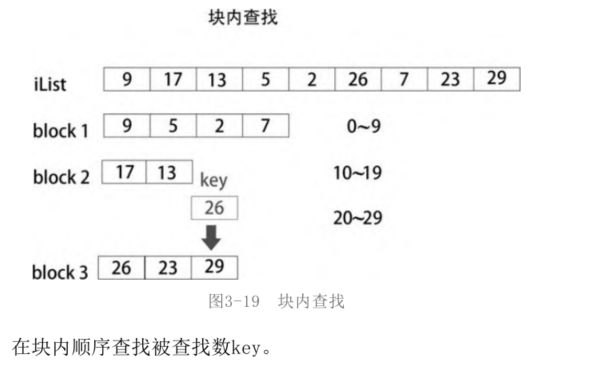
Code
#!/user/bin/env/python3
#-*-conding:utf-8 -*-
# data:202112112
# author:yang
import random
from randomList import randomList
import sort
def divideBlock():
global iList,indexList
sortList = []
for key in indexList:
subList = [i for i in iList if i < key[0]]
key[1] = len(subList)
sortList += subList
iList = list(set(iList) - set(subList))
iList = sortList
print()
return indexList
def blockSearch(iList,key,indexList):
print("iList = %s" %str(iList))
print("indexList = %s" %str(indexList))
print("Find The number : %d" %key)
left = 0
right = 0
for indexInfo in indexList:
left += right
right += indexInfo[1]
if key < indexInfo[0]:
break
for i in range(left,right):
if key == iList[i]:
return i
return -1
if __name__ == "__main__":
indexList = [[250,0],[500,0],[750,0],[1000,0]]
iList = sort.quickSort(randomList(20))
print("iList1:",iList)
divideBlock()
print("iList2:",iList)
keys = [random.choice(iList),random.randrange(min(iList),max(iList))]
for key in keys:
res = blockSearch(iList,key,indexList)
if res >= 0:
print("%d is in the list,index is %d.\n"%(key,res))
else:
print("%d is not in the list.\n"%key)result
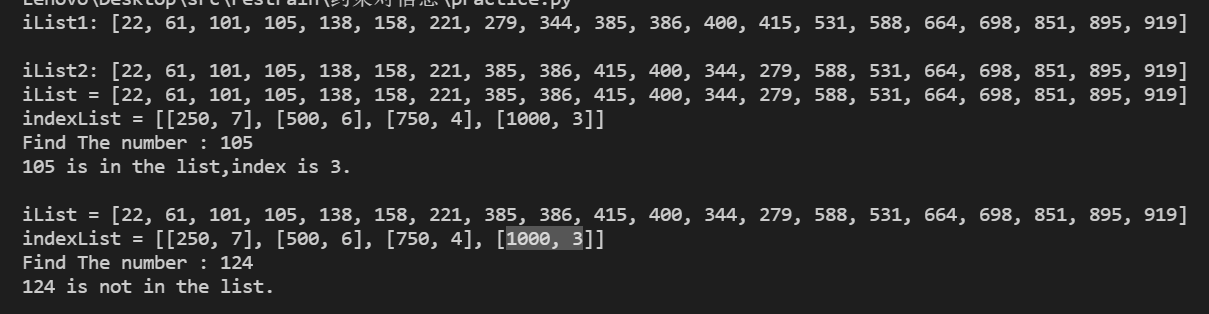Summary
Block search can be regarded as an advanced algorithm of sequential search. Although it will take some time to block, the search will be much faster in the later stage. In general, block search is faster than sequential search.
Reference
Graphical leetcode primary algorithm (python version) -- Hu Songtao