Dynamic diagram display and explanation of eight sorting

Insert sort

Insertion sorting means that in the elements to be sorted, assuming that the first n-1 (where n > = 2) numbers are already in good order, insert the nth number into the previously arranged sequence, and then find the appropriate position so that the sequence of inserting the nth number is also in good order. According to this method, all elements are inserted until the whole sequence is ordered, which is called insertion sorting. Similar to playing cards
1. Thoughts:

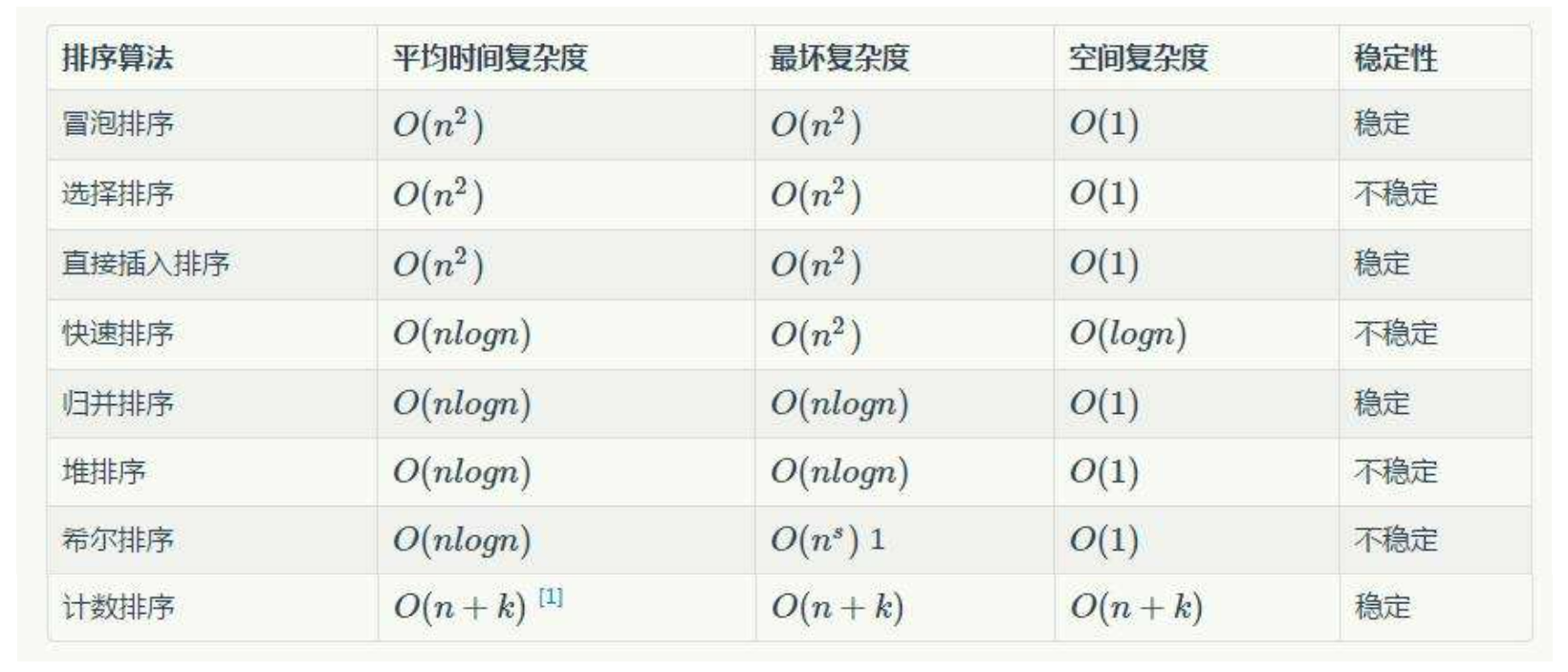
Suppose that a group of numbers has n elements, the first n-1 is ordered, and the position n-1 is end,
Use a temporary variable x to record the value of the nth element. X starts from end, moves forward in turn, moves backward than x, finds a stop smaller than x, and inserts x behind it. Similar to playing cards.

2. Illustration:

Single pass sorting

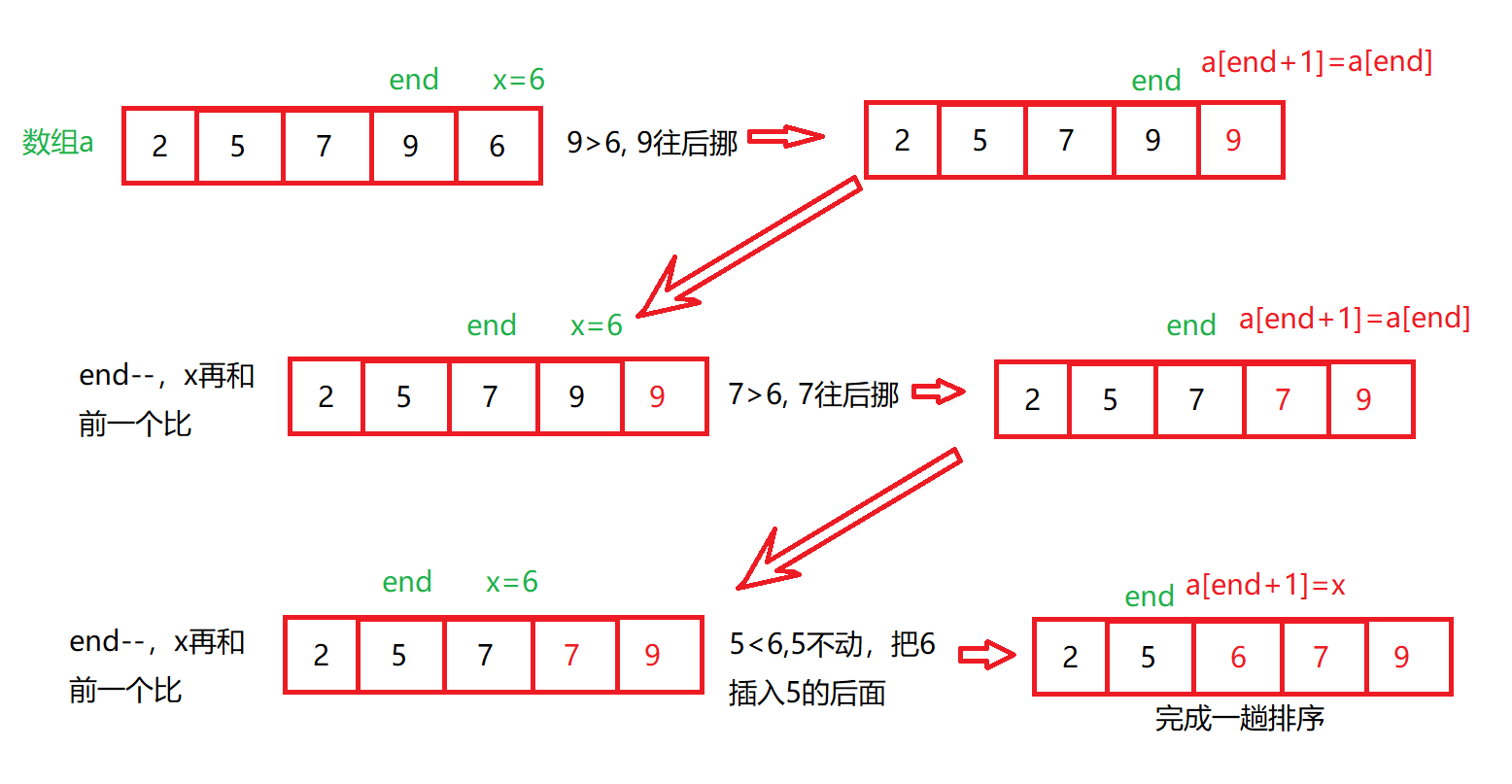
Whole group sorting

Sort the whole group in multiple times according to the single pass sorting method

3. Code implementation

void InsertSort(int*a, int n)
{
	for(int i = 0; i < n-1;i++)
	{
		int end = i;
		int tem = a[end+1];
		while(end > 0)
		{
			if(a[end] > tem)//Bigger than tem move back
			{
				a[end+1] = a[end];
				end--;
			}
			else//Smaller than tem stop
			{
				break;
			}				
		}
		a[end+1] = tem;//Insert tem in the back
	}
}

4. Performance analysis

• Time complexity: O(N^2)
• Space complexity: O(1)
• Stability: stable

Shell Sort

Hill sort is also an insertion sort. It is a more efficient improved version of the direct insertion sort algorithm, also known as "reduced incremental sort". Hill sorting is an unstable sorting algorithm.

1. Thoughts:

Divide an array into gap groups. Gap is also the spacing between two adjacent elements in each group. Direct insertion sort (also known as pre sort) is performed on each group to make the whole array close to order. After the pre sorting is completed, make gap=1, that is, at the end of the whole array, conduct a single pass sorting. The array is ordered and the sorting is completed.
You can perform multiple pre sorting to make the array closer to order (specific method: after completing one pre sorting, change gap to perform pre sorting again)
The smaller the gap, the slower the row, and the closer the array is to order.

2. Illustration

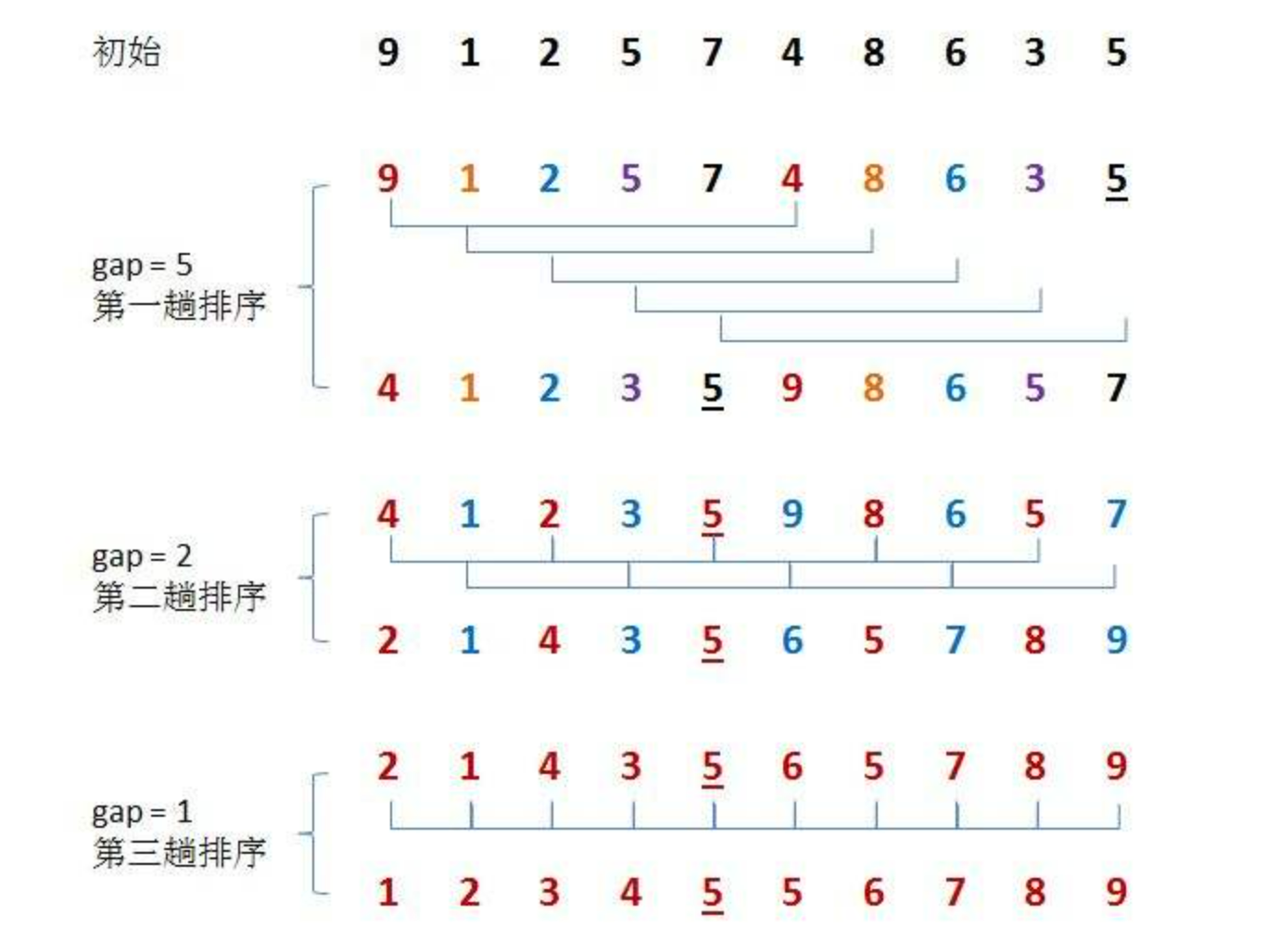
3. Code implementation

void ShellSort(int* a, int n)
{

	for (int gap = n / 2; gap > 0; gap /= 2)//Change gap and perform multiple pre sorting
	{
		for (int i = 0; i < n - gap; i++)//Each time a number is inserted and sorted on its own group,
		//i + + is equivalent to all groups arranged in turn, not one group arranged first and then another group
		{
			int end = i;//This is as like as two peas in the beginning, but the spacing is gap.
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (a[end] > tmp)
				{
					a[end + gap] = a[end];
						end -= gap;
				}
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}

}

4. Performance analysis

• Time complexity: O(N*logN)
• Space complexity: O(1)
• Stability: unstable

Select sort

Selective sorting is a simple and intuitive sorting algorithm. Its working principle is: select the smallest (or largest) element from the data elements to be sorted for the first time, store it at the beginning of the sequence, then find the smallest (large) element from the remaining unordered elements, and then put it at the end of the sorted sequence.

1. Thoughts:

• (find one number at a time) traverse to find the smallest number and put it on the edge

• (find two numbers at a time) traverse the array, find the maximum number and the minimum number, put them on the two sides respectively, and then select the maximum and minimum for the unordered array in the middle, and put them on the two ends of the unordered array in the middle

2. Illustration
Select one number at a time

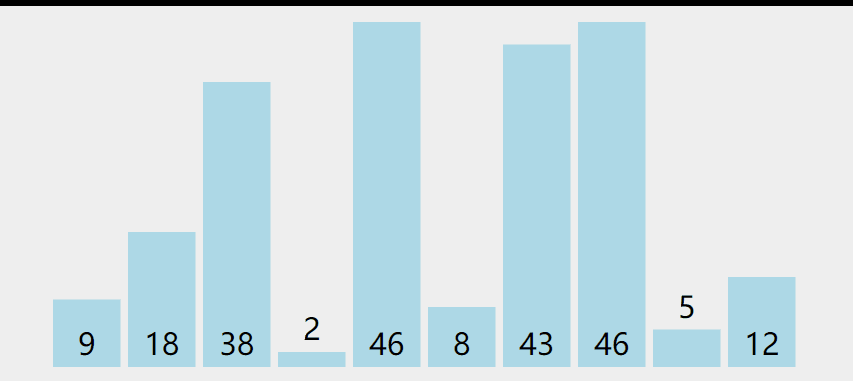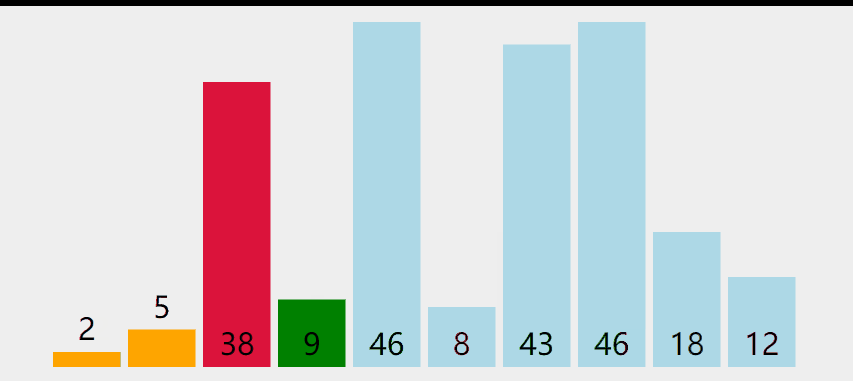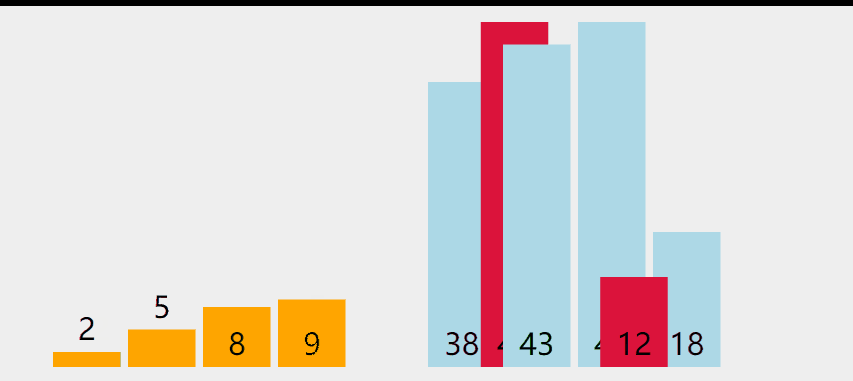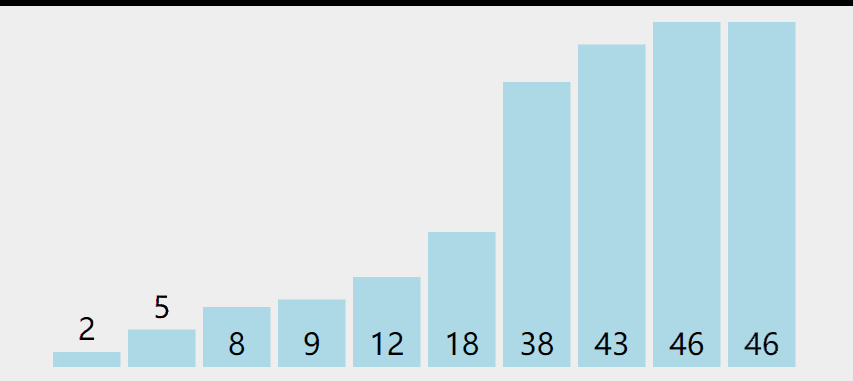
Choose two numbers at a time

Select the small one on the left and the large one on the right. The image should be easy to imagine.

3. Code implementation

void SelectSort(int* a, int n)
{
	int begin = 0; int end = n - 1;
	while (begin < end)
	{
		int min = begin; int max = end;
		for (int i = begin; i <= end; i++)
		{
			if (a[i] < a[min])
				min = i;         //The position subscript of the minimum value in the mini record lookup process
			if (a[i] > a[max])
				max = i;         //maxi the position subscript of the maximum value during record lookup
		}
		
		Swap(&a[min], &a[begin]);  //Put the minimum value found to the left of the array
		if (max = begin)
			min = max;
		Swap(&a[max], &a[end]);     //Put the maximum value found to the far right of the array
	}
	//Control range, and then select and sort the remaining middle numbers
	++begin;
	--end;	
}

Code annotation

The if condition judgment between two Swap functions in the code is a correction to prevent the special case of selecting two numbers at a time. If the position of max is the same as the position of begin, the original value of max position has changed after min and begin are exchanged. If max and end are exchanged without correction, an error will occur.

Swap(&a[min], &a[begin]); 
	if (max = begin)
		min = max;
Swap(&a[max], &a[end]);

Heap sort

1. Thoughts:

You need to use the concept of binary tree size heap. The logical structure of the heap is a complete binary tree, and the physical structure is an array. Give us an array. If we want to arrange it in ascending order, we need to build a lot of arrays; In descending order, build a small pile. Here, we use adjusting AdjustDown() downward to create a large number (the parent node is larger than any child node)

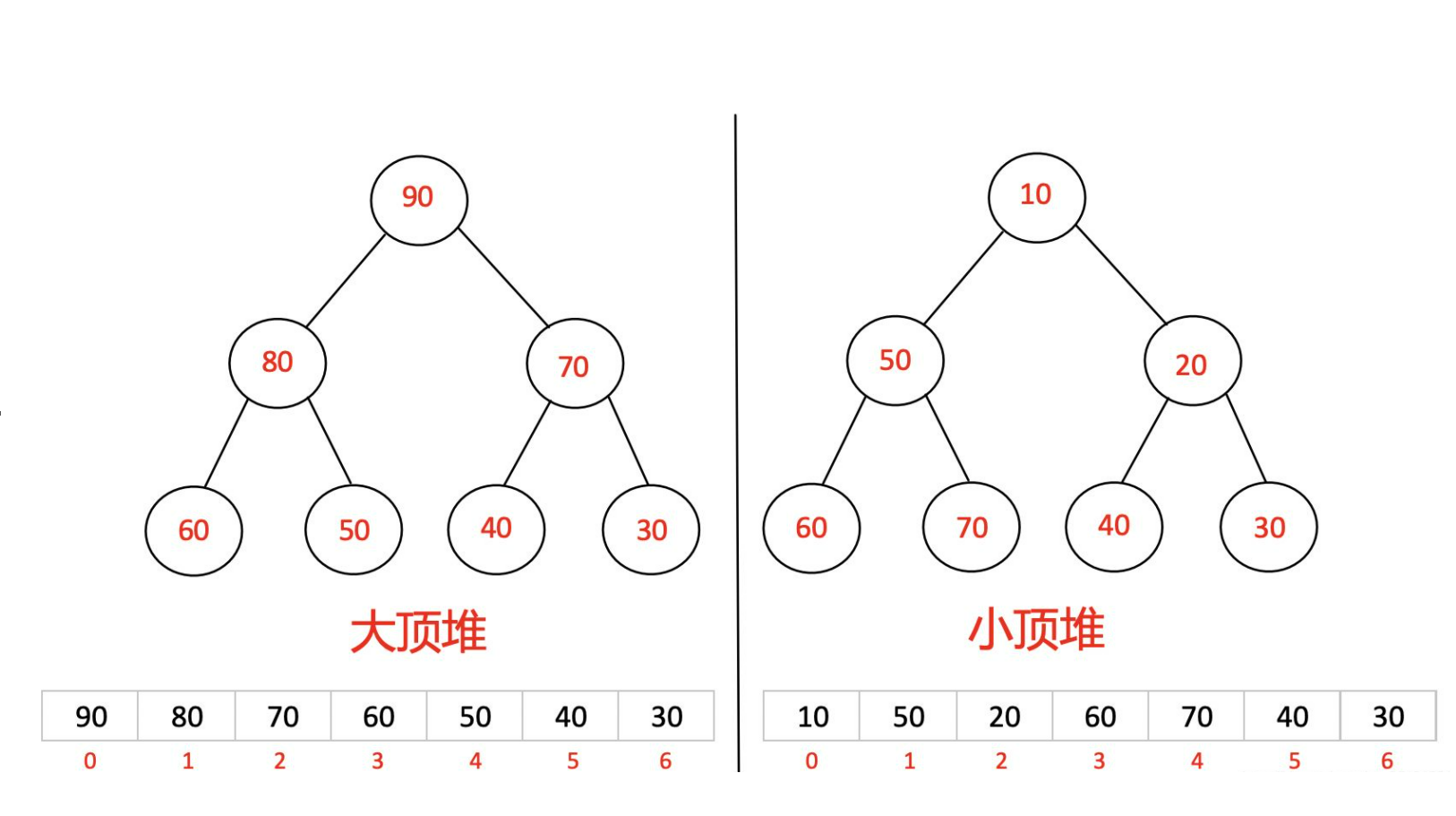
Complete the heap sorting operation diagram of a tree (or subtree)

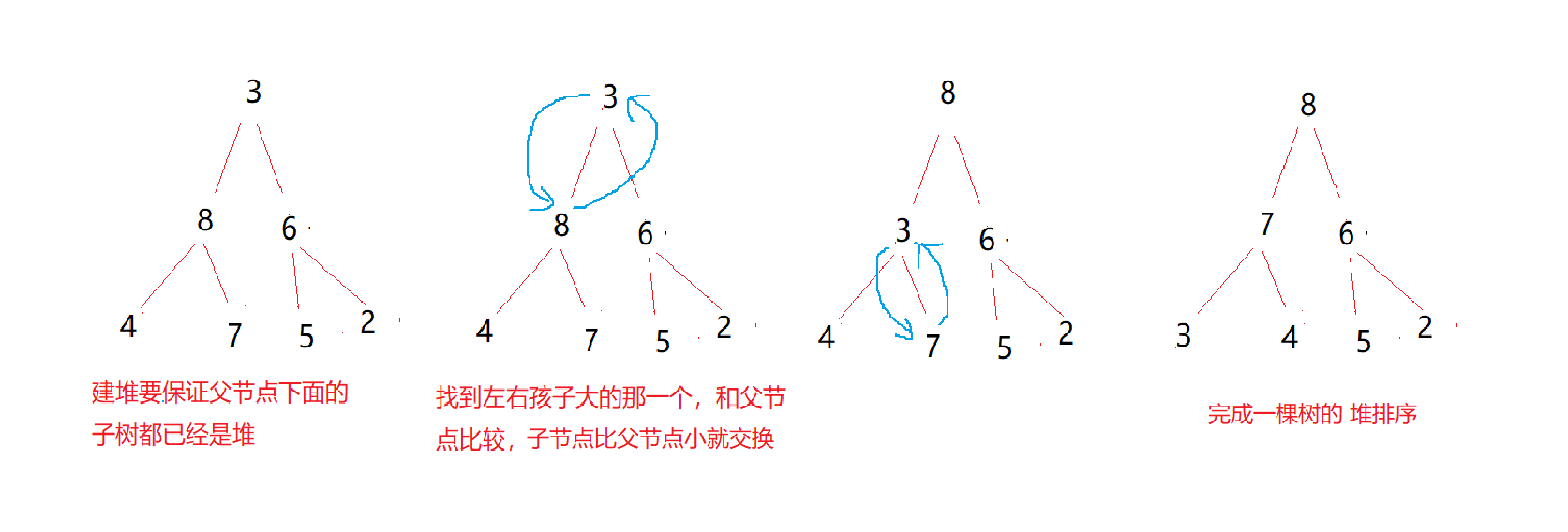
Code implementation of downward adjustment

void Swap(int* x,int* y)//Exchange function
{
	int tem = *x;
	*x = *y;
	*y = tem;
}

void AdjustDown(int*a,int n,int root)
{
	int child = root*2 + 1;
	int parent = root;
	for(child < n)
	{	//Find the older of the two children
		if(a[child+1]<n && a[child+1]>a[child])
			child++;
		if(a[child]>a[parent])
		{
			Swap(&a[child],&a[parent]);
			parent = child;//Compare it down after the exchange
			child = parent*2 - 1;
		}
			

To adjust a tree, you need to make sure that all its subtrees are stacked. Therefore, we can start from the father of the last subtree, adjust a subtree, then adjust from the parent node to the next node, and finally complete the heap sorting of the whole tree.

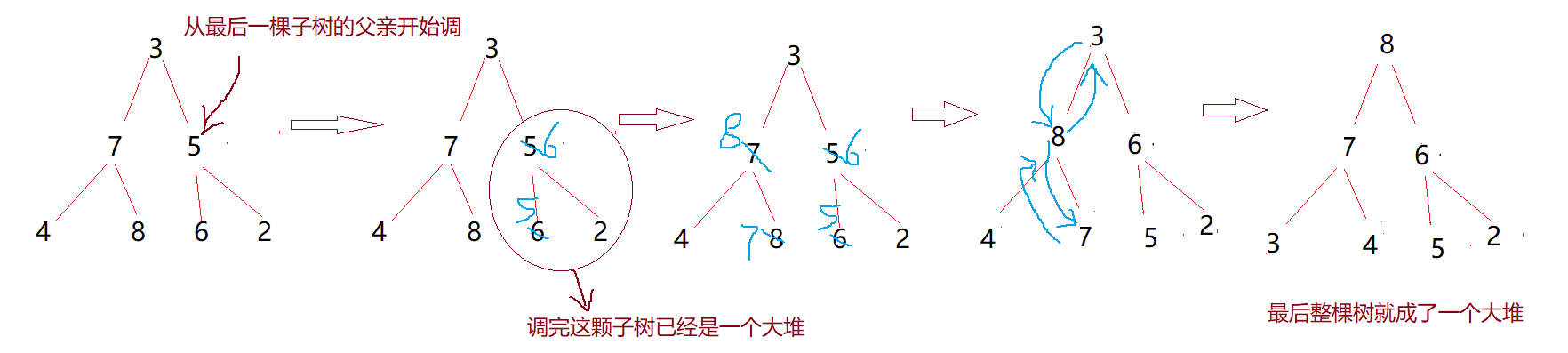
After adjusting the heap, you can sort the data in the heap
Idea: switch the heap top data with the last subtree, and adjust the heap of the first n-1 tree except the tail node

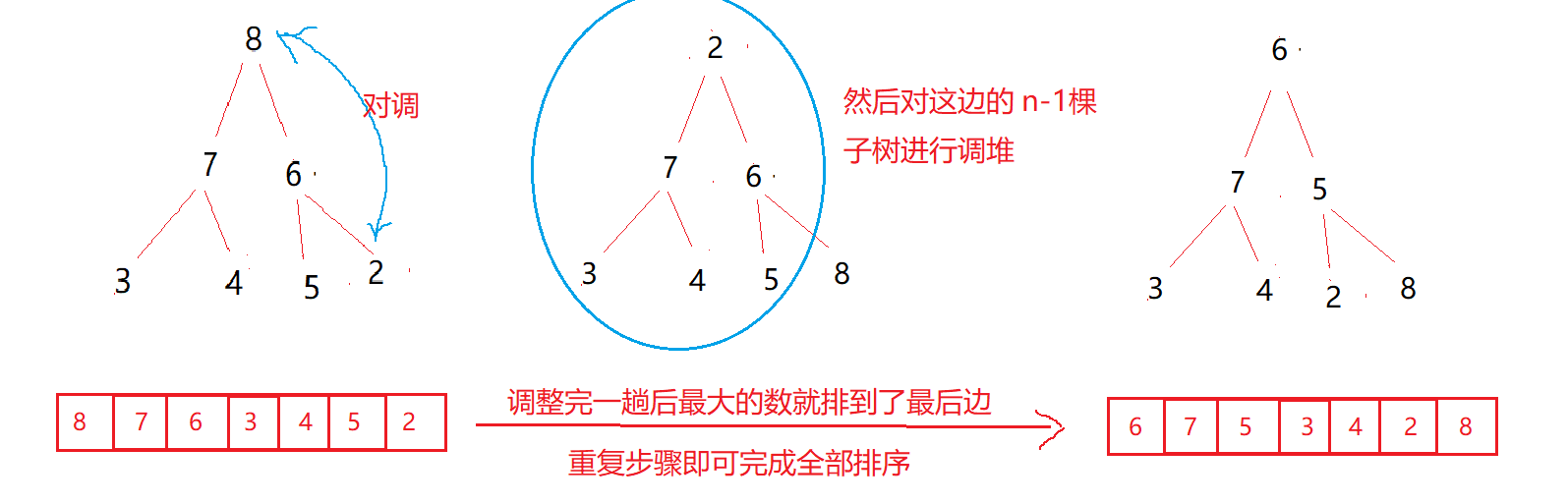
void HeapSort(int* a, int n)//Heap sort
{	//In ascending order, first build the array into a pile
	int parent = (n - 1 - 1) / 2;  //When building a pile, start with the father of the last child
	for (int i = parent; i >= 0; i--)
	{
		AdjustDown(a, n, i);
	}
	for (int end=n-1;end>=0;end--)
	{
		Swap(&a[0], &a[end]);//The top of the pile is exchanged with the last child, and the first n-1 is adjusted into a pile
		AdjustDown(a, end, 0);
	}

}

Bubble sorting

The name of this algorithm comes from the fact that the smaller elements will slowly "float" to the top of the sequence (in ascending or descending order) through exchange, just as the bubbles of carbon dioxide in carbonated drinks will eventually float to the top, so it is called "bubble sorting".

1. Thoughts

Compare two adjacent elements in turn. If the former is larger than the latter, it will be exchanged. Otherwise, continue to compare the next pair (in ascending order), and the largest number will be ranked last after the trip. Then continue sorting the previous numbers to complete the whole group sorting.

2. Illustration

Single pass bubble sort

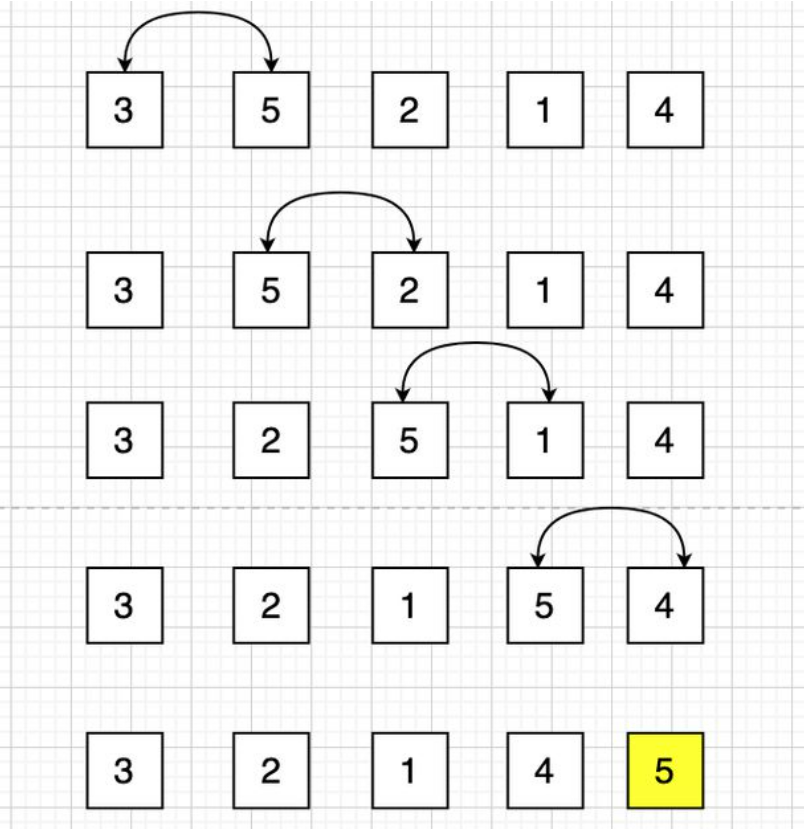
3. Code implementation

void BbubleSort(int* a, int n)
{
	assert(a);
	int end = n;
	while (end > 0)
	{
		int exchange = 0;
		for (int i = 0; i < end - 1; i++)
		{
			if (a[i] > a[i + 1]) //When the judgment condition is if (a [I-1] > a [i]), the loop condition is for (int i = 1; I < end; I + +)
			{
				exchange = 1;//Judge whether the exchange has occurred. If the exchange does not occur in one trip, the array is already in order and does not need to be arranged again
				Swap(&a[i], &a[i + 1]);
			}
		}
		end--;
		if (exchange == 0)//If there is no exchange in one trip, it indicates that the array has order and jumps out of the loop
		{
			break;
		}
	}

Quick sort

Quick sort is an exchange sort method of binary tree structure proposed by Hoare in 1962

1. Thoughts

Here, the quick sort algorithm is used to realize sorting through multiple comparisons and exchanges. The sorting process is as follows:

• Take any element in the element sequence to be sorted as the reference value, and divide the sequence to be sorted into two subsequences according to the sorting code. All elements in the left subsequence are less than the reference value, and all elements in the right subsequence are greater than the reference value. Then repeat the process for the left and right subsequences to divide their subsequences until all elements are arranged in corresponding positions.
• By repeating the above process, we can see that this is a recursive definition, similar to the preorder traversal of binary tree. After the left part is sorted recursively, the right part is sorted recursively. When the sorting of the data in the left and right parts is completed, the sorting of the whole array is completed. The idea of divide and rule is adopted (divide into small areas and make their sections rank respectively)
  

Three digit median method: how to effectively select a benchmark value as a key?

Generally, we choose the leftmost / rightmost or randomly selected value as the key. It is inevitable that the selected value is the maximum or minimum value, so the sorting efficiency will be very low. We can solve this problem by comparing the leftmost / right value with the middle value and taking the middle value as the key.

int MidIndex(int* a,int left, int right)
{
	//int mid = left + right/2;  
	int mid = left + ((right - left) >> 1);//Moving binary one bit to the right is equivalent to dividing two, and moving two bits is equivalent to dividing four
	if (a[left] < a[mid])
	{
		if (a[mid] < a[right])
		{
			return mid;
		}
		else
		{
			return a[left] < a[right] ?  right : left;
		}
	}
	else //(a[left] > a[mid])
	{
		if (a[mid] > a[right])
		{
			return mid;
		}
		else
		{
			return a[right] > a[left] ? left : right;
		}
	}
}

Common methods of dividing reference values into left and right sub intervals

1.Hoare Version (left and right pointer method)

Thought:

Generally, the leftmost / rightmost value is selected as the reference value key,

• The left pointer starts from the beginning, finds a value smaller than the key, and finds the stop;
• Then, the right pointer moves forward from the tail, finds a value greater than key, and finds stop;
• Swap the values of left and right at this time. After the exchange, repeat the steps to continue to find and exchange.
• When left and right finally meet, exchange the value of the meeting position with the key. At this time, the left side of the key is all smaller than the key, and the right side is all larger than the key. Complete interval division

Use principle

(because the last step is to exchange the encounter bit with the key, so as to ensure that the left side of the key is smaller than the key and the right side of the key is larger than the key)

• Select the leftmost one as the reference value, and the right pointer goes first → (go first on the right to find the value less than the key. If you can't find it, go to the left and stop. The left bit is smaller than the key, ensuring that the encounter bit is smaller than the key value)

• Select the rightmost one as the reference value, and the left pointer goes first → (the same principle can ensure that the encounter bit is larger than the key)

code implementation

int partition1(int* a, int left, int right)//Single pass sorting
{
	int mid = MidIndex(a, left, right);//Triple median
	Swap(&a[left], &a[mid]);//Replace the middle digit with left

	int keyi = left;
	while (left < right)
	{
		while (left < right && a[right] >= a[keyi])
			right--;
		while (left < right && a[left] <= a[keyi])
			left++;
		Swap(&a[left], &a[right]);
	}
	Swap(&a[left], &a[keyi]);
	return left;

Special scene

In these two cases, if left and right cannot find the corresponding values, they will go all the way, resulting in crossing the boundary. In order to prevent crossing the boundary, add the judgment condition left < right in the while loop

Recursive program defect: too deep recursion will lead to stack overflow

2. Excavation method

Pit digging method is a deformation of left-right pointer method
Thought:

• Save the first value as the reference value into the temporary variable key to form a pit pivot
• Suppose you choose the left as the pit, then go first on the right, find the small one, put it in the pit, and the right will become a new pit
• Then go left, find the big one, put it in the pit, and the left becomes a new pit. Then go to the right and repeat the steps.
• When meeting and stopping, fill the key value into the pivot pit

graphic

code implementation

int partition2(int* a, int left,int right)
{
	int mid = MidIndex(a, left, right);
	Swap(&a[left], &a[mid]);

	int key = a[left];
	int pivot = left;
	while (left < right)
	{
		while(left<right && a[right] > key)
			right--;
		a[pivot] = a[right];
		pivot = right;

		while (left < right && a[left] < key)
			left++;
		a[pivot] = a[left];
		pivot = left;
	}
	a[pivot] = key;
	return pivot;
}

3. Front and rear pointer method

Thought:

• Initially, the prev pointer points to the beginning of the sequence, the cur pointer points to the next position of prev, and the reference value key is taken
• Cur looks for the small one. After finding the small one, + prev takes a step back and exchanges cur and prev (equivalent to finding the small one and moving forward)
• cur takes the whole sequence and exchanges prev and key.

Illustration:

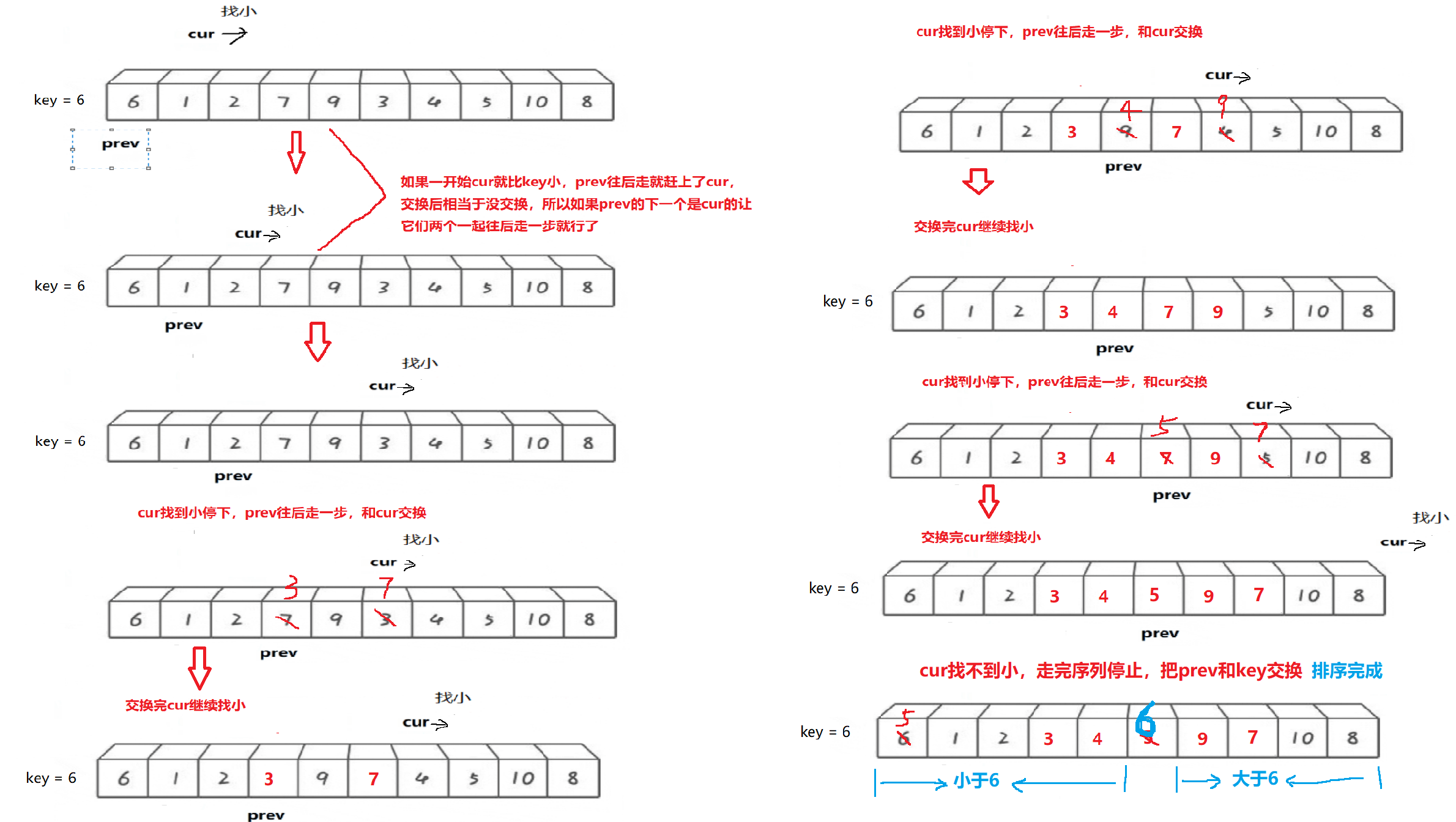
code implementation

int partition3(int* a, int left, int right)
{
	int mid = MidIndex(a, left, right);
	Swap(&a[left], &a[mid]);

	int key = left;
	int prev = left;
	int cur = left + 1;
	while (cur <= right)
	{
		if (a[cur] < a[key] && ++prev != cur)
		{                      //If the cur is smaller than the key at the beginning, the prev will catch up with the cur when it goes back. After the exchange, it is equivalent to no exchange. Therefore, if the next prev is cur, let them go back together
			Swap(&a[cur], &a[prev]);
		}
		cur++;
	}
	Swap(&a[prev], &a[key]);
	return prev;
}

Recursive inter cell optimization

The deeper the recursive call level and the more interval division, the more recursive calls, and the lower the efficiency. We can consider sorting the following layers with other sorting methods, which can greatly reduce the number of calls to recursion, prevent stack overflow and improve sorting efficiency.

Code summary

//Triple median
int MidIndex(int* a,int left, int right)
{
	//int mid = left + right/2;  
	int mid = left + ((right - left) >> 1);//Moving binary one bit to the right is equivalent to dividing two, and moving two bits is equivalent to dividing four
	if (a[left] < a[mid])
	{
		if (a[mid] < a[right])
		{
			return mid;
		}
		else
		{
			return a[left] < a[right] ?  right : left;
		}
	}
	else //(a[left] > a[mid])
	{
		if (a[mid] > a[right])
		{
			return mid;
		}
		else
		{
			return a[right] > a[left] ? left : right;
		}
	}
}

//Interval division 1 Hoare left and right pointers
int partition1(int* a, int left, int right)//Single pass sorting
{
	int mid = MidIndex(a, left, right);//Triple median
	Swap(&a[left], &a[mid]);//Replace the middle digit with left

	int keyi = left;
	while (left < right)
	{
		while (left < right && a[right] >= a[keyi])
			right--;
		while (left < right && a[left] <= a[keyi])
			left++;
		Swap(&a[left], &a[right]);
	}
	Swap(&a[left], &a[keyi]);
	return left;
}



//Interval division 2: excavation method.
// Idea: select left or right as the pit. Here, select left as the pit pivot. Key records the current value. Right go first. Right find a number smaller than key and stop,
//       Fill right in the pit, then right make the pit, left go, find the number greater than key, fill in the pit, left make the pit, right go
int partition2(int* a, int left,int right)
{
	int mid = MidIndex(a, left, right);
	Swap(&a[left], &a[mid]);

	int key = a[left];
	int pivot = left;
	while (left < right)
	{
		while(left<right && a[right] > key)
			right--;
		a[pivot] = a[right];
		pivot = right;

		while (left < right && a[left] < key)
			left++;
		a[pivot] = a[left];
		pivot = left;
	}
	a[pivot] = key;
	return pivot;
}
//Interval division 3: front and rear pointers
int partition3(int* a, int left, int right)
{
	int mid = MidIndex(a, left, right);
	Swap(&a[left], &a[mid]);

	int key = left;
	int prev = left;
	int cur = left + 1;
	while (cur <= right)
	{

		if (a[cur] < a[key] && ++prev != cur)
		{
			Swap(&a[cur], &a[prev]);
		}
		cur++;
	}
	Swap(&a[prev], &a[key]);
	return prev;
}

//Quick row
void QuickSort(int* a, int left, int right)
{
	if (left >= right)
		return;
	
	if ((right - left) + 1 < 10)//Inter cell optimization. When recursing to the last few layers, the number of stack frames called is very large, and the nth layer calls 2 ^ (n-1) times
	{                           //The more recursion to the back, the closer it is to order. Other methods can be considered for sorting in the later layers 
		InsertSort(a + left, right - left + 1);//Using insert sorting is more convenient and adaptable
	}
	else
	{
		int keyi = partition2(a, left, right);

		QuickSort(a, left, keyi - 1);
		QuickSort(a, keyi + 1, right);
	}
	

}

4. Express non recursive writing

When the recursion depth is too deep, non recursion is generally used
Thought:

Fast scheduling non recursion needs to be implemented by stack, which is similar to recursion in idea (queue simulation can also be used, similar to sequence traversal). With the help of a stack array of the same size as the original array, each sub interval is saved instead of the stack frame. A large interval is divided into two intervals, one interval is divided and sorted, and the other interval is placed on the stack first.

• Save the interval range begin and end to be sorted to the stack, take out end and begin, and sort [begin,end] into two intervals [begin, keyi-1], keyi, [keyi+1,end], (the left interval is smaller than Keyi, the right interval is larger than Keyi, and Keyi is equivalent to the data that has been sorted, which exists in the corresponding position of the original array)
• Save the divided interval ranges keyi+1, end,begin and keyi-1 to the stack, and take out the left interval for sorting and division. Repeat steps to finish sorting.

To row the left range first, save the right range first and then the left range, because stack data is the principle of last in first out

code implementation

//Non recursive implementation of quick sort.

void QuickSortNonR(int* a, int left, int right)
{
	ST st;
	StackInit(&st);
	StackPush(&st, left);//Save the range to the stack
	StackPush(&st, right);//Stack is last in first out,

	while (!StackEmpty(&st))
	{
		int end = StackTop(&st);
		StackPop(&st);

		int begin = StackTop(&st);
		StackPop(&st);

		int keyi = partition3(a,begin,end);
//At this time, it can be divided into [begin,kei-1],keyi,[kei+1,end]
//The left interval is smaller than keyi, and the right interval is larger than keyi. keyi is equivalent to the data that has been arranged
		if (keyi + 1 < end)
		{
			StackPush(&st, keyi + 1);
			StackPush(&st, end);
		}
		if (begin < keyi - 1)
		{
			StackPush(&st, begin);
			StackPush(&st, keyi - 1);
		}
	}

	StackDestroy(&st);
}

Illustration:
Advantages of non recursion:

The non recursive stack space is generated by malloc and uses the heap space in the storage space (up to 4G). The essence of recursion is to open up stack frames and use the stack space in the storage space (generally only 4Mb-8Mb). There is no risk of overflow

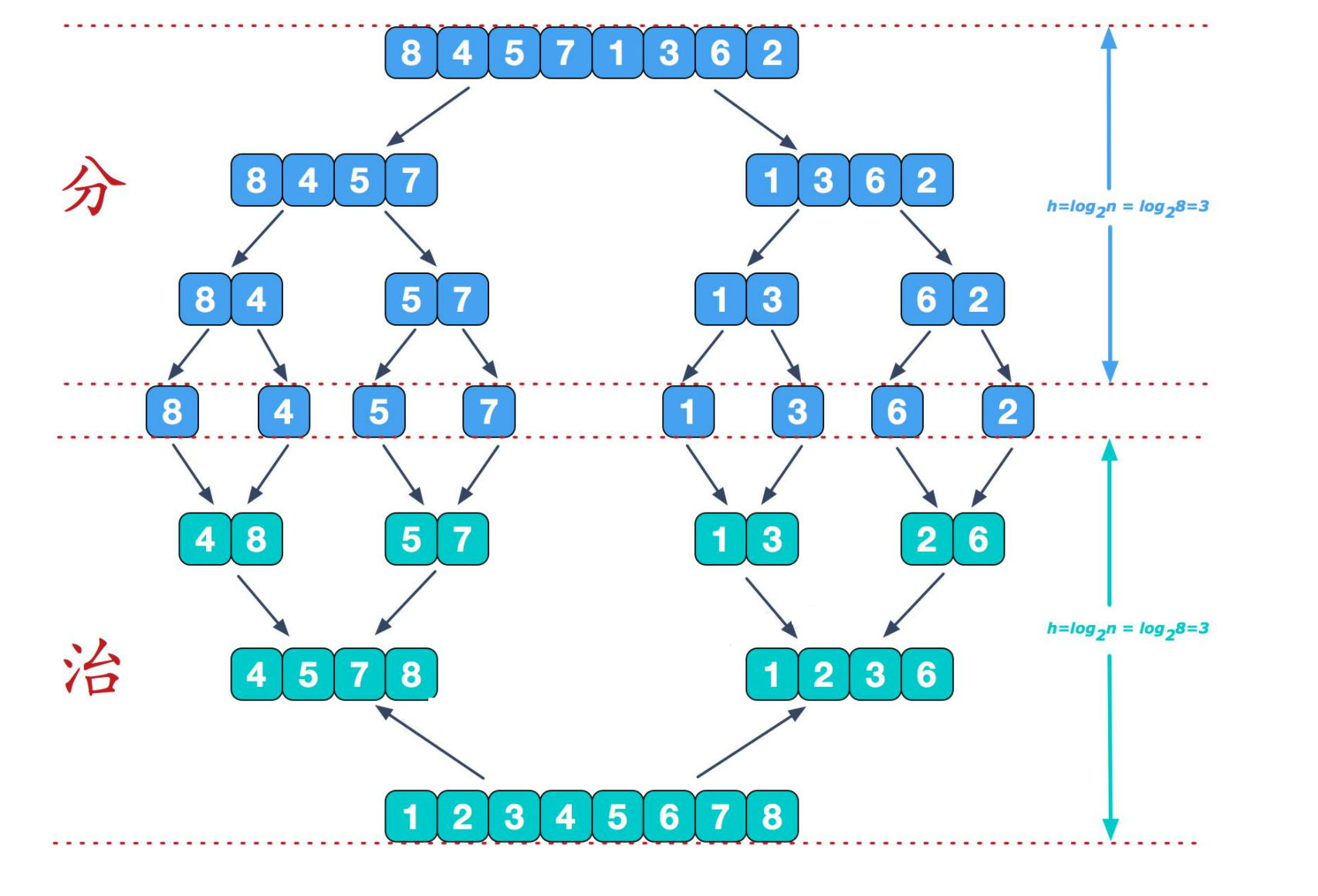
Merge sort

Merge sort is to merge two ordered intervals into an ordered array, which needs to be completed with the help of an additional array space. It is also a model of divide and conquer recursion.

Thought:

• Divide an array into two intervals. If you want the left and right intervals to be orderly, you should continue to divide the left and right intervals until they are not divisible.
• Starting from the minimum interval finally divided, go back to the regression Union, merge every two groups into a group in the additional space, put back the original array after merging, and then merge its right interval. Finally, after the whole merging, put it back into the original array.

Illustration:


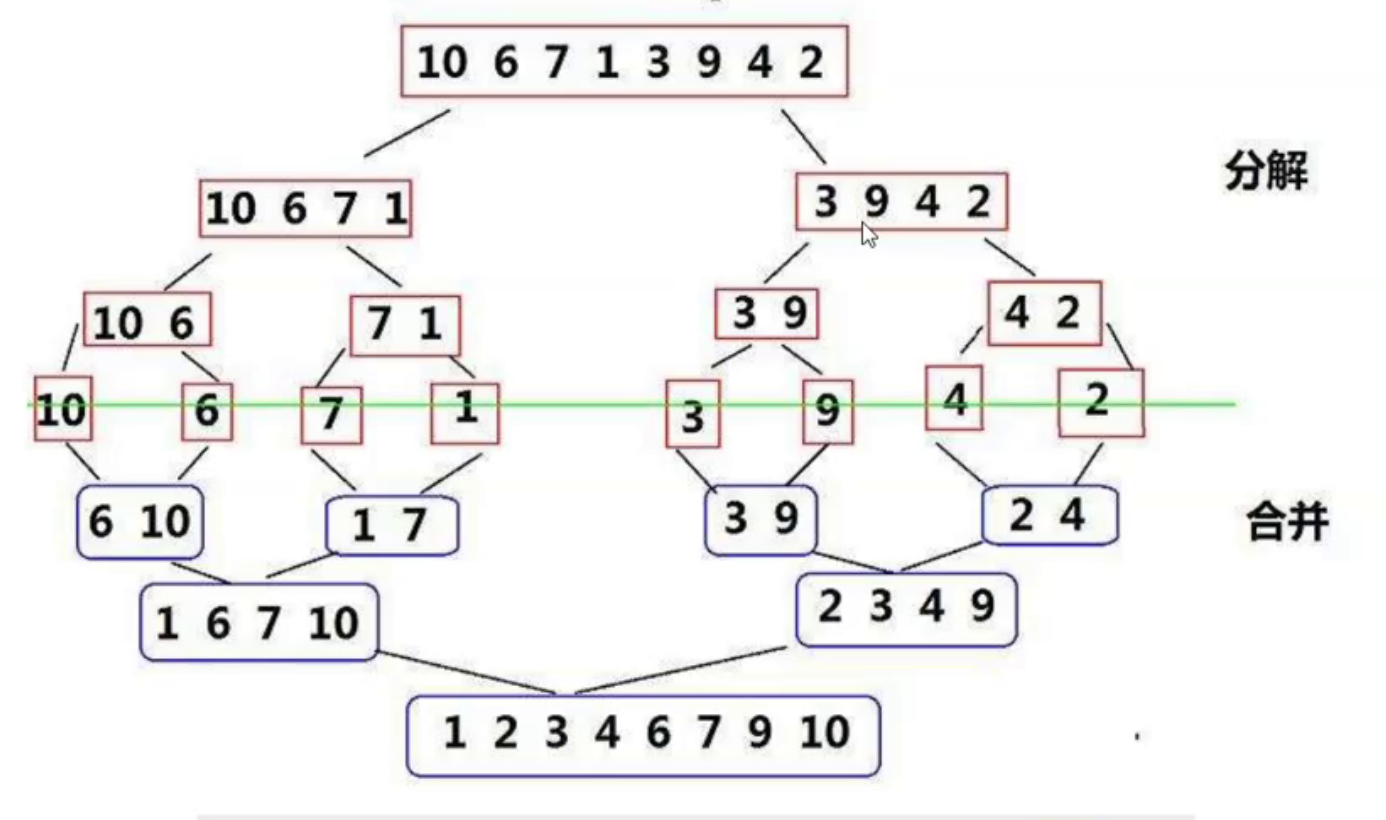
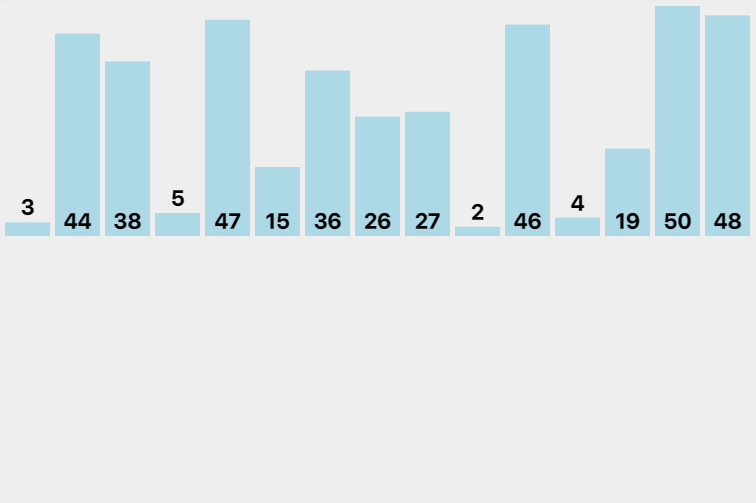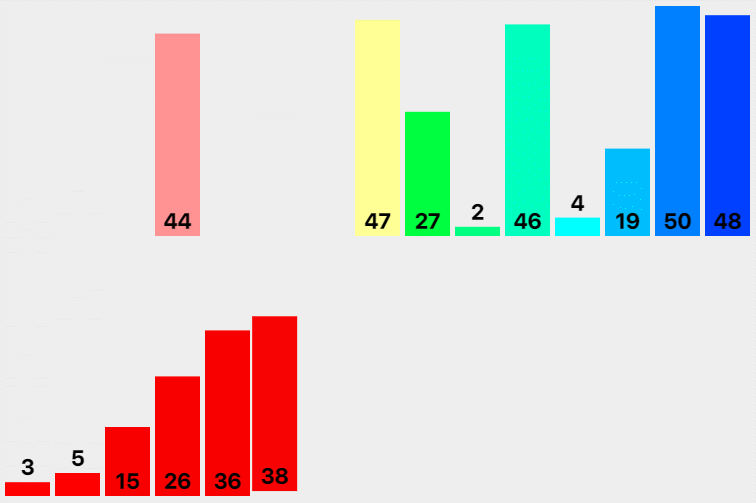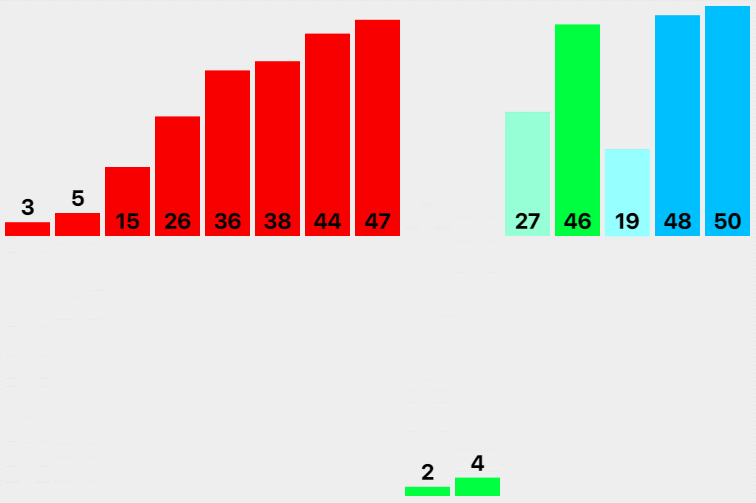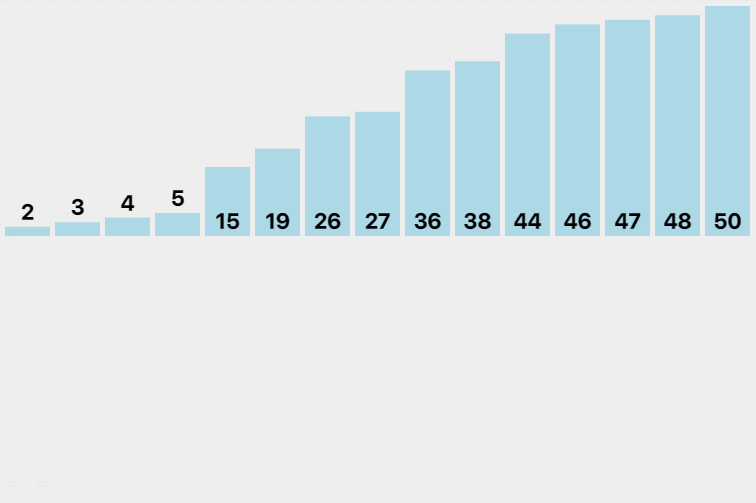
code implementation

//Merge the sub functions of the function to realize the division and sorting of intervals
void _MergeSort(int* a, int left, int right, int* tem)
{
	if (left >= right)
		return;

	int mid = left + (right - left) / 2;
	//[left,mid]  [mid+1,right]
	_MergeSort(a,left,mid,tem);        //Similar to binary tree post order
	_MergeSort(a, mid + 1, right, tem);

	int begin1 = left, end1 = mid;
	int begin2 = mid + 1, end2 = right;
	int i = left;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			tem[i++] = a[begin1++];
		}
		else
		{
			tem[i++] = a[begin2++];
		}
	}
	//One of the two groups must be finished first. Put the unfinished group behind
	while (begin1 <= end1)
	{
		tem[i++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tem[i++] = a[begin2++];
	}
	//Put the merged values in the tmp array back to the original array
	for (int j = left; j <= right; j++)
	{
		a[j] = tem[j];
	}
}
//Merge function
void MergeSort(int* a, int n)
{
	int* tem = (int*)malloc(sizeof(int) * n);//Open up additional array space
	if (tem == NULL)
	{
		printf("malloc failed\n");
		exit(-1);
	}
	_MergeSort(a, 0, n - 1, tem);   //Sorting using sub functions

	free(tem);
	tem = NULL;
}

performance analysis

Time complexity: (N*logN)
Space complexity: O(N)
Stability: stable
Disadvantages: additional space is required

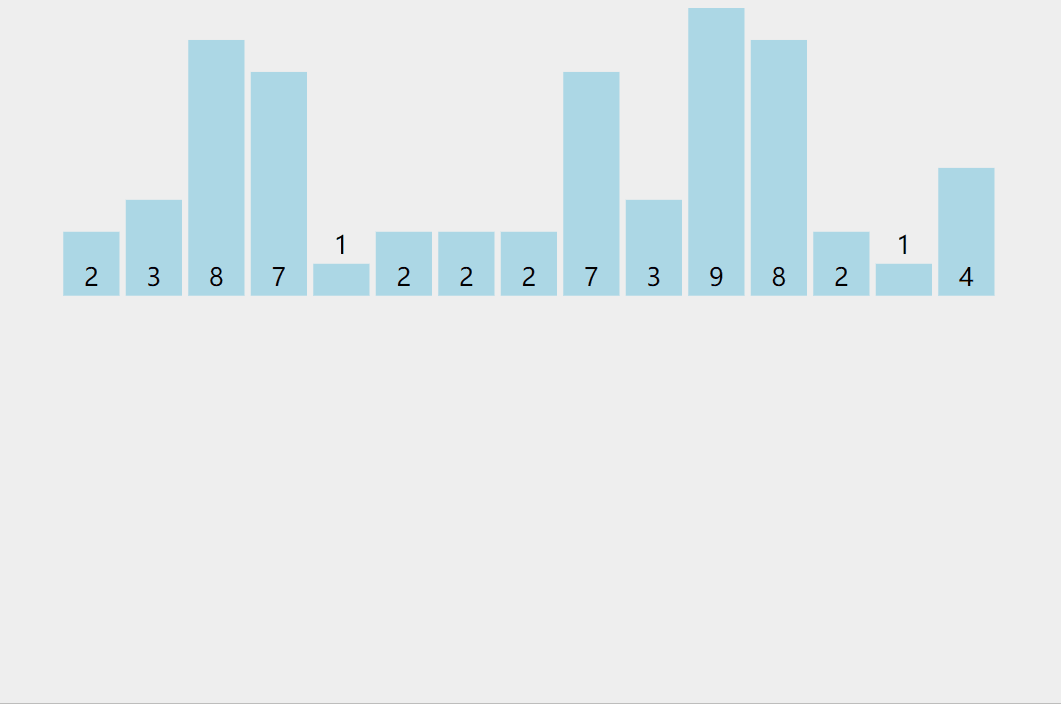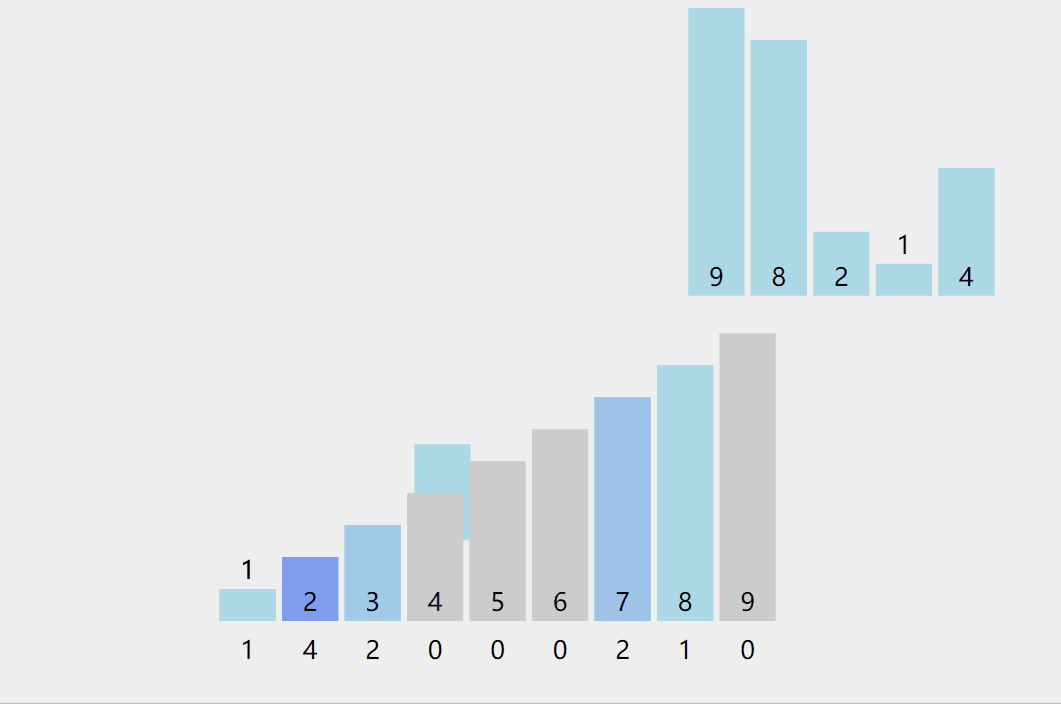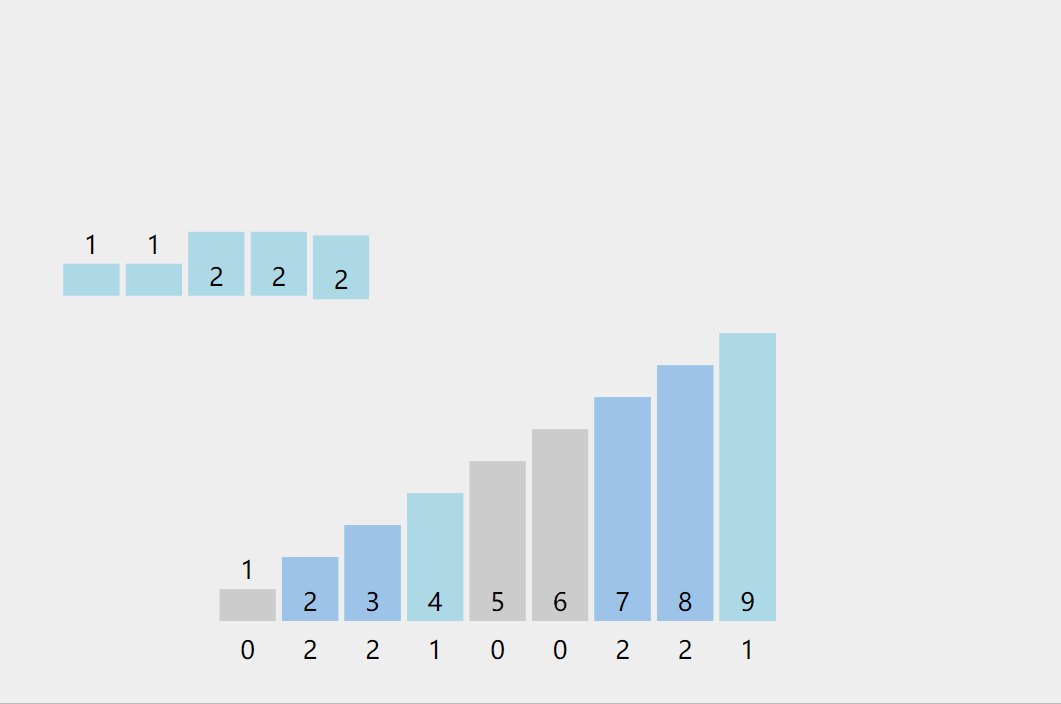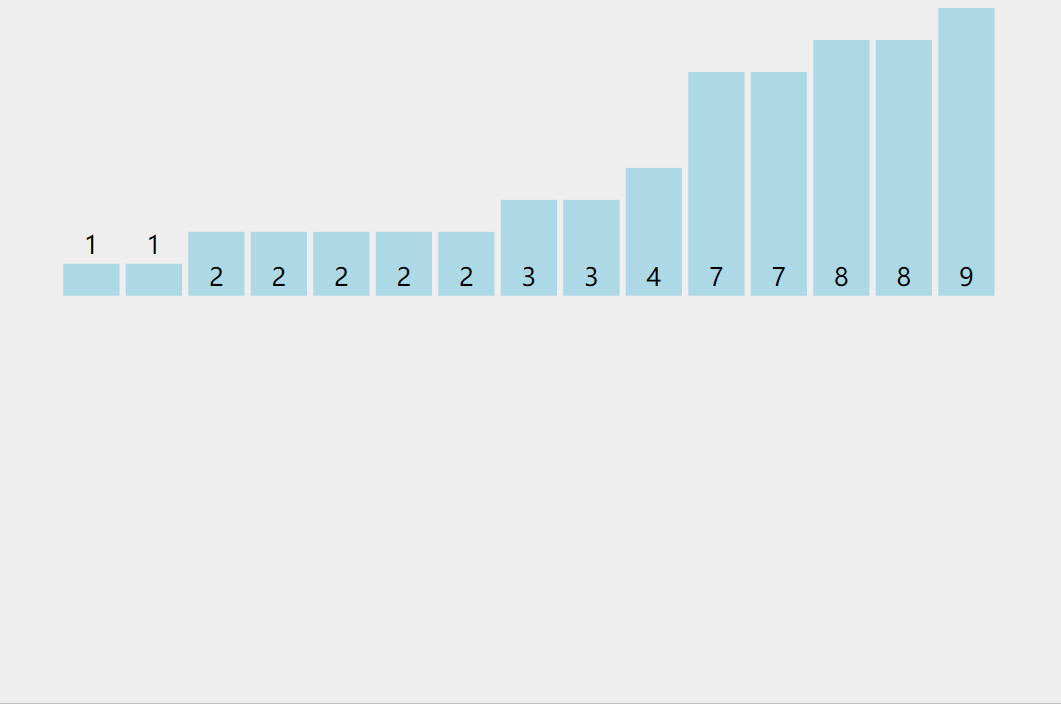
Count sort

Counting sorting is a non comparison based sorting algorithm, which was proposed by Harold H. Seward in 1954. Its advantage is that when sorting integers in a certain range, its complexity is Ο (n+k) (where k is the range of integers), faster than any comparison sorting algorithm. [1] Of course, this is a practice of sacrificing space for time, and when o (k) > O(nlog(n)), its efficiency is not as good as comparison based sorting (the lower limit of time complexity of comparison based sorting is O(nlog(n)) in theory, such as merge sorting and heap sorting

Thought:

• Find the maximum and minimum values in the array to determine the size of the count array to be opened
• All values in the count array are initialized to 0, the original array is traversed, and the count array is used to count the occurrence times of the value of the original array. Once it occurs, the value mapped in the count array is added by one
• Put the relative values of the records in the count array back to the original array in order

Illustration:

code implementation

void Countsort(int* a, int n)
{
	int min = a[0]; int max = a[0];
	for (int i = 0; i < n; i++)
	{
		if (a[i] < min)
			min = a[i];
		if (a[i] > max)
			max = a[i];
	}
	
	int range = max - min + 1;
	int* count = (int*)malloc(sizeof(int) * range);
	memset(count, 0, sizeof(int) * range);
	if (count == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	//Statistical times
	for (int i = 0; i < n; i++)
	{
		count[a[i] - min]++;
	}
	//Sort by number of times
	int j = 0;
	for (int i = 0; i < range; i++)
	{
		while (count[i]--)
		{
			a[j++] = i + min;
		}
	}
}

summary