807. Maintain the urban skyline
2021.12. 13 one question per day
Title Description
Give you a city composed of N x n blocks, each block contains a cube building. Give you an n x n integer matrix grid with subscript starting from 0, where grid[r][c] represents the height of the building located in row r and column c.
The skyline of a city is the external outline of all buildings when the city is viewed from a distance. The skyline observed from the four main directions of East, South, West and North may be different.
We are allowed to increase the height of any number of buildings by any increment (the increment of different buildings may be different). The height of buildings with height of 0 can also be increased. However, the increased height of buildings cannot affect the skyline obtained by observing the city from any main direction.
Return the sum of the maximum height increment that the building can increase without changing the urban skyline observed from any main direction.
Example 1:
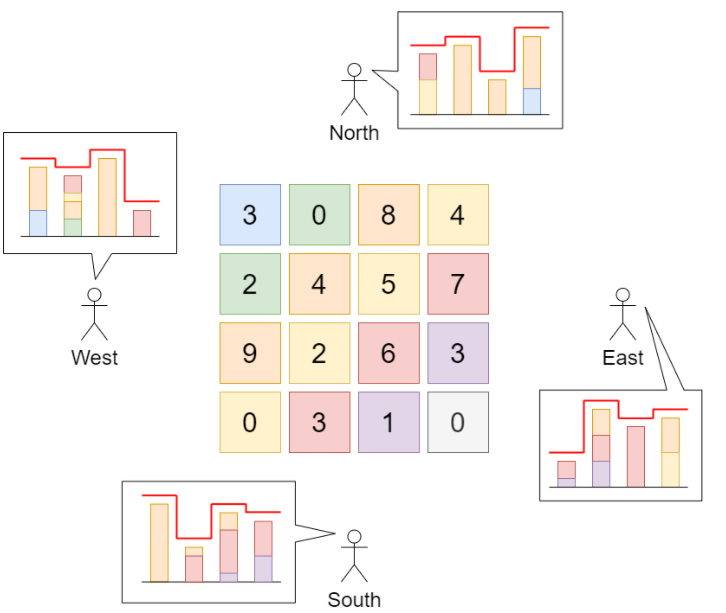
Input: grid = [[3,0,8,4],[2,4,5,7],[9,2,6,3],[0,3,1,0]]
Output: 35
Explanation: the height of the building is shown in the center of the figure above.
Draw the skyline from different directions in red.
Increase the height of the building without affecting the skyline:
gridNew = [ [8, 4, 8, 7],
[7, 4, 7, 7],
[9, 4, 8, 7],
[3, 3, 3, 3] ]
Example 2:
Input: grid = [[0,0,0],[0,0,0],[0,0,0]]
Output: 0
Explanation: increasing the height of any building will change the skyline.
Tips:
n == grid.length
n == grid[r].length
2 <= n <= 50
0 <= grid[r][c] <= 100
Source: LeetCode
Link: https://leetcode-cn.com/problems/max-increase-to-keep-city-skyline
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.
thinking
class Solution {
public int maxIncreaseKeepingSkyline(int[][] grid) {
//The maximum height of each position is the lowest height in both horizontal and vertical directions
//Because that's the skyline
int n = grid.length;
int[] col = new int[n];
int[] row = new int[n];
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
col[i] = Math.max(col[i], grid[i][j]);
row[j] = Math.max(row[j], grid[i][j]);
}
}
int res = 0;
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
int temp = Math.min(col[i], row[j]);
res += temp - grid[i][j];
}
}
return res;
}
}
630. Curriculum III
2021.12. 14 one question per day
Title Description
There are n different online courses, numbered from 1 to n. Give you an array of courses, where courses [i] = [duration, lastDayi] means that the i-th course will last for the duration day and must be completed no later than lastDayi.
Your term begins on day 1. And cannot take two or more courses at the same time.
Returns the maximum number of courses you can take.
Example 1:
Input: courses = [[100, 200], [200, 1300], [1000, 1250], [2000, 3200]]
Output: 3
Explanation:
There are four courses here, but you can take up to three:
First, take the first course, which takes 100 days, complete it on the 100th day, and start the next course on the 101st day.
Second, take the third course, which takes 1000 days, complete it on day 1100, and start the next course on day 1101.
Third, take the second course, which takes 200 days and is completed on day 1300.
Course 4 cannot be taken now because it will be completed on day 3300, which is beyond the closing date.
Example 2:
Input: courses = [[1,2]]
Output: 1
Example 3:
Input: courses = [[3,2],[4,3]]
Output: 0
Tips:
1 <= courses.length <= 10^4
1 <= durationi, lastDayi <= 10^4
Source: LeetCode
Link: https://leetcode-cn.com/problems/course-schedule-iii
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.
thinking
class Solution {
public int scheduleCourse(int[][] courses) {
//The range is 4 times of 10, which should be a topological sort, I think
//Is it sorted by due date or by time spent
//If you sort by deadline, you can get the earliest deadline each time, but not the shortest time. Is there a problem
//There should be problems. For example, a few short-term projects can't be completed
//First, clarify the first point. If there is a deadline D1 < = D2 for two courses, it is better to complete course 1 and then course 2 first than vice versa
//This is inevitable, because think about it, if you can learn the back first and then the front, you can certainly learn the front first and then the back, and the reverse is not necessarily the case
//Therefore, all courses are sorted according to the deadline, and the courses are selected in turn
//If an optimal course sequence is currently selected, K1, K2 Kn, judge whether this sequence can be added to the next course
//If the course meets the deadline, you can join, and because the previous sequence is optimal, joining is also optimal
//If the course does not meet the deadline, it depends on whether the course can replace the original sequence of courses
//If the course time in the original sequence is shorter than this course, it cannot be replaced; If one is longer than this, it can be replaced
int n = courses.length;
//Sort by deadline
Arrays.sort(courses, (a, b) -> (a[1] - b[1]));
//Use a priority queue to record the time required for courses in the current sequence and replace the courses at the top of the heap
PriorityQueue<Integer> pq = new PriorityQueue<>((a, b) -> (b - a));
int time = 0;
for(int i = 0; i < n; i++){
int temptime = time + courses[i][0];
//If you can join, insert the last
if(temptime <= courses[i][1]){
pq.offer(courses[i][0]);
time = temptime;
}else{
//If not, replace
if(!pq.isEmpty() && pq.peek() > courses[i][0]){
int t = pq.poll();
pq.offer(courses[i][0]);
time = time - t + courses[i][0];
}
}
}
return pq.size();
}
}
851. Noisy and rich
2021.12. 15 one question per day
Title Description
There are a group of n people as experimental subjects, numbered from 0 to n - 1, in which each person has different amounts of money and different degrees of quiet. For convenience, we call the person numbered X "person x" for short.
Give you an array richer, where richer[i] = [ai, bi] means that person ai has more money than person bi. Give you another integer array quiet, where quiet[i] is the quiet value of person i. The data logic given in richer is self consistent (that is, while person x is richer than person y, there will be no case where person y is richer than person x).
Now, return an integer array answer as the answer, where answer[x] = y on the premise that person y is the quietest person (that is, the person with the smallest quiet value quiet[y]) among all people who must have no less than person x.
Example 1:
Input: richer = [[1,0],[2,1],[3,1],[3,7],[4,3],[5,3],[6,3]], quiet = [3,2,5,4,6,1,7,0]
Output: [5,5,2,5,4,5,6,7]
Explanation:
answer[0] = 5,
person 5 has more money than person 3, person 3 has more money than person 1, and person 1 has more money than person 0.
The only quiet person (with a low quiet value quiet[x]) is person 7,
But it is not clear whether he is richer than person 0.
answer[7] = 7,
Of all people who must have no less than person 7 (this may include person 3, 4, 5, 6 and 7),
The quietest person (with a lower quiet value quiet[x]) is person 7.
Other answers can be explained by similar reasoning.
Example 2:
Input: richer = [], quiet = [0]
Output: [0]
Tips:
n == quiet.length
1 <= n <= 500
0 <= quiet[i] < n
All values of quiet are different from each other
0 <= richer.length <= n * (n - 1) / 2
0 <= ai, bi < n
ai != bi
All number pairs in richer are different from each other
The observation of richer is logically consistent
Source: LeetCode
Link: https://leetcode-cn.com/problems/loud-and-rich
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.
thinking
Writing in this way even timed out, which is equivalent to a topology sort
Because when calculating everyone, we have to traverse the graph once. In fact, we have done a lot of useless work. It should be in a traverse. If we encounter something that can be calculated, we can directly calculate the result. Later, we don't have to traverse this value again
This should be much faster. Think about how to write it
class Solution {
public int[] loudAndRich(int[][] richer, int[] quiet) {
//Two comparative dimensions, one is rich and the other is quiet
//You need to sort the two dimensions first. For the quiet value, for example, check the person with the smallest quiet value in a group of people,
//First, you have to find this group of people, and then directly compare the quiet value of this group of people in the quiet array
//So how to find this group of people is to build a graph according to the relationship given by richer, and then find the answer according to the relationship of this graph
//How to construct this picture is more convenient, because it is unidirectional, so you can build a two-dimensional array
//g[i][j] is true, which means I has more money than j, or directly traverse the richer array
//For example, judge the position of 0, then
int n = quiet.length;
int l = richer.length;
//Count people who are richer than you
Map<Integer, List<Integer>> map = new HashMap<>();
for(int i = 0; i < l; i++){
int rich = richer[i][0];
int poor = richer[i][1];
List<Integer> list = map.getOrDefault(poor, new ArrayList<>());
list.add(rich);
map.put(poor, list);
}
int[] res = new int[n];
for(int i = 0; i < n; i++){
//If there is no relationship with this person
if(!map.containsKey(i)){
res[i] = i;
continue;
}
List<Integer> list = map.get(i);
Queue<Integer> queue = new LinkedList<>();
for(int p : list){
queue.add(p);
}
int min = quiet[i]; //Minimum quiet value
int minp = i;
while(!queue.isEmpty()){
//Current person
int p = queue.poll();
//If the quiet value of the person richer than the current person is less than the quiet value of the current person, replace
if(quiet[p] < min){
min = quiet[p];
minp = p;
}
List<Integer> temp = map.getOrDefault(p, new ArrayList<>());
for(int peo : temp){
queue.add(peo);
}
}
res[i] = minp;
}
return res;
}
}
Change to recursive form, do a processing, too
class Solution {
Map<Integer, List<Integer>> map;
int[] quiet;
int[] res;
public int[] loudAndRich(int[][] richer, int[] quiet) {
//Two comparative dimensions, one is rich and the other is quiet
//You need to sort the two dimensions first. For the quiet value, for example, check the person with the smallest quiet value in a group of people,
//First, you have to find this group of people, and then directly compare the quiet value of this group of people in the quiet array
//So how to find this group of people is to build a graph according to the relationship given by richer, and then find the answer according to the relationship of this graph
//How to construct this picture is more convenient. Because it is unidirectional, you can build a two-dimensional array
//g[i][j] is true, which means I has more money than j, or directly traverse the richer array
//For example, judge the position of 0, then
this.quiet = quiet;
int n = quiet.length;
int l = richer.length;
//Count people who are richer than you
map = new HashMap<>();
for(int i = 0; i < l; i++){
int rich = richer[i][0];
int poor = richer[i][1];
List<Integer> list = map.getOrDefault(poor, new ArrayList<>());
list.add(rich);
map.put(poor, list);
}
res = new int[n];
Arrays.fill(res, -1);
for(int i = 0; i < n; i++){
if(res[i] == -1)
backtracking(i);
}
return res;
}
public int backtracking(int i){
//If there is no relationship with this person
if(!map.containsKey(i)){
res[i] = i;
return i;
}
int min = quiet[i];
int minp = i;
List<Integer> list = map.get(i);
for(int p : list){
//If this person has got the result
int temp = -1;
if(res[p] != -1){
temp = res[p];
//Otherwise recursive
}else
temp = backtracking(p);
if(quiet[temp] < min){
min = quiet[temp];
minp = temp;
}
}
res[i] = minp;
return minp;
}
}
In turn, the graph can be traversed at one time by topological sorting
class Solution {
public int[] loudAndRich(int[][] richer, int[] quiet) {
//Write a topological sort once
int n = quiet.length;
int l = richer.length;
boolean[][] g = new boolean[n][n]; //Wealth points to poverty
int[] inDeg = new int[n]; //Penetration
for(int i = 0; i < l; i++){
g[richer[i][0]][richer[i][1]] = true;
inDeg[richer[i][1]]++;
}
Queue<Integer> queue = new LinkedList<>();
int[] res = new int[n];
for(int i = 0; i < n; i++){
res[i] = i;
if(inDeg[i] == 0)
queue.add(i);
}
while(!queue.isEmpty()){
int top = queue.poll();
//Traverse all those who are poorer than it
for(int i = 0; i < n; i++){
if(g[top][i]){
//If the current rich person's quiet value is less than the poor person's quiet value, then change
if(quiet[res[top]] < quiet[res[i]])
res[i] = res[top];
//This man's penetration is reduced by 1
inDeg[i]--;
if(inDeg[i] == 0)
queue.add(i);
}
}
}
return res;
}
}