Time complexity and space complexity of the algorithm:
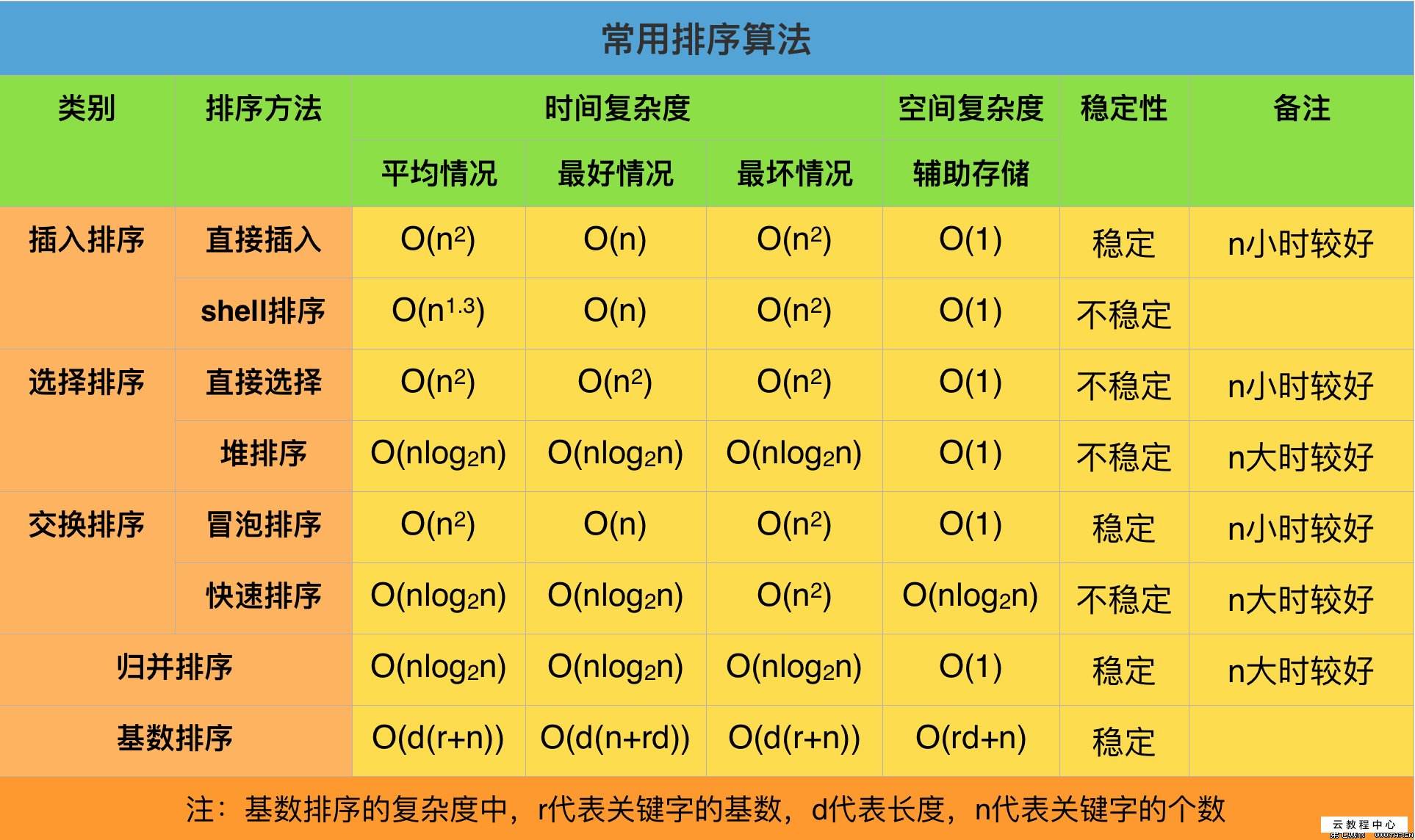
2, Seven sorting algorithms
(1) Bubble sorting
1. Basic thought
Compare the two adjacent numbers in turn, and put the smaller number in the front and the larger number in the back.
2. Dynamic rendering
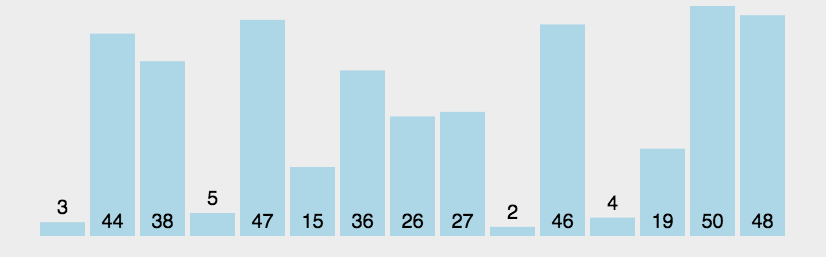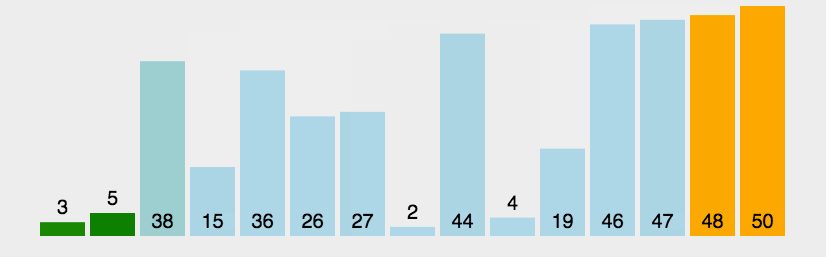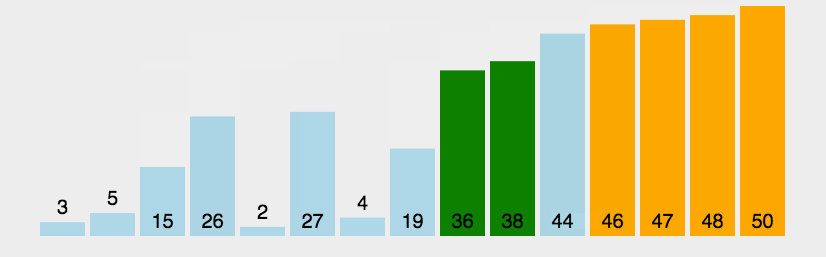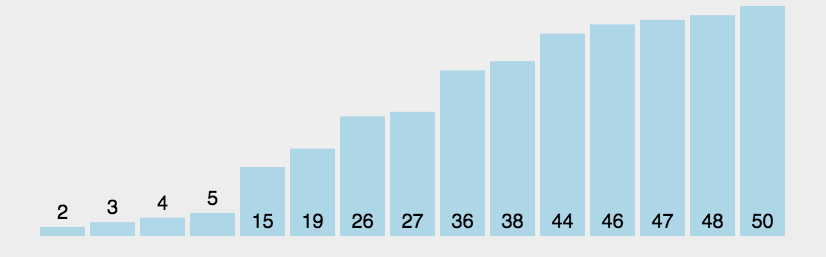
3. Code implementation
//Bubble sorting
private static void bubbleSort(int[] arr){
// Identification variable, indicating whether exchange has been performed
boolean flag = false;
int temp = 0;
for (int i = 0; i < arr.length-1; i++) {
for (int j = 0; j < arr.length-1-i; j++) {
// If the preceding number is larger than the following number, swap
if(arr[j]>arr[j+1]){
flag = true;
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
// In one sort, no exchange has occurred
if(!flag){
break;
}
}
}
4. Speed test
Bubble sort: 120000 data, 23 seconds
(2) Select sort
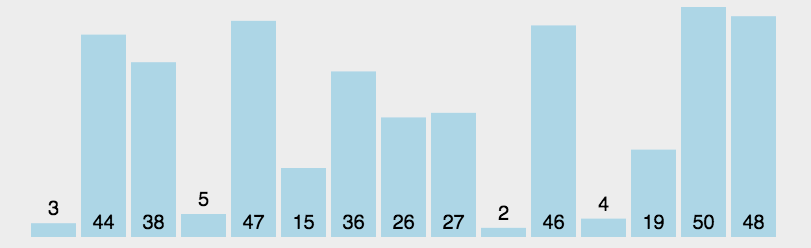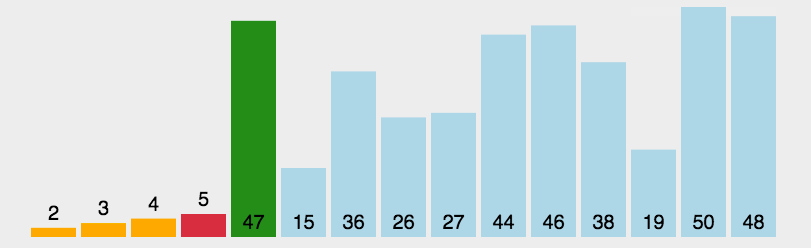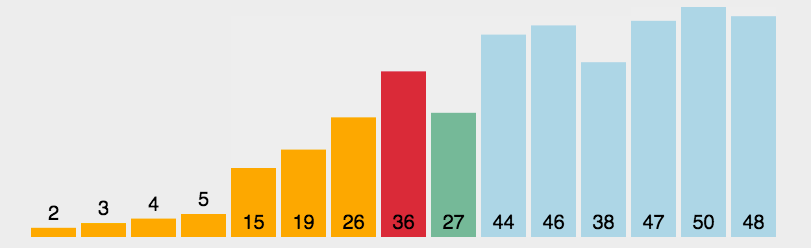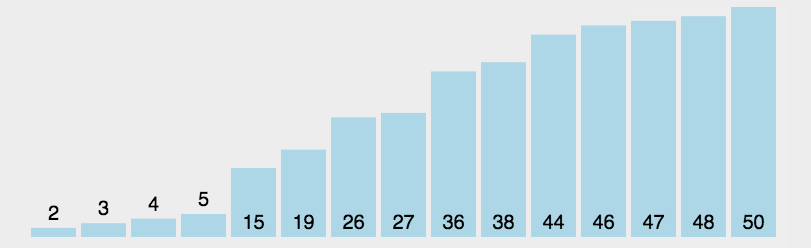
1. Basic thought
(1) Find the smallest element in the sequence and put it in the first position;
(2) Continue to find the smallest element from the remaining unordered elements and put it in the second position;
And so on until sorting is completed.
2. Dynamic rendering
3. Code implementation
//Select sort
public static void selectSort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
int minIndex = i;
int min = arr[minIndex];
for(int j = 1 + i;j<arr.length;j++){
if(min > arr[j]){
min = arr[j];
minIndex = j;
}
}
arr[minIndex] = arr[i];
arr[i] = min;
}
}
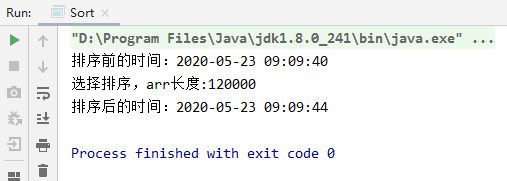
4. Speed test
Select sort: 120000 data, 4 seconds
(3) Insert sort
1. Basic thought
Take the first place of n elements to be sorted as an ordered table and the others as an unordered table. In the sorting process, take a number from the unordered table each time, compare it with the number in the ordered table in turn, and insert it into the appropriate position.
2. Dynamic rendering
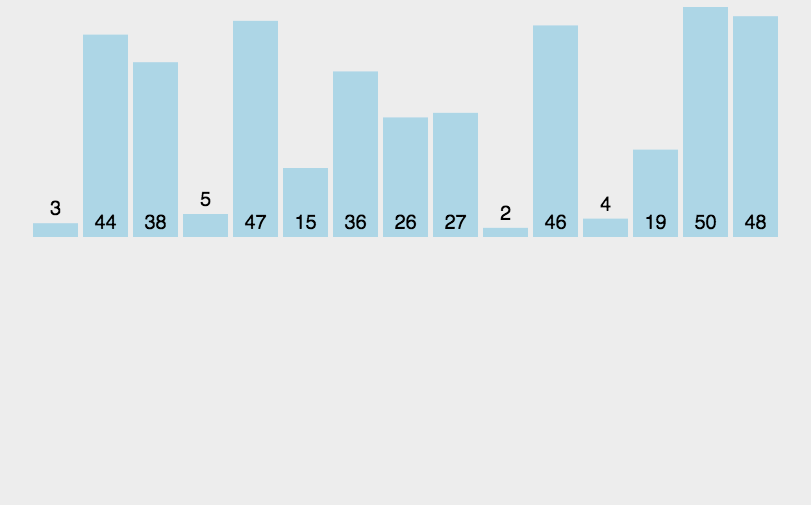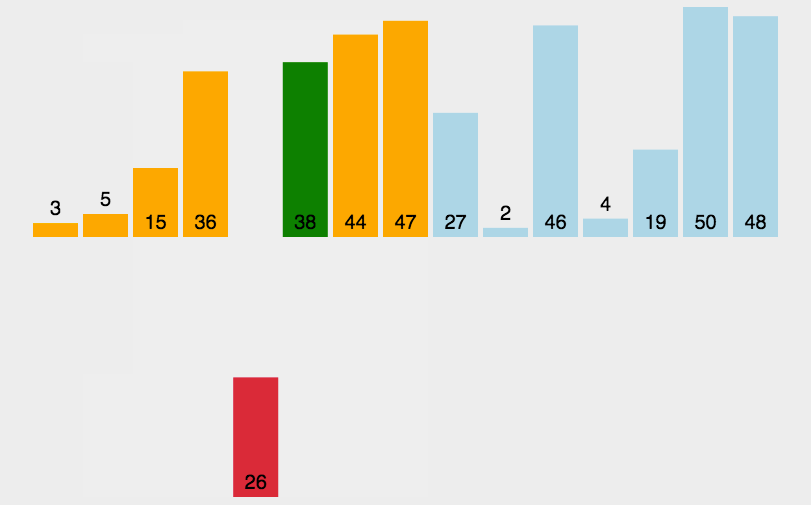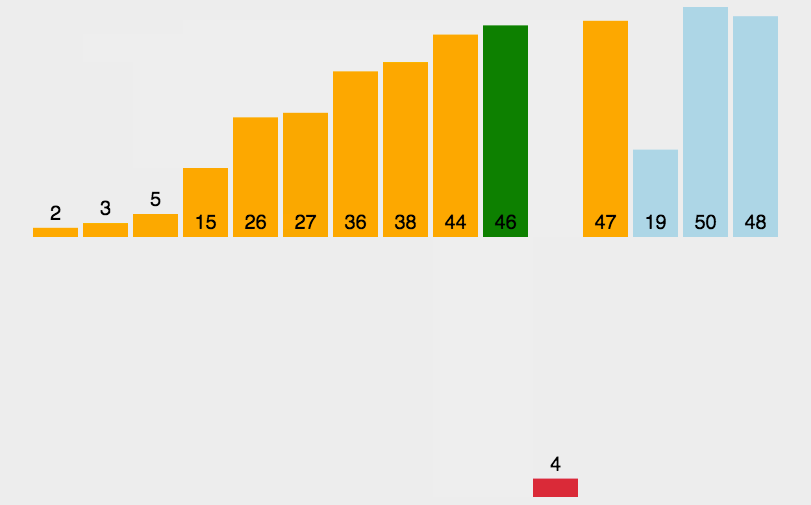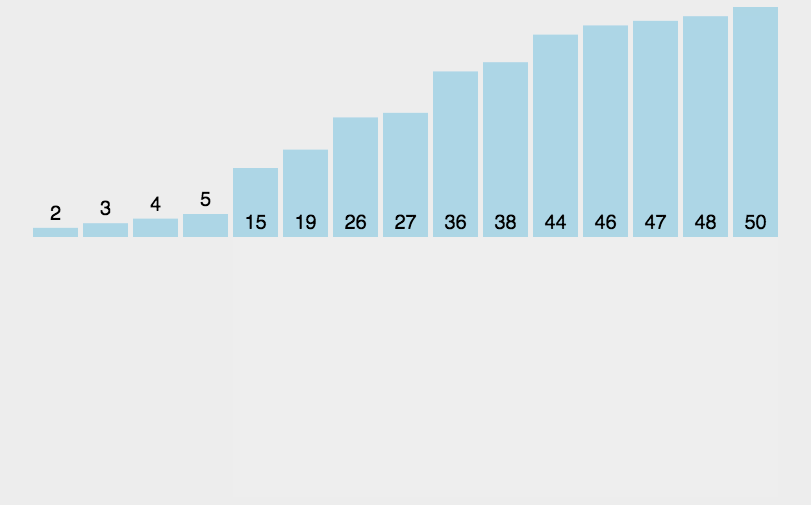
3. Code implementation
//Insert sort
public static void insertSort(int[] arr ){
int insertVal = 0;
int insertIndex = 0;
for (int i = 1; i < arr.length; i++) {
//Defines the number of to insert
insertVal = arr[i];
// That is, the subscript of the number before arr[i]
insertIndex = i - 1;
// Find the insertion position for insertVal
// explain
// 1. Insertindex > = 0 ensure that the insertion position of insertVal is not exceeded
// 2. Insertval < arr [insertindex] the number to be inserted, and the insertion position has not been found
// 3. You need to move arr[insertIndex] backward
while(insertIndex >= 0 && insertVal < arr[insertIndex]){
arr[insertIndex+1] = arr[insertIndex];
insertIndex--;
}
// When exiting the while loop, the insertion position is found, insertIndex + 1
if(insertIndex + 1 != i){
arr[insertIndex+1] = insertVal;
}
}
}
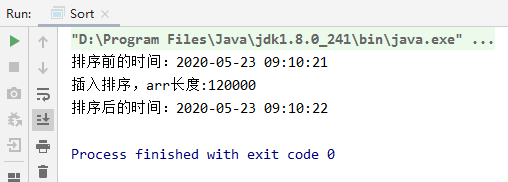
4. Speed test
Insert sort: 120000 data, 1 second
(4) Hill sort
1. Basic thought
Hill sort is also an insertion sort. It is a more efficient version of simple insertion sort after improvement, also known as reduced incremental sort. At the same time, the algorithm also breaks through O(n) ²) One of the first algorithms. It differs from insert sorting in that it preferentially compares distant elements.
2. Renderings
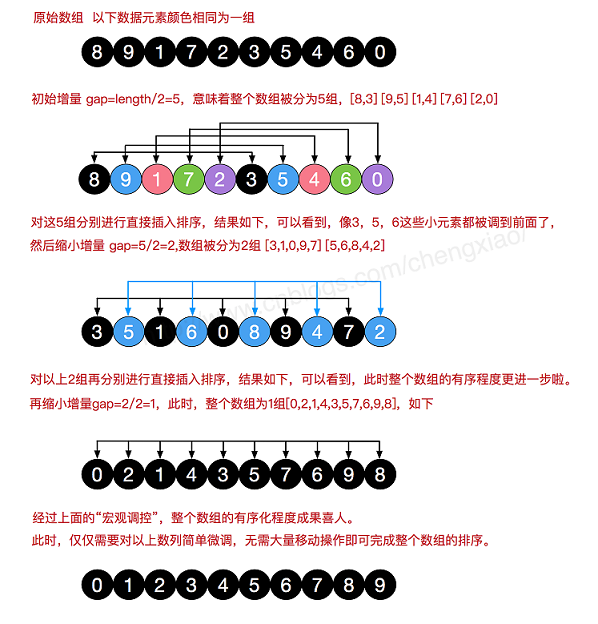
3. Code example
There are two ways to sort.
① Hill sort (bubble sort)
//Shell Sort
// Use step-by-step derivation to write Hill sort
// In Hill sorting, the exchange method is adopted for the insertion of ordered sequences,
// Idea (algorithm) = = > code
public static void shellSort(int[] arr){
// Based on the previous step-by-step analysis, cyclic processing is used
for(int step = arr.length/2;step>0;step /= 2 ){
for (int i = step; i < arr.length; i++) {
// Traverse all elements in each group (a total of step groups, with elements in each group), step
for (int j = i - step; j >= 0; j -= step) {
// If the current element is larger than the element after adding the step size, it indicates the exchange
if (arr[j] > arr[j + step]) {
int temp = arr[j];
arr[j] = arr[j + step];
arr[j + step] = temp;
}
}
}
}
}
Speed test:
Bubble Fisher sort: 120000 data, 11 seconds
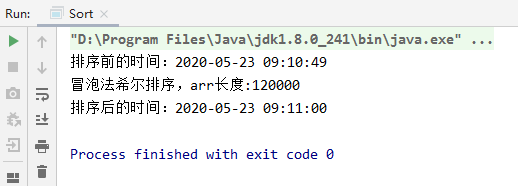
② Hill sort (insert sort)
//Optimize Hill sort of exchange - > insert method
public static void shellSort2(int[] arr) {
// Increment step, and gradually reduce the increment
for (int step = arr.length / 2; step > 0; step /= 2) {
// From the step element, directly insert and sort the groups one by one
for (int i = step; i < arr.length; i++) {
int j = i;
int temp = arr[j];
if(arr[j]<arr[j-step]){
while (j - step >= 0&&temp<arr[j-step]){
arr[j] = arr[j-step];
j -= step;
}
arr[j] = temp;
}
}
}
Speed test:
Insert Fasher sort: 12000000 data, 4 seconds, amazing
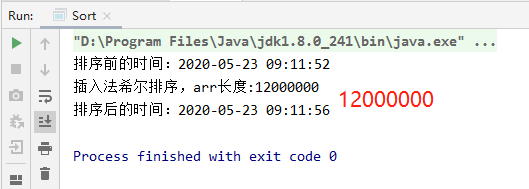
(5) Quick sort
1. Basic thought
The records to be arranged are divided into two independent parts by one-time sorting. If the keywords of one part of the records are smaller than those of the other part, the two parts of the records can be sorted respectively to achieve the whole sorting process.
2. Renderings

3. Algorithm description
-
Quick sort uses divide and conquer to divide a string into two substrings;
-
Find a datum point and temporarily select the middle point as the datum point;
-
Reorder the sequence. The smaller than the reference value is placed in front of the reference point and the larger is placed behind the reference point;
-
Recursively sort the subsequence less than the reference value and the subsequence greater than the reference value;
4. Code example
//Quick sort
public static void quickSort(int[] arr,int left, int right) {
int l = left; //Left subscript
int r = right; //Right subscript
//pivot axis value
int pivot = arr[(left + right) / 2];
int temp = 0; //Temporary variable, used in exchange
//The purpose of the while loop is to put smaller than the pivot value to the left
//Larger than pivot value to the right
while( l < r) {
//Keep looking on the left side of pivot, and exit only after finding a value greater than or equal to pivot
while( arr[l] < pivot) {
l += 1;
}
//Keep looking on the right side of pivot, and exit only after finding a value less than or equal to pivot
while(arr[r] > pivot) {
r -= 1;
}
//If l > = R, it indicates that the left and right values of pivot are all on the left
//Less than or equal to the pivot value, and all on the right are greater than or equal to the pivot value
if( l >= r) {
break;
}
//exchange
temp = arr[l];
arr[l] = arr[r];
arr[r] = temp;
//If after the exchange, it is found that this arr[l] == pivot value is equal to r --, move forward
if(arr[l] == pivot) {
r -= 1;
}
//If after the exchange, it is found that the arr[r] == pivot value is equal to l + +, move it back
if(arr[r] == pivot) {
l += 1;
}
}
// If l == r, it must be l++, r --, otherwise stack overflow occurs
if (l == r) {
l += 1;
r -= 1;
}
//Left recursion
if(left < r) {
quickSort(arr, left, r);
}
//Recursive right
if(right > l) {
quickSort(arr, l, right);
}
}
5. Speed test
Quick sort: 12000000 data, 1 second, go against the sky
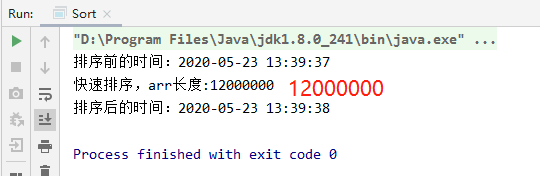
(6) Merge sort
1. Basic thought
Merging and sorting adopts the classical divide and conquer strategy. The divide and conquer method divides the problem into some small problems and then solves them recursively. The stage of governance is to repair the answers obtained in the stages, that is, divide and conquer.
2. Renderings
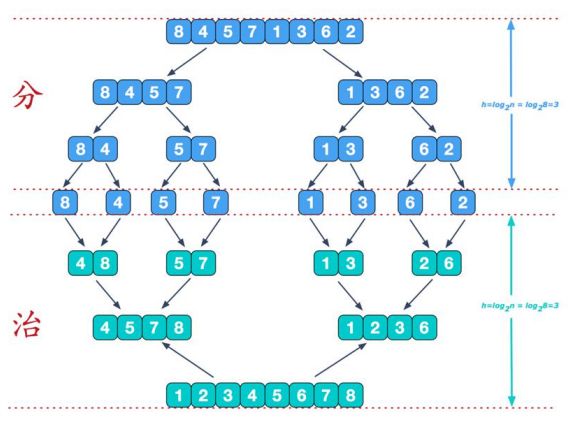
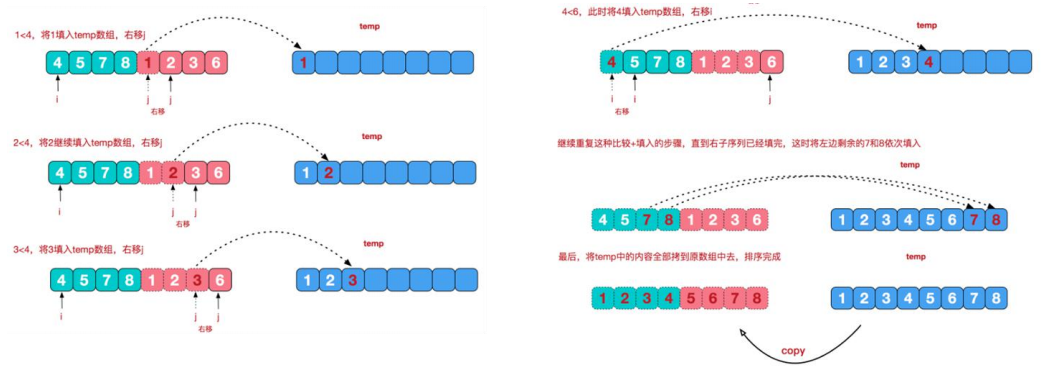
3. Code implementation
//Merge sort
public static void mergerSort(int[] arr,int left,int right,int[] temp){
if(left<right){
//Intermediate index
int middle = (left + right)/2;
//Decompose recursively to the left
mergerSort(arr,left,middle,temp);
//Decompose recursively to the right
mergerSort(arr,middle + 1,right,temp);
//merge
merger(arr, left, middle, right, temp);
}
}
# summary
From basic to advanced and then to actual combat, this paper goes from shallow to deep MySQL Speak clearly and plainly, this should be the best I have seen so far MySQL I believe that if you read this note carefully, you will be able to solve both the problems encountered at work and the questions asked by the interviewer!
**[CodeChina Open source project: [first tier big factory] Java Analysis of interview questions+Core summary learning notes+Latest explanation Video]](https://codechina.csdn.net/m0_60958482/java-p7)**
**MySQL50 Arrangement of high frequency interview questions:**
//Merge sort
public static void mergerSort(int[] arr,int left,int right,int[] temp){
if(left<right){
//Intermediate index
int middle = (left + right)/2;
//Decompose recursively to the left
mergerSort(arr,left,middle,temp);
//Decompose recursively to the right
mergerSort(arr,middle + 1,right,temp);
//merge
merger(arr, left, middle, right, temp);
}
}
# summary
From basic to advanced and then to actual combat, this paper goes from shallow to deep MySQL Speak clearly and plainly, this should be the best I have seen so far MySQL I believe that if you read this note carefully, you will be able to solve both the problems encountered at work and the questions asked by the interviewer!
**[CodeChina Open source project: [first tier big factory] Java Analysis of interview questions+Core summary learning notes+Latest explanation Video]](https://codechina.csdn.net/m0_60958482/java-p7)**
**MySQL50 Arrangement of high frequency interview questions:**
