subject

For the head node of the order linked list, please reverse the linked list and return the head node of the reversed linked list.

Example 1:

Input: head = [1,2,3,4,5]
Output:[5,4,3,2,1]

Example 2:

Input: head = [1,2]
Output:[2,1]

Example 3:

Input: head = []
Output:[]

Problem solution 1 (recursive method)

Problem solution

Train of thought analysis

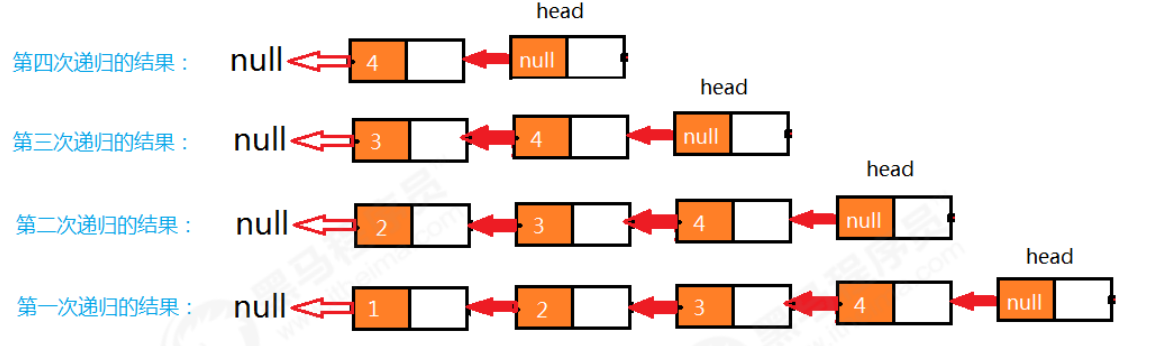
Recursive inversion actually starts from the first node of the original linked list to store data, and recursively calls to reverse each node in turn until the last node is reversed, and the whole linked list is reversed. The following is an example of a node with Sentry (similar to a node without sentry)

Original linked list

step

1. . Call the reverse(Node curr) method to reverse each node, starting from the node of element 1;
2. . If it is found that there is a next node in curr, recursively call reverse(curr.next) to reverse the next node;
3. . The final recursive exit is element 4 node, because it has no next element. When it reaches the exit, there are two ways (with sentry node and without sentry node)
   • Sentinel node: let the head (sentinel node) point to the element 4 node; 4 recursive calls in total
   • Node without sentry: let 4 nodes point to 3 nodes and call recursively for 3 times
4. Recursive start return

Recursive process with sentinel node

code implementation

public class Solution {

    public  ListNode reverseList1(ListNode head) {
        /* The condition judgment will be made every time of recursion
        head == null This is to prevent the linked list from being empty when the reverseList is called through the object for the first time (the recursion has not started yet)
        head.next == null Determines whether the head is the last node in each recursion. If so, it returns (recursion exit)*/
        if (head == null || head.next == null) {
            return head;
        }
       	// Recursion: adjust yourself repeatedly until there is a return value, that is, when you get to the tail node, you return to the tail node (recursion exit). preNode is always the tail node (it will become the head node)
        ListNode preNode = reverseList1(head.next);
        // Make the next node of the current node point to the current node (reverse)
        head.next.next = head;
        // Make the next node of the current node null (its next node has pointed to it in the previous step, that is, the linked list is not broken
        head.next = null;
        return preNode;
    }
}

Node class

public class ListNode<T> {

    T val;
    ListNode next;

    public ListNode() {

    }

    public ListNode(T val) {
        this.val = val;
    }

    public ListNode(T val, ListNode next) {
        this.next = next;
    }
}

Test code

public class Test {

    @org.junit.Test
    public void test1() {
        ListNode<Integer> head = new ListNode<>(1);
        ListNode<Integer> list2 = new ListNode<>(2);
        ListNode<Integer> list3 = new ListNode<>(3);
        ListNode<Integer> list4 = new ListNode<>(4);
        ListNode<Integer> list5 = new ListNode<>(5);
        head.next = list2;
        list2.next = list3;
        list3.next = list4;
        list4.next = list5;
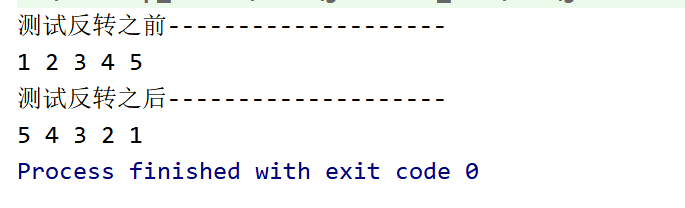
        System.out.println("Before test reversal--------------------");
        ListNode h1 = head;
        while (h1 != null) {
            System.out.print(h1.val + " ");
            h1 = h1.next;
        }
        System.out.println();
        System.out.println("After test reversal--------------------");
        ListNode h2 = new Solution().reverseList1(head);
        while (h2!= null) {
            System.out.print(h2.val + " ");
            h2 = h2.next;
        }
    }
}

test result

Complexity analysis
Suppose the linked list is n

Time complexity: recursive call is equivalent to traversing a linked list, so the time complexity is O(n)
Spatial complexity: n nodes need to be declared in the recursive call process, so the spatial complexity is O(n);

Problem solution 2 (iterative method)

Train of thought analysis

The iterative method is to let each node point to its previous node when traversing the linked list. Because the one-way linked list has only suffix pointer and no prefix pointer, it is necessary to store the information of the previous node during traversal. If the first node has no previous node, it points to null as the tail node, and let each node point to its previous node, You need to store the next node information of this node to prevent the linked list from breaking

step

1. Declare three nodes curr, pre and next. Curr stores the currently traversed node, pre stores the previous node of the current node, and next stores the next node of the current node
2. Traversal linked list
   • The traversal process first stores the next node of the current node
   • Then let the current node point to its previous node
   • Reset pre by making the current node the previous node of its next node
   • Let the next node of the current node be the current node and reset curr;

code implementation

public class Solution {

    public ListNode reverseList2(ListNode head) {
        // Declare a node to store the current node
        ListNode curr = head;
        // Declare a node and store the previous node of the current node
        ListNode pre = null;
        // Traverse the linked list, and the loop termination condition is that the current node is the tail node
        while (curr != null) {
            // Stores the next node of the current node
            ListNode next = curr.next;
            // The next node of the current node points to the previous node of the current node
            curr.next = pre;
            // Reset the previous node of the current node and make the current node the previous node of the next node of the current node
            pre = curr;
            // Reset the current node and make the next node of the current node as the current node
            curr = next;
        }
        return pre;
    }
}

Complexity analysis

Suppose the length of the current linked list is n

Time complexity: the linked list needs to be traversed, so the time complexity is O(n)
Spatial complexity: three nodes curr, pre and next are declared, so the spatial complexity is O(1)