
Welcome back to: meet blue bridge, meet you, not negative code, not negative Qing!
catalogue
1, What is dynamic programming DP
Typical example 1 Fibonacci sequence
Typical example 2: climbing stairs (frogs jumping steps)
Typical example 3 N th teponacci number
Typical example 5 Dominoes problem
Typical example 6 Yang Hui triangle
Typical example 7 Digital triangle
4, Blue bridge conclusion: meet blue bridge, meet you, not negative code, not negative Qing.
[preface]
Before learning dynamic programming, we must first master memory search and recursion. After these two things are done well, it will be much easier to face dynamic programming! OK, let's introduce these two pieces to the iron juice in detail. Let's go.

Ha ha, yesterday, in the group found this watch purse, feel very interesting, specially put here skin, hey hey, this really need to start.
1, What is dynamic programming DP
Dynamic programming (DP) is a method to solve complex problems by decomposing the original problem into relatively simple subproblems
Dynamic programming is often applicable to problems with overlapping subproblems and optimal substructures, and records the results of all subproblems. Therefore, the time of dynamic programming method is often much less than that of violent recursive solution.
The problem solved by dynamic programming has an obvious feature. Once a sub problem is solved, it will not be modified in the future calculation process. This feature is called no aftereffect. The process of solving the problem forms a directed acyclic graph. Dynamic programming only solves each subproblem once, which has the function of natural pruning, so as to reduce the amount of calculation.
Dynamic programming has two ways to solve problems: bottom-up and top-down. Top down is memory search, and bottom up is recursion.
OK, so the memory search and recursion mainly explained in this article will come to the surface. Let's introduce them in detail below (please rest assured that dynamic programming will be explained in detail later. This part is both important and difficult, so it needs to be understood slowly.)
2, Memory search
The essence of memory search: dynamic programming.
Memory search is an implementation of dynamic programming. Memory search realizes dynamic programming by search, so memory search is dynamic programming.
put questions to:
What is memory search?
answer:
As the name suggests, memorized search must have something to do with "search". The recursion, DFS and BFS explained earlier must be almost mastered by everyone. Their biggest disadvantage is: low efficiency! The reason is that overlapping subproblems are not handled well. So for memory search, although it adopts the form of search, it also has the idea of recursion in dynamic programming. Coincidentally, it integrates these two methods well, which is simple and practical.
Mnemonic search, also known as mnemonic recursion, is actually to find many repeated subproblems when dismantling molecular problems, and then solve them and record them later. When you need to solve a sub problem of the same scale in the future, read the answer directly.
In fact, we can simply think that memory search is simple DP, because it is too similar.
The following four examples are explained in detail to let you deeply understand the above concepts:
Typical example 1 Fibonacci sequence
Original title link: Force buckle
Title Description:
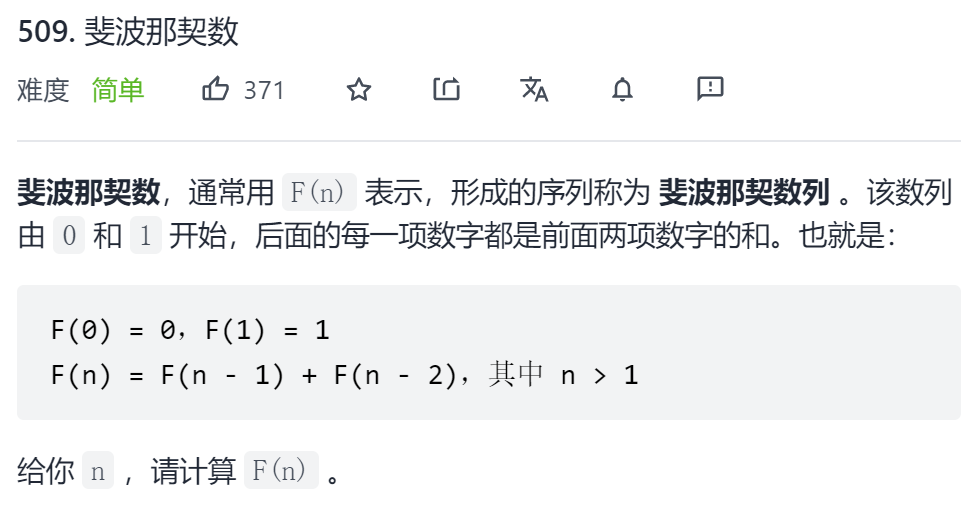
Example 1:
Input: 2 Output: 1 Explanation: F(2) = F(1) + F(0) = 1 + 0 = 1
Example 2:
Input: 3 Output: 2 Explanation: F(3) = F(2) + F(1) = 1 + 1 = 2
Method 1: violence recursion
Code execution:
class Solution {
public:
int fib(int n){
//Method 1: violence recursion
//Find boundary
if(n == 0){
return 0;
}
if(n == 1){
return 1;
}
return fib(n - 1) + fib(n - 2);
}
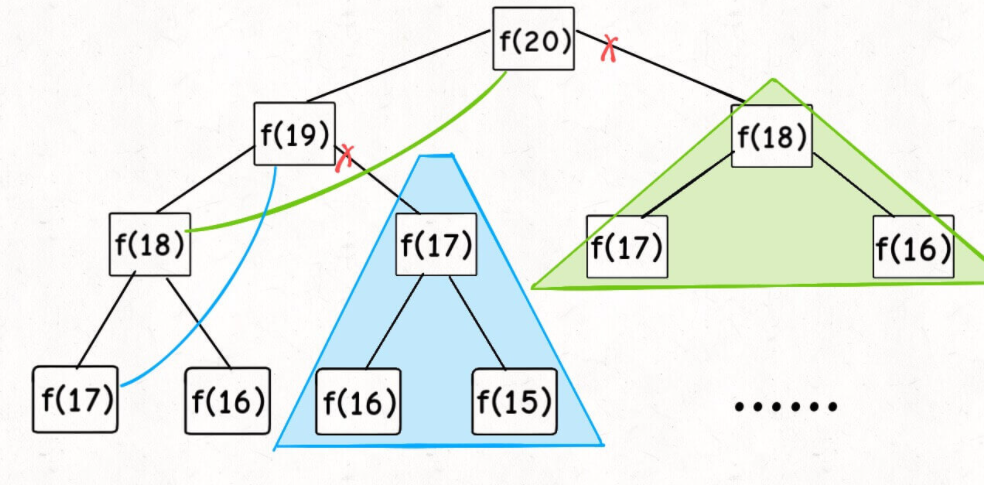
};Needless to say, school teachers seem to take this example when talking about recursion. We also know that writing code like this is simple and easy to understand, but it is very inefficient. Where is the inefficiency? Suppose n = 20, draw a recursive tree:

Obviously, a lot of repeated calculations have been carried out. Although this problem is a good example to explain recursion, it is unwise to use recursion in practical application. Therefore, we need to introduce a recursion with "Memo", that is, the memory search mentioned earlier. Let's see how to operate it:
Method 2: memory search
That is, the reason for the low efficiency is repeated calculation, so we can make a "Memo". After calculating the answer to a sub question each time, don't rush back, write it down in the "Memo" and then return; Every time you encounter a sub problem, check it in the "Memo". If you find that you have solved the problem before, you can use the answer directly instead of taking time to calculate.
Generally, an array is used as the memo. Of course, you can also use a hash table (Dictionary). The idea is the same.
In this way, there is no need for repeated calculation. Compared with the previous violent recursion, it is much more efficient and wise, and it is easy to understand. I don't believe you see:
Code execution:
class Solution {
public:
int fib(int n){
//Method 3: memory search (simple DP)
//Find boundary
if(n == 0){
return 0;
}
if(n == 1){
return 1;
}
//An integer array of size (n+1) needs to be defined and initialized to 0
//It's n+1 because you want to use the subscript n
vector<int> dp(n+1, 0);
dp[0] = 0;
dp[1] = 1;
for(int i = 2; i < n+1; i++)
{
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
};Of course, there is also such deformation. There is one more requirement. It is very simple. Let's have a look:
Deformation problem
Code execution:
//Find boundary
if(n == 0)
return 0;
if(n == 1)
return 1;
vector<int> dp(n + 1, 0);//Open up an integer array of size n+1 (because the subscript n needs to be used) and initialize it to 0
dp[0] = 0;
dp[1] = 1;
for(int i = 2; i < n+1; i++)
{
dp[i] = dp[i - 1] + dp[i - 2];
dp[i] = dp[i] % 1000000007;
}
return dp[n];
}In fact, this solution is very similar to iterative dynamic programming, except that this method is called "top-down" and dynamic programming is called "bottom-up".
What is "top-down"?
Note that the recursive tree (or graph) we just drew extends from top to bottom. It is gradually decomposed from a large-scale original problem, such as f(20), down to the two base case s of f(1) and f(2), and then returns the answer layer by layer, which is called "top-down".
What is "bottom up"?
On the contrary, we directly start from the bottom, the simplest and the smallest problem scale, f(1) and f(2), until we push to the answer we want, f(20). This is the idea of dynamic programming, which is why dynamic programming generally breaks away from recursion and completes the calculation by cyclic iteration.
Typical example 2: climbing stairs (frogs jumping steps)
Original title link: Force buckle
Title Description:
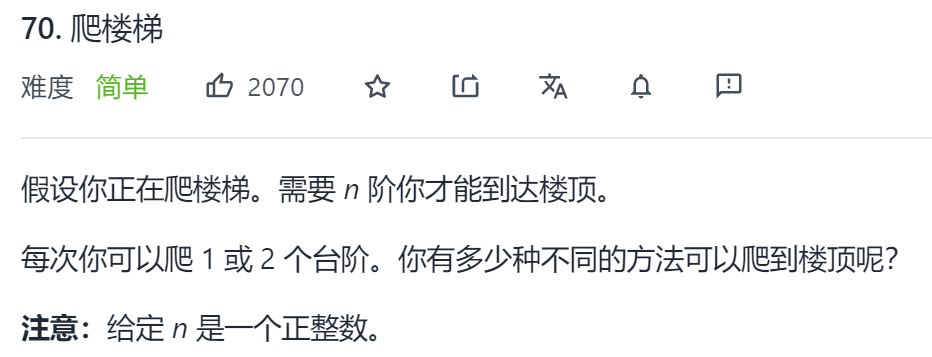
Example 1:
Input: 2 Output: 2 Explanation: there are two ways to climb to the roof. 1. 1 rank + 1 rank 2. 2 rank
Example 2:
Input: 3 Output: 3 Explanation: there are three ways to climb to the roof. 1. 1 rank + 1 rank + 1 rank 2. 1 rank + 2 rank 3. 2 rank + 1 rank
First, analyze the problem:
Note: what is the question?
The question is not how many times you can climb, but how many ways you can reach the last step.
Problem analysis:
When n > 2, there are two different choices for the first climb: one is to climb only one level for the first time. At this time, the number of climbing methods is equal to the number of climbing methods of the remaining (n - 1) steps, that is, f(n - 1); Another option is to climb two steps for the first time. At this time, the number of climbing methods is equal to the number of climbing methods of the remaining (n - 2) steps, that is, f(n - 2)
So there are: f(n) = f(n - 1) + f(n - 2)
When n == 1, there is one climbing method;
When n == 2, there are two climbing methods;
When n == 3, there are three climbing methods;
When n == 4, there are 5 climbing methods.
Yes, this problem is basically the same as the Fibonacci sequence, but this problem needs to be considered. It is not as obvious as the Fibonacci sequence. However, it should be noted that the recursive boundary is still different!
Method 1: violence recursion
Code execution:
class Solution {
public:
int climbStairs(int n) {
//Method 1: violence recursion
//Find boundary
if(n == 1){
return 1;
}
if(n == 2){
return 2;
}
return climbStairs(n - 1) + climbStairs(n - 2);
}
};Method 2: memory search
Code execution:
class Solution {
public:
int climbStairs(int n) {
//Method 2: memory search (simple DP)
//Find boundary
if(n == 1){
return 1;
}
if(n == 2){
return 2;
}
//Define an integer array of size n+1 and initialize it to 0
vector<int> dp(n+1, 0);
dp[1] = 1;
dp[2] = 2;
for(int i = 3; i < n+1; i++)
{
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
};Deformation problem
In fact, there is one more requirement
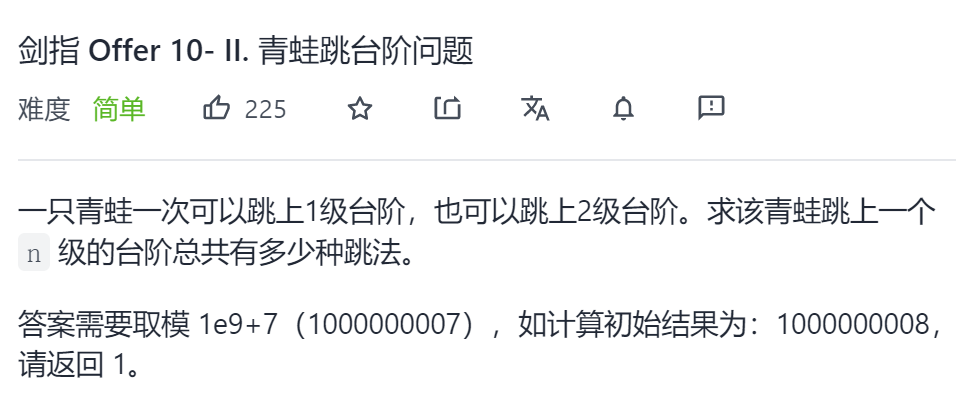
Code execution:
class Solution {
public:
int numWays(int n) {
//Find boundary
if(n == 0 || n == 1)
return 1;
if(n == 2)
return 2;
vector<int> dp(n+1, 0);
dp[1] = 1;
dp[2] = 2;
for(int i = 3; i < n+1; i++)
{
dp[i] = dp[i - 1] + dp[i - 2];
dp[i] %= 1000000007;
}
return dp[n];
}
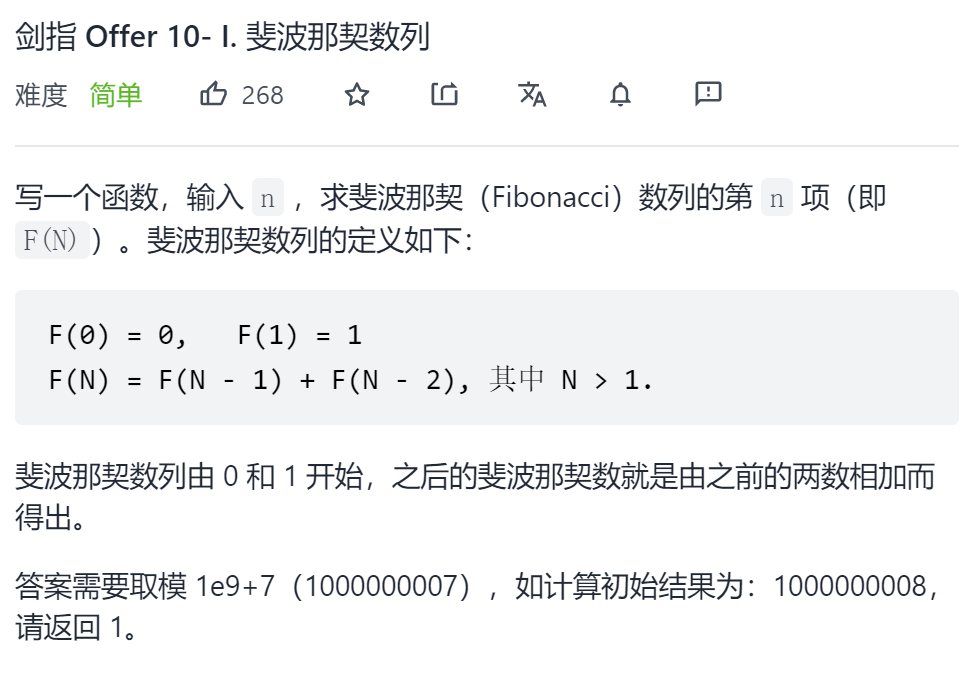
};Typical example 3 N th teponacci number
Original title link: Force buckle
Title Description:
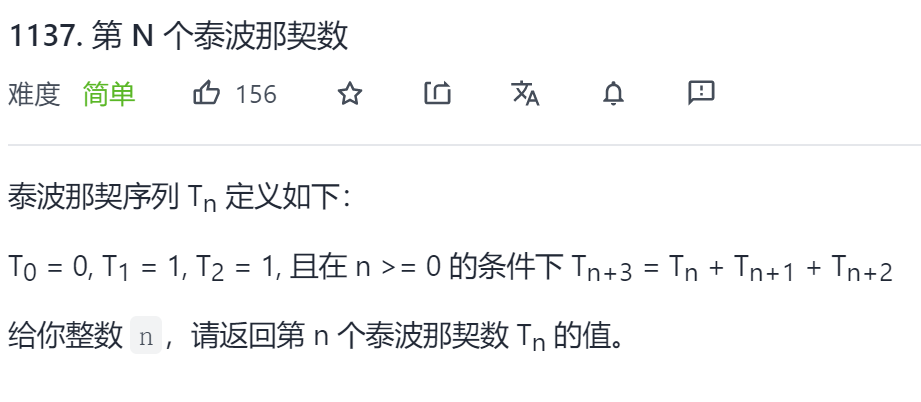
Example 1:
Input: n = 4 Output: 4 Explanation: T_3 = 0 + 1 + 1 = 2 T_4 = 1 + 1 + 2 = 4
Example 2:
Input: n = 25 Output: 1389537
Code execution:
class Solution {
public:
int tribonacci(int n) {
//Find boundary
if(n == 0)
return 0;
if(n == 1 || n == 2)
return 1;
//Define an integer array of size n+1 and initialize it to 0
vector<int> dp(n+1, 0);
dp[0] = 0;
dp[1] = 1;
dp[2] = 1;
for(int i = 3; i < n+1;i++)
{
dp[i] = dp[i - 3] + dp[i - 2] + dp[i - 1];//Recurrence formula
}
return dp[n];
}
};The above three questions are very simple. If you understand the above questions, the following questions will be very easy.
Typical example 4 Function
Original title link: Function - Luogu
Title Description:

Input format:
The input has several lines. And end with − 1, − 1, − 1.
Ensure that the number entered is between [− 92233720368547758089223372036854775807] and is an integer.
Output format
Output several lines, each in the format of w(a, b, c) = ans
Idea:
This topic focuses on understanding the meaning of the topic. The topic is not difficult, but you should read the topic several times.
Code execution:
#include <stdio.h>
#define LL long long
LL dp[25][25][25];
LL w(LL a, LL b, LL c)
{
//Judgment of two special cases
if(a <= 0 || b <= 0 || c <= 0)
return 1;
if(a > 20 || b > 20 || c > 20)
return w(20, 20, 20);
if(a < b && b < c)
{
if(dp[a][b][c-1] == 0)
{
dp[a][b][c-1] = w(a, b, c-1);
}
if(dp[a][b-1][c-1] == 0)
{
dp[a][b-1][c-1] = w(a, b-1 ,c-1);
}
if(dp[a][b-1][c] == 0)
{
dp[a][b-1][c] = w(a, b-1, c);
}
dp[a][b][c] = dp[a][b][c-1] + dp[a][b-1][c-1] - dp[a][b-1][c];
}
else
{
if(dp[a-1][b][c] == 0)
{
dp[a-1][b][c] = w(a-1, b, c);
}
if(dp[a-1][b-1][c] == 0)
{
dp[a-1][b-1][c] = w(a-1, b-1 ,c);
}
if(dp[a-1][b][c-1] == 0)
{
dp[a-1][b][c-1] = w(a-1, b, c-1);
}
if(dp[a-1][b-1][c-1] == 0)
{
dp[a-1][b-1][c-1] = w(a-1, b-1, c-1);
}
dp[a][b][c] = dp[a-1][b][c] + dp[a-1][b][c-1] + dp[a-1][b-1][c] - dp[a-1][b-1][c-1];
}
return dp[a][b][c];
}
int main()
{
LL a, b, c;
while(scanf("%lld%lld%lld", &a, &b, &c) != EOF)
{
if(a == -1 && b == -1 && c == -1)
return 0;//When the value entered is - 1 - 1, the cycle ends directly
printf("w(%lld, %lld, %lld) = ", a, b, c);
printf("%lld\n", w(a, b, c));
}
}
3, Recurrence
When you see "recursion", you can certainly think of "recursion". OK, let's explain in detail the differences between recursion and recursion.
1. Recursion
If you don't master the recursive part well, you can take a look at my previous blog. The basic concepts are explained in detail, and there are a lot of exercises.
Recursion is a kind of algorithm that transforms a big problem into a small problem, constantly calls itself or is indirectly called.
1. The key of recursive algorithm is to find the relationship between large problems and small problems -- that is, to find repetition, so as to reduce the scale of large problems until they can be solved directly.
2. Another key point of recursive algorithm is the termination condition -- finding the boundary, which is very important.
Sometimes, the efficiency of recursive algorithm will be very low. At this time, you can use the memory search mentioned above, that is, establish an array to record the answers obtained by each recursion. In this way, if you want to continue to use this value later, you don't have to calculate again, and the problem of repeated calculation is avoided.
2. Recurrence
Some definitions and solutions refer to the blog link:
Recursion and recursion are very similar.
Recursion is to divide the problem into several steps. There is a certain quantitative relationship between each step or between this step and the previous steps. The value of this item can be expressed by the values of the previous items, so that a complex problem can be turned into many small problems.
The recursive algorithm pays attention to what kind of recursive state to set, because a good recursive state can make the problem very simple. The most difficult thing is to come up with a recursive formula. Generally, the recursive formula is to think forward from the back and push back.
Typical example 5 Dominoes problem
Title Description:
A rectangular square with 2*n, covered with a 1 * 2 dominoes. Please write a program to output the total number of paving methods for any given n (n > 0).
Idea:
In fact, this problem is very simple. Just find the recurrence formula, which is very similar to the stair climbing problem above. Here's a detailed analysis:
When n = 1, there is only one paving method
When n = 2, as shown in the following figure, there are two kinds of paving: all vertical paving and horizontal paving
When n = 3, all dominoes can be laid vertically, or it can be considered that there is already a vertically laid dominoes in the square, so two horizontal ribs need to be arranged in the square (no repeat method). If two horizontal ribs have been arranged in the square, one vertical ribs must be arranged in the square. As shown in the figure below, there are no other arrangement methods, so the total number of laying methods is expressed as three.
Through the above analysis, it is not difficult to see the law: f(3) = f(1) + f(2)
So we can get the recurrence relation: f(n) = f(n - 1) + f(n - 2)

Code execution:
class Solution {
public:
int brand(int n) {
//Find boundary
if(n == 1){
return 1;
}
if(n == 2){
return 2;
}
//Define an integer array of size n+1 and initialize it to 0
vector<int> dp(n+1, 0);
dp[1] = 1;
dp[2] = 2;
for(int i = 3; i < n+1; i++)
{
dp[i] = dp[i - 1] + dp[i - 2];//Find the recurrence relation
}
return dp[n];
}
};Typical example 6 Yang Hui triangle
Original title link: Force buckle
Title Description:

Example 1:
input: numRows = 5 output: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
Example 2:
input: numRows = 1 output: [[1]]
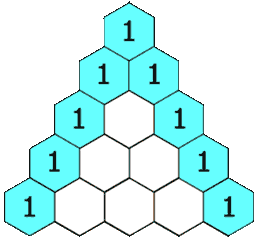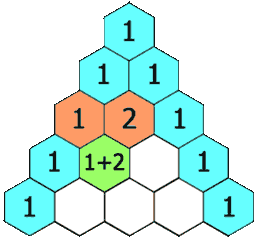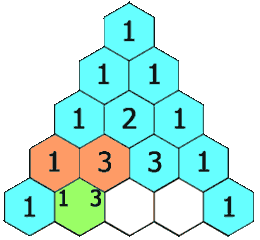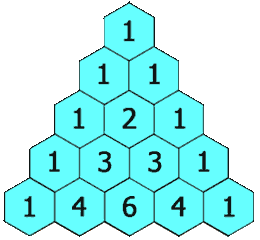
Idea:
This question is relatively simple. It is easy to see the recursive relationship. Starting from the third row and the second column, each number is the sum of the numbers at the top left and right.
Code execution:
class Solution {
public:
vector<vector<int>> generate(int numRows) {
vector<vector<int> >ret(numRows);//Define a two-dimensional array to store the results
//First, assign all the elements of the first and last columns to 1
for(int i = 0; i < numRows; i++)
{
ret[i].resize(i+1);//The function of resize() is to allocate space for a one-dimensional array
ret[i][0] = ret[i][i] = 1;
//There is a recursive relationship from the second column of the third row: ret[i][j] = ret[i+1][j]+ret[i+1][j+1];
for(int j = 1; j < i; j++)
{
ret[i][j] = ret[i-1][j] + ret[i-1][j-1];
}
}
return ret;
}
};It should be noted in the code that resize() in vector reallocates space.
Typical example 7 Digital triangle
Original title link: [USACO1.5][IOI1994] Number Triangles - Luogu
Title Description:
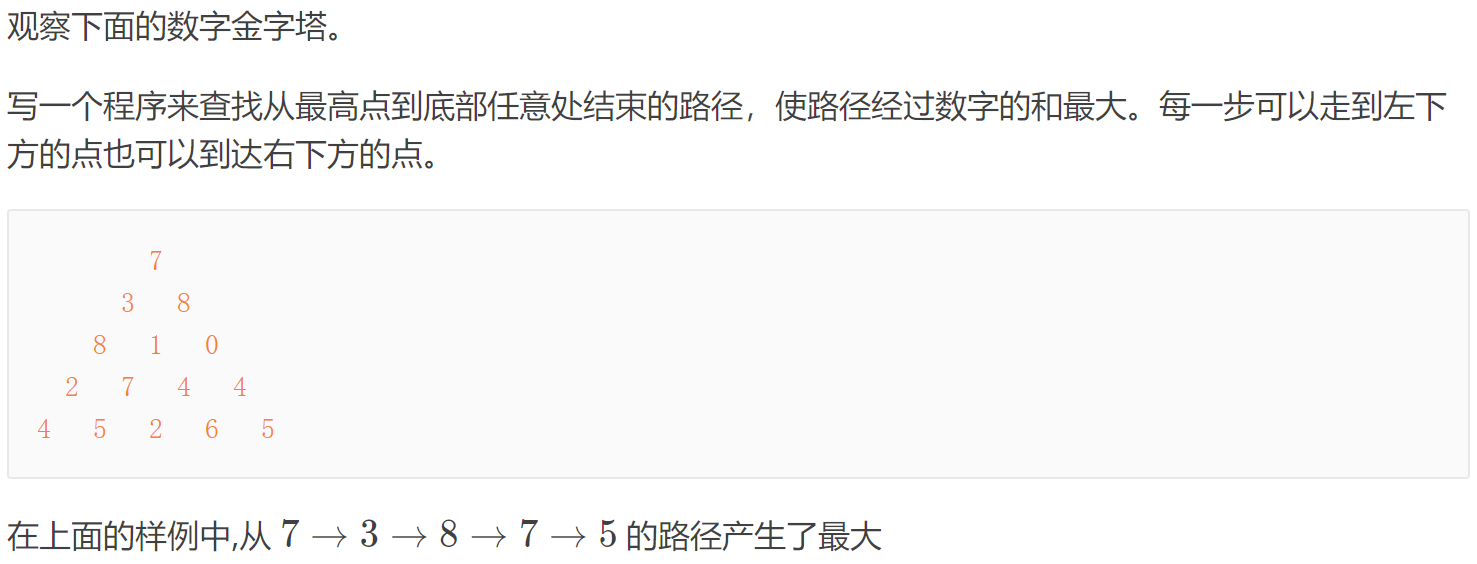
Input format:
The first row is a positive integer n, indicating the number of rows.
Each subsequent row contains an integer in a specific row of this numeric pyramid.
Output format:
A single line containing the largest possible sum.
Data range:
1 ≤ n ≤ 1000, the triangle digital value is within the range of [0100].
Example:
Input:
5 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5
Output:
30
Idea:
This question adopts the backward method:
Suppose func[i][j] represents the sum of the maximum paths from i, j to the last layer
When walking along a path from the top layer to layer I to layer i+1, our choice is to move along the direction of the largest number in the next two feasible paths, so find out the recursive relationship: func[i][j] += max(func[i+1][j],func[i+1][j+1]);
Note: func[i][j] represents the value of the current number, and func[i+1][j] and func[i+1][j+1] represent the sum of the maximum paths from i+1,j, i+1,j+1 to the last layer respectively;
Finally func[0][0] is what you want
Code execution:
#include<stdio.h>
#include<algorithm>
using namespace std;
int func[1005][1005] = {0};
int main()
{
int n = 0;
scanf("%d", &n);
int i = 0;
int j = 0;
for(i = 0; i < n; i++)
{
for(j = 0; j <= i; j++)
{
scanf("%d", &func[i][j]);
}
}
//Suppose func[i][j] represents the sum of the maximum paths from i, j to the last layer
//Find out the recurrence relationship: func[i][j]+=max(func[i+1][j],func[i+1][j+1]);
//func[i][j] represents the value of the current number, func[i+1][j] and func[i+1][j+1] represent the sum of the maximum paths from i+1,j, i+1,j+1 to the last layer respectively
//Finally func[0][0] is what you want
for(i = n - 2; i >= 0; i--)
{
for(j = 0; j <= i; j++)
{
func[i][j] += max(func[i+1][j], func[i+1][j+1]);
}
}
printf("%d\n", func[0][0]);
return 0;
}
4, Blue bridge conclusion: meet blue bridge, meet you, not negative code, not negative Qing.
It's time to say goodbye again. The above part is the introduction of dynamic rules, which seems not difficult, but in fact, the difficulty of dynamic programming algorithm is really abnormal, and it will go deep slowly later. However, blue bridge will hardly test the particularly difficult dynamic rules, which are normally simple DP, so there will be a lot of exercises later, focusing on simple DP. OK, that's the end of today. eight hundred and eighty-six
Please brothers and sisters, give me three company~

 https://blog.csdn.net/weixin_57544072/article/details/120836167
https://blog.csdn.net/weixin_57544072/article/details/120836167