Navigation:
1. Insert sorting directly
Idea: it can be understood as inserting the sequence to be arranged into the ordered sequence in turn; Compare from back to front, compare the number to be inserted with the last element of the ordered sequence. If it is larger than the number with insertion, move backward until the first element less than the number to be inserted is found, and put the number with insertion after it;
Dynamic diagram demonstration:
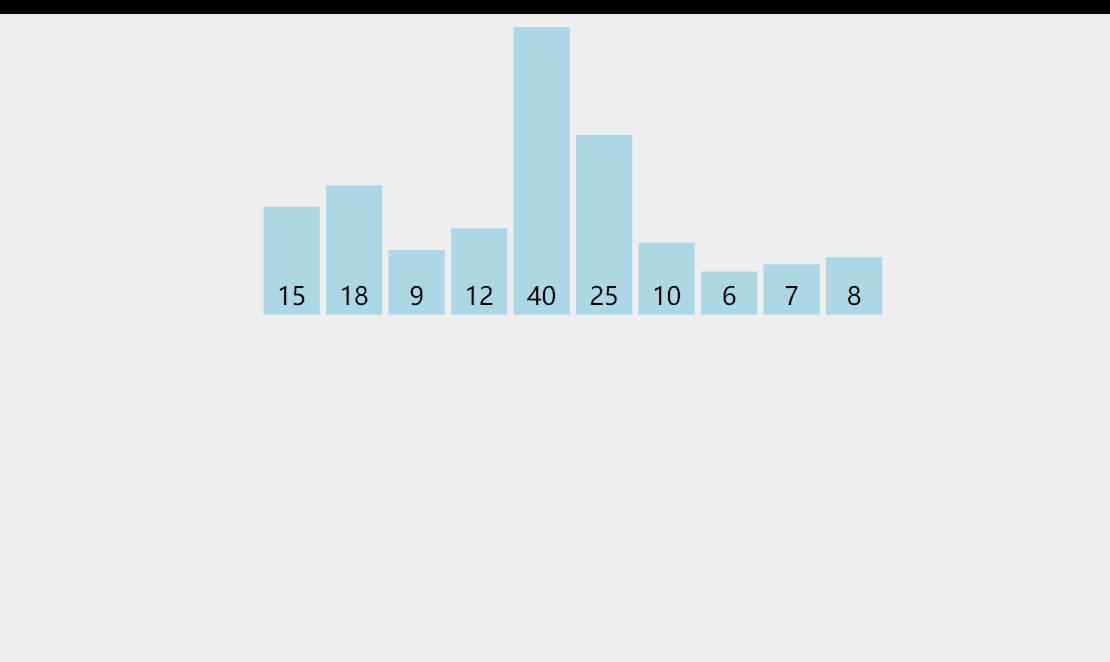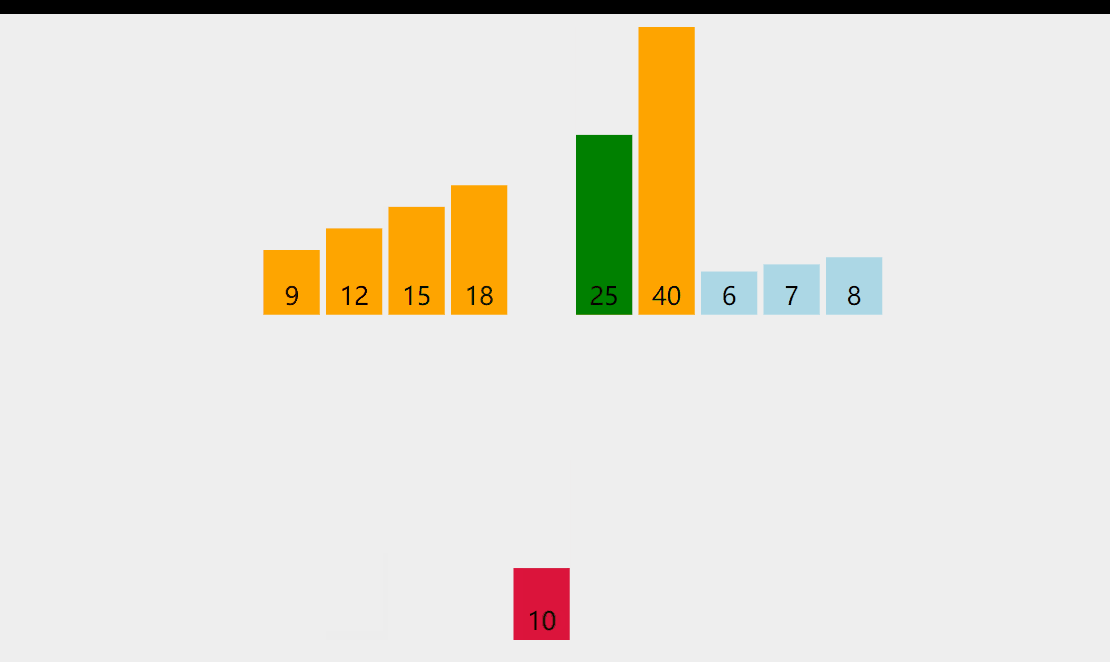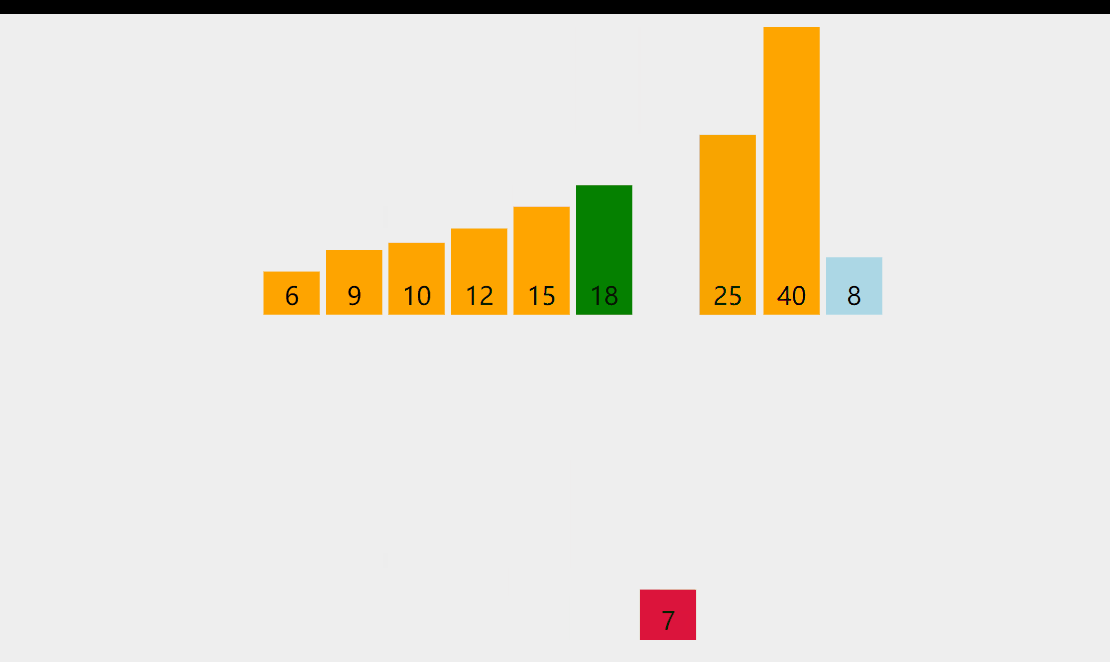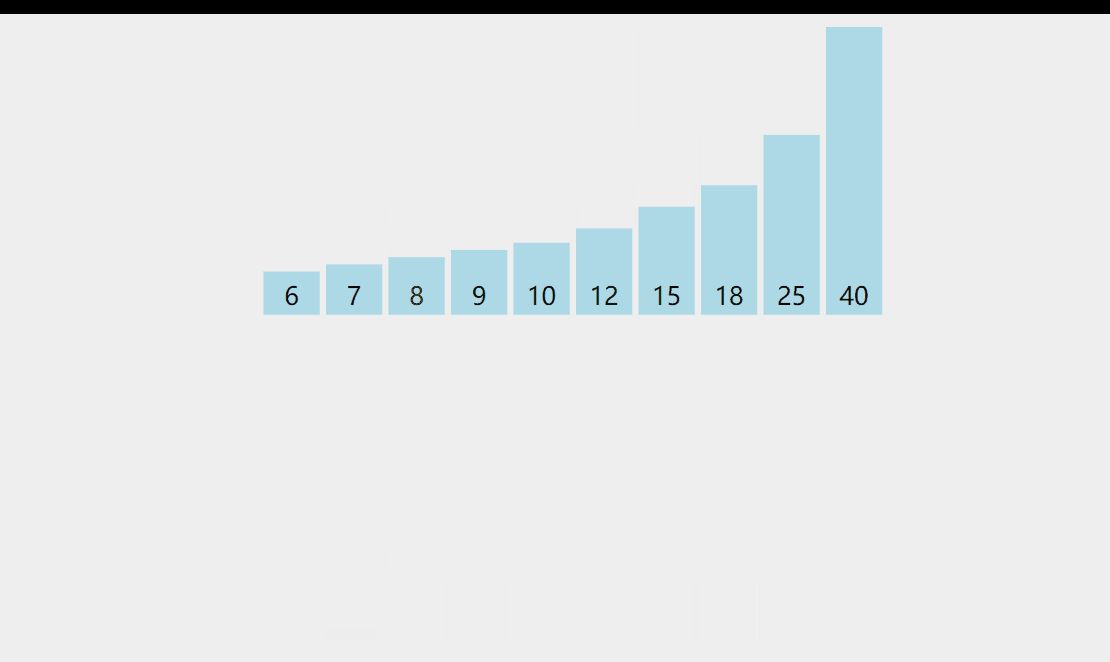
Code example:
/*Insert sort*/
#include<iostream>
using namespace std;
#define N 1000
int a[N]={0};
void InserSort(int *a,int n)
{
for(int i=0;i<n-1;i++)
{
//Records the subscript of the last element of an ordered sequence
int end = i;
//Elements to be inserted
int t = a[end+1];
while(end>=0)
{
//Move back if it is larger than the number inserted
if(t<a[end])
{
a[end+1]=a[end];
end--;
}
//Jump out of the loop if it is smaller than the number of inserts
else
{
break;
}
}
a[end+1]=t;
}
}
int main()
{
int n;
cin>>n;
for(int i=0;i<n;i++)
{
cin>>a[i];
}
//Output array before sorting
cout<<"The array before sorting is:"<<endl;
for(int i=0;i<n;i++)
{
cout<<a[i]<<" ";
}
cout<<endl;
InserSort(a,n);
cout<<"The sorted array is:"<<endl;
for(int i=0;i<n;i++)
{
cout<<a[i]<<" ";
}
return 0;
}Code run result:

2. Hill sort
Idea: Hill sort is also an insert sort, but it is much more efficient than direct insert sort;
Firstly, the whole to be sorted sequence is divided into several subsequences, and then they are directly inserted and sorted respectively. When the whole sequence is basically orderly, the whole to be sorted sequence is inserted and sorted once;
Code display:
/*Shell Sort */
#include<iostream>
using namespace std;
#define N 1000
int a[N]={0};
void ShellSort(int *a,int n)
{
int gap=n;
while(gap>1)
{
//Half gap every time
gap/=2;
//Single pass sorting
for(int i=0;i<n-gap;i++)
{
int end=i;
int t = a[end+gap];
while(end>=0)
{
if(t<a[end])
{
a[end+gap]=a[end];
end-=gap;
}
else
{
break;
}
}
a[end+gap]=t;
}
}
}
int main()
{
int n;
cin>>n;
for(int i=0;i<n;i++)
{
cin>>a[i];
}
cout<<"Before sorting:"<<endl;
for(int i=0;i<n;i++)
{
cout<<a[i]<<" ";
}
cout<<"After sorting:"<<endl;
ShellSort(a,n);
for(int i=0;i<n;i++)
{
cout<<a[i]<<" ";
}
return 0;
}Sort instance:
5
9 85 6 9 2
Before sorting:
9 85 6 9 2 after sorting:
2 6 9 9 85

3. Select Sorting
Idea: traverse the to be sorted (begin=0; begin + +) from the beginning to select the smallest element and the beginning of the sequence for exchange (that is, the element at the position with the index begin is exchanged with the minimum value on the to be sorted element), use end=n-1 to represent the end -- of the last element of the to be sorted element each time, and then drop the band until the end of begin=end;
Dynamic diagram demonstration:
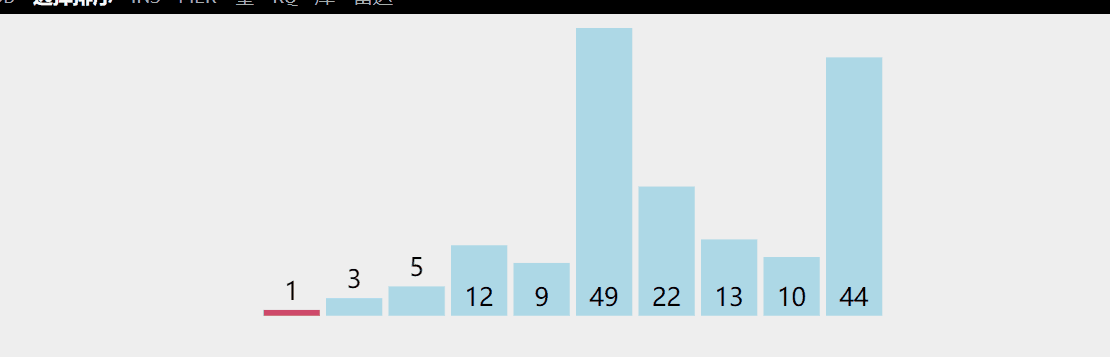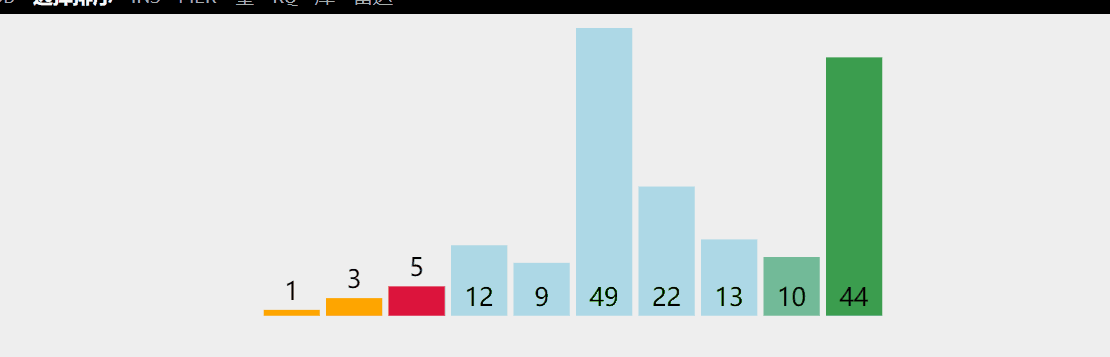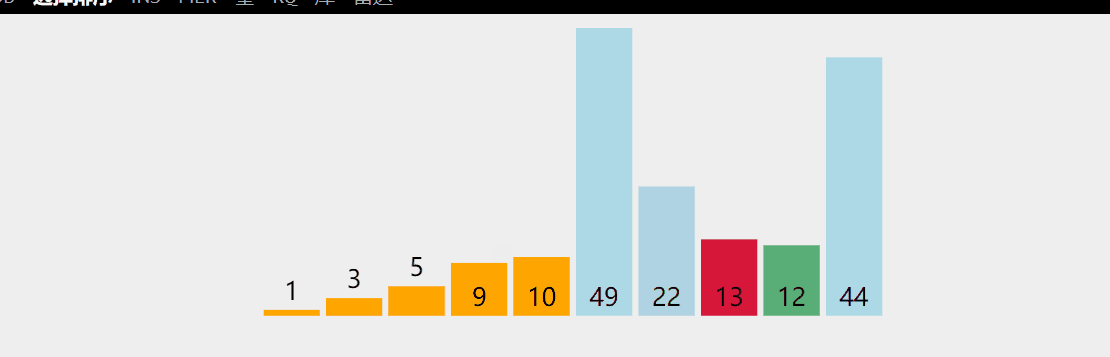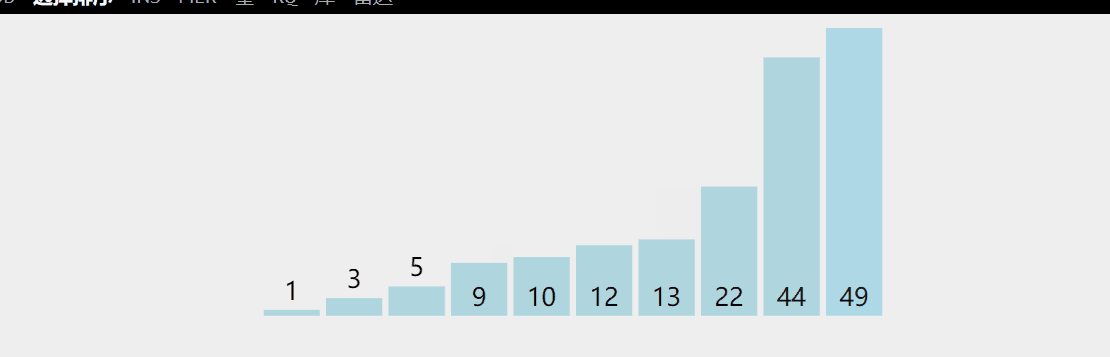
/*Select sort*/
#include<iostream>
using namespace std;
#define N 1000
int a[N]={0};
void swap(int *a,int *b)
{
int t=*a;
*a=*b;
*b=t;
}
void SelectSort(int *a,int n)
{
//Record the subscripts of the first and last numbers of the sorted array
int begin=0,end=n-1;
while(begin<end)
{
//Save the subscript of the maximum and minimum values
int maxid=begin;
int minid=begin;
//Find the subscripts of the maximum and minimum values
for(int i=begin;i<=end;i++)
{
if(a[minid]>a[i])
{
minid=i;
}
if(a[maxid]<a[i])
{
maxid=i;
}
}
//Put the minimum at the beginning
swap(&a[minid],&a[begin]);
if(maxid==begin)
{
maxid=minid;
}
//Put the maximum last
swap(&a[maxid],&a[end]);
begin++;
end--;
}
}
int main()
{
int n;
cin>>n;
for(int i=0;i<n;i++)
{
cin>>a[i];
}
cout<<"Before sorting:"<<endl;
for(int i=0;i<n;i++)
{
cout<<a[i]<<" ";
}
SelectSort(a,n);
cout<<"After sorting:"<<endl;
for(int i=0;i<n;i++)
{
cout<<a[i]<<" ";
}
return 0;
}Sort cases:
10
1 3 5 12 9 49 22 13 10 44
Before sorting:
1 3 5 12 9 49 22 13 10 44 after sorting is:
1 3 5 9 10 12 13 22 44 49
4. Bubble sorting
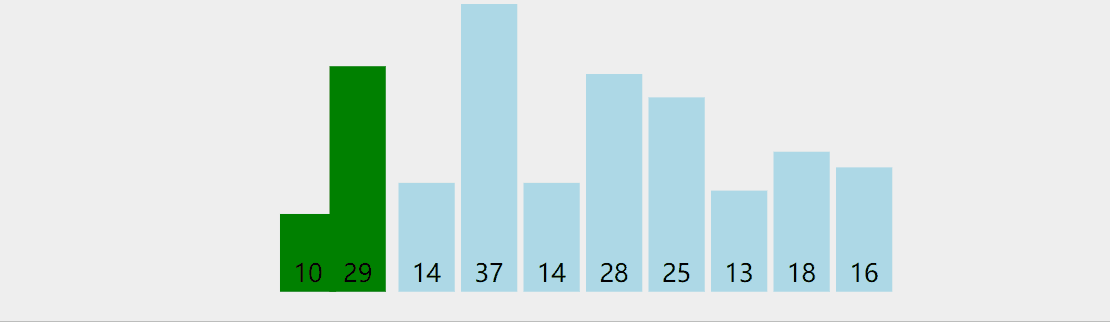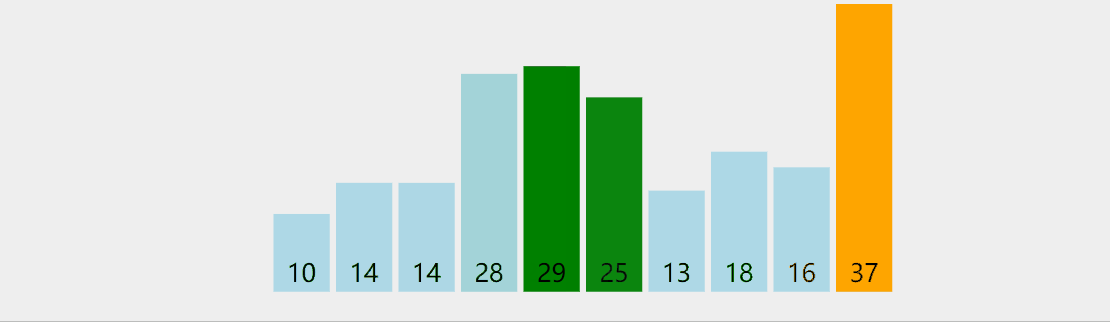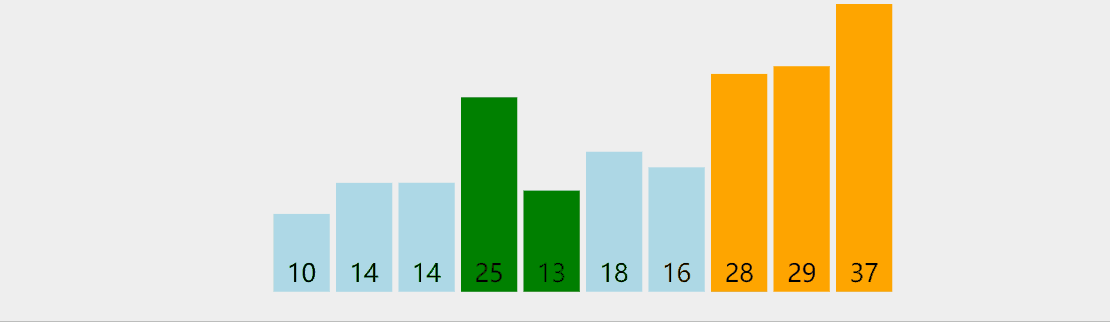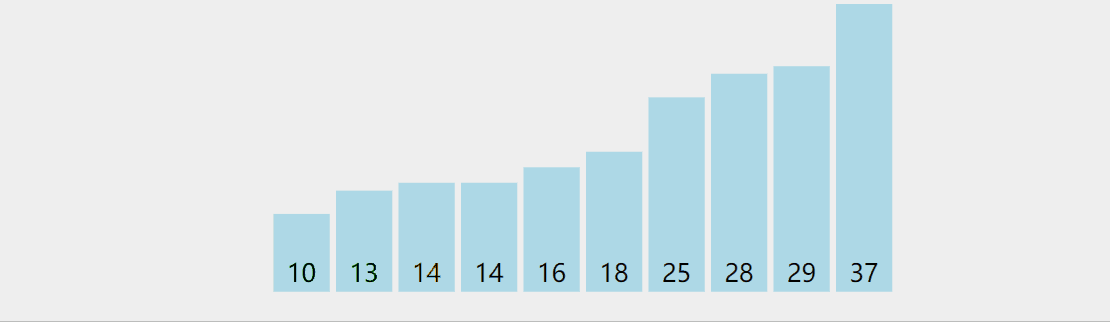
Idea: traverse from the beginning. If the left side is larger than the right side of the two adjacent comparison, exchange. The largest rightmost one in a trip; Traverse n-1 times;
Dynamic diagram demonstration:
/*Bubble sorting*/
#include<iostream>
using namespace std;
#define N 1000
int a[N]={0};
void BubbleSort(int *a,int n)
{
for(int i=0;i<n;i++)
{
for(int j=i+1;j<n;j++)
{
if(a[i]>a[j])
{
int t=a[i];
a[i]=a[j];
a[j]=t;
}
}
}
}
int main()
{
int n;
cin>>n;
for(int i=0;i<n;i++)
{
cin>>a[i];
}
cout<<"Before sorting:"<<endl;
for(int i=0;i<n;i++)
{
cout<<a[i]<<" ";
}
BubbleSort(a,n);
cout<<"After sorting:"<<endl;
for(int i=0;i<n;i++)
{
cout<<a[i]<<" ";
}
return 0;
}5. Heap sorting
Idea:
First, understand the definition of heap: the sequence of n elements {k1,k2,k3, ····, kn} is called heap if and only if the following relationship is satisfied.
If K (I) < = K (2I) & & K (I) < = K (2I + 1) satisfies this relationship, we call it small top pile;
or
If K (I) > = K (2I) & & K (I) > = K (2I + 1) satisfies this relationship, we call it large top reactor;
Heap sorting idea: first, we traverse and store the examples to be sorted according to the binary tree level. How to initialize them into a large top heap or a small top heap according to the conditions that the heap should be concealed. Here, we initialize them into a large top heap, take out the top of the heap and put it at the end of the sequence, move the last element in the heap to the top of the heap, and then convert the sequence into a large top heap; Repeat the above operation to complete the sorting;
Demonstration of creating large top reactor dynamic diagram:
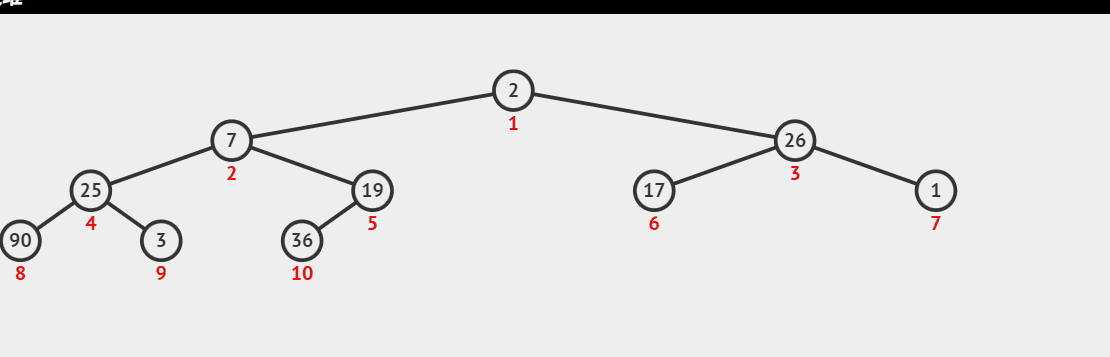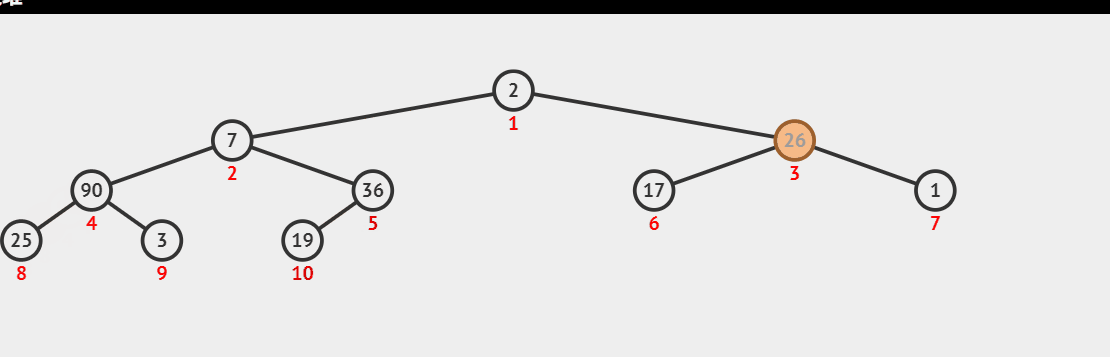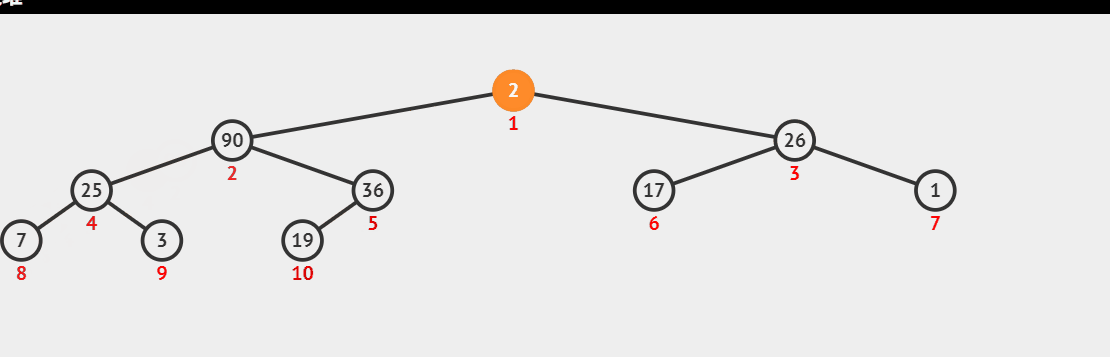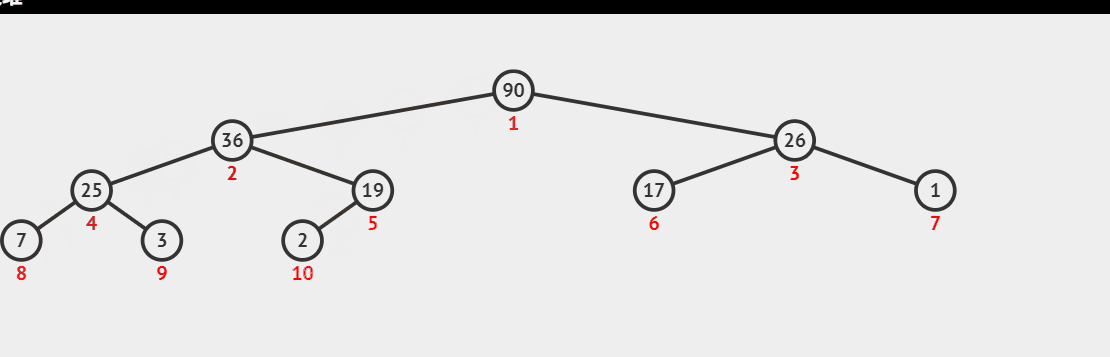
The maximum value of each output is the top of the big top heap, and then take the last element to fill it
Dynamic diagram demonstration (here we output the first three elements 90, 36 and 26 in turn):
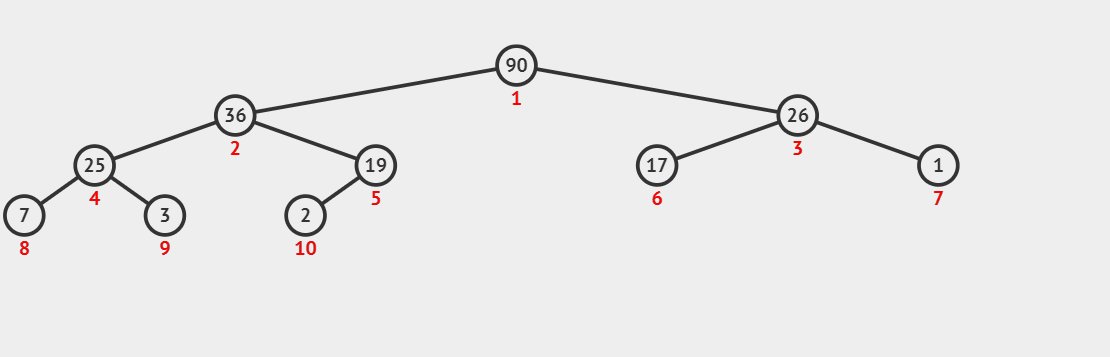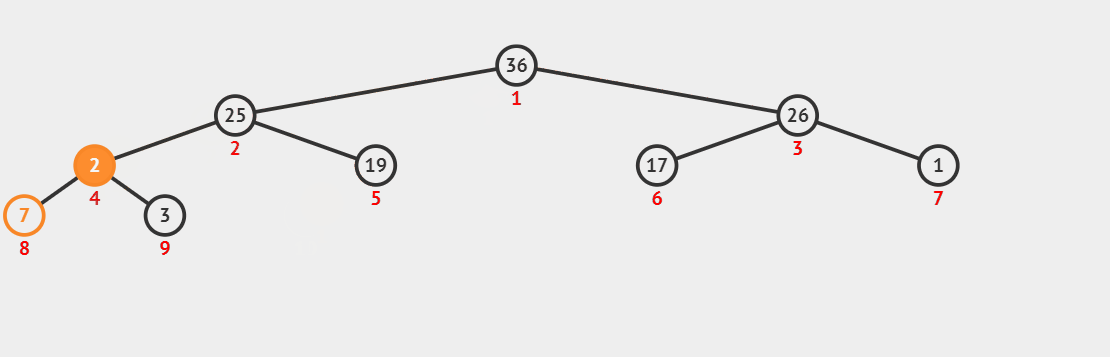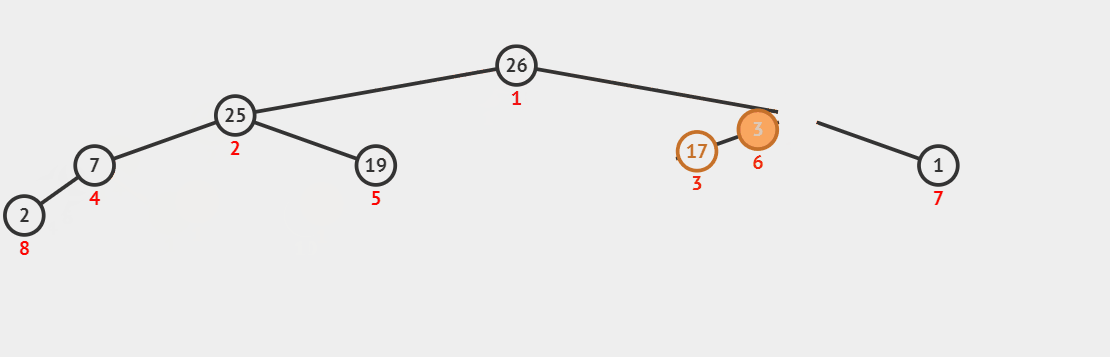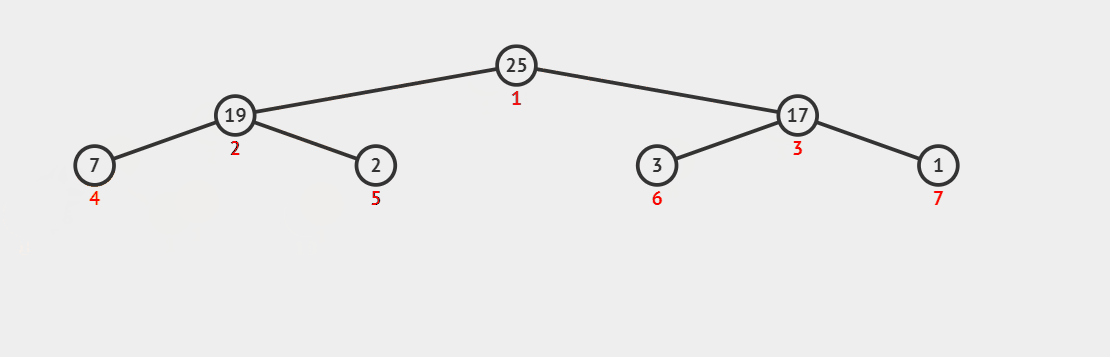
Code supplement:
/*Heap sort*/
#include<iostream>
using namespace std;
#define N 1000
int a[N]={0};
void swap(int a,int b);
void MintoBig(int *a,int i,int n);
void MintoBig(int *a,int i,int n);
void BuildHeap(int *a,int n);
//Define functions for exchange
void swap(int *a,int i,int j)
{
int t=a[i];
a[i]=a[j];
a[j]=t;
}
//Sort from small to large
void MintoBig(int *a,int i,int n)
{
int par=i;
int child=2*i+1;
while(child<n)
{
if(a[child]<a[child+1]&&child+1<n)
{
child++;
}
//If the above conditions for are not met, if child + 1 < n, there is a [child + 1] < a [child]
if(a[par]<a[child])
{
//Exchange to meet the conditions of large top reactor
swap(a,par,child);
par=child;//Assign the subscript of the child node to the parent node
}
child=child*2+1;//Wrap compare the next
}
}
//Function to initialize the large top heap
void BuildHeap(int *a,int n)
{
for(int i=n/2-1;i>=0;i--)
{
MintoBig(a,i,n);
}
}
void HeapSort(int *a,int n)
{
BuildHeap(a,n);//Initialize the array to be queued and convert it to a large top heap
for(int i=n-1;i>0;i--)
{
swap(a,0,i);
MintoBig(a,0,i);
}
}
int main()
{
int n;
cin>>n;
for(int i=0;i<n;i++)
{
cin>>a[i];
}
cout<<"Before sorting:"<<endl;
for(int i=0;i<n;i++)
{
cout<<a[i]<<" ";
}
HeapSort(a,n);
cout<<"After sorting:"<<endl;
for(int i=0;i<n;i++)
{
cout<<a[i]<<" ";
}
return 0;
}Operation results:

6. Quick sort
Idea: quick sorting is an improvement of bubble sorting to improve its efficiency; The sequence to be arranged is divided into two independent parts by one-time sorting, in which the keywords of some records are smaller than those of the other part, and then the two parts can be sorted to achieve the order of the whole sequence;
Method 1:
Select the first element of each unordered partition as the pivot, define an element n = pivot subscript + 1, traverse the exchange of the unordered partition less than the pivot and the subscript n, N + + each time, and finally exchange the pivot and the last element less than the pivot;
The dynamic diagram is shown as follows:
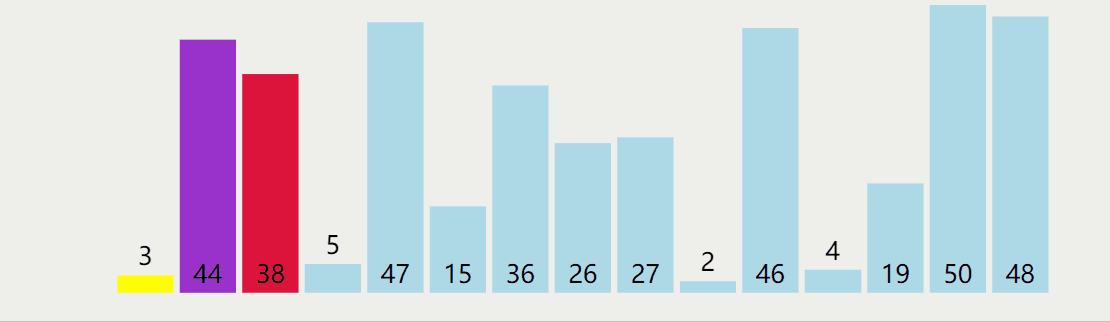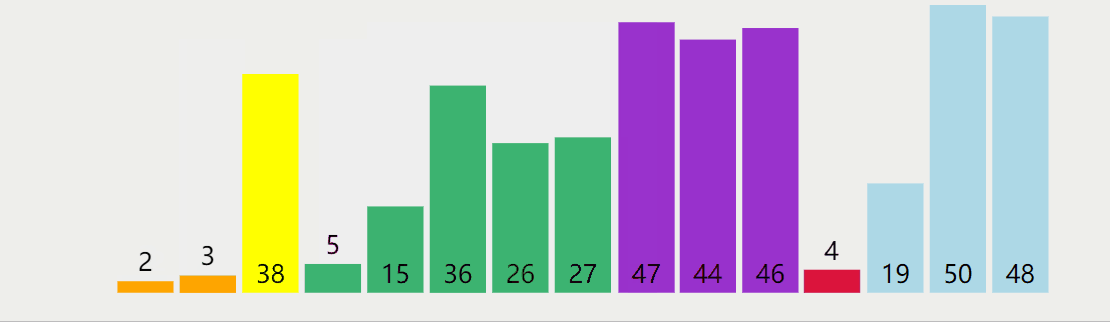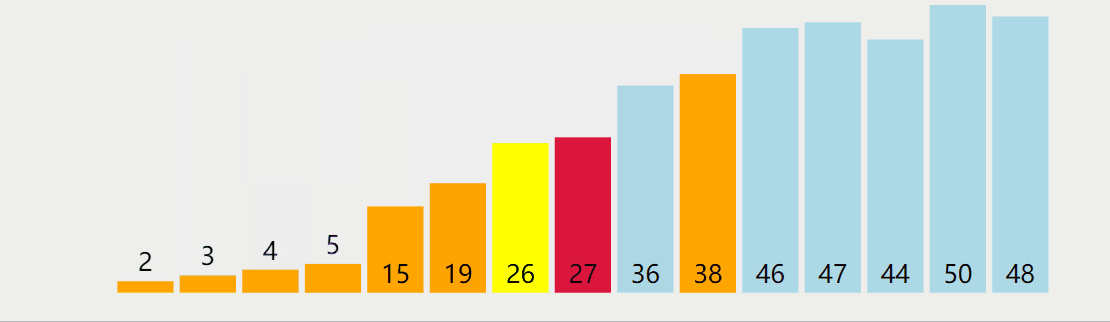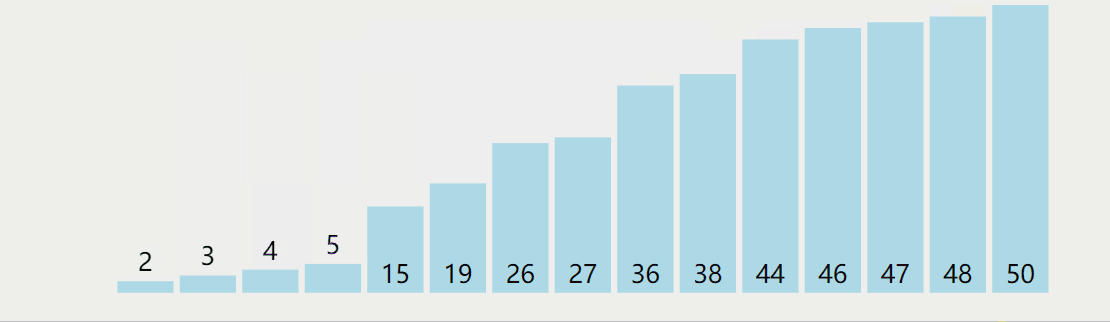
Method 2:
Select the first element of each unordered partition as the pivot, and use tem to record the value of the pivot. Use begin to represent the first element of the partition, and end to represent the last element of the partition. Start from the end element, look forward (end --) for elements smaller than the pivot, and assign the element to a[begin]; start from begin, look backward (begin + +) for elements larger than the pivot, And assigned to a[end]; When begin=end, the round ends and the pivot value is assigned to a[begin]. At this time, the sorted partition is divided into two parts, one of which is smaller than the other;
Note: the Peugeot at the end of each round of search is begin > = end;
Code display:
#include<iostream>
using namespace std;
#define N 1000
int a[N]={0};
void QuckSort(int *a,int begin,int end)
{
if(begin>end)
return ;
int i=begin;
int j=end;
int tem = a[begin];
while(i<j)
{
while(i<j&&a[j]>=tem)
j--;
a[i]=a[j];
while(i<j&&a[i]<=tem)
i++;
a[j]=a[i];
}
a[i]=tem;
QuckSort(a,begin,i-1);
QuckSort(a,i+1,end);
}
int main()
{
int n;
cin>>n;
for(int i=0;i<n;i++)
{
cin>>a[i];
}
cout<<"Before sorting:"<<endl;
for(i=0;i<n;i++)
{
cout<<a[i]<<" ";
}
cout<<endl;
QuckSort(a,0,n-1);
cout<<"After sorting:"<<endl;
for(i=0;i<n;i++)
{
cout<<a[i]<<" ";
}
return 0;
}Code run result:
