1. Foreword
Binary Search, also known as Binary Search, is an efficient search method, which can complete the search within the logarithmic time complexity of data scale. Binary Search can be applied to arrays because arrays have the characteristics of random access and arrays are orderly. The mathematical idea of Binary Search is "reduce and cure" , the properties of the elements on both sides can be inferred from the characteristics of the intermediate elements currently seen, so as to reduce the scale of the problem.
Binary search is also a common problem in the interview. Although its idea is very simple, it is not easy to write a binary search algorithm. Therefore, I summarized the high-frequency dichotomous questions of recent interviews with large Internet companies. The data comes from CodeTop , the solution comes from my LeetCode high frequency interview questions In the column, 7 high-frequency dichotomous questions are explained in detail to help the interviewer prepare the dichotomous algorithm questions in the interview more pertinently.
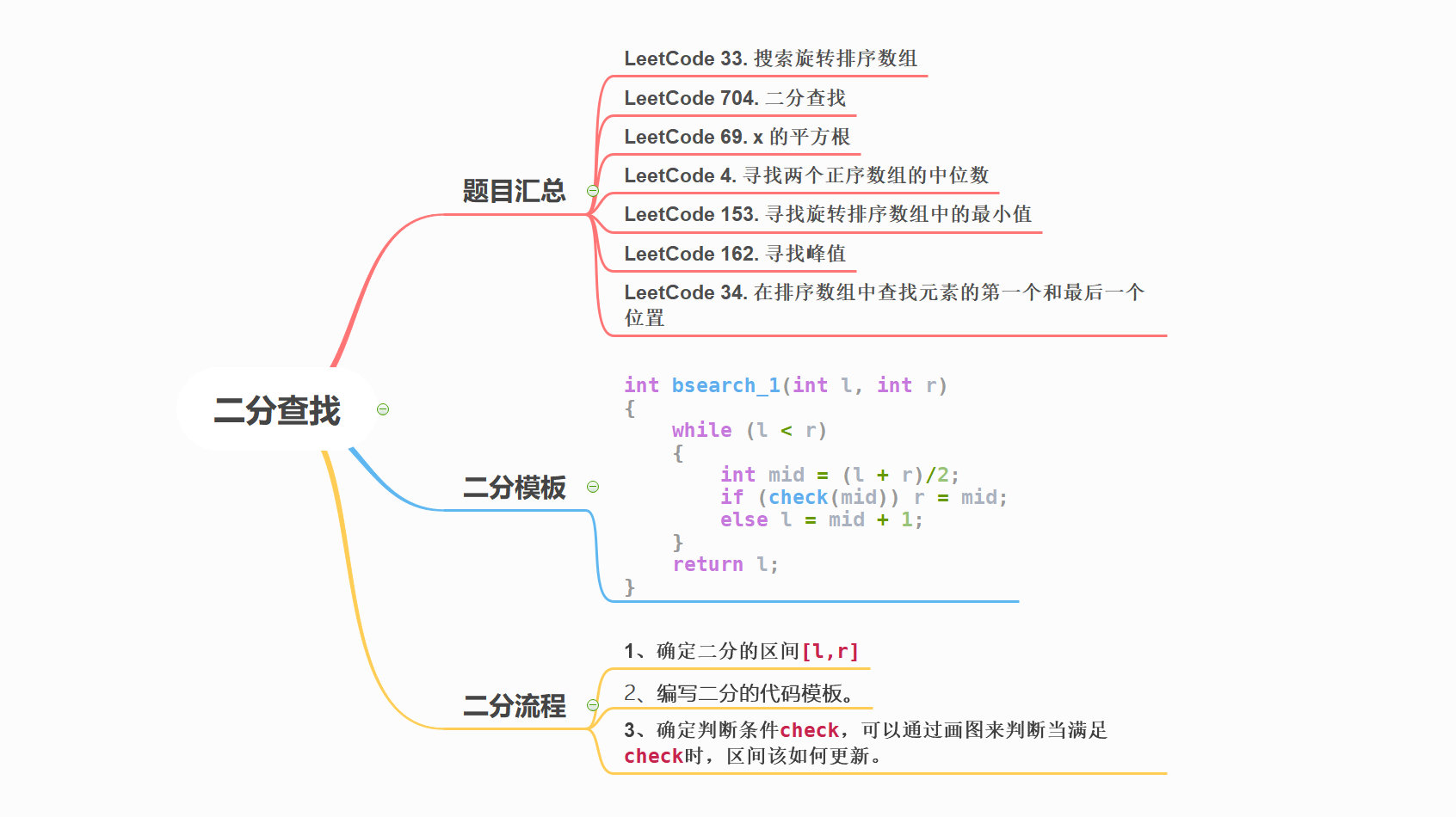
2. Topic summary
| subject | difficulty | Recent investigation time | frequency | Mastery degree |
|---|---|---|---|---|
| LeetCode 33. Search rotation sort array | secondary | 2021-08-19 | 65 | ⭐⭐⭐ |
| LeetCode 704. Binary search | easily | 2021-08-20 | 47 | ⭐⭐⭐ |
| LeetCode 69. Square root of X | easily | 2021-08-23 | 37 | ⭐⭐⭐ |
| LeetCode 4. Find the median of two positively ordered arrays | difficulty | 2021-08-21 | 27 | ⭐⭐⭐ |
| LeetCode 153. Find the smallest value in the rotation sort array | secondary | 2021-08-14 | 22 | ⭐⭐⭐ |
| LeetCode 162. Find peak | secondary | 2021-08-17 | 20 | ⭐⭐⭐ |
| LeetCode 34. Finds the first and last positions of elements in a sorted array | secondary | 2021-08-12 | 18 | ⭐⭐⭐ |
3. Bisection template
Version 1
When we divide the interval [l, r] into [l, mid] and [mid + 1, r], the update operation is r = mid or l = mid + 1. It is not necessary to add 1 when calculating mid.
C++/java code template:
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = (l + r)/2;
if (check(mid)) r = mid;
else l = mid + 1;
}
return l;
}
Version 2
When we divide the interval [l, r] into [l, mid - 1] and [mid, r], the update operation is r = mid - 1 or l = mid. at this time, in order to prevent dead circulation, add 1 when calculating mid.
C++/java code template:
int bsearch_2(int l, int r)
{
while (l < r)
{
int mid = ( l + r + 1 ) /2;
if (check(mid)) l = mid;
else r = mid - 1;
}
return l;
}
Code template link: https://www.acwing.com/blog/content/31/
4. Dichotomy process
- 1. Determine the interval [l,r] of dichotomy, which is generally L = 0, r = nums size() - 1.
- 2. Write a binary code template.
- 3. To determine the judgment condition check, you can draw a diagram to judge how to update the interval when the check is satisfied.
5. Detailed explanation of dichotomy high frequency problem
5.1,LeetCode 33. Search rotation sort array
Title:
The integer array nums is arranged in ascending order, and the values in the array are different from each other.
Before passing to the function, nums rotates on a previously unknown subscript k (0 < = k < nums. Length), so that the array becomes [nums [k], nums [K + 1],..., nums [n-1], nums [0], nums [1],..., nums [k-1]] (the subscript counts from 0). For example, after rotating at subscript 3, [0,1,2,4,5,6,7] may become [4,5,6,7,0,1,2].
Give you the rotated array num and an integer target. If the target value target exists in num, return its subscript, otherwise return - 1.
Example 1:
Input: nums = [4,5,6,7,0,1,2], target = 0 Output: 4
Example 2:
Input: nums = [4,5,6,7,0,1,2], target = 3 Output:-1
Example 3:
Input: nums = [1], target = 0 Output:-1
Tips:
- 1 <= nums.length <= 5000
- -10^4 <= nums[i] <= 10^4
- Each value in num is unique
- The title data ensures that nums rotates on a subscript unknown in advance
- -10^4 <= target <= 10^4
thinking
(two points) O ( l o g n ) O(logn) O(logn)
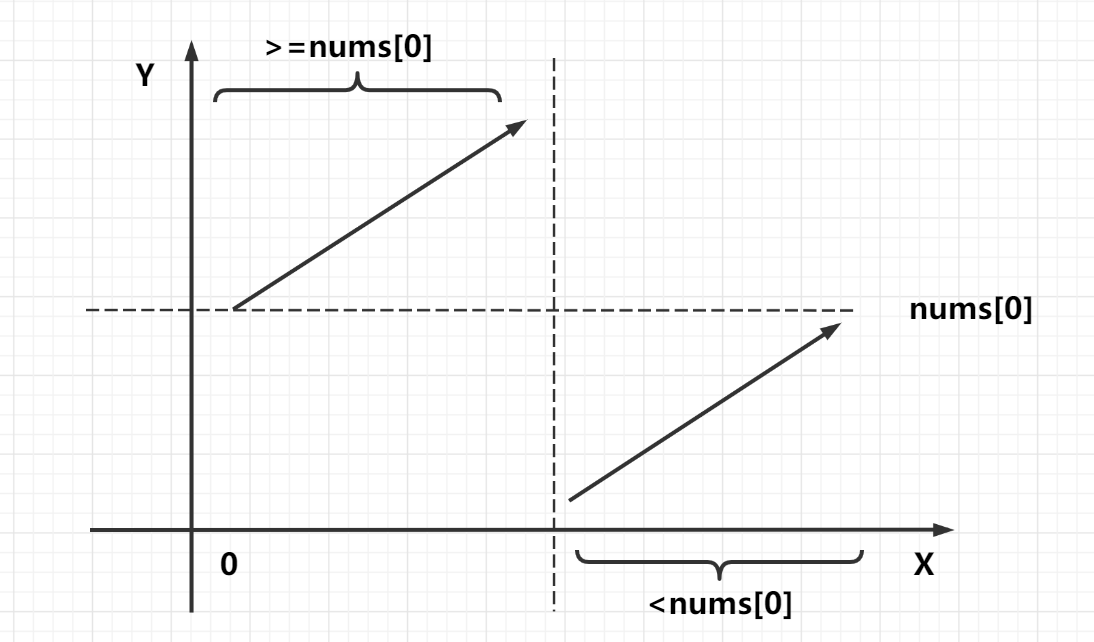
1. Find the rotation point first. The points on the left of the rotation point are larger than nums[0], and the points on the right are smaller than nums[0], so you can find the point with two points
-
When num [mid] > = num [0], look to the right area, l = mid.
-
When num [mid] < num [0], look to the left area, r = mid - 1.
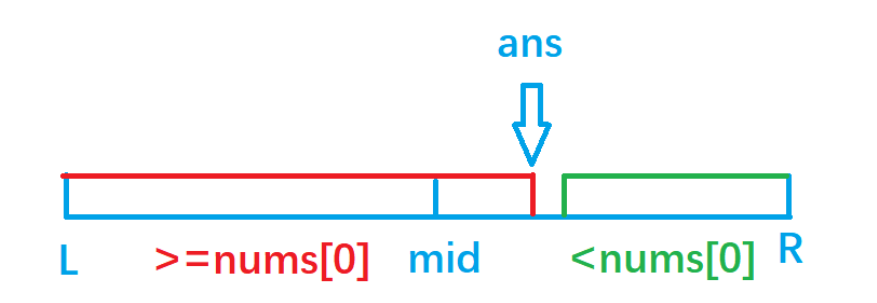
2. After finding the rotation point L, you can know that [0, L - 1] and [l, N - 1] are two ordered arrays, judge which ordered array the value of target is in, and determine the bisection interval [l,r]
3. In the interval [l,r], because the region is monotonic, the position of the value is found by dichotomy
-
When num [mid] > = target, look for the left area, r = mid.
-
When num [mid] < target, look to the right area, l = mid + 1.
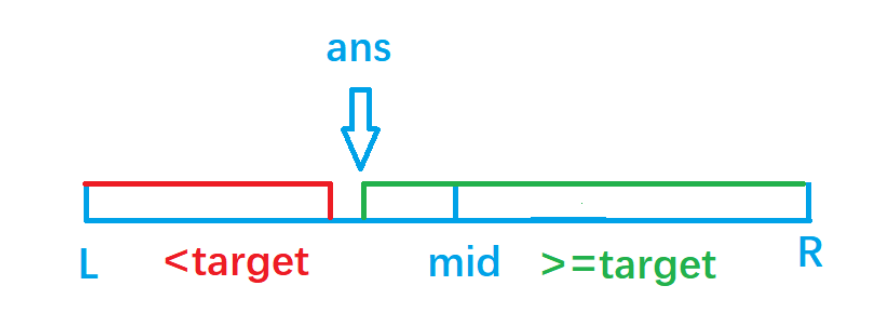
4. If the last element found is nums [R]= Target, indicating that the number does not exist, return - 1, otherwise return the value
c + + code
class Solution {
public:
int search(vector<int>& nums, int target) {
if(nums.empty()) return -1;
//First bisection turning point bisection > = rightmost of num [0]
int l = 0, r = nums.size() - 1;
while( l < r)
{
int mid = (l + r + 1)/2;
if(nums[mid] >= nums[0]) l = mid;
else r = mid - 1;
}
if(target >= nums[0]) l = 0; //target is in the left half area
else l = r + 1, r = nums.size() - 1; //target is in the right half area
while( l < r)
{
int mid = ( l + r)/2;
if( nums[mid] >= target) r = mid;
else l = mid + 1;
}
if(nums[r] == target) return r;//The end condition of the binary while cycle is l > = R, so l may be greater than R at the end of the cycle, which may lead to crossing the boundary. Basically, the binary problem takes r first and will not overturn.
return -1;
}
};
java code
class Solution {
public int search(int[] nums, int target) {
if(nums.length == 0) return -1;
//First bisection turning point bisection > = rightmost of num [0]
int l = 0, r = nums.length - 1;
while( l < r)
{
int mid = (l + r + 1)/2;
if(nums[mid] >= nums[0]) l = mid;
else r = mid - 1;
}
if(target >= nums[0]) l = 0; //target is in the left half area
else
{
l = r + 1;
r = nums.length - 1; //target is in the right half area
}
while( l < r)
{
int mid = ( l + r)/2;
if( nums[mid] >= target) r = mid;
else l = mid + 1;
}
if(nums[r] == target) return r;//The end condition of the binary while cycle is l > = R, so l may be greater than R at the end of the cycle, which may lead to crossing the boundary. Basically, the binary problem takes r first and will not overturn.
return -1;
}
}
5.2,LeetCode 704. Binary search
subject
Given an n-element ordered (ascending) integer array nums and a target value target, write a function to search the target in nums. If the target value exists, return the subscript, otherwise return - 1.
Example 1:
input: nums = [-1,0,3,5,9,12], target = 9 output: 4 explain: 9 Appear in nums Middle and subscript 4
Example 2:
input: nums = [-1,0,3,5,9,12], target = 2 output: -1 explain: 2 non-existent nums So return -1
Tips:
- You can assume that all elements in nums are not repeated.
- n will be between [1, 10000].
- Each element of num will be between [- 9999, 9999].
thinking
(two points) O ( l o g n ) O(logn) O(logn)
1. In the [l,r] interval, the num [i] array is monotonic, so the position of the value can be found through the leftmost boundary of bisection > = target
- When num [mid] > = target, look for the left area, r = mid
- When num [mid] < target, look to the right area, l = mid + 1
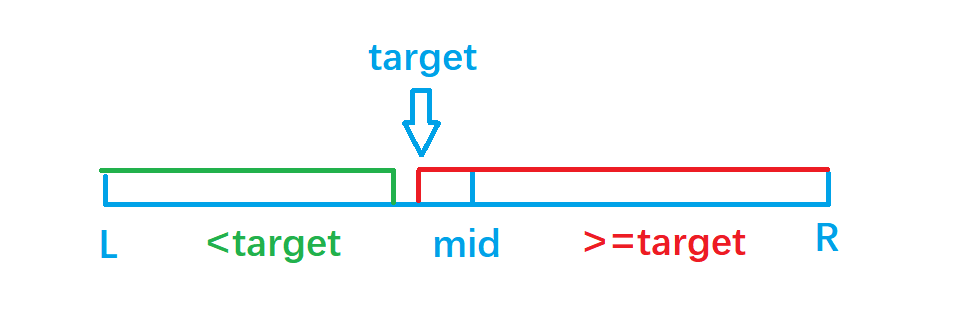
2. If the last element found is nums [r]= Target, indicating that the number does not exist, return - 1, otherwise return the value r
c + + code
class Solution {
public:
int search(vector<int>& nums, int target) {
if(!nums.size()) return -1;
int l = 0, r =nums.size() - 1;
while(l < r) //Leftmost boundary of bisection > = x
{
int mid = (l + r) / 2;
if(nums[mid] >= target) r = mid;
else l = mid + 1;
}
if(nums[r] == target) return r;
else return -1;
}
};
java code
class Solution {
public int search(int[] nums, int target) {
if(nums.length == 0) return -1;
int l = 0, r =nums.length- 1;
while(l < r) //Leftmost boundary of bisection > = x
{
int mid = (l + r) / 2;
if(nums[mid] >= target) r = mid;
else l = mid + 1;
}
if(nums[r] == target) return r;
else return -1;
}
}
5.3,LeetCode 69. Square root of X
subject
Implement the int sqrt(int x) function.
Calculates and returns the square root of X, where x is a nonnegative integer.
Since the return type is an integer, only the integer part of the result will be retained, and the decimal part will be rounded off.
Example 1:
input: 4 output: 2
Example 2:
input: 8 output: 2
explain:
- The square root of 8 is 2.82842,
- Since the return type is an integer, the decimal part will be rounded off.
thinking
(two points) O ( l o g x ) O(logx) O(logx)
We split the biggest one in two y 2 < = x y^2 <= x Y2 < = x, then y is the answer
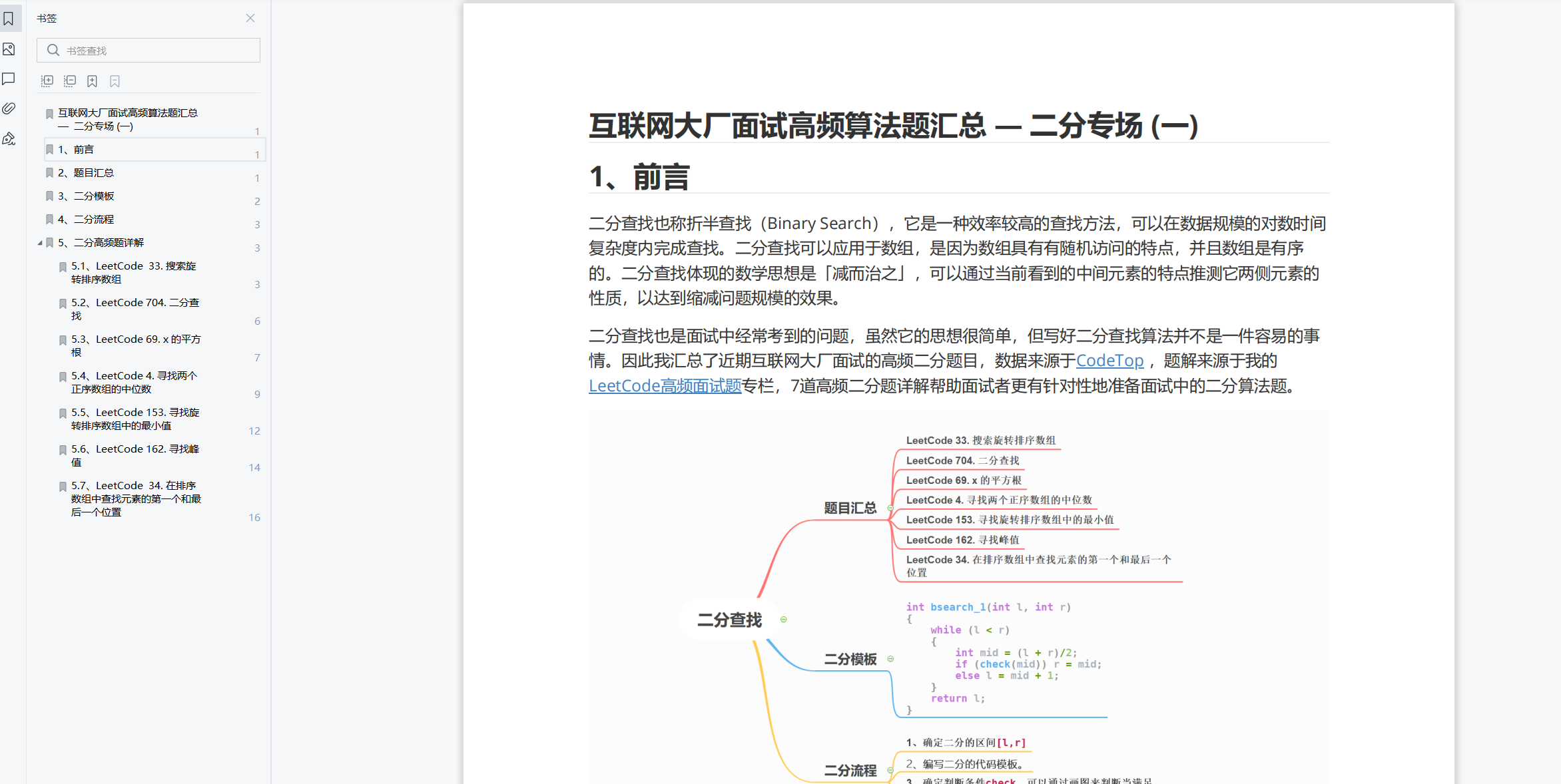
process
- 1. Let's start with l = 0, r = x and let mid = (l + r + 1)/2
- 2. If mid * mid < = x, look to the right, i.e. l = mid, otherwise look to the left, i.e. r = mid - 1.
Graphic process
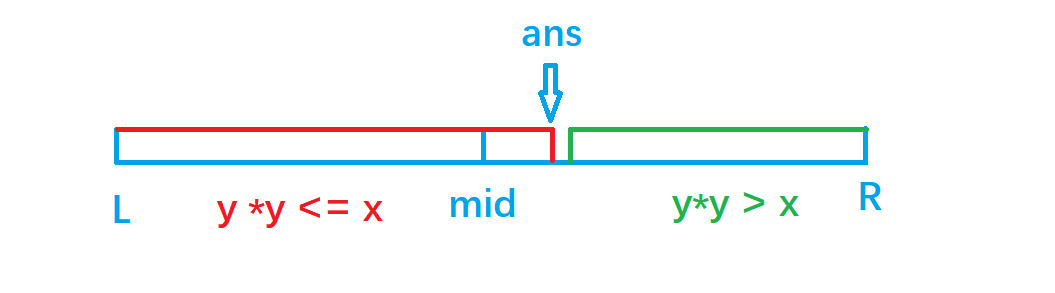
Time complexity O ( l o g x ) O(logx) O(logx)
Attention
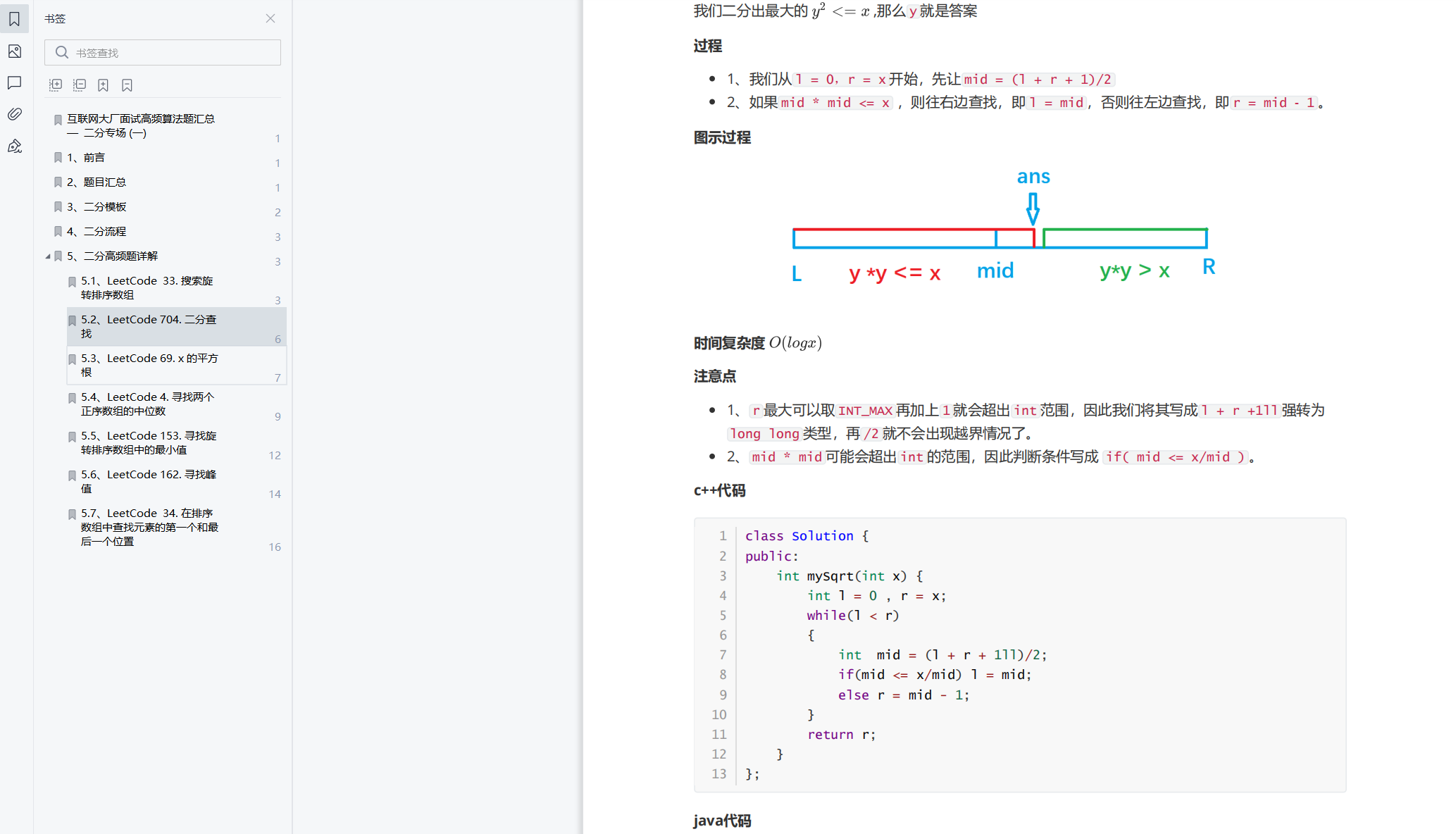
- 1. r max. INT_MAX plus 1 will exceed the int range, so we write it as l + r +1ll, and strongly convert it to long long, and then / 2 will not cross the boundary.
- 2. mid * mid may exceed the range of int, so the judgment condition is written as if (mid < = x / mid).
c + + code
class Solution {
public:
int mySqrt(int x) {
int l = 0 , r = x;
while(l < r)
{
int mid = (l + r + 1ll)/2;
if(mid <= x/mid) l = mid;
else r = mid - 1;
}
return r;
}
};
java code
class Solution {
public int mySqrt(int x) {
int l = 0, r = x;
while(l < r)
{
int mid = (int)(l + r + 1L >> 1);
if(mid <= x / mid) l = mid;
else r = mid - 1;
}
return l;
}
}
5.4,LeetCode 4. Find the median of two positively ordered arrays
subject
Give two positive ordered (from small to large) arrays nums1 and nums2 with sizes m and n respectively. Please find and return the median of these two positive ordered arrays.
Example 1:
Input: nums1 = [1,3], nums2 = [2] Output: 2.00000 Explanation: merge arrays = [1,2,3] ，Median 2
Example 2:
Input: nums1 = [1,2], nums2 = [3,4] Output: 2.50000 Explanation: merge arrays = [1,2,3,4] ，median (2 + 3) / 2 = 2.5
Example 3:
Input: nums1 = [0,0], nums2 = [0,0] Output: 0.00000
Example 4:
Input: nums1 = [], nums2 = [1] Output: 1.00000
Example 5:
Input: nums1 = [2], nums2 = [] Output: 2.00000
Tips:
- nums1.length == m
- nums2.length == n
- 0 <= m <= 1000
- 0 <= n <= 1000
- 1 <= m + n <= 2000
- -106 <= nums1[i], nums2[i] <= 106
Advanced: can you design an algorithm with time complexity O(log (m+n)) to solve this problem?
thinking
(recursion, dichotomy) O ( l o g ( n + m ) ) O(log(n+m)) O(log(n+m))
Finding the median of two positive arrays is equivalent to finding the k-th decimal in two positive arrays. If the sizes of the two arrays are n and m respectively, then the k = (n + m)/2 decimal is the median we require.
How to find the k-th smallest element?
The process is as follows:
1. Considering the general situation, we take the first k/2 elements in nums1 and nums2 arrays respectively
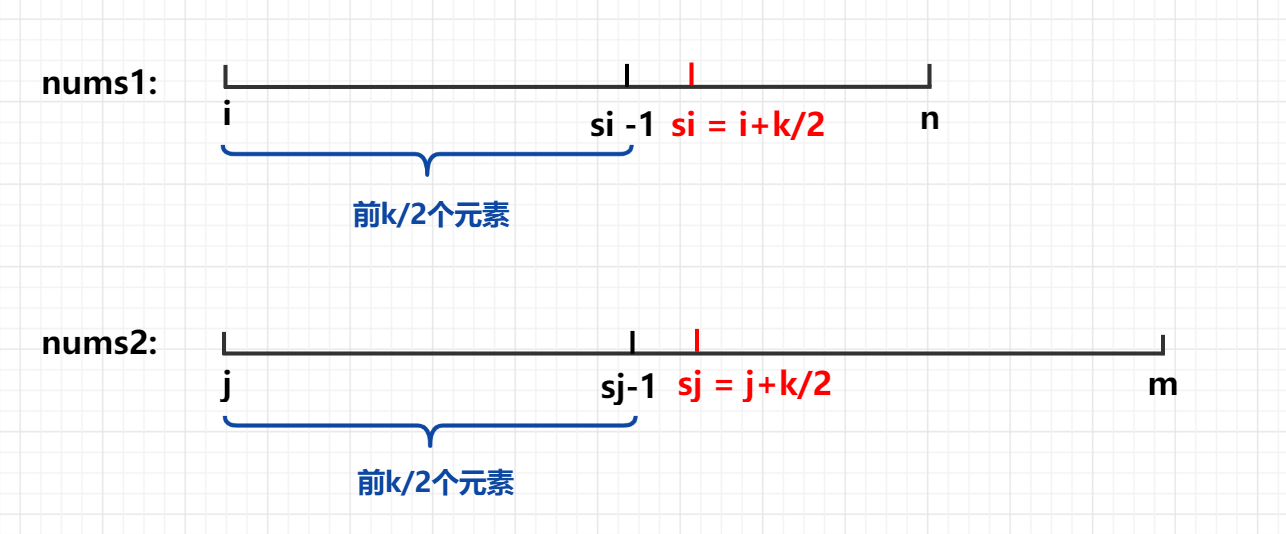
or_FFFFFF,t_70,g_se,x_16#pic_center)
By default, the effective length of nums1 array is smaller than that of nums2 array. The effective length of nums1 array starts from i, and the effective length of nums2 array starts from j, where [i,si - 1] is the first k / 2 elements of nums1 array and [j, sj - 1] is the first k / 2 elements of nums2 array.
2. Next, let's compare the sizes of nums1[si - 1] and nums2[sj - 1].
- If nums1 [Si - 1] > nums2 [SJ - 1], there are too many elements in nums1 and too few elements in nums2. Therefore, the first k/2 elements in nums2 must be less than or equal to the k-th decimal, that is, the elements in nums2[j,sj-1]. We can discard these elements and find the element with the smallest K - k/2 in the remaining interval, that is, the smallest K must be in [i,n] and [sj,m].
- If nums1 [Si - 1] < = nums2 [SJ - 1], similarly, it can be explained that the first k/2 elements in nums2 must be less than or equal to the k-th decimal, that is, the elements in nums1[i,si-1]. We can discard these elements and find the element with the smallest K - k/2 in the remaining interval, that is, the smallest K must be in [si,n] and [j,m].
3. Recursive process 2 can reduce the scale of the problem by half each time, and the last remaining number is the k-th decimal we want to find.
Recursive boundary:
- When nums1 array is empty, we directly return the k-th decimal of nums2 array.
- When k == 1 and both arrays are not empty, we return the minimum value of the first element of the two arrays, that is, min(nums1[i], nums2[j]).
Parity analysis:
-
When the sum total of the number of two array elements is an even number, find the smallest left of total / 2 and the smallest right of total / 2 + 1, and the result is (left + right / 2.0).
-
When total is an odd number, find the smallest total / 2 + 1, which is the result.
Time complexity analysis: k = ( m + n ) / 2 k=(m+n)/2 k=(m+n)/2, and each recursion k k The scale of k is reduced by half, so the time complexity is O ( l o g ( m + n ) ) O(log(m+n)) O(log(m+n)).
This problem is a dichotomous problem, but it will be easier to understand using recursive solution. Each recursion k k The scale of k is reduced by half, which is also the embodiment of the idea of dichotomy.
c + + code
class Solution {
public:
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int tot = nums1.size() + nums2.size();
if (tot % 2 == 0) {
int left = find(nums1, 0, nums2, 0, tot / 2);
int right = find(nums1, 0, nums2, 0, tot / 2 + 1);
return (left + right) / 2.0;
} else {
return find(nums1, 0, nums2, 0, tot / 2 + 1);
}
}
int find(vector<int>& nums1, int i, vector<int>& nums2, int j, int k) {
if (nums1.size() - i > nums2.size() - j) return find(nums2, j, nums1, i, k);
if (k == 1) {
if (nums1.size() == i) return nums2[j];
else return min(nums1[i], nums2[j]);
}
if (nums1.size() == i) return nums2[j + k - 1];
int si = min((int)nums1.size(), i + k / 2), sj = j + k - k / 2;
if (nums1[si - 1] > nums2[sj - 1])
return find(nums1, i, nums2, sj, k - (sj - j));
else
return find(nums1, si, nums2, j, k - (si - i));
}
};
java code
class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
int total = nums1.length + nums2.length;
if(total % 2 == 0)
{
int left = f(nums1,0,nums2,0,total / 2);
int right = f(nums1,0,nums2,0,total / 2 + 1);
return (left + right) / 2.0;
}
else return f(nums1,0,nums2,0,total / 2 + 1);
}
static int f(int[] nums1,int i,int[] nums2,int j,int k)
{
//By default, the first one is small
if(nums1.length - i > nums2.length - j) return f(nums2,j,nums1,i,k);
//When the first array has run out
if(nums1.length == i) return nums2[j + k - 1];
//When taking the first element
if(k == 1) return Math.min(nums1[i],nums2[j]);
int si = Math.min(nums1.length,i + k / 2),sj = j + k - k / 2;
if(nums1[si - 1] > nums2[sj - 1])
{
return f(nums1,i,nums2,sj,k - (sj - j));
}
else
{
return f(nums1,si,nums2,j,k - (si - i));
}
}
}
5.5,LeetCode 153. Find the smallest value in the rotation sort array
subject
An array of length n is known, which is arranged in ascending order in advance. After 1 to n rotations, the input array is obtained. For example, the original array num = [0,1,2,4,5,6,7] may be obtained after changing:
- If you rotate 4 times, you can get [4,5,6,7,0,1,2]
- If you rotate 7 times, you can get [0,1,2,4,5,6,7]
Note that arrays [a [0], a [1], a [2], The result of a [n-1]] rotation is array [a [n-1], a [0], a [1], a [2], a[n-2]] .
Give you an array nums with different element values. It was originally an array arranged in ascending order and rotated many times according to the above situation. Please find and return the smallest element in the array.
Example 1:
Input: nums = [3,4,5,1,2] Output: 1 Explanation: the original array is [1,2,3,4,5] ，Rotate 3 times to get the input array.
Example 2:
Input: nums = [4,5,6,7,0,1,2] Output: 0 Explanation: the original array is [0,1,2,4,5,6,7] ，Rotate 4 times to get the input array.
Example 3:
Input: nums = [11,13,15,17] Output: 11 Explanation: the original array is [11,13,15,17] ，Rotate 4 times to get the input array.
Tips:
- n == nums.length
- 1 <= n <= 5000
- -5000 <= nums[i] <= 5000
- All integers in nums are different from each other
- Num was originally an array sorted in ascending order and rotated 1 to n times
thinking
(two points) O ( l o g n ) O(logn) O(logn)
For the convenience of analysis, we first draw the numbers in the array in the two-dimensional coordinate system. The abscissa represents the array subscript and the ordinate represents the array value, as shown below:
We find that the number on the left of the vertical dotted line is satisfied, while the number on the right of the vertical dotted line is satisfied, and the dividing point is the minimum value of the whole array. Array has dichotomy, so we can dichotomy the position of the minimum value.
The process is as follows:
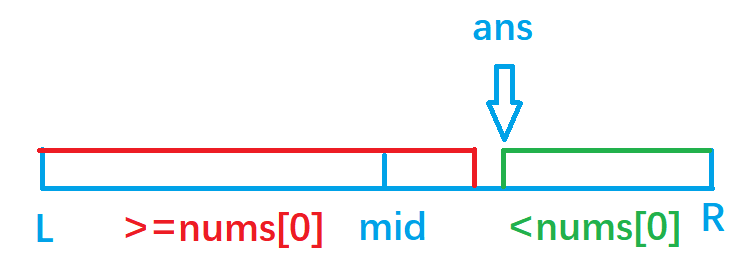
- 1. In the [l,r] interval, l = 0, r = nums Size () - 1, let's go to the leftmost boundary of bisection < num [0].
- 2. When num [mid] < num [0], look to the left area, r = mid..
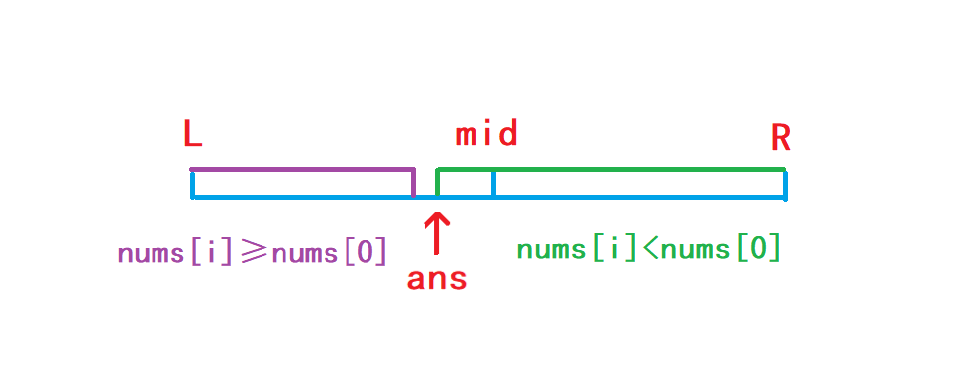
- 3. When num [mid] > = num [0], look to the right area, l = mid + 1.
- 4. When there is only one number left, it is the position of the minimum value.
Details:
- When the array is completely monotonous, the first number nums[0] is the smallest, and we can return it directly.
Time complexity analysis: binary search, so the time complexity is O ( l o g n ) O(logn) O(logn) .
c + + code
class Solution {
public:
int findMin(vector<int>& nums) {
int l = 0, r = nums.size() - 1;
if(nums[r] > nums[l]) return nums[0]; //Ascending array, the array is completely monotonic, and the first number is the smallest
while(l < r)
{
int mid = (l + r)/2;
if(nums[mid] < nums[0]) r = mid;
else l = mid + 1;
}
return nums[r];
}
};
java code
class Solution {
public int findMin(int[] nums) {
int l = 0, r = nums.length - 1;
if(nums[r] > nums[l]) return nums[0]; //Ascending array, the array is completely monotonic, and the first number is the smallest
while(l < r)
{
int mid = (l + r)/2;
if(nums[mid] < nums[0]) r = mid;
else l = mid + 1;
}
return nums[r];
}
}
5.6,LeetCode 162. Find peak
subject
The peak element refers to the element whose value is greater than the left and right adjacent values.
Give you an input array nums, find the peak element and return its index. The array may contain multiple peaks. In this case, just return the location of any peak.
You can assume nums[-1] = nums[n] = - ∞.
Example 1:
Input: nums = [1,2,3,1] Output: 2 Explanation: 3 is the peak element, and your function should return its index 2.
Example 2:
Input: nums = [1,2,1,3,5,6,4]
Output: 1 or 5
Explanation: your function can return index 1, and its peak element is 2;
Or return index 5, whose peak element is 6.
Tips:
- 1 <= nums.length <= 1000
- -231 <= nums[i] <= 231 - 1
- For all valid I, there are nums [i]= nums[i + 1]
thinking
(two points) O ( l o g n ) O(logn) O(logn)
Both ends of the array nums[-1] = nums[n] = - ∞ are negative infinity. Therefore, whether the array is monotonically increasing, monotonically decreasing, or undulating, the array must contain a peak. As shown in the figure below:
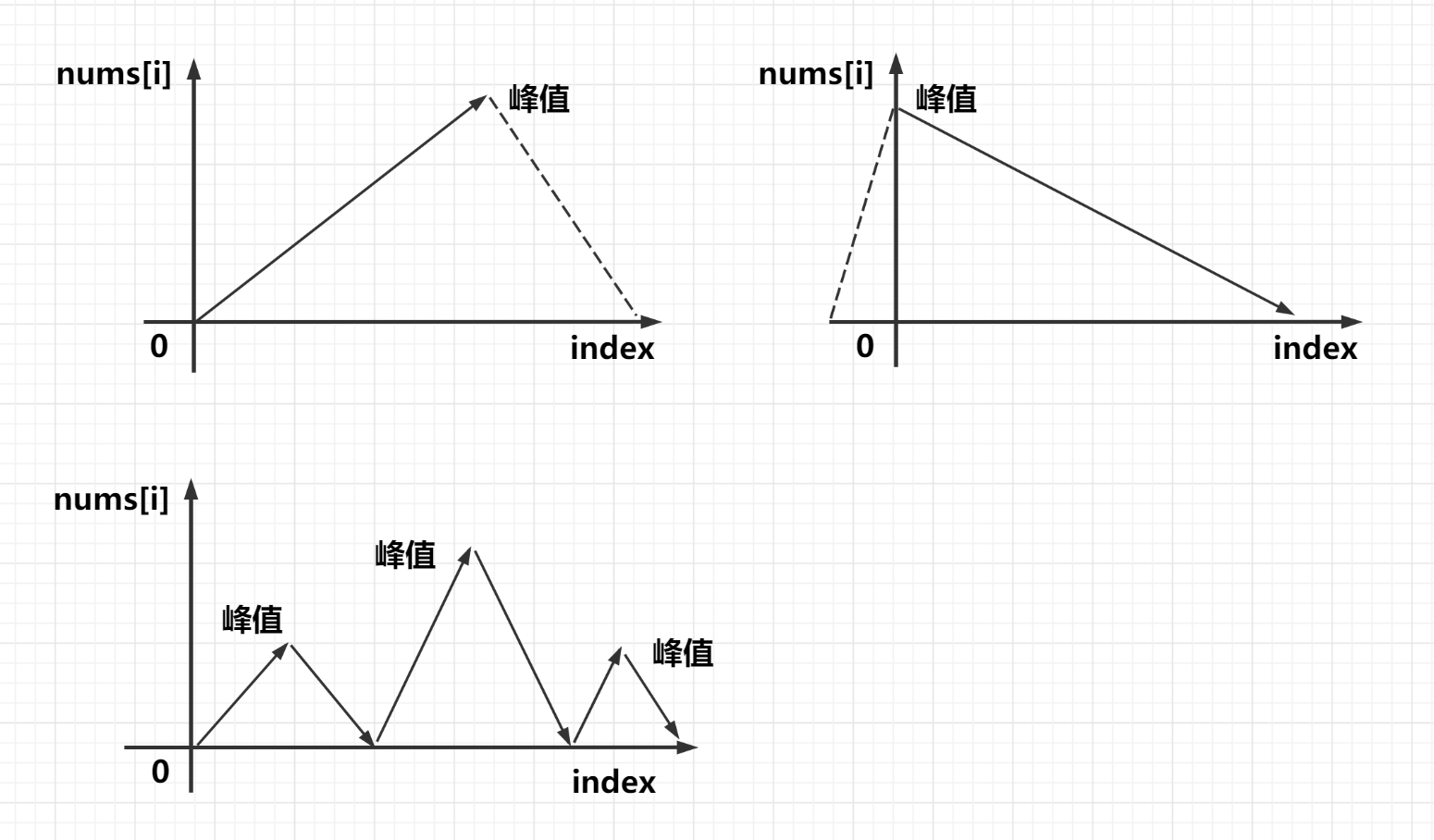
Because there is more than one peak in the array, we can find any one. The title also tells us that there are nums [i] for all valid I= Nums [i + 1], that is, any two adjacent numbers in the array are not equal.
We use dichotomy to find the mid point of the interval each time, compare the size relationship between num [mid] and num [mid + 1] to infer which interval must have a peak, and then take the interval with a peak. In this way, the range of the interval is continuously reduced, and the last number left in the interval is the answer.
The process is as follows:
- 1. Boundary of dichotomy, l = 0, r = nums size() - 1.
- 2. If num [mid] > num [mid + 1], there must be a peak in the interval [l,mid]. Because if [l,mid] decreases monotonically, then num [l] is the peak, otherwise the first rising point is the peak.
- 3. If num [mid] < num [mid + 1], there must be a peak in the interval [mid+1,r]. Because if [mid+1,r] increases monotonically, then num [R] is the peak, otherwise the first point of decline is the peak.
Time complexity analysis: binary search, so the time complexity is O ( l o g n ) O(logn) O(logn).
c + + code
class Solution {
public:
int findPeakElement(vector<int>& nums) {
int l = 0, r = nums.size() - 1;
while( l < r)
{
int mid = ( l + r )/2;
if(nums[mid] > nums[mid + 1]) r = mid;
else l = mid + 1;
}
return r;
}
};
java code
class Solution {
public int findPeakElement(int[] nums) {
int l = 0, r = nums.length - 1;
while( l < r)
{
int mid = ( l + r )/2;
if(nums[mid] > nums[mid + 1]) r = mid;
else l = mid + 1;
}
return r;
}
}
5.7,LeetCode 34. Finds the first and last positions of elements in a sorted array
subject
Given an integer array nums arranged in ascending order and a target value target. Find the start and end positions of the given target value in the array.
If the target value target does not exist in the array, return [- 1, - 1].
Advanced:
- Can you design and implement an algorithm with time complexity of O(log n) to solve this problem?
Example 1:
Input: nums = [5,7,7,8,8,10], target = 8 Output:[3,4]
Example 2:
Input: nums = [5,7,7,8,8,10], target = 6 Output:[-1,-1]
Example 3:
Input: nums = [], target = 0 Output:[-1,-1]
Tips:
- 0 <= nums.length <= 105
- -109 <= nums[i] <= 109
- num is a non decreasing group
- -109 <= target <= 109
thinking
(two points) O ( l o g n ) O(logn) O(logn)
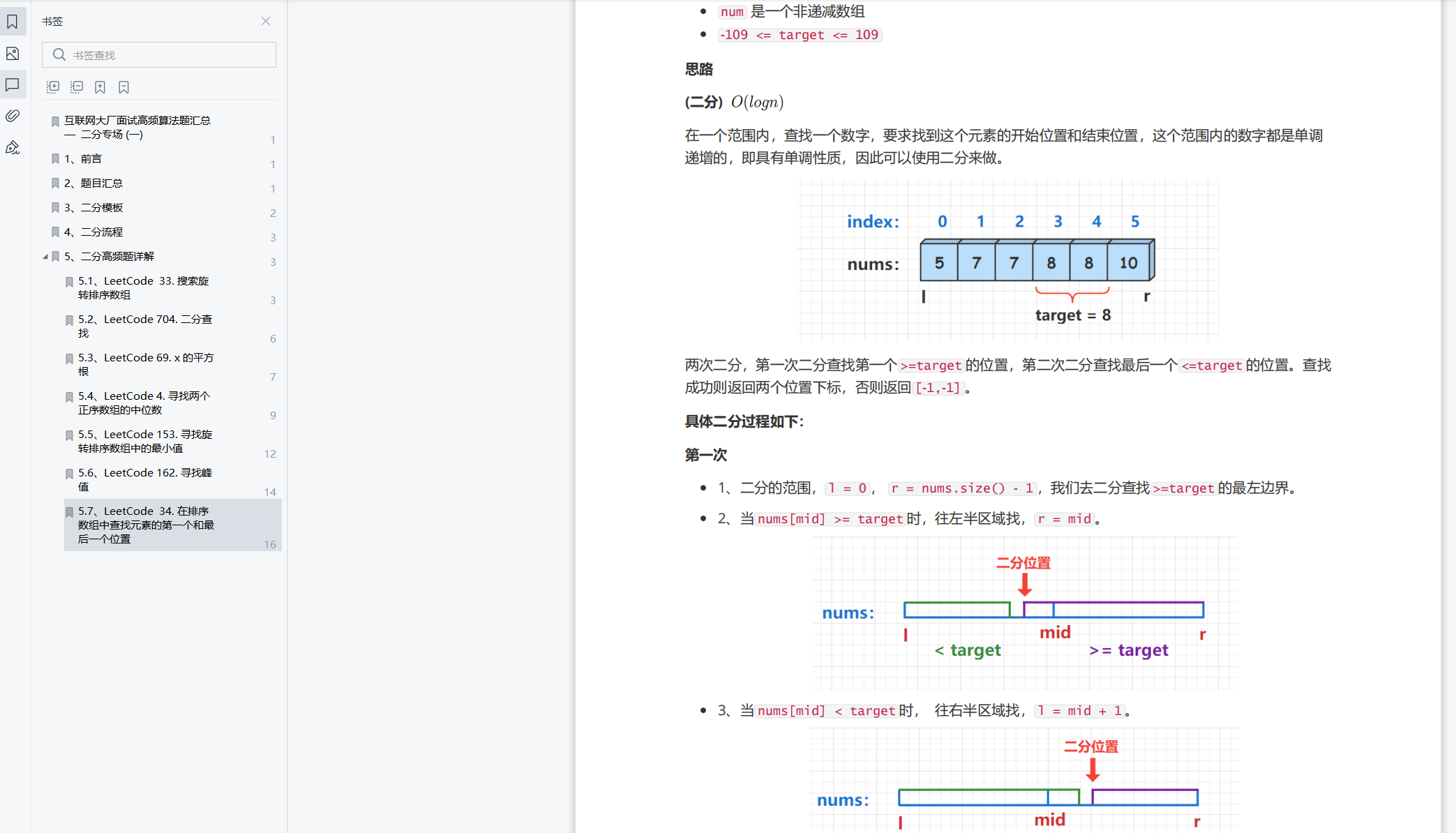
To find a number in a range, it is required to find the start position and end position of the element. The numbers in this range are monotonically increasing, that is, they have monotonic properties. Therefore, dichotomy can be used.
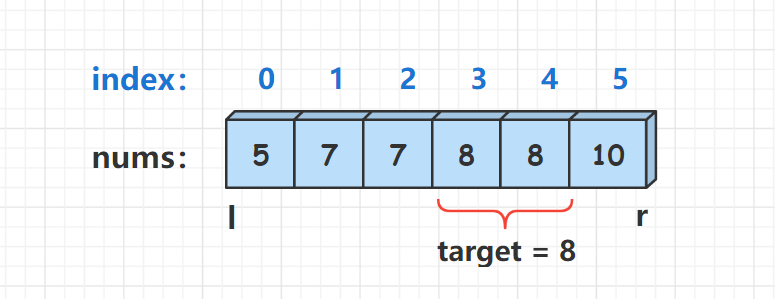Two bisections. The first bisection finds the position of the first ` > = target ', and the second bisection finds the position of the last ` < = target'. If the search is successful, two position subscripts will be returned, otherwise ` [- 1, - 1] `.
The specific two-part process is as follows:
for the first time
-
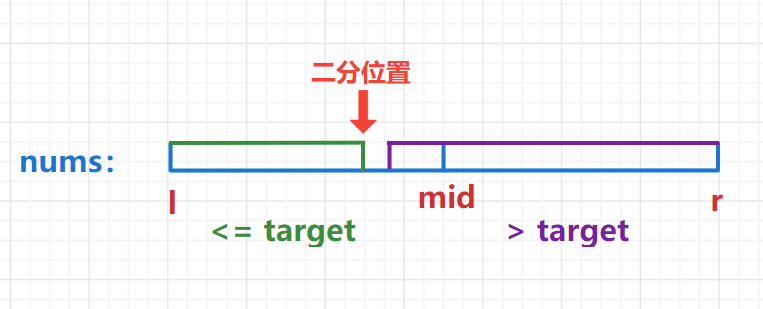
1. Dichotomous range, l = 0, r = nums Size () - 1, let's find the leftmost boundary of > = target.
-
2. When num [mid] > = target, look for the left half area, r = mid.
-
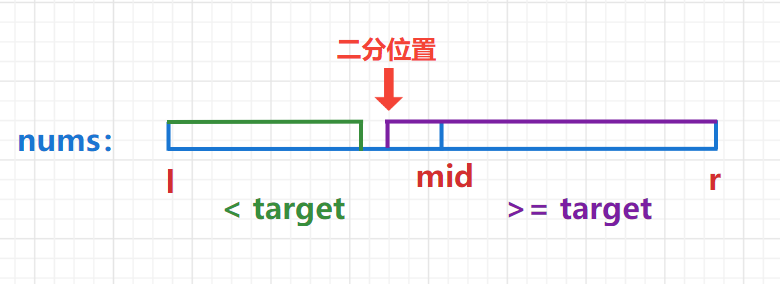
3. When num [mid] < target, look to the right half area, l = mid + 1.
-
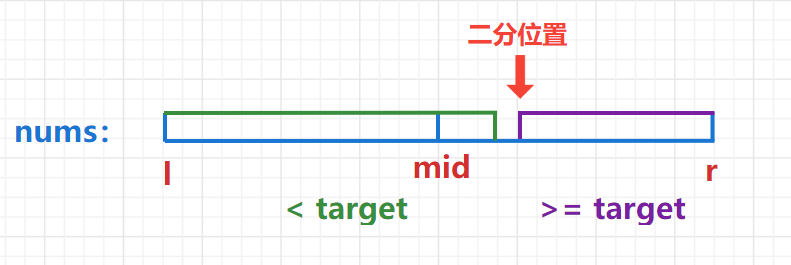
4. If nums [R]= Target, indicating that the target value target does not exist in the array, and [- 1, - 1] is returned. Otherwise, we find the position L of the first > = target.
The second time
-
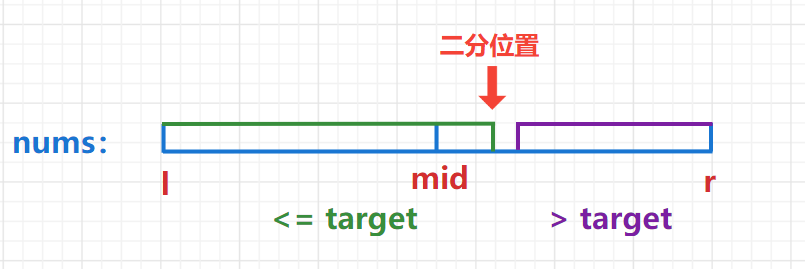
1. Dichotomous range, l = 0, r = nums Size () - 1, let's find the rightmost boundary of < = target.
-
2. When num [mid] < = target, look to the right half area, l = mid.
-
3. When num [mid] > target, look for the left half region, r = mid - 1.
-
4. Find the position r of the last < = target, and return the interval [L,R].
Time complexity analysis: the time complexity of two binary searches is O ( l o g n ) O(logn) O(logn).
c + + code
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
if(nums.empty()) return {-1,-1};
int l = 0, r = nums.size() - 1; //Dichotomous range
while( l < r) //Find the starting position of the element
{
int mid = (l + r )/2;
if(nums[mid] >= target) r = mid;
else l = mid + 1;
}
if( nums[r] != target) return {-1,-1};
int L = r;
l = 0, r = nums.size() - 1;
while( l < r) //Find the end position of the element
{
int mid = (l + r + 1)/2;
if(nums[mid] <= target ) l = mid;
else r = mid - 1;
}
return {L,r};
}
};
java code
class Solution {
public int[] searchRange(int[] nums, int target) {
if(nums.length == 0) return new int[]{-1,-1};
int l = 0, r = nums.length - 1; //Dichotomous range
while( l < r) //Find the starting position of the element
{
int mid = (l + r )/2;
if(nums[mid] >= target) r = mid;
else l = mid + 1;
}
if( nums[r] != target) return new int[]{-1,-1};
int L = r;
l = 0; r = nums.length - 1;
while( l < r) //Find the end position of the element
{
int mid = (l + r + 1)/2;
if(nums[mid] <= target ) l = mid;
else r = mid - 1;
}
return new int[]{L,r};
}
}
The notes have been summarized into PDF, and I can get private letters for free.
