First of all, let's take a look at the textbook (the textbook is very tall, it doesn't matter if you don't understand it, just continue to look down):

Then the textbook gives an example:

If you don't understand the above content, it's OK to look down from here~
In fact, this example can be understood sentence by sentence in combination with the above formula, but the problem-solving process may be relatively slow. In general, the key to matching is shift, and the key to shift is the value in next[i] in the above table.
next[j]=k, which means that the longest phase of the string before the character with subscript j is K. I think it's key to understand this. Next, I'll explain what is the prefix such as the longest appearance.
For example, a string is abcdab
The so-called prefix set can be understood as removing the last character, and then iterating back from the first character. The length of each iteration is increased by 1 and then stored in the set. On the contrary, the suffix set has the following results
Set of prefixes: {a,ab,abc,abcd,abcda}
Set of suffixes: {b,ab,dab,cdab,bcdab}
By comparing the two sets, we can see that the same part is ab and the length is 2, so the longest current suffix length is 2
Returning to the above example that is difficult to understand, the substring is abb. Let's calculate a case where j=4. The fifth letter corresponding to next[4], that is, a, we just said: next[i]=j, which means that the length of the longest phase of the string before the character with subscript I is J. The word "Qian" is very important, so what we need is the four letters before the fifth, that is, abab, so:
Set of prefixes: {a,ab,aba}
Set of suffixes: {b,ab,bab}
We can get that the equal part is ab and the length is 2, so the corresponding value of next[4] above is 2. It seems that it's not like to rush.
Well, the textbook compilers are not happy at this time. "Labor and capital worked hard to get you a formula, but you used this method to make opportunism". Then let's use the formula to calculate the next[4]:
Substring ABB

According to the formula, when j=4, the value of k can be 1,2,3. Let's test with a large value first (because it is the longest phase and other pre suffix, the large value can meet the conditions, regardless of the small one), and see if it meets the following conditions

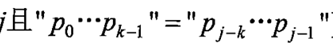
In the following analysis, P0 represents the first letter of the substring, P1 represents the second, and so on:
When k=3, the left side of the equation is P0P1P2=aba, the right side of the equation is P1P2P3=bab, the left is not equal to the right, and the equation is not tenable
When k=2, P0P1=ab on the left of the equation, P2P3=ab on the right of the equation, the left is equal to the right, and the equation holds, so next[4]=2

Relevant codes and improved codes (refer to other KMP algorithm articles):

typedef struct
{	
	char data[MaxSize];
	int length;			//String length
} SqString;
//Find next array
//SqString is the data structure of string
//typedef renames a structure variable. You can define a structure with SqString t.
void GetNext(SqString t,int next[])		//The next value is obtained from the mode string t
{
	int j,k;
	j=0;k=-1;
	next[0]=-1;//No string before the first character, give a value of - 1
	while (j<t.length-1) 
	//Because the maximum J in the next array is t.length-1, and the assignment of the next array in each step is after j + +
	//Therefore, j is t.length-2 when the while loop is passed for the last time
	{	
		if (k==-1 || t.data[j]==t.data[k]) 	//When k is - 1 or the compared characters are equal
		{	
			j++;k++;
			next[j]=k;
			//When the corresponding characters match, the s and t points move backward synchronously
			//Think about the meaning of this step in the process of finding the next array through the string "aaaaab"
			//printf("(1) j=%d,k=%d,next[%d]=%d\n",j,k,j,k);
       	}
       	else
		{
			k=next[k];
			**//We now know that the value of next[k] represents the length of the prefix such as the longest phase of the string before the character with subscript K
			//It also indicates the subscript of the character that should be traced back when there is a character mismatch
			//After this value is given to K, the while loop judgment is performed. At this time, t.data[k] refers to the character after the longest equal prefix**
			//Why go back here for comparison? Let's move on. In fact, the principle is similar to the KMP principle introduced above
			//printf("(2) k=%d\n",k);
		}
	}
}

int KMPIndex(SqString s,SqString t)  //KMP algorithm
{

	int next[MaxSize],i=0,j=0;
	GetNext(t,next);
	while (i<s.length && j<t.length) 
	{
		if (j==-1 || s.data[i]==t.data[j]) 
		{
			i++;j++;  			//i. J add 1 each
		}
		else j=next[j]; 		//i don't change, j goes back. Now you know why you let the substring go back like this
    }
    if (j>=t.length)
		return(i-t.length);  	//Returns the first character subscript of the matching pattern string
    else  
		return(-1);        		//Return mismatch flag
}

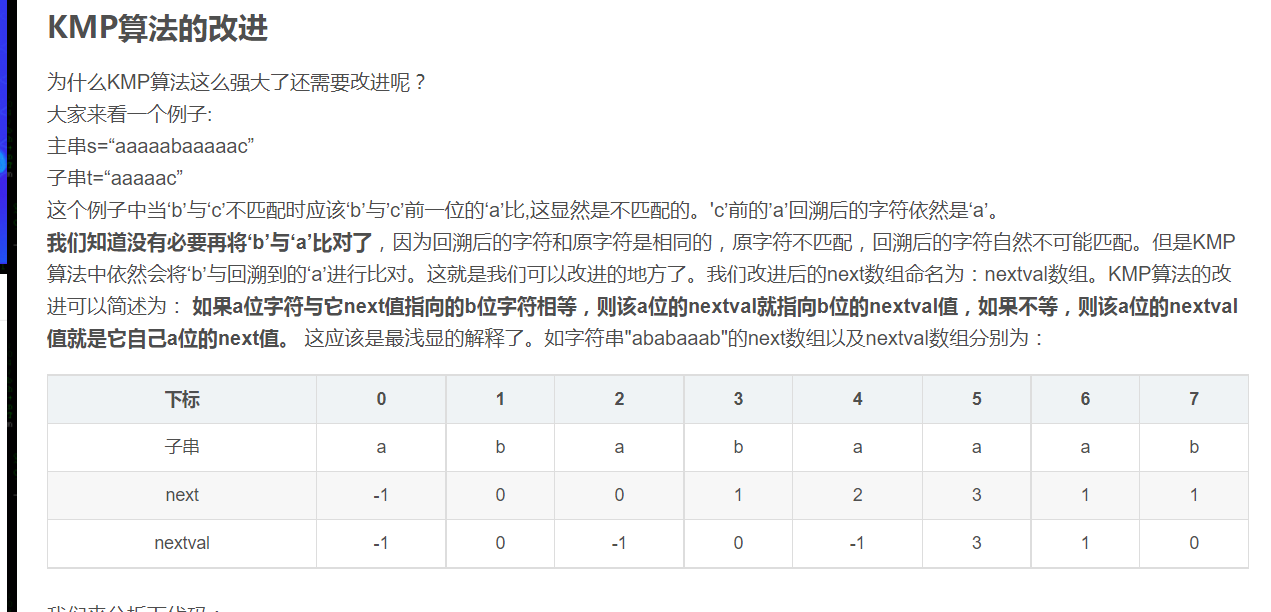
Optimize code

void GetNextval(SqString t,int nextval[])  
//The nextval value is obtained from the mode string t
{
	int j=0,k=-1;
	nextval[0]=-1;
   	while (j<t.length) 
	{
       	if (k==-1 || t.data[j]==t.data[k]) 
		{	
			j++;k++;
			if (t.data[j]!=t.data[k]) 
//t.data[k] here is the character that will be traced back due to the character mismatch at t.data[j]
//Why? If there is no if judgment, the code here is next[j]=k;
//next[j] is the character position that should be traced back when t.data[j] does not match
				nextval[j]=k;
           	else  
				nextval[j]=nextval[k];
//Is the meaning of this code ready to come out?
//At this time, the value of nextval[j] is the nextval value of the character that should be traced back when t.data[j] does not match
//Express in a more vulgar language: that is, when the characters do not match, trace back the corresponding character subscript after two layers
       	}
       	else  k=nextval[k];    	
	}

}


int KMPIndex1(SqString s,SqString t)    
//Modified KMP algorithm
//It's just that next is replaced by nextval
{
	int nextval[MaxSize],i=0,j=0;
	GetNextval(t,nextval);
	while (i<s.length && j<t.length) 
	{
		if (j==-1 || s.data[i]==t.data[j]) 
		{	
			i++;j++;	
		}
		else j=nextval[j];
	}
	if (j>=t.length)  
		return(i-t.length);
	else
		return(-1);
}