These three sorts have two-layer cycles, which is their superficial feature. I call the external cycle large cycle and the internal cycle small cycle. Their basic idea of algorithm is the same, that is, the sequence to be sorted is divided into disordered interval and ordered interval. Each large cycle can increase the ordered interval and reduce the corresponding disordered interval:

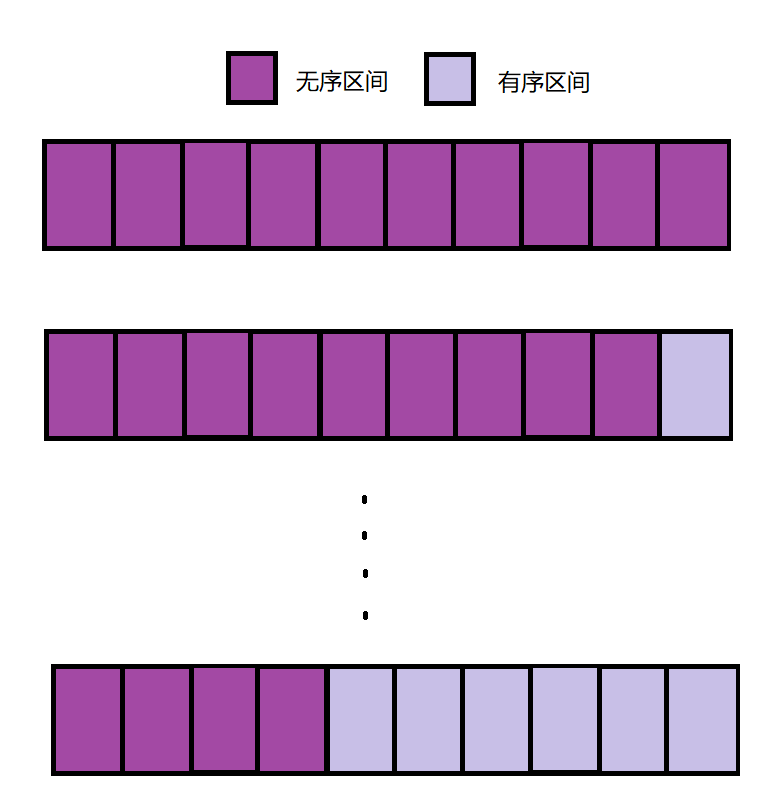
Let's talk about this algorithm that reduces the scale of the problem through the same operation every time. It is called reduction algorithm. Now we know their underlying ideas, and then discuss them separately for distinction.

Bubble sorting

The earliest sorting algorithm you come into contact with should be bubble sorting. His process is shown in the following figure: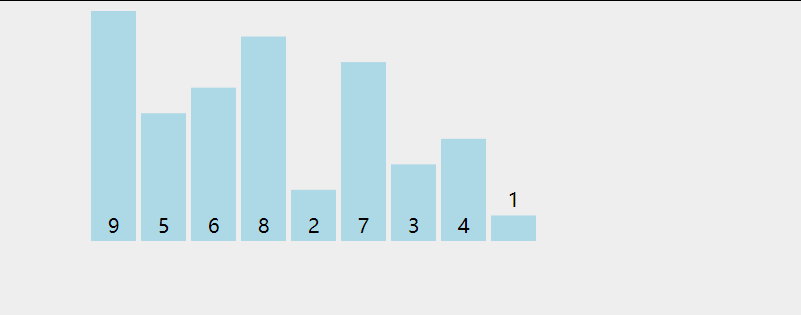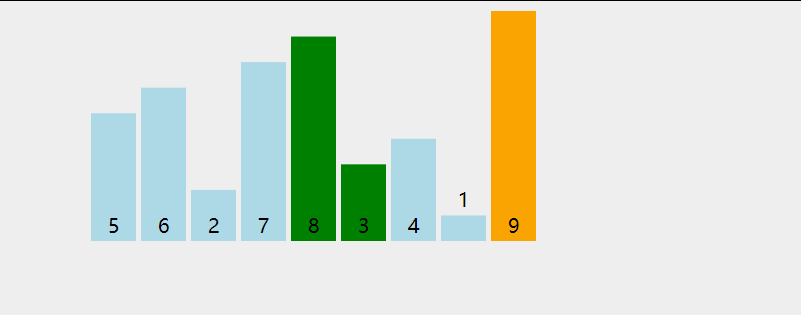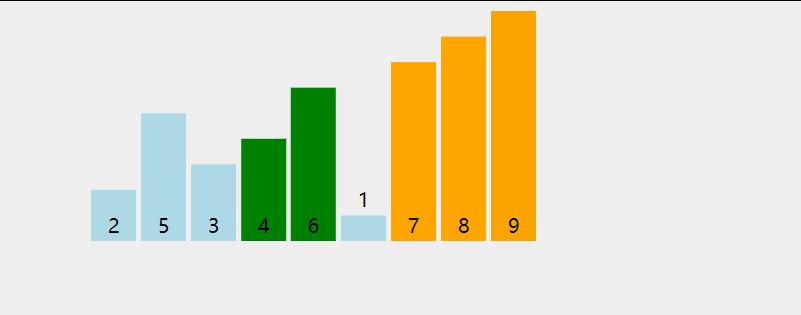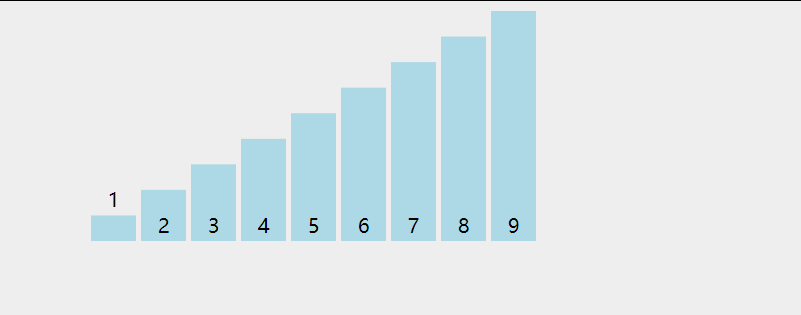

Take the ascending order in the figure as an example. Each small cycle starts from 0. The maximum number encountered in the traversal process pops up all the way to the ordered interval like bubbles. A large cycle increases the ordered interval by one. After the execution of the large cycle, all the intervals will be orderly. Here is its code:

import java.util.Arrays;

public class BubbleSort {
    //Ascending order
    public static void bubbleSort(int[] array){
        for (int i = 0; i < array.length - 1; i++){
            //Variables to optimize bubble sorting
            boolean judge = true;
            for (int j = 0; j < array.length - i - 1;  j++){
                //To decrease the order, change > to < instead
                if (array[j] > array[j + 1]){
                    int t = array[j];
                    array[j] = array[j + 1];
                    array[j + 1] = t;
                    judge = false;
                }
            }
            if (judge)
                return;
        }
    }

    public static void main(String[] args) {
        int[] array = { 1, 7, 6, 5, 2};
        bubbleSort(array);
        System.out.println(Arrays.toString(array));
    }
}

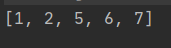
Operation results:

Select sort

Selective sorting is most similar to bubble sorting, but selective sorting is to select a maximum value for each large cycle, remember its subscript, and finally exchange with the last number of disordered interval to add one to the ordered interval in turn, while bubble sorting is changed during traversal.
Select sorting process:

As shown in the figure above, each time we traverse the unordered interval, we will select a maximum value, remember the subscript, and exchange the subscript with the last unordered interval after the traversal.
Code implementation:

public class SelectSort {
    /*
        Selective sorting is to select the largest (smallest) to be placed at the end of the unordered interval each time the sequence is traversed
    */

    //Ascending order
    public static void selectSort(int[] array){
        for (int i = 0; i < array.length; i++){
            int minVal = array[0];
            int minIdex = 0;
            for (int j = 1; j < array.length - i; j++){
                //To decrease the order, change > to < instead
                if (array[j] > minVal){
                    minIdex = j;
                    minVal = array[j];
                }
            }
            array[minIdex] = array[array.length - i - 1];
            array[array.length - i - 1] = minVal;
        }
    }
    public static void main(String[] args) {
        int[] array = { 1, 2, 6, 5, 7};
       selectSort(array);
        System.out.println(Arrays.toString(array));
    }
}

Operation results:

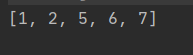
Insert sort

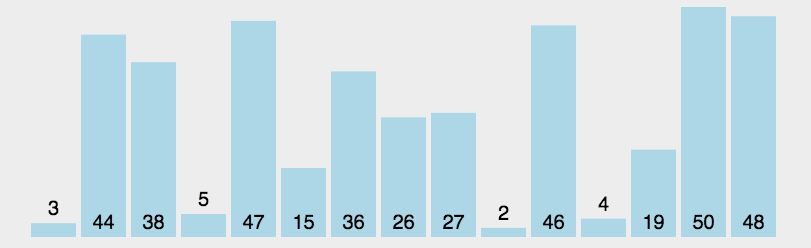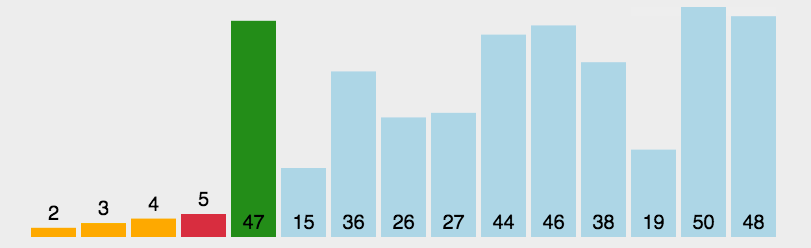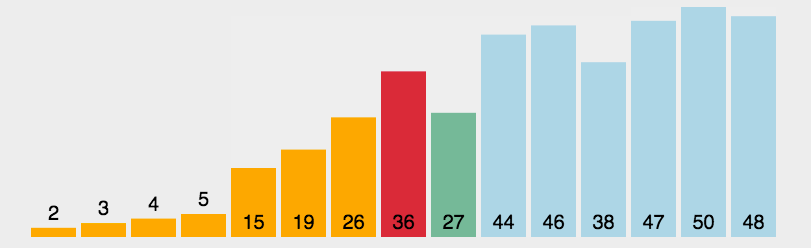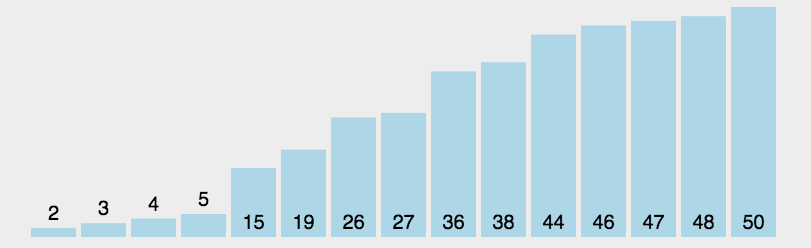
The insertion sort is slightly more complicated than the above two sorts. At the beginning, he regards the first element as an ordered interval, and then takes the first number of the unordered interval to compare it with the number of the ordered interval, find his own position, and then insert. The following figure is very clear:
The following is the code implementation:

//Ascending order
    public static void insertSort(int[] array){
        for (int i = 1; i < array.length; i++){
            int index = 0;
            int val = array[i];
            for (int j = i - 1; j >= 0; j--){
                //To decrease the order, change > to < instead
                if (val > array[j]){
                    index = j + 1;
                    break;
                }
                array[j + 1] = array[j];
            }
            array[index] = val;
        }
    }
    public static void main(String[] args) {
        int[] array = { 1, 5, 6, 7, 2 };
        insertSort(array);
        System.out.println(Arrays.toString(array));
    }
}

Operation results:

Although the above three sorts look very similar, they can be quickly distinguished according to the introduction, dynamic diagram and code.