1, Some concepts

1. Bipartite diagram

• It must not contain odd rings, but may contain rings with even length, not necessarily connected graphs
• Bipartite graph is a special model in graph theory. Let G=(V,E) be an undirected graph. If vertex v can be divided into two disjoint subsets (A,B), and the two vertices i and j associated with each edge (i, J) in the graph belong to these two different vertex sets (i in A,j in B), then graph G is called a bipartite graph. In short, if the midpoint of a graph can be divided into two groups and all edges cross the boundary of the group, it is a bipartite graph. To be exact, the vertices of a graph are divided into two disjoint subsets, so that each edge connects the vertices in the two sets respectively. If such a division exists, the graph is a bipartite graph, as shown in the following figure. All bipartite graphs are bipartite graphs:
  

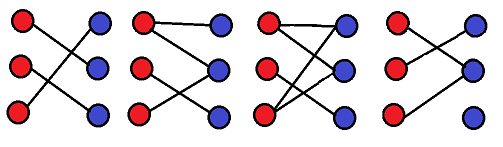
There is an important theorem about bipartite graph: G is a bipartite graph if and only if the length of each ring in G is even, which is not proved here.

2. Bipartite graph matching

• Matching of bipartite graph: given a bipartite graph G, in a subgraph m of G, if any two edges in the edge set {E} of M are not attached to the same vertex, M is called a matching.
• Maximum matching of bipartite graph: a group of matches with the largest number of edges in all matches is called the maximum matching of bipartite graph, and the number of edges is the maximum matching number.

Is it abstract to understand? It doesn't matter. Let me give an example: let's assume that the left side of the bipartite graph is full of boys and the right side is full of girls. The male and female students connected by lines are lovers. Chaotic male and female relations such as stepping on n boats are allowed. Then:

• Matching of bipartite graph: delete some edges of the bipartite graph so that the relationship between boys and girls does not step on n boats, that is, the new graph obtained after deleting edges is a match (single dogs are allowed)
• Maximum matching of bipartite graph: deleting some edges makes the maximum number of lovers reserved. We call this matching the maximum matching.

For example, in the above four figures, figure 1 is a maximum match of Figure 3.

2, Implementation steps of Hungarian algorithm

At the beginning of the story, as Cupid, you get the relationship diagram between four pairs of boys and girls

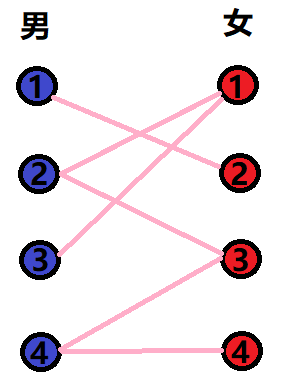
What a chaotic relationship

But it doesn't matter. We will turn into pure love soldiers to restore their chaotic relationship between men and women to normal! Get to work!

1. Situation 1 (you are my only)

First of all, we look at man 1 and find that man 1 is very pure and only likes woman 2, so let's help them. Determine their relationship.

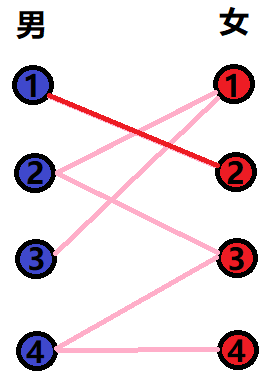
2. Situation 2 (you are all my wings)

Next, we looked at Man 2 and found that man 2 liked girls 1 and 3. Ask Man 2. He said: I'm sincere to these two girls. I can choose anyone!

You can choose anyone. Let's choose whatever you want and put male 2 and female 1 on the red line.

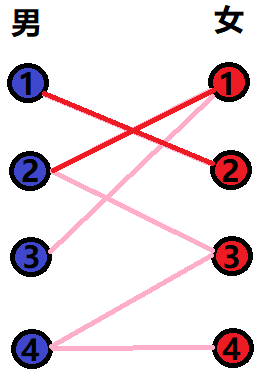
3. Situation 3 (I'll grab you)

OK, then let's look at Man 3. Man 3 says: I like woman 1 too! Obviously, I like her more! Why? Why is she with others! I can't accept it!

Well... It seems that our man 3 doesn't want to give up. Let's try to negotiate with man 2.

"Man 2, do you have a spare tire?"
"Yes, what's the matter?"
"Boyfriend 3 has a crush on your girlfriend. Why don't you stay with your spare tire and give your girlfriend to someone else?"
"Well... Well, remember to let him invite me to dinner" (the author strongly condemns the scum man like man 2!)

ok, then the matter will be solved satisfactorily. Congratulations.

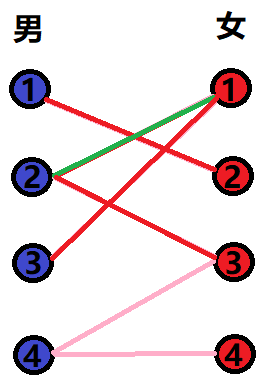
4. Situation 4 (the person I love already has a lover)

After solving the problems of Man 2 and Man 3, let's look at man 4.

Man 4 said: I like woman 3! I want to be with girl 3!
I looked. Isn't female 3 the new girlfriend of male 2? Well... I'll go and see man 2 again.

"What? Do you want me to change it? Brother, I don't have another spare tire. I refuse! If I have a spare tire, it's almost the same." (the author strongly condemns such a scum man as man 2!)

We had to look back and find man 4. Well, our negotiation failed. Female 3 is out of the game. Why don't you change your pursuit object and I'll fight for it for you?

Man 4 bowed his head and thought for a while, "I think, woman 4 is actually very cute."

ok, arrange! We looked and found that female 4 is still single. Let's help you.

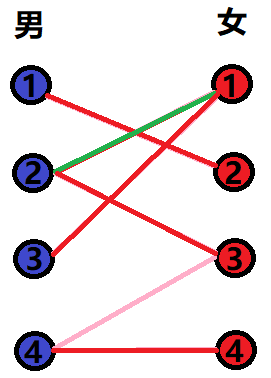
Finally, the maximum match we get is like this

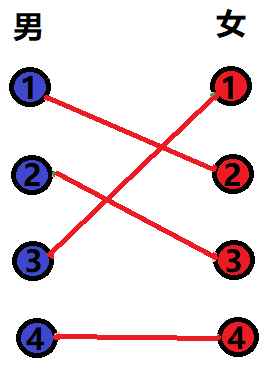
The relationship between men and women is normal, and pure love for the party looks satisfied~

• Summary: algorithm description:
  If the girl you're looking for already has a boyfriend,
  Just ask her boyfriend,
  Do you have a spare tire,
  Give me your girlfriend if you have a spare tire
  You don't have a spare tire, so I have to find my spare tire

What a real and practical algorithm~
The time complexity is O(nm), but in practice, the time is generally less than n*m.
What a good algorithm, even the time complexity is so elegant~

3, Code implementation of Hungarian algorithm

Example link: Maximum matching of Acwing bipartite graph
Hungarian algorithm board problem is a problem that must be mastered

Given a bipartite graph, the left half contains n1 Points (No. 1)∼n1)，The right half contains n2 Points (No. 1)∼n2)，Bipartite graph contains m Edge.

The data guarantees that neither end point of any edge can be in the same part.

Please find the maximum matching number of bipartite graph.

Bipartite graph matching: given a bipartite graph G，stay G A subgraph of M In, M Edge set of {E} If any two edges in are not attached to the same vertex, it is called M Is a match.

Maximum matching of bipartite graph: a group of matches with the largest number of edges in all matches is called the maximum matching of bipartite graph, and the number of edges is the maximum matching number.

Input format
 The first line contains three integers n1, n2 and m. 

next m Rows, each containing two integers u and v，Represents the point in the left half point set u And the point in the right half v There is an edge between.

Output format
 Output an integer representing the maximum matching number of bipartite graphs.

Data range
1≤n1,n2≤500,
1≤u≤n1,
1≤v≤n2,
1≤m≤1e5
 Input example:
2 2 4
1 1
1 2
2 1
2 2
 Output example:
2

Code implementation and analysis

//#pragma GCC optimize(2)
#include<iostream>
#include<iomanip>
#include<cstdio>
#include<string>
#include<algorithm>
#include<cmath>
#include<queue>
#include<vector>
#include<map>
#include<stack>
#include<set>
#include<bitset>
#include<ctime>
#include<cstring>
#include<list>
#define ll long long
#define ull unsigned long long
#define INF 0x3f3f3f3f
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
typedef  pair<int, int> PII;
const int N = 1e6 + 7;
int n1, n2, m;
int h[550], ne[N], e[N], id = 1;// Chained forward star map
bool st[N];//Prevent the situation of heavy edge from leading to a dead cycle, and prevent a boy from repeatedly asking a girl from leading to a dead cycle
int match[N];//Used to save the number of boys matched by girls

void add(int a, int b)
{
	e[id] = b, ne[id] = h[a], h[a] = id++;
}

int find(int x)  //Can boys x match girls
{
	for (int i = h[x]; i != -1; i = ne[i])  //Traverse all edges
	{
		int j = e[i];
		if (!st[j])  //Prevent dead circulation caused by heavy edges
		{
			st[j] = true;
			if (!match[j] || find(match[j]))  //If the girl doesn't have a boyfriend or her current boyfriend has a spare tire
			{
				match[j] = x;  //Then let her boyfriend change the spare tire, and then she becomes x's girlfriend
				return true;  //Match successful
			}
		}
	}
	return false;  //Matching failed
}


void solve()
{
	mem(h, -1);
	cin >> n1 >> n2 >> m;
	while (m--)
	{
		int a, b;
		cin >> a >> b;
		add(a, b);
	}
	int res = 0;
	for (int i = 1; i <= n1; i++)
	{
		mem(st, false);  //Reset
		if (find(i))  //Find me a girlfriend
			res++;
	}
	cout << res << endl;
}

int main()
{
	std::ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);
	solve();
	return 0;
}

Author: Avalon Demerzel, just like my blog. For more knowledge about graph theory and data structure, see the author's column graph theory and data structure