catalogue
Input sample 1 (the title comes with it)
Input example 2 (the title comes with)
Input example 3 (self compiled, special case - N1 and N2 are 0)
Input example 4 (self compiled, normal)
Input example 5 (self compiled, normal)
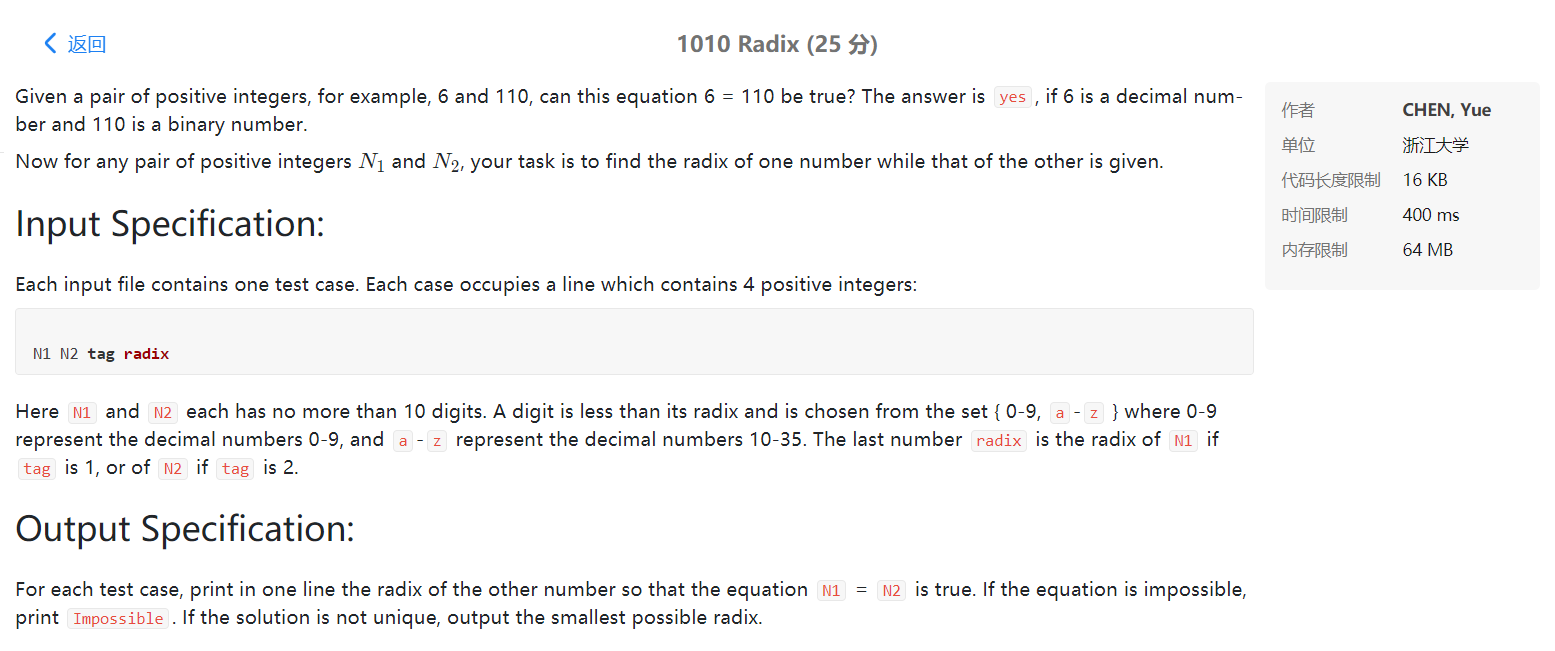
Summary of test points, pits and problems needing attention
Screenshot of submission results of sequential search method
Screenshot of dichotomy submission results
Two kinds of problem solving ideas and source code
1. Common solution - sequential search (24 points, test point 7 fails)
2. Efficient solution - binary search (AC)
subject
Title Link: 1010 Radix (PAT (Advanced Level) Practice)
Test sample
Input sample 1 (the title comes with it)
6 110 1 10
Output sample 1
2
Input example 2 (the title comes with)
1 ab 1 2
Output sample 2
Impossible
Input example 3 (self compiled, special case - N1 and N2 are 0)
0 0 1 4
Output sample 3
2
Input example 4 (self compiled, normal)
15 1111 1 10
Output sample 4
2
Input example 5 (self compiled, normal)
120000 3b 1 10
Output example 5
Impossible
Summary of test points, pits and problems needing attention
1.int type can store up to 10 digits, and if the data in the title is converted to decimal, it is likely to exceed 10 digits, so it should be stored with long long.
2. Determine the lower bound of the search - because the base of the number must be larger than any bit of the number.
3. To determine the upper bound of the search:
(1) If it is a sequential search, the upper limit of 1000 is enough, because it is useless to set too large, and it will timeout.
(2) If it is a binary search, the upper bound should take the maximum of the decimal value of a known number and the lower bound + 1.
The reasons are:
a. assuming that the decimal value of the known number is 999 and the number to be obtained is 1, the decimal value to be obtained is 999. If the number to be obtained is greater than 1, the decimal value to be obtained must be less than 999, so the upper bound should be at least the decimal value of the known number.
b. if the decimal value of a known number is 1 or 0, the upper bound will be less than the lower bound, which should be avoided.
c. +1 is because mid = (right + left)/2 = (right - left)/2 + left may be rounded, so + 1. (in fact, it's not a big problem if you don't add 1).
4. Note that the required binary value may be greater than 35. If you don't notice this, the score will be very low.
5. A pit that is not easy to find: even if you use long long to store decimal values, it may still overflow. Therefore, it is necessary to judge the overflow (when the calculated decimal value is less than 0).
6. Only using the sequential search method, test point 7 cannot pass and will timeout (the wrong answer in the screenshot is because I didn't increase the upper bound. If the upper bound is adjusted too large, it will prompt that it timed out)
Screenshot of submission results of sequential search method
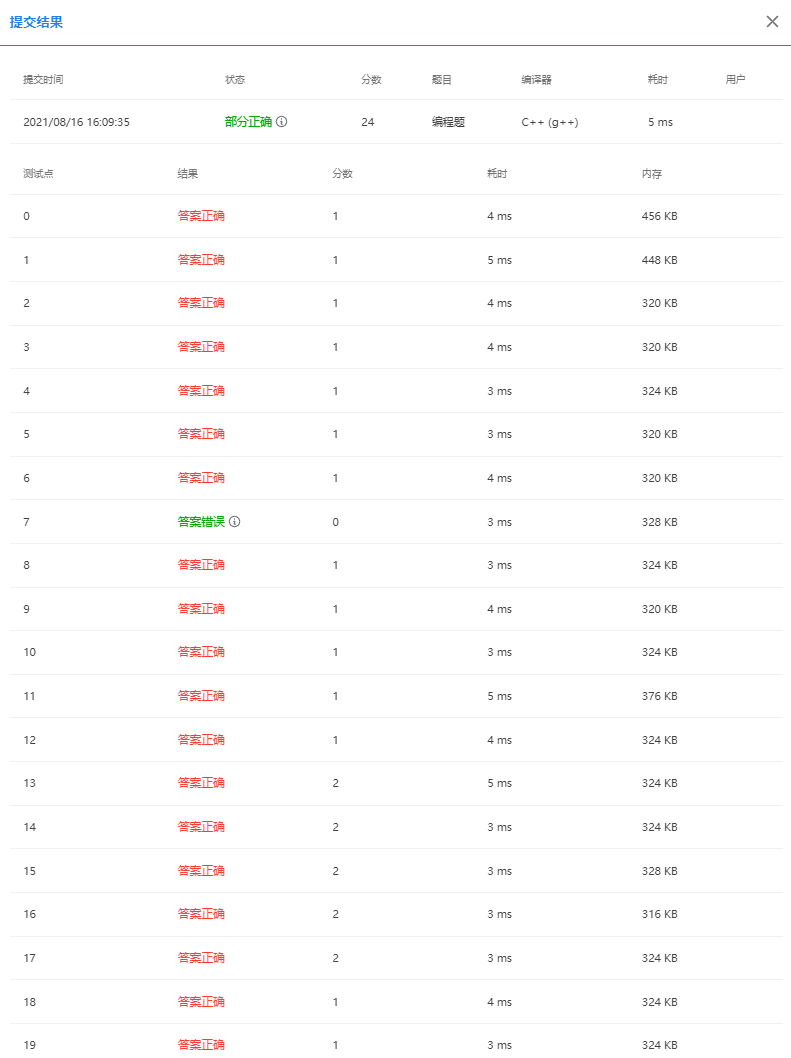
Screenshot of dichotomy submission results
Two kinds of problem solving ideas and source code
1. Common solution - sequential search (24 points, test point 7 fails)
/***************************************************************************
* Problem solving ideas:
* 1.Sample analysis:
* (1)Example 1:
* Input: 6 110 1 10
* Output: 2
* Note 6 is hexadecimal, and when 110 is binary, 6 = 110 is satisfied
* (2)Example 2:
* Input: 1 ab 1 2
* Output: Impossible
* Note 1 is binary, and no matter ab is binary, 1 = ab cannot be satisfied
* 2.According to the example, it can be seen that the decimal value must be larger than the largest digit of the number. For example,
* "45564"At least 7 hexadecimal, "1a3" is at least 11 hexadecimal.
* 3.Calculation method:
* Example: (110) binary = (1 * 2 + 1) * 2 + 0 = (6) decimal
* ->If the two numbers entered are stored in char Num[2][11],
* The values of the two numbers are saved with Num[2] and the length is len[2]
* Suppose the number to be solved is Num[1], the known number is Num[0], and its length is len[0]
* Then find the value of Num[0] first:
* Num[0] = (...(Num[0][0]*radix + Num[0][1])*radix...) + Num[0][len[0]-1]
* Similarly, Num[1] is obtained according to the result of ergodic guess
* Compare Num[0] and Num[1]
* If equal, it ends
* If num [0] < num [1], there is no need to continue traversing the search and end directly.
* If num [0] > num [1], there are equal possibilities.
***************************************************************************/
#include <string.h>
#include <iostream>
using namespace std;
#define con_tag (tag == 1? 2:1)
int tag;//1 or 2
int radix;
char Num[3][11];
int len[3];
long long value[3];
int MaxDigit = -1;
//Convert characters to numbers
int get_true_num(char str)
{
if('0' <= str && str<= '9')
return str - 48;
else if('a' <= str && str <= 'z')
return (str - 'a' + 10);
else
cout<<"Input exception!"<<endl;
return -1;
}
int main()
{
cin>>Num[1]>>Num[2]>>tag>>radix;
for(int i = 1; i < 3; i++)
len[i] = strlen(Num[i]);
value[tag] = get_true_num(Num[tag][0]);
for(int i = 1; i < len[tag]; i++)
value[tag] = value[tag]*radix + get_true_num(Num[tag][i]);
for(int i = 0; i < len[con_tag]; i++)
if(MaxDigit < get_true_num(Num[con_tag][i]))
MaxDigit = get_true_num(Num[con_tag][i]);
for(long long i = MaxDigit + 1; i < 1000; i++)
{
value[con_tag] = get_true_num(Num[con_tag][0]);
for(int j = 1; j < len[con_tag]; j++)
value[con_tag] = value[con_tag]*i + get_true_num(Num[con_tag][j]);
if(value[tag] == value[con_tag])
{
cout<<i;
return 0;
}
else if(value[tag] < value[con_tag])
{
cout<<"Impossible";
return 0;
}
}
cout<<"Impossible";
return 0;
}
/*
120000 3b 1 10
6 110 1 10
*/
2. Efficient solution - binary search (AC)
The idea is actually relatively simple. It's changed to binary search. If you don't understand it, you can leave a message and ask me.
#include <string.h>
#include <algorithm>
#include <iostream>
using namespace std;
#define con_tag (tag == 1? 2:1)
typedef long long int ll;
int tag;//1 or 2
int radix;
char Num[3][11];//Num[0] no
int len[3];//len[0] no
ll value[3];//value[0] no
int MaxDigit = -1;
ll res = 0;
//Convert characters to numbers
int get_true_num(char str)
{
if('0' <= str && str<= '9')
return str - 48;
else if('a' <= str && str <= 'z')
return (str - 'a' + 10);
}
//Calculate decimal value
ll get_value(int cur_tag, int length, ll radix)
{
ll sum = 0;
for(int i = 0; i < length; i++)
{
sum *= radix;
sum += get_true_num(Num[cur_tag][i]);
if(sum < 0)
return -1;
}
return sum;
}
ll solve()
{
if(MaxDigit == 0)
MaxDigit++;
ll left = MaxDigit+1, right = max(left, value[tag])+1, mid;
while(left <= right)
{
mid = (right-left)/2+left;
value[con_tag] = get_value(con_tag, len[con_tag], mid);
if(value[tag] == value[con_tag])
{
res = mid;
break;
}
else if((value[tag] < value[con_tag]) || (value[con_tag] == -1))
//value[con_tag] = -1 is beyond the range represented by long long
right = mid - 1;
else
left = mid + 1;
}
return res;
}
int main()
{
cin>>Num[1]>>Num[2]>>tag>>radix;
for(int i = 1; i < 3; i++)
len[i] = strlen(Num[i]);
value[tag] = get_value(tag, len[tag], radix);
for(int i = 0; i < len[con_tag]; i++)
if(MaxDigit < get_true_num(Num[con_tag][i]))
MaxDigit = get_true_num(Num[con_tag][i]);
if(!solve())
cout<<"Impossible";
else
cout<<res;
return 0;
}