Four methods of single linked list inversion or transpose

The reversal of the linked list is essentially to reverse the contents of the linked list:
If the data stored in the linked list is: 1 - > 2 - > 3 - > 4 - > 5;
After the reversal, it is: 5 - > 4 - > 3 - > 2 - > 1;

Here are four methods to reverse the linked list: (the data is represented by 1 - > 2 - > 3, and after reversal, it is 3 - > 2 - > 1)

1. Implemented by stack

The general idea is:
1. First put the contents of the linked list on the stack in turn, and use the stack to record the contents of the linked list
2. Then exit the stack in turn and update the data in the linked list
3. The idea of this method is simple and easy to understand, but the space complexity is O(n), the time complexity is O(n), and the space complexity is large, so it is not recommended to use it.
Code implementation:

void translateLinklist(Linklist& L)
{
	stack<int> stk;//Define stack
	
	Linklist p = L->next;
	while (p)  //Read the contents of the stack in turn, which is the first step
	{
		stk.push(p->data);
		p = p->next;
	}

	p = L->next;
	while (p)   //Out of the stack in turn and replace the data in the linked list, that is, the second step
	{
		p->data = stk.top();
		stk.pop();
		p = p->next;
	}
}

2. Head insertion method

Head insertion means that the nodes are placed in the next position of the head node in turn.
Why can header insertion reverse the linked list?
Imagine that if we put each node of the linked list (except the head node) behind the head node one by one in order, can we reverse the linked list? (as shown in the figure)

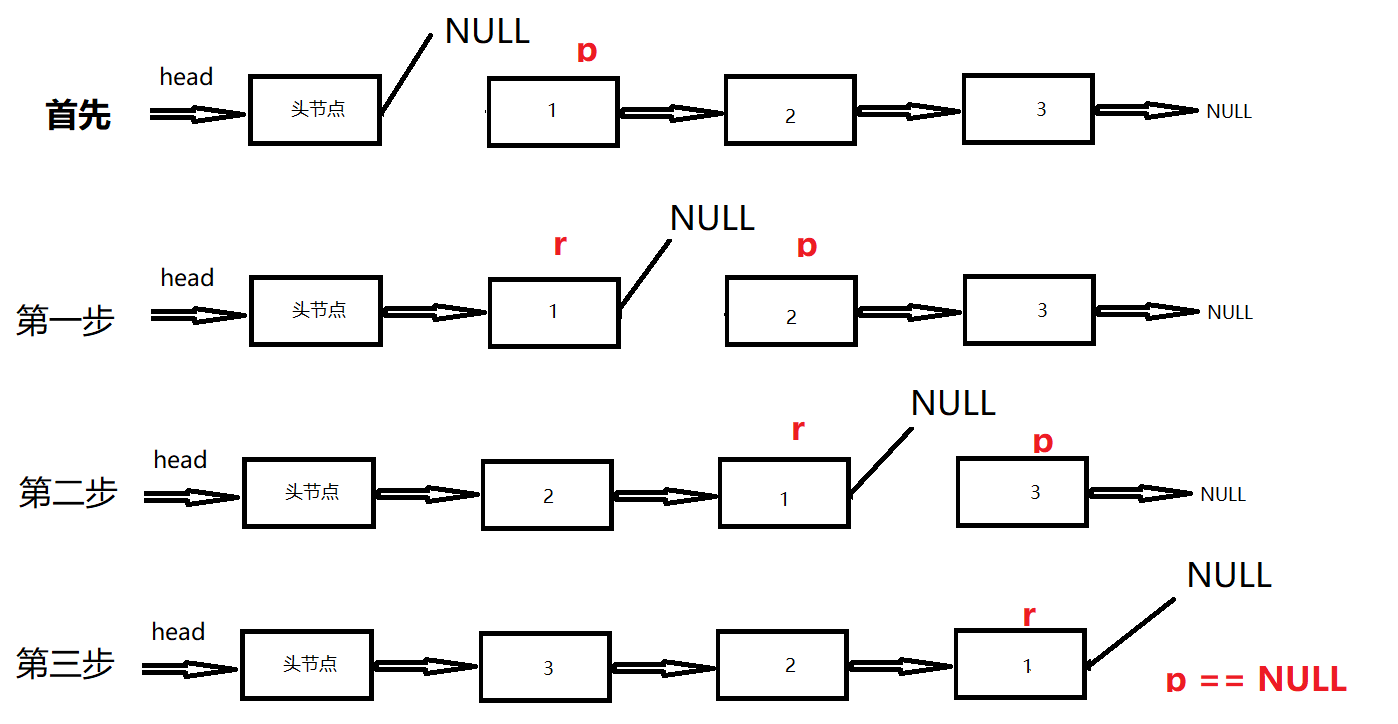
1. The temporary variable r is used to implement the header insertion of the current node;
2. Then, the temporary variable p is used to record R - > next, that is, the next element of the header insertion position, so that the next header insertion element can be found.
3. Space complexity O(1), time complexity O(n)

Code implementation:

void translateLinklist(Linklist& L)  //Inversion of linked list by head interpolation
{
	Linklist p;			//Used to record p the next position 
	Linklist r;			//Record the position of p for head insertion
	p = L->next;		//Use p to record the contents after the header node
	L->next = NULL;		//Empty the head point of the list first
	while (p)
	{
		r = p;			//Use r to record the position of the current p
		p = p->next;    //Use p to constantly find the next element
		r->next = L->next; //Perform head insertion
		L->next = r;
	}
}

3. Three finger acupuncture (also known as local reversal method)

Three pointers:
Linklist cur: records the current node;
Linklist pre: records the previous node of the current node;
Linklist r: record the next node of the current node (i.e. the remaining nodes);
In the process of reversing the linked list, as long as we make the current node cur point to the previous node pre, do we basically realize the reversal of these two nodes?
Yes, that's it, so how to realize all node inversion?
This is simple. After cur points to pre, we move the pre position of the previous node to cur, and then move cur to its next node. How can we record its next node? Didn't we use r to record it before, just move cur to R.
This cycle goes on in turn. Finally, point the pointer of the head node to cur, and the reversal of the linked list is realized. (as shown in the figure)

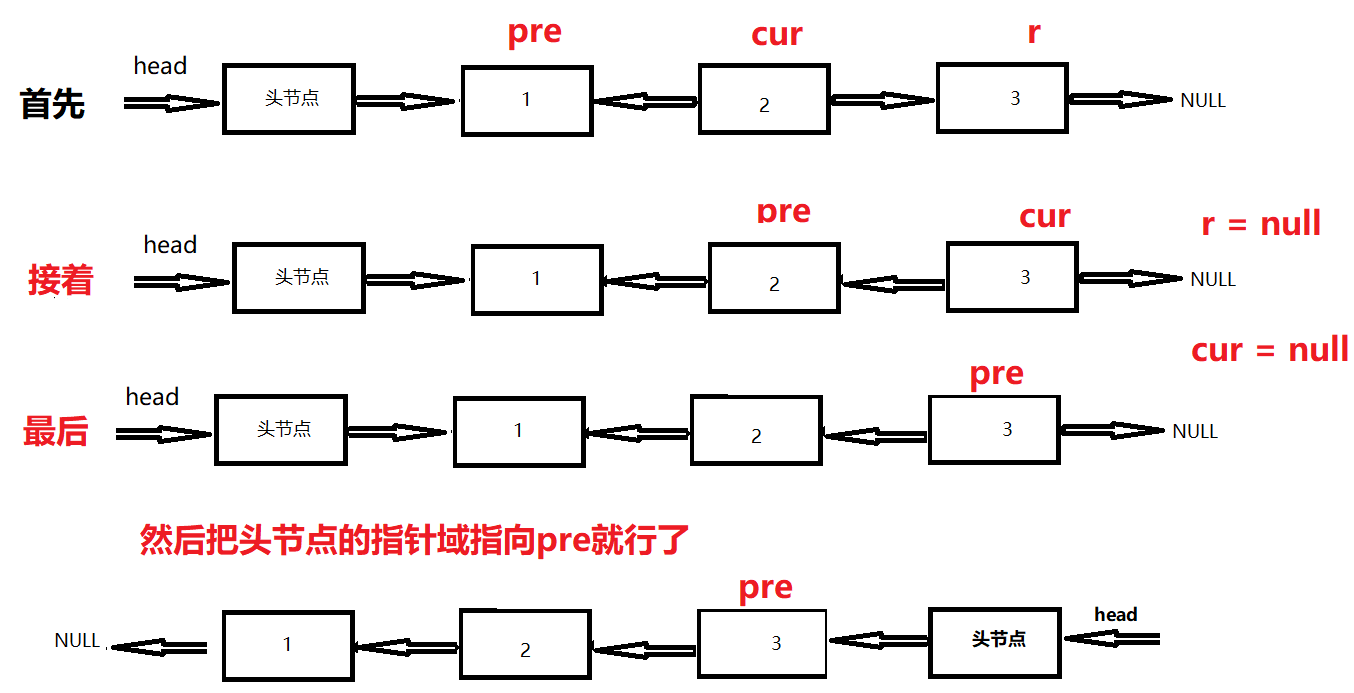
matters needing attention:

1. Finally, make sure that the pointer field of the header node points to pre, because cur is empty at this time.
2. Be sure to make cur point to pre first, that is, turn direction. Then move pre to the position of cur, that is, move backward.
3. The next node of cur must be recorded with r before the last cur points to R, that is, the next node of cur.
4. Space complexity O(1), time complexity O(n).

Code implementation:

void translateLinklist(Linklist& L) //Three finger needle method to reverse the linked list
{
	Linklist pre;	// Record previous nodes
	Linklist cur;	// Record the current node
	Linklist r;		// Record the remaining nodes

	pre = NULL;		 //First set the pre pointer to null
	cur = L->next;   //Point to the first node
	while (cur)
	{
		r = cur->next;  //In this way, r will not become a wild pointer, and this step must be at the front. That is, when cur is not empty, it points to the next one
		cur->next = pre; //Direction of rotation
		pre = cur;      //Move back
		cur = r;
	}
	//After completion, cur is empty, so l - > next should point to pre;
	L->next = pre;
}

4. Recursive method

The purpose of recursion is to find the location of the last node, and then start from the last node and constantly change the location relationship between the last node and its previous node. (as shown in the figure)

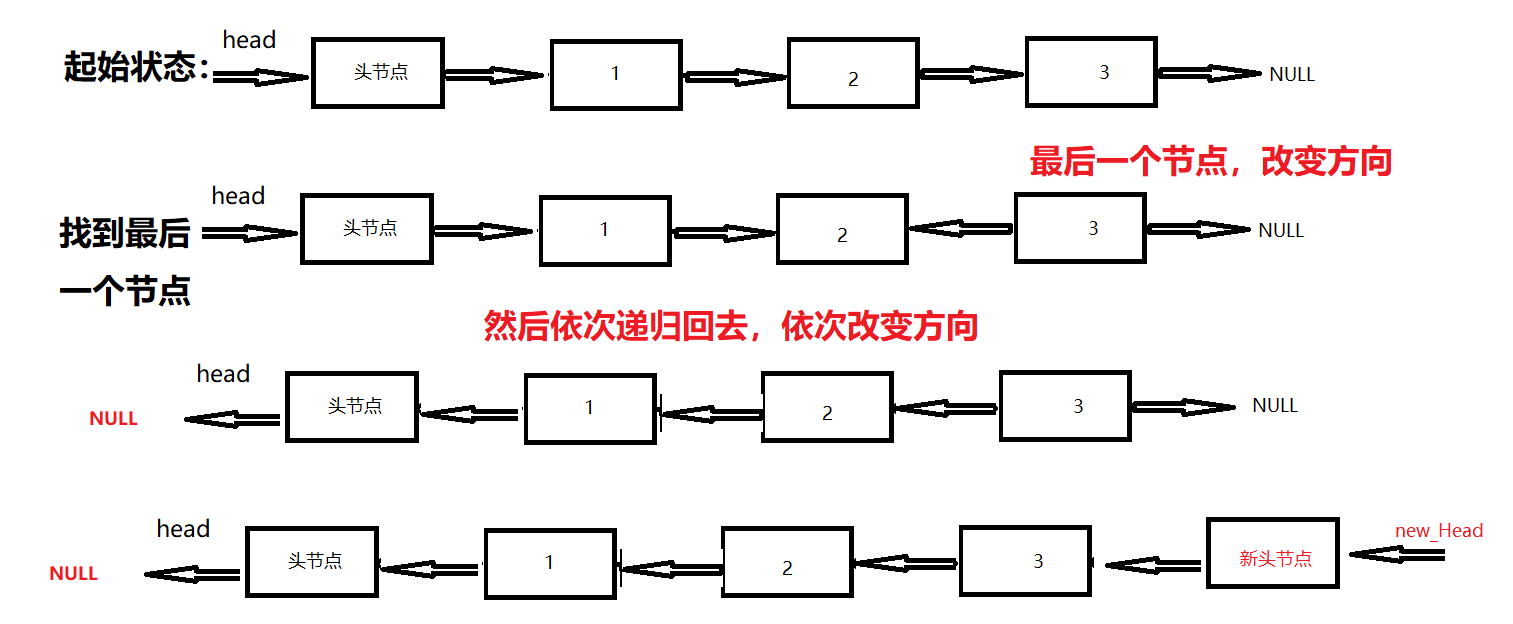
matters needing attention:

1. The head node cannot be deleted during recursion, so the recursion method is suitable for the inversion of linked lists without head nodes, which is also a disadvantage of the recursion method;
2. The location of the last node should be recorded with a new header node, so after finding the node, the node should be returned through a function, that is, newHead in the code;
3. Reverse operation: L - > next - > next = L. here's an explanation: L - > next is the next pointer, and L - > next - > next is the direction of the next pointer, so let the direction of the next pointer point to the current pointer, so as to realize reverse.
4. Finally, make L - > next = null, that is, cut off the original positive direction.
5. The space complexity is O(n), and the time complexity is O(n)

The code is as follows:

Linklist translateLinklist(Linklist& L)
{
	if (L == NULL || L->next == NULL)
	{
		return L;
	}
	else
	{
		Linklist newHead = digui(L->next);
		L->next->next = L;
		L->next = NULL;
		return newHead;
	}
}

Finally, I suggest to master the head insertion method, three finger needle method and recursive method, and understand the method realized by stack. The recursive method is best used for single linked lists without header nodes. The head interpolation method and three pointer method can be used in any single linked list.

I am not good at learning. If there are mistakes and omissions, please point them out!