Reason: js handles the addition, subtraction, multiplication and division of decimals according to binary system, and expands or inversely expands the precision of arg2 on the basis of arg1. Therefore, the following situations will occur
The decimal point addition, subtraction, multiplication and division of javascript(js) is a js bug, such as 0.3 * 1 = 0.299999999. The following lists four js algorithms that can perfectly calculate the corresponding accuracy
function accDiv(arg1,arg2){
var t1=0,t2=0,r1,r2;
try{t1=arg1.toString().split(".")[1].length}catch(e){}
try{t2=arg2.toString().split(".")[1].length}catch(e){}
with(Math){
r1=Number(arg1.toString().replace(".",""))
r2=Number(arg2.toString().replace(".",""))
return accMul((r1/r2),pow(10,t2-t1));
}
}
//multiplication
function accMul(arg1,arg2)
{
var m=0,s1=arg1.toString(),s2=arg2.toString();
try{m+=s1.split(".")[1].length}catch(e){}
try{m+=s2.split(".")[1].length}catch(e){}
return Number(s1.replace(".",""))*Number(s2.replace(".",""))/Math.pow(10,m)
}
//addition
function accAdd(arg1,arg2){
var r1,r2,m;
try{r1=arg1.toString().split(".")[1].length}catch(e){r1=0}
try{r2=arg2.toString().split(".")[1].length}catch(e){r2=0}
m=Math.pow(10,Math.max(r1,r2))
return (arg1*m+arg2*m)/m
}
//subtraction
function Subtr(arg1,arg2){
var r1,r2,m,n;
try{r1=arg1.toString().split(".")[1].length}catch(e){r1=0}
try{r2=arg2.toString().split(".")[1].length}catch(e){r2=0}
m=Math.pow(10,Math.max(r1,r2));
n=(r1>=r2)?r1:r2;
return ((arg1*m-arg2*m)/m).toFixed(n);
} Let's specifically analyze the loss of digital accuracy in JavaScript
1, Some typical problems of JS digital accuracy loss
1. Add two simple floating-point numbers
| 1 | 0.1 + 0.2 != 0.3 // true |
Firebug

This is really not a Firebug problem. You can try alert (ha ha, kidding).
Look at the calculation results of Java
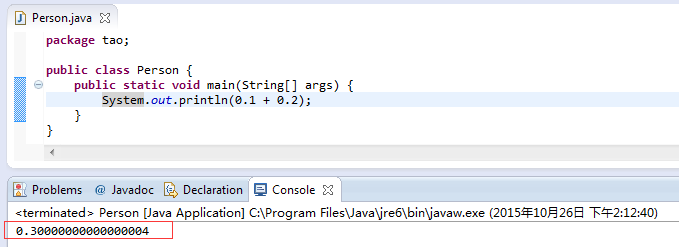
Look at Python

2. Large integer operation
| 1 | 9999999999999999 == 10000000000000001 // ? |
Firebug
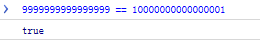
It's unreasonable that 16 digits and 17 digits are equal.
Another example
| 1 2 | var x = 9007199254740992 x + 1 == x // ? |
Look at the results

The Three Outlooks have been subverted again.
3. toFixed Not rounded(Chrome)
| 1 | 1.335.toFixed(2) // 1.33 |
Firebug
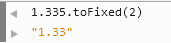
On the Internet, the price in Chrome is inconsistent with that in other browsers, which is caused by the toFixed compatibility problem
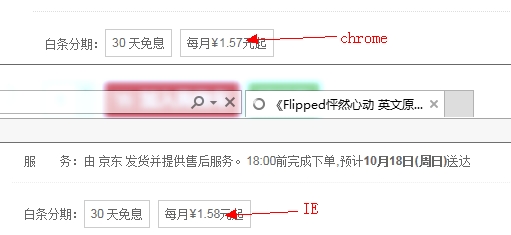
2, Reasons for JS digital loss of accuracy
The binary implementation and bit limit of the computer, some numbers can not be limited. Just like some irrational numbers cannot be expressed finitely, such as PI 3.1415926, 1.3333... Wait. JS compliance IEEE 754 Specification, double precision storage is adopted, occupying 64 bit s, as shown in the figure
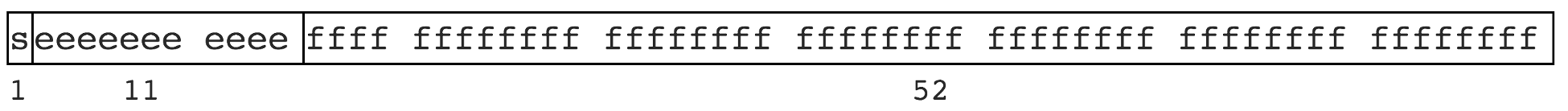
significance
- 1 bit is used to represent the symbol bit
- 11 bits are used to represent the index
- 52 bits indicate mantissa
Floating point numbers, such as
| 1 2 | 0.1 > > 0.0001 1001 1001... (1001 infinite loop) 0.2 > > 0.0011 0011 0011... (0011 infinite loop) |
At this time, you can only imitate the decimal system for rounding, but the binary system has only 0 and 1, so it becomes 0 to 1. This is the fundamental reason for the error and loss of accuracy in some floating-point operations in the computer.
The precision loss of large integers is essentially the same as that of floating-point numbers. The maximum trailing digit is 52 bits, so the maximum integer that can be accurately represented in JS is math Pow (2, 53), decimal system, i.e. 9007199254740992.
Greater than 9007199254740992 may lose accuracy
| 1 2 3 | 9007199254740992 >> 10000000000000... 0 / / 53 in total 9007199254740992 + 1 >> 10000000000000... 001 / / 52 zeros in the middle 9007199254740992 + 2 >> 10000000000000... 010 / / 51 zeros in the middle |
actually
| 1 2 3 4 | 9007199254740992 + 1 / / missing 9007199254740992 + 2 / / not lost 9007199254740992 + 3 / / missing 9007199254740992 + 4 / / not lost |
The results are shown in the figure
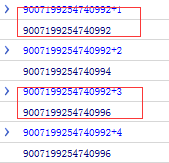
From the above, we can know that seemingly poor numbers are infinite in the binary representation of the computer. Due to the limitation of storage bits, there is "rounding", and the loss of accuracy occurs.
For more in-depth analysis, see this paper (long and smelly): What Every Computer Scientist Should Know About Floating-Point Arithmetic
3, Solution
For integers, the probability of front-end problems may be relatively low. After all, very few businesses need to use very large integers, as long as the operation result does not exceed math Pow (2, 53) will not lose accuracy.
For decimals, there are still many chances of problems at the front end, especially when some e-commerce websites involve data such as amount. Solution: put the decimal to the integer (multiply by multiple), and then reduce it back to the original multiple (divide by multiple)
| 1 2 | // 0.1 + 0.2 (0.1*10 + 0.2*10) / 10 == 0.3 // true |
The following is an object I wrote to mask the loss of precision in the addition, subtraction, multiplication and division of decimals. Of course, the converted integer still cannot exceed 9007199254740992.
/**
* floatObj It includes four methods of addition, subtraction, multiplication and division, which can ensure that the precision of floating-point operation is not lost
*
* We know that floating-point number calculation in computer programming language will have the problem of precision loss (or rounding error). The fundamental reason is the limitation of binary and implementation bits, and some numbers can not be limited
* The following is the binary representation of decimal decimals
* 0.1 >> 0.0001 1001 1001 1001...(1001 Infinite loop)
* 0.2 >> 0.0011 0011 0011 0011...(0011 Infinite loop)
* The storage of each data type in the computer is a limited width. For example, JavaScript uses 64 bit to store digital types, so the excess will be discarded. The missing part is the part where the accuracy is lost.
*
* ** method **
* add / subtract / multiply /divide
*
* ** explame **
* 0.1 + 0.2 == 0.30000000000000004 ((0.00000000000000000004)
* 0.2 + 0.4 == 0.6000000000000001 ((0.0000000000000000001)
* 19.9 * 100 == 1989.9999999999998 ((0.0000000000000000002 less)
*
* floatObj.add(0.1, 0.2) >> 0.3
* floatObj.multiply(19.9, 100) >> 1990
*
*/
var floatObj = function() {
/*
* Judge whether obj is an integer
*/
function isInteger(obj) {
return Math.floor(obj) === obj
}
/*
* Converts a floating-point number to an integer and returns an integer and multiple. If 3.14 > > 314, the multiple is 100
* @param floatNum {number} decimal
* @return {object}
* {times:100, num: 314}
*/
function toInteger(floatNum) {
var ret = {times: 1, num: 0}
if (isInteger(floatNum)) {
ret.num = floatNum
return ret
}
var strfi = floatNum + ''
var dotPos = strfi.indexOf('.')
var len = strfi.substr(dotPos+1).length
var times = Math.pow(10, len)
var intNum = parseInt(floatNum * times + 0.5, 10)
ret.times = times
ret.num = intNum
return ret
}
/*
* The core method realizes addition, subtraction, multiplication and division to ensure no loss of accuracy
* Idea: enlarge the decimal to integer (multiply), perform arithmetic operation, and then reduce it to decimal (divide)
*
* @param a {number} Operand 1
* @param b {number} Operand 2
* @param digits {number} Precision, the number of decimal points reserved, such as 2, is reserved as two decimal places
* @param op {string} Operation type, including add/subtract/multiply/divide
*
*/
function operation(a, b, digits, op) {
var o1 = toInteger(a)
var o2 = toInteger(b)
var n1 = o1.num
var n2 = o2.num
var t1 = o1.times
var t2 = o2.times
var max = t1 > t2 ? t1 : t2
var result = null
switch (op) {
case 'add':
if (t1 === t2) { // The two decimal places are the same
result = n1 + n2
} else if (t1 > t2) { // o1 decimal places greater than o2
result = n1 + n2 * (t1 / t2)
} else { // o1 decimal places less than o2
result = n1 * (t2 / t1) + n2
}
return result / max
case 'subtract':
if (t1 === t2) {
result = n1 - n2
} else if (t1 > t2) {
result = n1 - n2 * (t1 / t2)
} else {
result = n1 * (t2 / t1) - n2
}
return result / max
case 'multiply':
result = (n1 * n2) / (t1 * t2)
return result
case 'divide':
result = (n1 / n2) * (t2 / t1)
return result
}
}
// Four interfaces for addition, subtraction, multiplication and division
function add(a, b, digits) {
return operation(a, b, digits, 'add')
}
function subtract(a, b, digits) {
return operation(a, b, digits, 'subtract')
}
function multiply(a, b, digits) {
return operation(a, b, digits, 'multiply')
}
function divide(a, b, digits) {
return operation(a, b, digits, 'divide')
}
// exports
return {
add: add,
subtract: subtract,
multiply: multiply,
divide: divide
}
}();
The fix for toFixed is as follows
// toFixed repair
function toFixed(num, s) { //The precision of this method still seems to be lost
var times = Math.pow(10, s)
var des = num * times + 0.5
des = parseInt(des, 10) / times
return des + ''
}
function toFixed(len) {
len = len < 0 ? 0 : len;
var num = Math.pow(10, len); //Expansion multiple
return Math.round(accMul(this, num)) / num;
}Reproduced at: https://www.jb51.net/article/85463.htm