Algorithm design and Analysis Experiment 8: backtracking method
1. Subjective questions (10 points)
Experiment 8: use the backtracking algorithm to solve the Sum It Up problem (complete the contents of experiment report 3, 4, 5 and 6)
1, Experimental purpose
Practice using backtracking algorithms to solve practical problems (implemented in the Java language).
2, Experimental content
[problem description]
Give an n,k, and then give n numbers, output all combinations that may make the sum of several numbers equal to k, and exit when the input values of N and k are 0.
3, Program code
(1)SumItUp
package sumItUp;
import java.util.Scanner;
public class SumItUp {
public int sum0;
public int maxSum;
public int nowSum;
private int[] num;//=new int[7];// Change it first to facilitate debugging
public int numberOfNum;
public int numSum;
private boolean[] picking;//=new boolean[7];
public void input(){
Scanner scanner=new Scanner(System.in);
System.out.println("Please enter the value you want to add:");
numSum=scanner.nextInt();
System.out.println("Please enter the total number of numbers:");
numberOfNum=scanner.nextInt();
num=new int[numberOfNum];
picking=new boolean[numberOfNum];
System.out.println("Please enter the corresponding number:");
for (int i=0;i<numberOfNum;i++){
num[i]=scanner.nextInt();
}
}
public void outputData(boolean[] picking){
int lastTrueLocation=0;
for (int i=0;i<numberOfNum;i++){
if (picking[i]==true) {
lastTrueLocation=i;
}
}
for (int j=0;j<numberOfNum;j++){
if (picking[j]==true){
if(j!=lastTrueLocation)
{
System.out.print(num[j]+"+");
}else {
System.out.print(num[j]);
}
}
}
System.out.println("\n");
}
double bound(int i) //Calculate the upper bound (i.e. the total value of the remaining items)
{
//The remaining items are the {i~n} items
int rp=0;
while(i<numberOfNum) //Load items in descending order of value per unit weight
{
rp+=num[i];
i++;
}
return nowSum+rp;
}
public void backtrack(int t){
if(t>numberOfNum-1)//The leaf node has been reached
{
return;
}
if (nowSum+num[t]==numSum){
picking[t]=true;
nowSum+=num[t];
outputData(picking);
nowSum-=num[t];
picking[t]=false;
backtrack(t+1);
}
if(nowSum+num[t]<numSum) //If the constraints are met, the left subtree is searched
{
picking[t]=true;
nowSum+=num[t];
backtrack(t+1);
nowSum-=num[t];
}
if(bound(t+1)>numSum) //If the constraints are met, the right subtree is searched
{
picking[t]=false;
backtrack(t+1);
}
}
}(2)Test
package sumItUp;
import java.util.Scanner;
public class Test {
public static void main(String[] arg){
//4 7 6 4 3 2 2 1 1
//5 4 3 2 1 1
//400 13 12 50 50 50 50 50 50 25 25 25 25 25 25
int test=1;
Scanner scanner=new Scanner(System.in);
while (test==1){
System.out.println("Start the test!");
SumItUp sumItUp=new SumItUp();
sumItUp.input();
sumItUp.backtrack(0);
System.out.println("Please enter whether to continue the test (to continue the test, enter 1 to stop the test, enter 0)");
test=scanner.nextInt();
}
System.out.println("Stop the test!");
}
}
4, Experimental results (including screenshots of program operation)
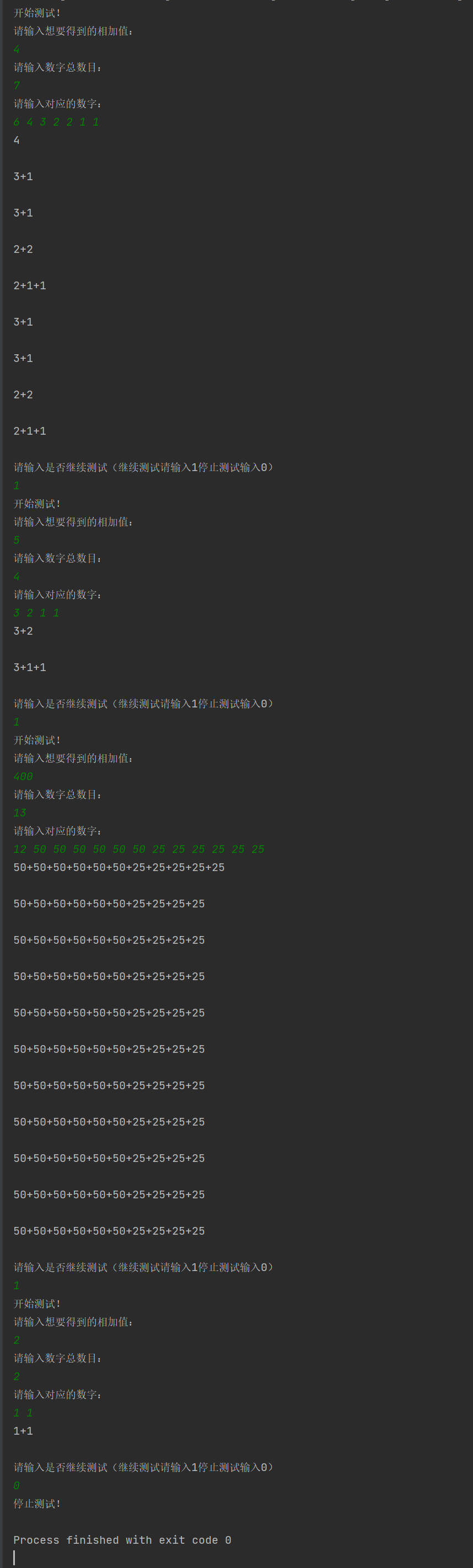
5, Problems and Solutions
There are many problems, and one problem has not been solved yet, that is, how to output a result only once. I want to keep each result and then cycle to compare the same result, and only output one same result. However, I think it is more complex, and the time complexity of my method is relatively high, which is not very cost-effective, So I also want to know if there is a better way.
There are many problems encountered in writing programs, which can be solved one by one through traversal over and over again.
(1) Compared with the teacher's backtracking method, the difference is to output all feasible solutions rather than the optimal solution
Therefore, we can't find the root node to output the solution like the example code, but output one when we find a feasible solution. After finding the feasible solution output, we should go back and traverse the right subtree.
if (nowSum+num[t]==numSum){
picking[t]=true;
nowSum+=num[t];
outputData(picking);// Output the feasible solution at this time
nowSum-=num[t];// Fallback to previous node
picking[t]=false;// Go to right subtree
backtrack(t+1);// Traverse the right subtree
}
At the beginning, the code simply outputs the feasible solution and directly traverses the right subtree without node fallback. Therefore, this problem is found after debug ging. The corrected code is as follows.
(2) The condition for the cyclic right subtree is defined at the beginning when the current sum plus the next number is greater than the required sum,
if(nowSum+num[t]>numSum)
{
picking[t]=false;
backtrack(t+1);
}
It is found that there is no way to use the fallback node after traversing the left subtree: backtrack(t+1);nowSum-=num[t]; After the node goes back, it can only judge whether the value of the current sum plus the next number is greater than the required sum. It is found that if it is not greater than, the right subtree cannot be traversed. Only then can we understand the function of the bound method of the code in the example. The modified right subtree traversal condition is that the sum of the remaining numbers and values is greater than the required sum value.
If (bound (T + 1) > numsum) / / if the restrictions are met, search the right subtree
{
picking[t]=false;
backtrack(t+1);
}
In this way, we can traverse the right subtree after traversing the left subtree. The premise is that the maximum sum of the right subtree is greater than the required sum value, and it is possible to find a feasible solution.
(3) When outputting the feasible solution, you can only traverse the Boolean array of picking. When the value is true, the corresponding output num array and the number at this position. Moreover, since you want to output the plus sign, you need to judge the position of the last true in advance, and the number corresponding to the last number does not output the plus sign.
for (int i=0;i<numberOfNum;i++){
if (picking[i]==true) {
lastTrueLocation=i;// Record the location of the last true
}
}
for (int j=0;j<numberOfNum;j++){
if (picking[j]==true){
if(j!=lastTrueLocation)
{
System.out.print(num[j]+"+");// If true is not the last position, the number and plus sign will be output
}else {
System.out.print(num[j]);// The last position outputs only numbers
}
}
}
(3) Since we output when we find the feasible solution, in the example, when the input number is exactly the required sum value, we don't need to take it as a special case at first. Later, we found this redundant code in the process of debug ging. It is as follows:
for (int i=0;i< sumItUp.numberOfNum;i++){
sumItUp.maxSum+=sumItUp.num[i];
}
if (sumItUp.maxSum==sumItUp.numSum){
System.out.println("sum value is the sum of input numbers!");
}else {
sumItUp.backtrack(0);
}
In fact, it is not necessary.
6, Experimental experience
The backtracking method in this experiment mainly refers to the routine code given by the teacher. If I write the recursive function of backtracking method myself, I think it is difficult. I found that debug is the best way to understand an algorithm or program. I didn't understand it in class, such as the function of the bound function when traversing the right subtree, But I understood it all when I debugged.