1, Basic elements of greedy algorithm

As the name suggests, greedy algorithms always make the best choice at present. In other words, the greedy algorithm does not consider the overall optimization, and its choice is only the local optimal solution in a sense.

The problems that can be solved by greedy algorithm generally have the following two properties: greedy selection property and optimal substructure property.

>Greedy choice

Greedy choice means that the global optimal solution of the problem can be realized through a series of local optimal choices.

In the greedy selection algorithm, we only make the best choice in the current state, and then consider the corresponding subproblem after making this choice.

The greedy choice can depend on the choice made in the past, but not on the choice made in the future, nor on the solution of the Lai Zi problem.

Greedy algorithms are often carried out in a top-down manner, making successive greedy choices in an iterative manner. Each time a choice is made, the problem is simplified into a smaller subproblem.

For a specific problem, to prove whether it has greedy selectivity, it must be proved that the greedy choice made in each step eventually leads to the overall optimal solution of the problem.

>Optimal substructure

The key to simplify the greedy selection problem into a similar subproblem with smaller scale is that the problem has the property of optimal substructure. That is, the optimal solution of the original problem includes the optimal solution of its subproblem.

>Greedy algorithms do not always produce global optimal solutions

Although the greedy algorithm can not get the overall optimal solution for all problems, it can produce the overall optimal solution for a wide range of problems, such as the minimum spanning tree and the single source shortest path problem of graph. In some cases, even if the greedy algorithm can not get the overall optimal solution, the final result is the approximate solution of the optimal solution.

>Whether the greedy algorithm can produce the overall optimal solution needs to be proved

The proof of the correctness of greedy algorithm is given in the later activity arrangement problem with an example.

2, Classic examples

1. Organization of activities

>Problem description

set up S = { 1 , 2 , . . . , n } S={\{ 1,2,...,n \}} S={1,2,...,n} is a collection of N activities. Each activity uses the same resource. Only one activity can use this resource at the same time. Each activity i i i have a start time s i s_i si # and termination time f i f_i fi​， s i ≤ f i s_i ≤ f_i si​≤fi​ .

If activity i i i and j j j is compatible, then there is s j ≤ f i s_j ≤ f_i sj ≤ fi or s i ≥ f j s_i ≥ f_j si​≥fj​ . The activity scheduling problem is to select the largest compatible activity subset from the given activity set.

>Train of thought analysis

So how should this question be greedy? It can be thought that in order to select the most compatible activities, the end time of each selection is the earliest, that is f i f_i fi ， the smallest activity enables us to choose more activities. Then, whether this idea can solve the problem needs to be proved.

First, it is proved that there is always an optimal activity arrangement scheme starting with greedy selection:

S = { 1 , 2 , . . . , n } S={\{ 1,2,...,n \}} S={1,2,...,n} is n activity sets, [ s i , f i ] [s_i,f_i] [si, fi] is the start time of the activity, and f 1 ≤ f 2 ≤ . . . ≤ f n f_1≤f_2≤...≤f_n f1​≤f2​≤... ≤ fn, to prove greedy selection, that is, to explain that an optimal solution of S's activity selection problem includes activity 1.

set up A ⊆ S A ⊆ S A ⊆ S is an optimal solution of the problem, and A A A, too f i f_i fi) sort. Set its first activity as k k k. The second activity is j j j .

① k = 1, then A is the optimal solution starting with greedy selection
② k != 1. Set B = A − { k } ∪ { 1 } B=A-\{k\}∪\{1\} B=A−{k}∪{1}. Since the activities in a are compatible, f 1 ≤ f k ≤ s j f_1≤f_k≤s_j f1 ≤ fk ≤ sj, so the activities in B are also compatible. In addition, the number of elements in A and B sets is equal, so B is the most active arrangement starting with greedy selection activity 1.

From ① to ②, it can be proved that there is always an optimal activity arrangement scheme starting with greedy selection.

Then prove that it has the optimal substructure:

Further, after selecting activity 1, the original problem is simplified to A sub problem of arranging all activities compatible with activity 1 in S. That is, if A is the optimal solution of the original problem, then A '= A - {1} is the activity scheduling problem S ′ = { i ∈ S ∣ s i ≥ f 1 } S' = \{i∈S | s_i≥f_1\} S ′ = {i ∈ s ∣ si ≥ f1}.

It can be proved that if A 'is not the optimal solution, there is an optimal solution, and B' is the optimal solution of S'. Then, the number of elements of B 'is greater than A', and after adding activity 1 to B ', the number of elements is greater than A, which is contrary to the fact that A is the optimal solution.

This proves that the problem has an optimal substructure.

Finally, it is proved that each step of greedy selection finally leads to the overall optimal solution:

The number of greedy choices is mathematically induced to prove greedy selectivity, that is, it is proved that taking the local optimal every time can finally get the overall optimal result.

① When ∣ A ∣ = 1 |A| = 1 When ∣ A ∣ = 1, it can be obtained from the first proof, and it is obviously tenable without more words

② Set ∣ A ∣ < k |A| < k When ∣ A ∣ < K, the proposition is true

③ When ∣ A ∣ = k |A| = k When ∣ A ∣ = k, by the optimal substructure A = { 1 } ∪ A 1 A=\{1\}∪A_1 A={1}∪A1​， A 1 A_1 A1} yes S 1 = { j ∈ S ∣ s j ≥ f 1 } S_1=\{j∈S|s_j≥f_1\} S1 = {j ∈ s ∣ sj ≥ f1}. By inductive assumptions, ∣ A 1 ∣ < k |A_1| < k ∣ A1 ∣ < K, so A 1 A_1 A1 ￠ is obtained by selecting the local optimal solution each time. also S 1 = { j ∈ S ∣ s j ≥ f 1 } S_1=\{j∈S|s_j≥f_1\} S1 = {j ∈ s ∣ sj ≥ f1} is compatible with activity 1, so A A A also satisfies this proposition.

In fact, the last step of the mathematical induction routine is fixed. Only the first two steps need to be proved to illustrate the correctness of the greedy algorithm

>Code implementation

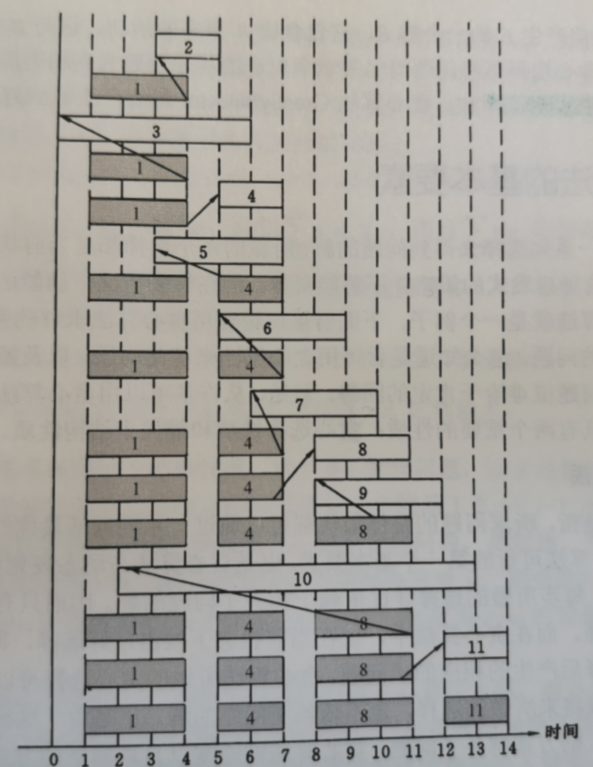
Taking the task arrangement of the following 11 activities as an example, the code implementation is given

#include <iostream>
#include <cstdio>
using namespace std;

const int N = 11;

void GreedSelector(int n, int s[], int f[], bool A[])
{
    A[0] = true;
    int j = 0;
    for (int i = 1; i < N; i++)
    {
        if (s[i] >= f[j])
        {
            A[i] = true;
            j = i;
        }
        else
            A[i] = false;
    }
}

int main()
{
	// By default, f[i] has been arranged in non decreasing order. If there is no arrangement, it needs to be sorted in O(nlogn) time
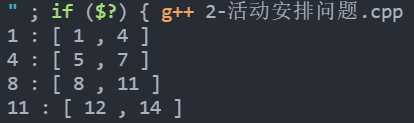
    int s[] = {1, 3, 0, 5, 3, 5, 6, 8, 8, 2, 12};
    int f[] = {4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14};	

    bool A[N];	// Used to judge whether to take or not

    GreedSelector(N, s, f, A);
	
	// Ergodic maximum compatible set
    for (int i = 0; i < N; i++)
        if (A[i])
            cout << i + 1 << " : [ " << s[i] << " , " << f[i] << " ]" << endl;

    return 0;
}

The calculation process and printing results of the algorithm greenselector are as follows:

2. Santa's gift (backpack problem)

>Problem description

Christmas is coming. Santa Claus is ready to distribute candy. Now there are many boxes of different candy. Each box of candy has its own value and weight. Each box of candy can be divided into any bulk combination to take away. Santa Claus's reindeer sleigh can only hold candy weighing W at most. What value candy can Santa Claus take away at most.

In fact, this problem is a variant of the 0-1 knapsack problem. The difference is that it can be divided into any bulk combination.

>Input and output

The first input line consists of two parts: the positive integer n of the number of candy boxes (1 < = n < = 100) and the positive integer w of the maximum weight that reindeer can bear (0 < w < 10000). The two numbers are separated by spaces.

The remaining n lines correspond to a box of candy, which is composed of two parts, which are positive integers of the value of a box of candy respectively v i v_i vi) and weight are positive integers w i w_i wi, separated by a space.

Output the maximum total value of candy that Santa can take away, with 1 decimal place reserved. The output is a line, ending with a newline character.

>Train of thought analysis

In fact, this example is very similar to the 0-1 knapsack problem, except that the items in this problem do not require complete selection, but only parts can be selected.

For this problem, we can first according to the unit weight value of candy v i / w i v_i/w_i vi / wi. Then, select the candy with the highest value per unit weight as far as possible until it reaches the maximum weight that reindeer can bear.

The key to this problem lies in the basis of all kinds of candy v i / w i v_i/w_i vi / wi ， sort from high to low, so the complexity is O ( n l o g n ) O(nlogn) O(nlogn) .

>Code implementation

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const double eps = 1e-6;

struct Candy
{
    int v, w;
    bool operator<(const Candy &c) const
    {
        return double(v) / w - double(c.v) / c.w > eps;
    }
} candies[110];

int main()
{
    int n, w;
    cin >> n >> w;
    for (int i = 0; i < n; ++i)
        cin >> candies[i].v >> candies[i].w;
    sort(candies, candies + n);		

    int totalW = 0;
    double totalV = 0;

    for (int i = 0; i < n; ++i)
    {
        if (totalW + candies[i].w <= w)
        {
            totalW += candies[i].w;
            totalV += candies[i].v;
        }
        else
        {
            totalV += double(w - totalW) * candies[i].v / candies[i].w;
            break;
        }
    }
    printf("%.1f", totalV);
}

>Greedy selection strategy is no longer applicable to 0-1 knapsack problem

For example, consider this example.

There are 3 boxes of candy, with the value and weight of (8,6) (5,5) (5,5) respectively, and the total capacity of the sled is 10. If you choose greedily, you will give priority to (8,6) with a total value of 8. After that, you can't choose other boxes of candy because the remaining capacity is not enough to take another box of candy.

But in fact, the best choice is two boxes (5,5) of candy with a total value of 10.

3. Huffman coding problem

Huffman coding can compress data effectively: it can usually save 20% ~ 90% of the space, and the specific compression rate depends on the characteristics of the data. We treat the data to be compressed as a character sequence. According to the frequency of each character, Huffman greedy algorithm constructs the optimal binary representation of the character.

>Problem description

For example, if a file contains 100000 characters (characters and frequencies are as follows), there are two ways to compress its data: fixed length code and variable length code:

After calculation, the total code length of fixed length coding is 300000, while the total code length of variable length coding is 224000 bits. It can be found that variable length code is much better than fixed length code.

In order to minimize the average code length, Huffman proposed a greedy algorithm to construct the optimal prefix code. The resulting Huffman coding scheme is called Huffman algorithm.

Huffman algorithm constructs the binary tree T of the optimal prefix code in a bottom-up manner. The algorithm starts with | C | leaf nodes and performs | C| - 1 merging operation to generate the final required tree t.

>Train of thought analysis

In short, it is to construct Optimal binary tree (Huffman tree) , but the weight here is the frequency of characters, and the path length is the code length of characters.

It is believed that students who have studied data structure should be familiar with how to construct the optimal binary tree, which can be divided into the following steps:

① Take the frequency f(c) of each character C in the character set as the weight

② According to the given weight { w 1 , w 2 , ⋅ ⋅ ⋅ , w n } \{w_1,w_2,···,w_n\} {w1, w2, ⋅ ⋅, wn} construct n binary trees F = { T 1 , T 2 , ⋅ ⋅ ⋅ , T n } F=\{T_1,T_2,···,T_n\} F={T1, T2, ⋅ ⋅, Tn}, each T i T_i Ti ， has only one root node, and the weight is w i w_i wi​ .

③ In F, select the tree with the smallest weight of two root nodes to form a new binary tree, and the weight of its root is the sum of the weight of the left and right subtree roots.

④ Delete these two trees in F and add the new one.

⑤ Repeat steps ③ and ④ until there is only one tree left.

After generating the optimal binary tree, find the parent node of the leaf node in reverse order and code it.

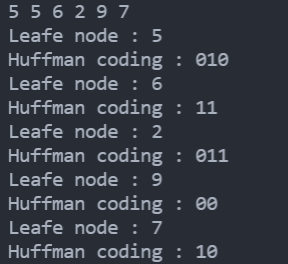
For example, a file is composed of four letters {b, c, j, m, p} with frequencies of {5, 6, 2, 9, 7} to construct a Huffman tree.

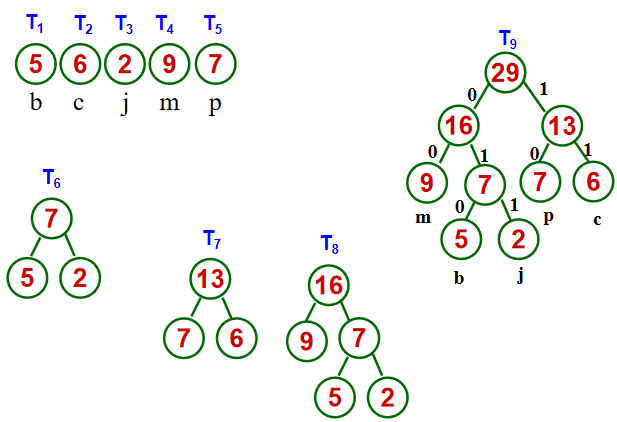
Of course, because the optimal binary tree is not unique, there can be many coding methods for this problem. For the above figure, there are Huffman codes b:010, c:11, j:011, m:00 and p:10

>Code implementation

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;

typedef struct
{
    int weight;
    int parent, lc, rc;
} HTNode, *HuffmanTree;

void SelectMin(HuffmanTree &HT, int n, int &s1, int &s2)
{
    int minum;
    // Find the minimum value first, (const int max = 0x3f3f3f3f can also be defined)
    for (int i = 1; i <= n; i++)
    {
        if (HT[i].parent == 0)
        {
            minum = i;
            break;
        }
    }
    for (int i = 1; i <= n; i++)
    {
        if (HT[i].parent == 0)
            if (HT[i].weight < HT[minum].weight)
                minum = i;
    }
    s1 = minum;

    // Find the second smallest value
    for (int i = 1; i <= n; i++)
    {
        if (HT[i].parent == 0 && i != s1)
        {
            minum = i;
            break;
        }
    }
    for (int i = 1; i <= n; i++)
    {
        if (HT[i].parent == 0 && i != s1)
            if (HT[i].weight < HT[minum].weight)
                minum = i;
    }
    s2 = minum;
}

void CreatHuff(HuffmanTree &HT, int *w, int n)
{
    int m, s1, s2;
    // m is the total number of nodes
    m = n * 2 - 1;

    HT = (HuffmanTree)malloc(m * sizeof(HTNode));

    // Leaf node initialization
    for (int i = 1; i <= n; i++)
    {
        HT[i].weight = w[i];
        HT[i].parent = 0;
        HT[i].lc = 0;
        HT[i].rc = 0;
    }

    // Initialization of non leaf nodes
    for (int i = n + 1; i <= m; i++)
    {
        HT[i].weight = 0;
        HT[i].parent = 0;
        HT[i].lc = 0;
        HT[i].rc = 0;
    }

    // Constantly merge and create Huffman tree
    for (int i = n + 1; i <= m; i++)
    {
        SelectMin(HT, i - 1, s1, s2);

        HT[s1].parent = i;
        HT[s2].parent = i;
        HT[i].rc = s1;
        HT[i].lc = s2;
        HT[i].weight = HT[s1].weight + HT[s2].weight;
		
		// Test print Huffman tree
        // cout << HT[i].weight << " : " << HT[s1].weight << " 1 "
        //      << " , " << HT[s2].weight << " 0 "
        //      << endl;
    }
}

void HuffmanTreeCode(HuffmanTree HT, char *str, int n, int child, int &e)
{
    int j = 0, m = 0;
    int parent = HT[child].parent; //Gets the value of the parent node of the first leaf node

    cout << "Leafe node : " << HT[child].weight << endl;

    //Find root node and generate code: 0 on the left and 1 on the right
    for (int i = n; parent != 0; i--) //parent != -1 the current node is not a root node
        // The current leaf is a left child
        if (HT[parent].lc == child)
        {
            str[j++] = '0';
            child = parent;
            parent = HT[child].parent;
        }
        else // The current leaf is a right child
        {
            str[j++] = '1';
            child = parent;
            parent = HT[child].parent;
        }
    e = j; //Indicates the end of the coding of a leaf node
}

int main()
{
    HuffmanTree HT;

    int *w;   // Storage frequency
    int n, c; // n is the number of nodes and c is the frequency
    cin >> n;

    w = (int *)malloc(n * sizeof(int));
    for (int i = 1; i <= n; i++)
    {
        cin >> c;
        w[i] = c;
    }

    CreatHuff(HT, w, n); // Create Huffman tree

    char str[n]; // Storage coding
    int e = 0; // Record the end of coding

    for (int i = 1; i <= n; i++)
    {
        HuffmanTreeCode(HT, str, n, i, e);
        cout << "Huffman coding : ";
        for (int j = e - 1; j >= 0; j--)
            cout << str[j];
        cout << endl;
    }

    free(w);
    free(HT);

    return 0;
}

For the case shown above, the printing effect is as follows: