Concept and structure
Basic concepts of binary tree
A binary tree is a finite set of nodes, which:
1. Null
2. It is composed of a root node and its left and right subtrees
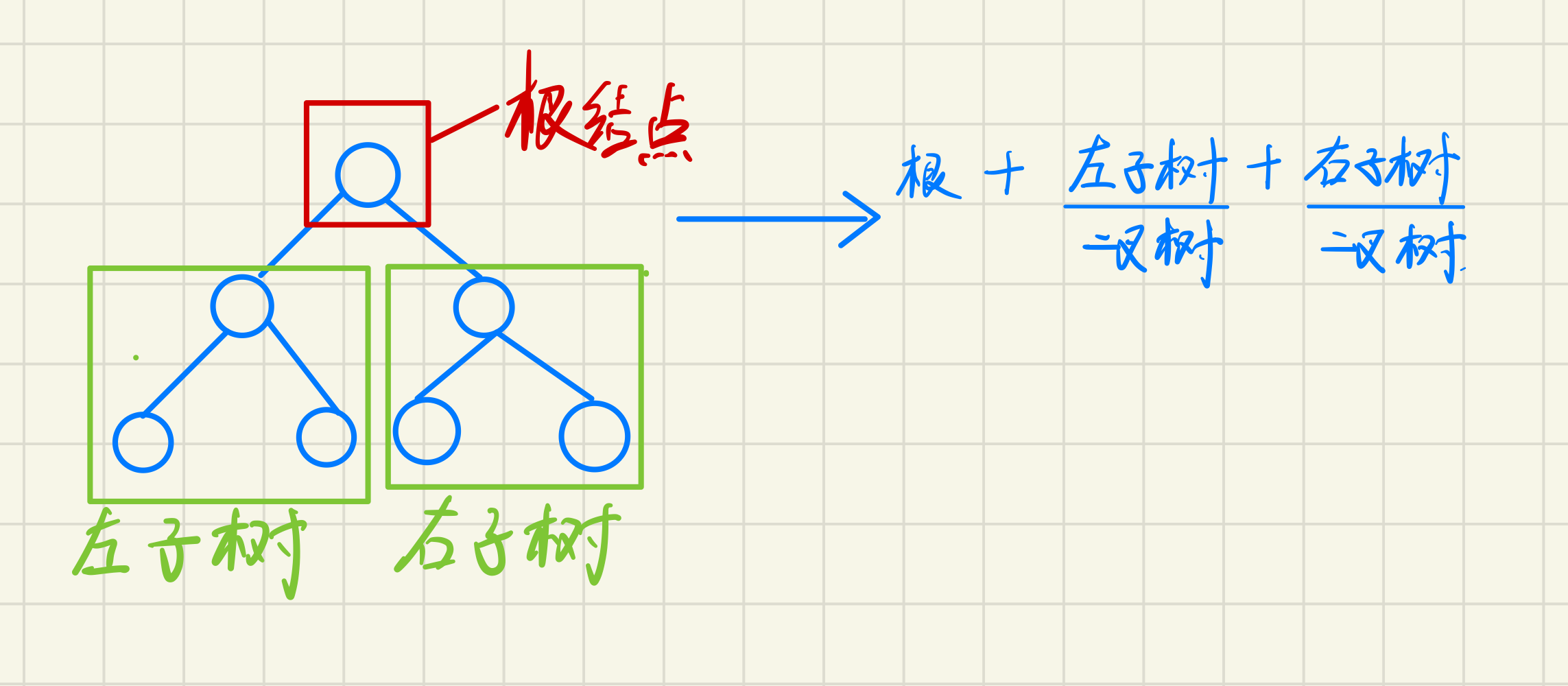
As can be seen from the above figure:
1. The binary tree does not have nodes with a degree greater than 2
2. The subtree of a binary tree can be divided into left and right, and the order cannot be reversed. Therefore, a binary tree is an ordered tree
Special binary tree
Full binary tree
1. It is an empty tree
2. If it is not empty, the number of nodes in each layer of the binary tree reaches the maximum number of nodes that can be accommodated in this layer
That is, when the number of layers is k, the number of summary points is 2^k -1 nodes

Complete binary tree
A complete binary tree is derived from a full binary tree~~
1. It is an empty tree
2. If not empty, for a binary tree with k levels:
The first k-1 layer is a full binary tree
Layer k arranges the number of remaining nodes in order from left to right

Properties of binary tree
1. If the specified number of layers of the root node is 1, there are at most 2^(i-1) nodes on layer I of a non empty binary tree
2. If the specified number of layers of the root node is 1, the maximum number of nodes of the binary tree with depth h is 2^h -1
3. For any binary tree, if the number of nodes with degree 0 is n0 and the number of nodes with degree 2 is n2, the relationship n0 = n2+1 holds
The proof for 3 is as follows:

4. If the specified number of layers of the root node is 1, the depth of the full binary tree with n nodes is h = log(n+1) (indicating the logarithm of log with 2 as the base and n+1)
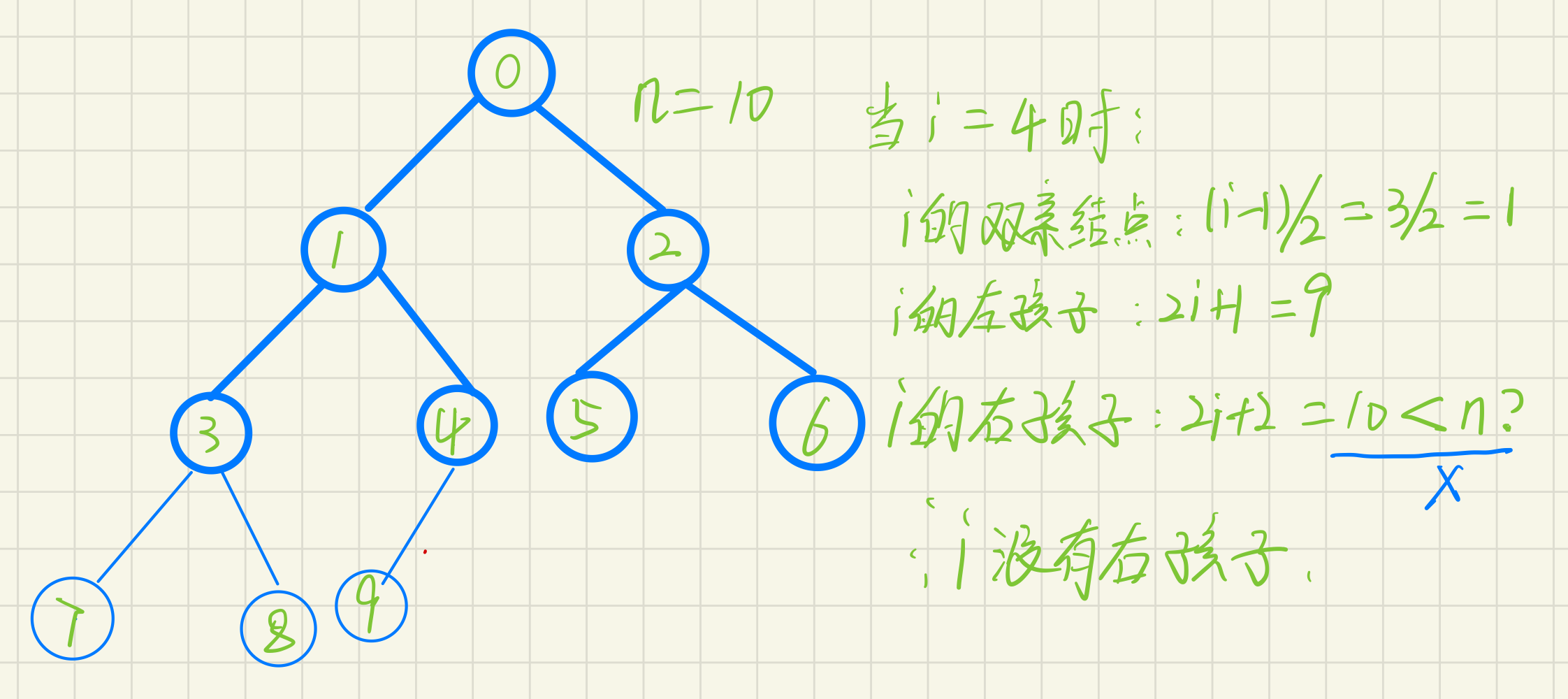
5. For a complete binary tree with n nodes, if all nodes are numbered from 0 in the array order from top to bottom and from left to right, the nodes with sequence number i are:
1. If I > 0, the parent serial number of the node at I position: (i-1) / 2; i = 0, i is the root node number, and there is no parent node
2. If 2i+1 < n, left child serial number: 2i+1, otherwise there is no left child
3. If 2i+2 < n, right child serial number: 2i+2, otherwise there is no right child
Brief description of 5
Storage structure of binary tree
For binary trees, there are generally two storage structures
Sequential storage
Use arrays to store. Generally, arrays are only suitable for representing complete binary trees, because there will be a waste of space if they are not complete binary trees. In reality, only heap will use array to store.
Binary tree sequential storage is physically an array and logically a binary tree
Sequential storage of complete binary tree

Sequential storage of incomplete binary tree

Linked Storage
A binary tree is represented by a linked list
Each node in the linked list consists of three parts, data field and left and right pointer field. The left and right pointer fields respectively point to the nodes where the left and right children of the node are located. At present, binary chain is used to store.
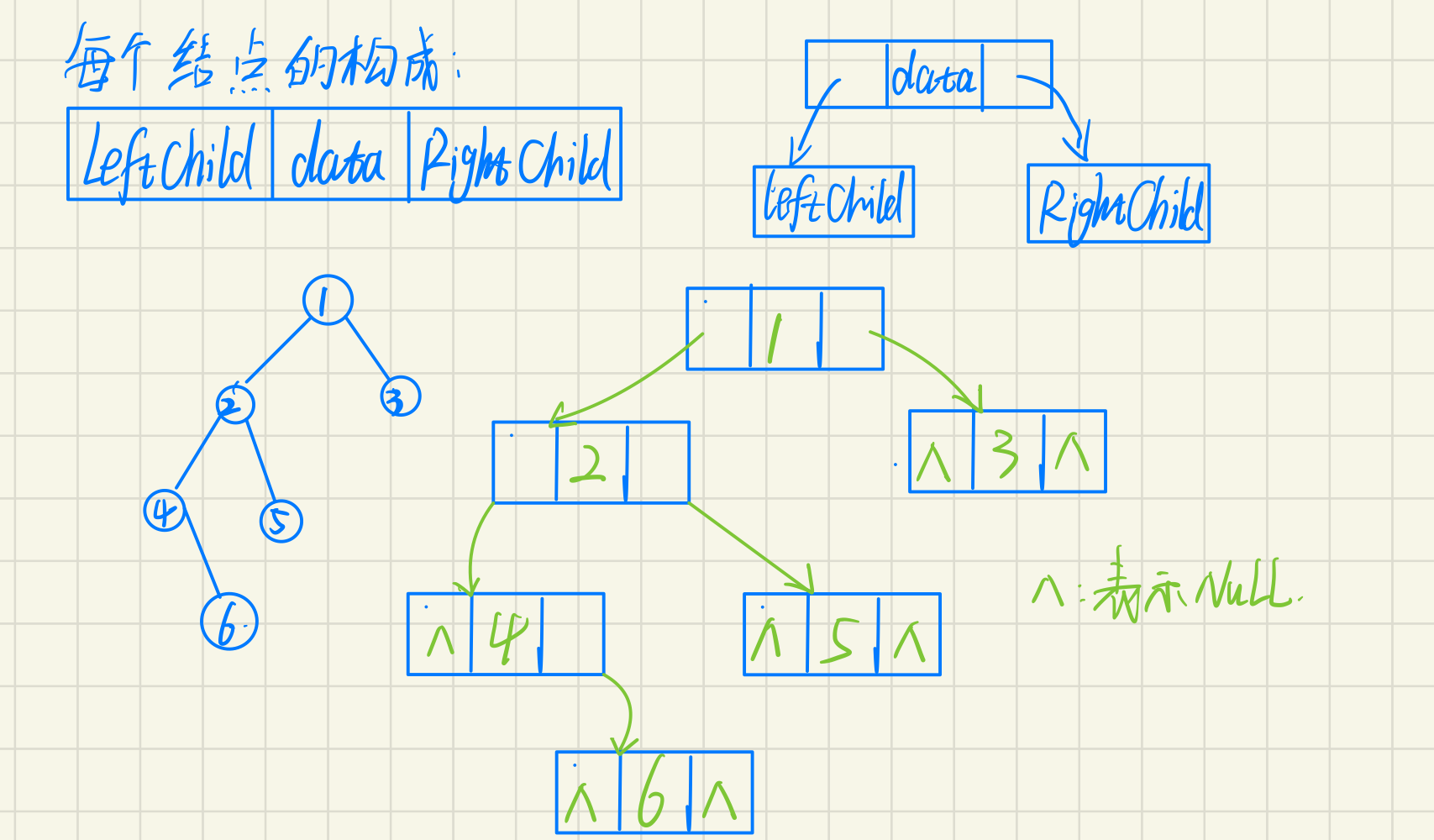
The corresponding data structure type is
typedef char BTDataType;
typedef struct BinaryTree
{
BTDataType data;//Data domain
struct BinaryTree* left;//Points to the left child of the current node
struct BinaryTree* right;//Point to the right child of the current node
}BTNode;
Sequential structure and implementation of binary tree
As mentioned earlier, sequential storage is more practical for complete binary trees. Sequential storage is mainly used to store the heap. The related concepts of heap are introduced below
Concept and structure of reactor
Concept: a set of data is stored in an array in the order of a complete binary tree. This set of data needs to meet the following conditions:
The parent node of the binary tree is always larger than its child node, which is called a heap
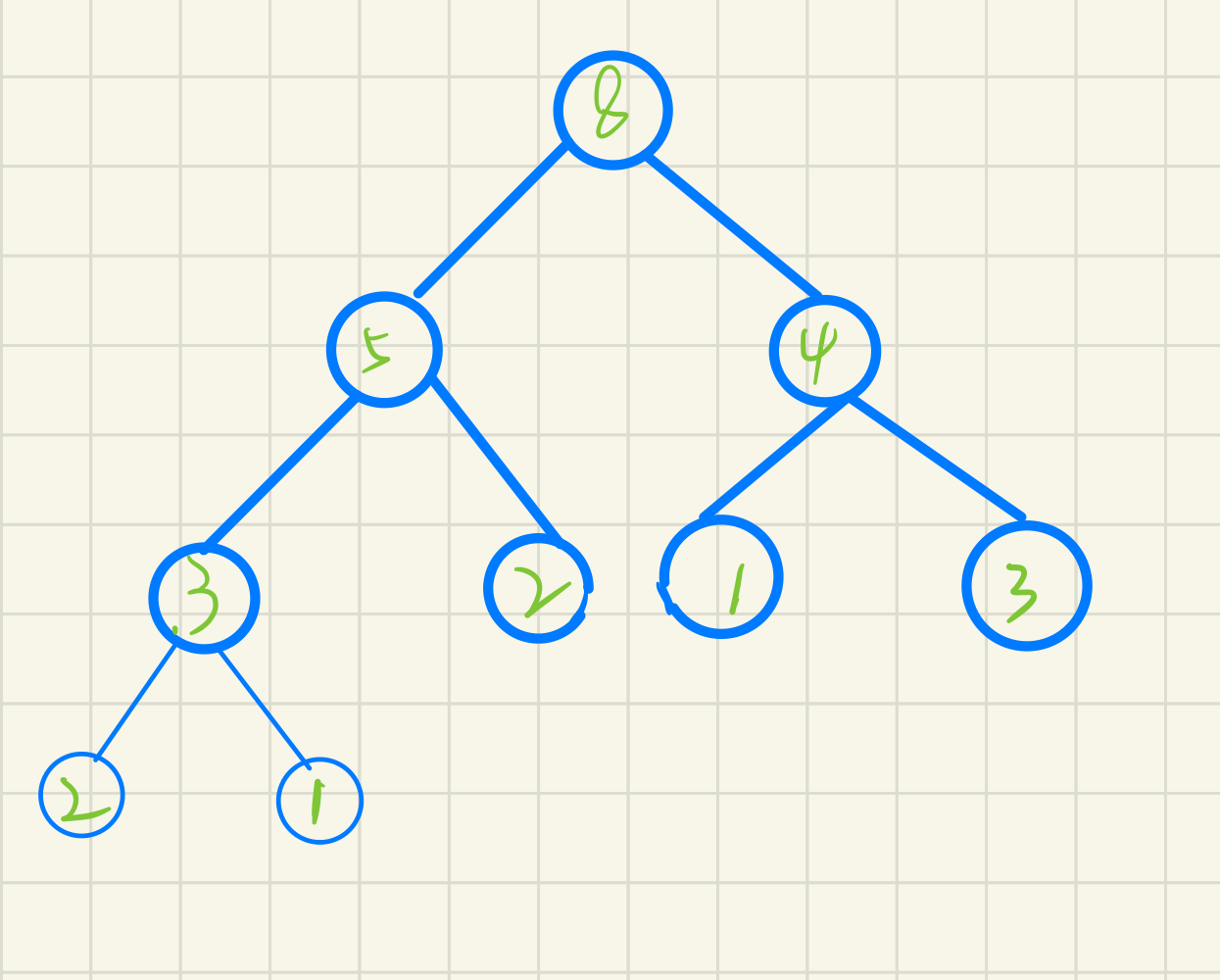
The parent node of the binary tree is always smaller than its child node, which is called small heap
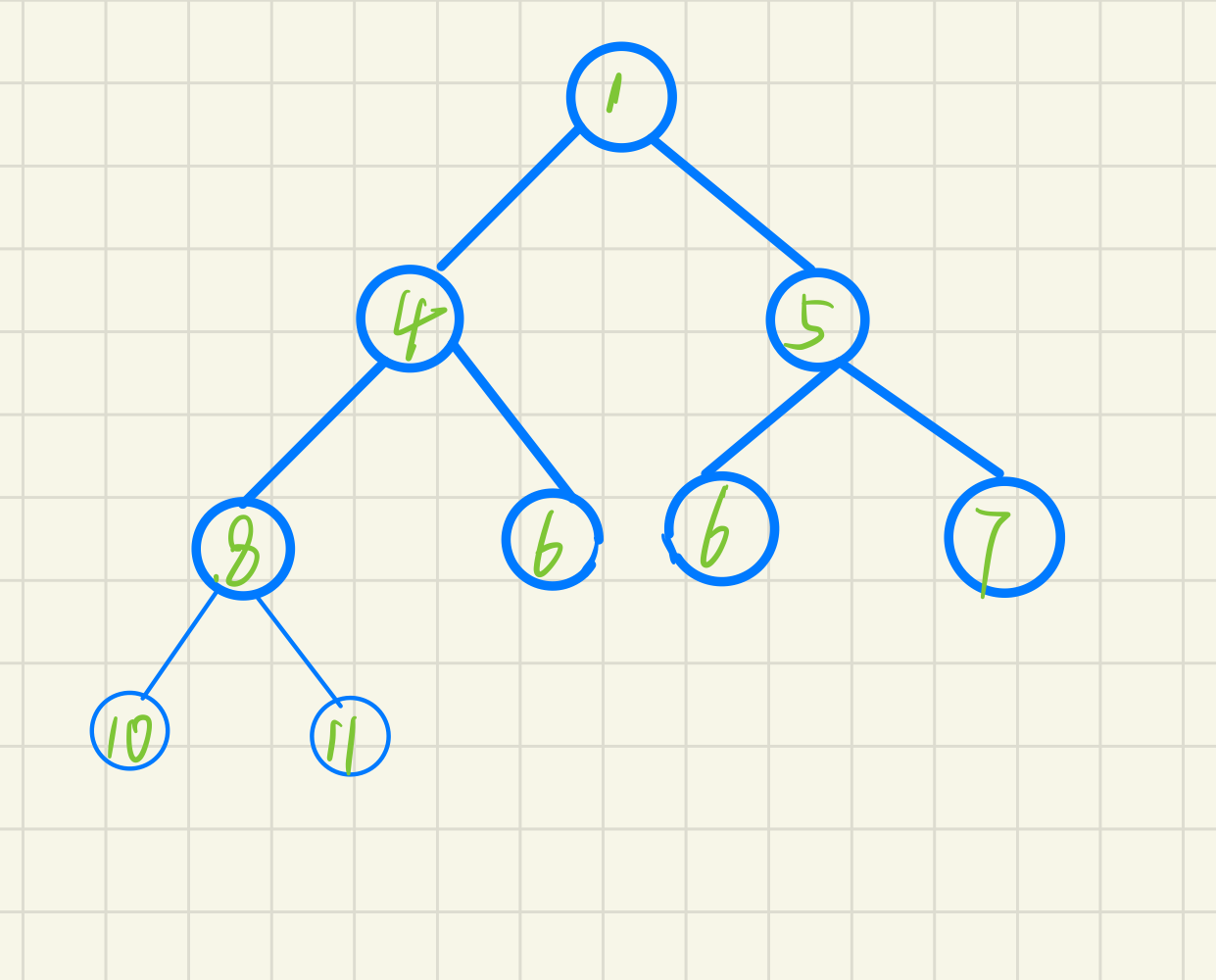
Nature of heap
The value of a node in the heap is always not greater than or less than the value of its parent node;
Heap is always a complete binary tree.
Implementation of heap
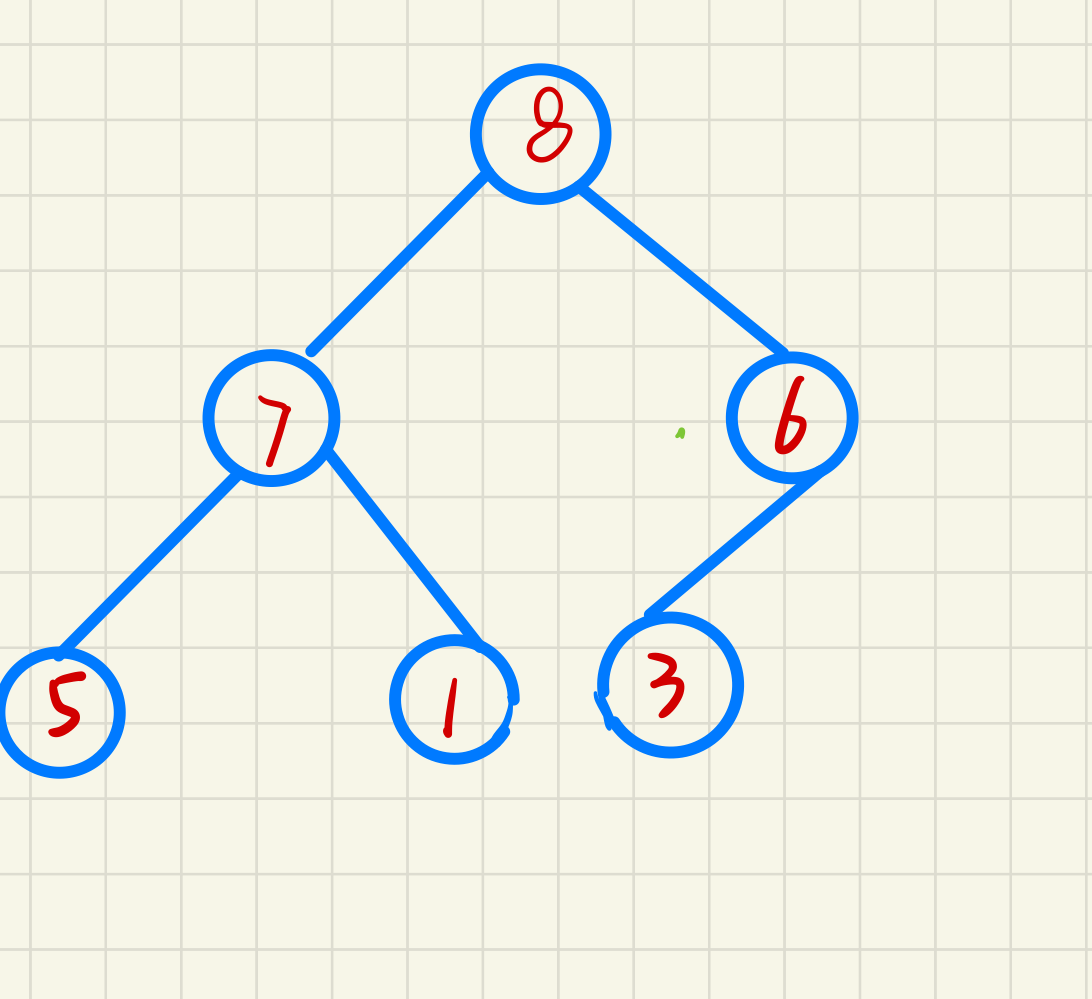
Problem introduction (taking small heap as an example)
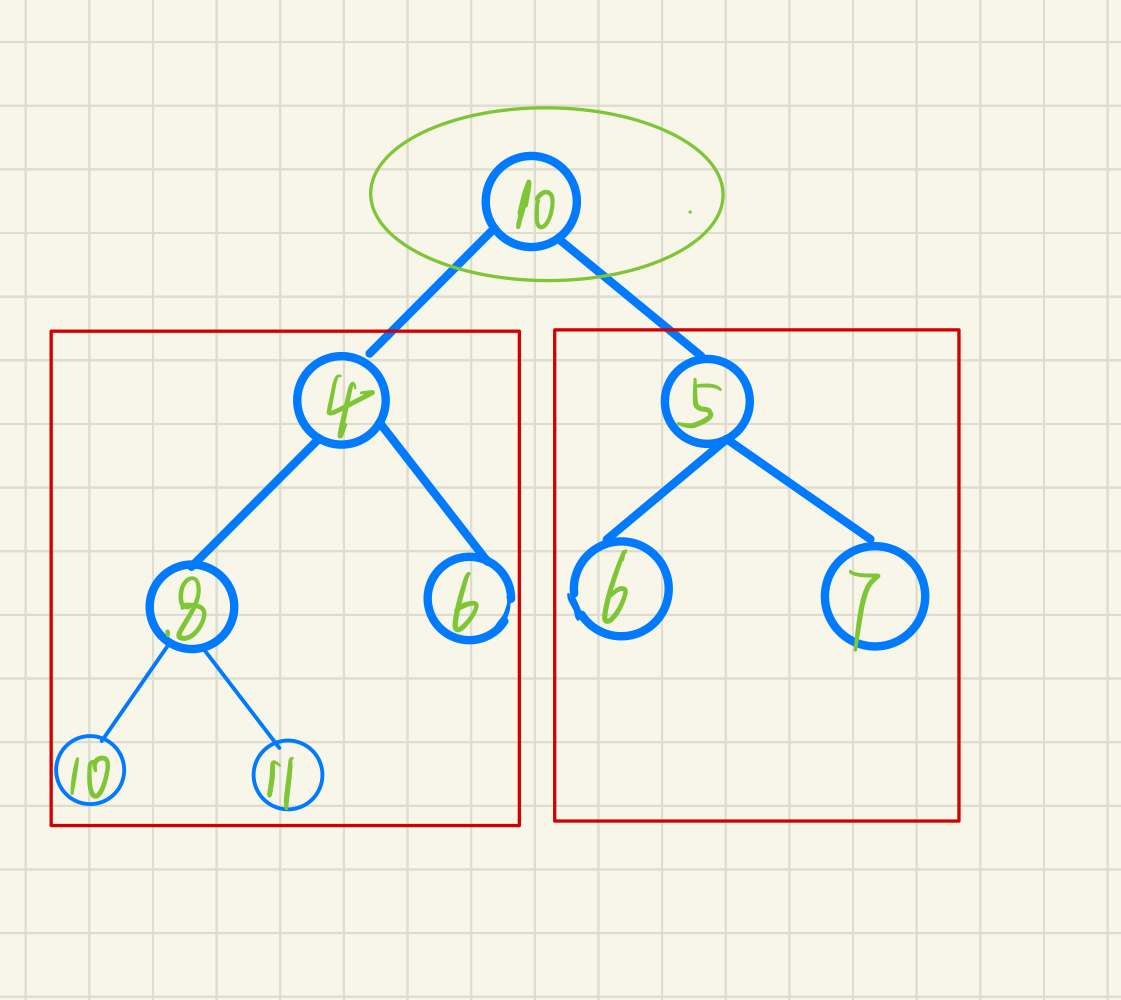
As shown in the figure above: the red part already conforms to the characteristics of small heap, so how should we adjust the nodes of the green part to make the whole binary tree a small heap?
We only need to do the following steps:
1. Find the smaller node among the children around the node
2. Exchange these two nodes
3. Perform the same operation on the exchanged part (1.2)
4. Stop until the node has no child nodes
Then the operation steps for the above situation are shown in the figure below:

Adjustment algorithm
For the execution process of the above situation, the bosses summarized an algorithm to realize such a function, that is, the downward adjustment algorithm
Premise: the left and right subtrees can be adjusted only when they are a heap
Therefore, the steps are:
1. Find the penultimate non leaf node and adjust from this node
2. Find the smaller node among the children around the node
3. Exchange these two nodes
4. Perform the same operation on the exchanged part (2.3)
5. A round of adjustment is completed until the node has no child nodes
6. Adjust the previous non leaf node until it stops at the root node
7. The heap built at this time is a small heap
To build a large stack, you only need to change the above smaller to larger each time you swap
Heap creation
For a given array of arbitrary data, it does not conform to the characteristics of heap at first.
Since the left and right subtrees of the root node are not heaps, we can adjust them from the penultimate non leaf node to the root node
e.g int a[] = {1,5,3,8,7,6};
Adjust into a pile
The adjustment process of this array is shown in the following figure:

Every time an element is exchanged, the structure of its sub heap may be destroyed. Therefore, every time an element exchange occurs, it is necessary to call recursively to reconstruct the structure of the heap.
Time complexity of reactor building
Since the heap is a complete binary tree, and the full binary tree is also a special complete binary tree, the full binary tree is used to solve the time complexity (the time complexity is an approximate value in this book, and more nodes will not affect the final result)
Let the height of the tree be h
Layer 1, 2 ^ 0 nodes, need to move down layer h-1
Layer 2, 2 ^ 1 nodes, need to move down layer h-2
Layer 3, 2 ^ 2 nodes, need to move down layer h-3
Layer 4, 2 ^ 3 nodes, need to move down layer h-4
...
Layer h-1, 2^(h-2) nodes, need to move layer 1 downward
Therefore, the total number of steps required to move nodes is:

Heap insertion
Put the data to be inserted at the end of the array, and then adjust the algorithm upward until the heap is satisfied
e.g insert data 100 into the example during heap building
The new array is {8,7,6,5,1,3100}
The corresponding adjustment process is shown in the figure below
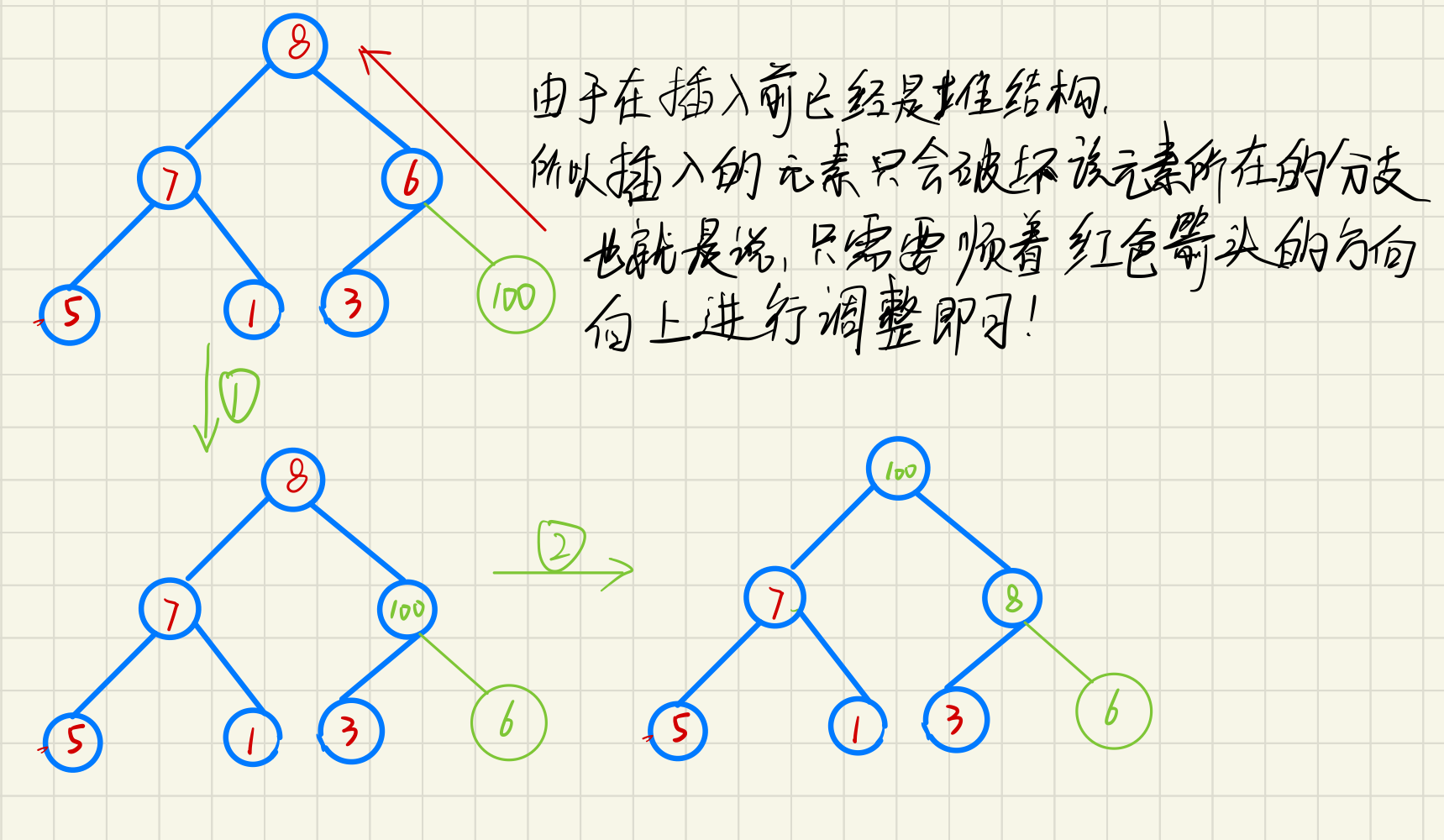
Deletion of heap
Deleting the heap is to delete the data at the top of the heap, exchange the data at the top of the heap with the last data, delete the last element, and then adjust the algorithm downward
e.g delete the top element 100 in the newly built pile
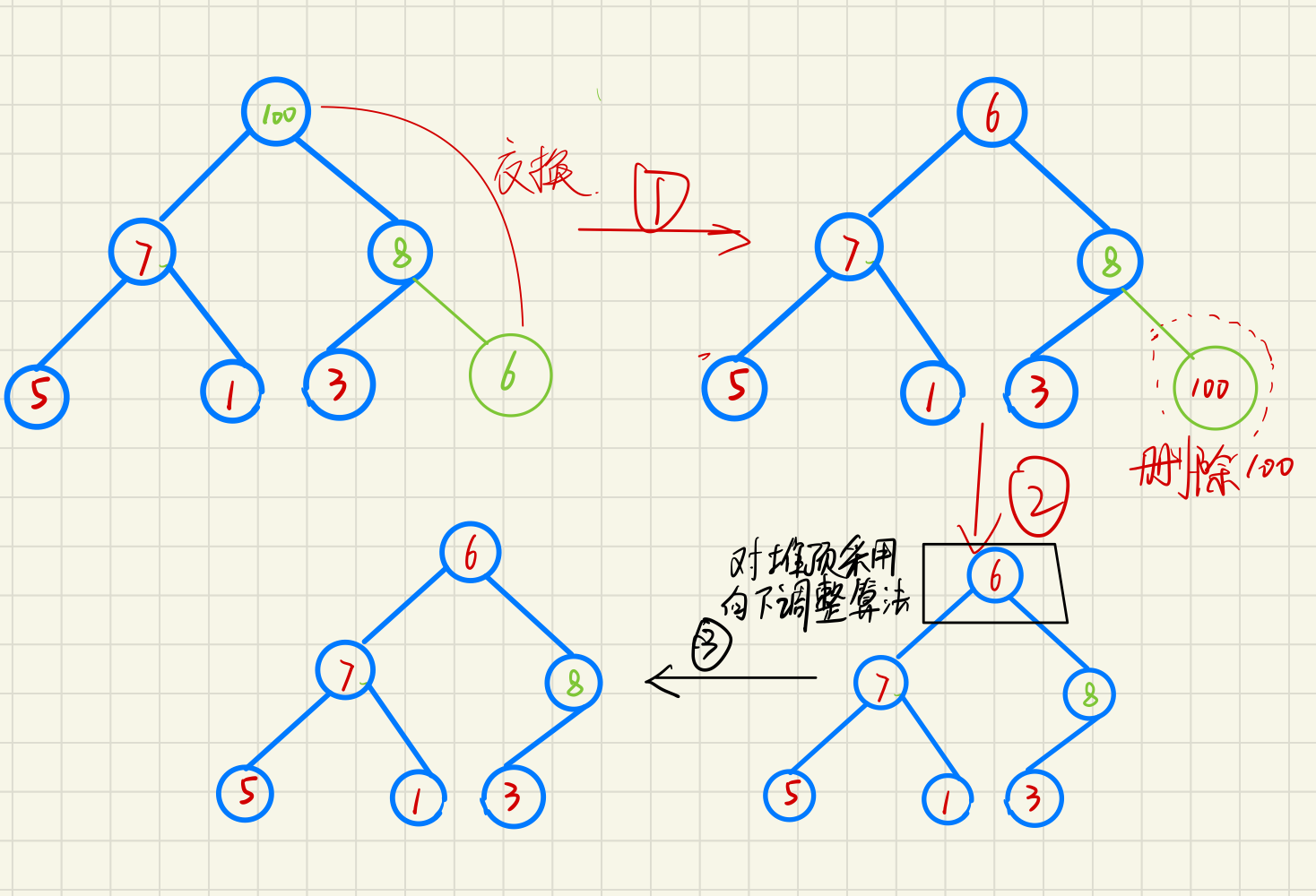
Code implementation of heap
heap.h
Some basic operations of heap are declared
#pragma once
#include <stdio.h>
#include <windows.h>
typedef int HPDataType;
//Defines a function pointer type with a return value of int and two int type parameters
typedef int(*Com) (HPDataType, HPDataType);
typedef struct Heap
{
HPDataType* arr;
int size;
int capacity;
Com Compare;
}Heap;
// Heap construction
extern void HeapCreat(Heap* hp, HPDataType* a, int n,Com com);
// Heap destruction
extern void HeapDestory(Heap* hp);
// Take the data from the top of the heap
extern HPDataType HeapTop(Heap* hp);
//Number of data in the heap
extern int HeapsSize(Heap* hp);
// Empty judgment of heap
extern int HeapEmpty(Heap* hp);
// Heap insertion
extern void HeapPush(Heap* hp, HPDataType x);
// Deletion of heap
extern void HeapPop(Heap* hp);
extern void HeapTest();
heap.c
#include "heap.h"
#include <malloc.h>
#include <assert.h>
static void Swap(HPDataType* xp, HPDataType* yp)
{
HPDataType temp = *xp;
*xp = *yp;
*yp = temp;
}
static void AdjustDown(Heap* hp, int parent)
{
assert(hp);
//1.child marks the left and right children as smaller, and the left child of the default parent node is the smaller of the left and right children
int child = 2 * parent + 1;
while (child < hp->size)
{
//2. Determine the actual smaller child nodes
if (child + 1 < hp->size && hp->Compare(hp->arr[child+1],hp->arr[child]))
{
child += 1;
}
//3. Compare the smaller child node with the parent node to determine whether it needs to be exchanged
if (hp->Compare(hp->arr[child] , hp->arr[parent]))
{
Swap(&hp->arr[child], &hp->arr[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
return;
}
}
}
// Heap construction
void HeapCreat(Heap* hp, HPDataType* a, int n,Com com)
{
assert(a);
assert(hp);
//1. Open up space
hp->arr = (HPDataType*)malloc(sizeof(HPDataType)*n);
if (NULL == hp->arr)
{
assert(0);
return;
}
//2. The space is successfully opened and the new space is initialized
for (int i = 0; i < n; i++)
{
hp->arr[i] = a[i];
}
hp->capacity = n;
hp->size = n;
hp->Compare = com;
//3. Use the downward adjustment method to build the heap
int parent = (n - 2) / 2;
while (parent >= 0)
{
AdjustDown(hp, parent);
parent--;
}
}
// Heap destruction
void HeapDestory(Heap* hp)
{
assert(hp);
if (hp->arr)
{
free(hp->arr);
hp->arr = NULL;
hp->capacity = hp->size = 0;
}
}
// Return value of empty heap: 1 empty 0 is not empty
int HeapEmpty(Heap* hp)
{
assert(hp);
return hp->size == 0? 1:0;
}
// Take the data from the top of the heap
HPDataType HeapTop(Heap* hp)
{
assert(hp);
if (!HeapEmpty(hp))
{
return hp->arr[0];
}
else
{
printf("The heap is empty! The return value is-1\n");
}
return -1;
}
//Or the number of elements in the heap
int HeapsSize(Heap* hp)
{
assert(hp);
return hp->size;
}
// Deletion of heap
void HeapPop(Heap* hp)
{
assert(hp);
//1. Exchange the top element of the heap with the last element of the heap
Swap(&hp->arr[0], &hp->arr[hp->size - 1]);
//2. For hp size-1, control the number of effective elements
hp->size--;
if (hp->size == 0)
{
free(hp->arr);
hp->arr = NULL;
hp->capacity = 0;
}
//3. Adjust the new heap top element downward
AdjustDown(hp,0);
}
//Expansion function
static void HeapExpand(Heap* hp)
{
int newCapacity = hp->capacity * 2;
//1. Open up new space
HPDataType *tmp = (HPDataType*)malloc(sizeof(HPDataType)*newCapacity);
if (NULL == tmp)
{
assert(0);
return;
}
//2. Copy the contents of the old space to the new space
memcpy(tmp, hp->arr, sizeof(HPDataType)*hp->capacity);
//3. Release old space
free(hp->arr);
hp->arr = tmp;
hp->capacity = newCapacity;
}
//Upward adjustment
static void AdjustUp(Heap* hp)
{
int child = hp->size - 1;
int parent = (child - 1) / 2;
while (child > 0)
{
if (hp->Compare(hp->arr[child] , hp->arr[parent]))
{
Swap(&hp->arr[parent], &hp->arr[child]);
child = parent;
parent = (child - 1) / 2;
}
else
{
return;
}
}
}
// Heap insertion
void HeapPush(Heap* hp, HPDataType x)
{
assert(hp);
//1. Judge whether to insert
if (hp->size == hp->capacity)
{
//Cannot insert, expand first
HeapExpand(hp);
}
//2. Perform the insertion operation
hp->arr[hp->size] = x;
hp->size++;
AdjustUp(hp);
}
/
static int Less(HPDataType left,HPDataType right)
{
return left < right;
}
static int Greater(HPDataType left, HPDataType right)
{
return left > right;
}
void HeapTest()
{
Heap hp;
HPDataType array[] = { 16, 72, 31, 23, 94, 53 };
printf("Initialize heap\n");
HeapCreat(&hp, array, sizeof(array) / sizeof(array[0]), Greater);
printf("Heap top element:%d\n", HeapTop(&hp));
printf("Number of valid elements in the heap:%d\n",HeapsSize(&hp));
printf("After inserting a new element\n");
HeapPush(&hp, 1000);
printf("Heap top element:%d\n", HeapTop(&hp));
printf("Number of valid elements in the heap:%d\n", HeapsSize(&hp));
printf("After deleting the heap top element\n");
HeapPop(&hp);
printf("Heap top element:%d\n", HeapTop(&hp));
printf("Number of valid elements in the heap:%d\n", HeapsSize(&hp));
HeapDestory(&hp);
}
}
main.c
#include "heap.h"
int main()
{
HeapTest();
system("pause");
return 0;
}
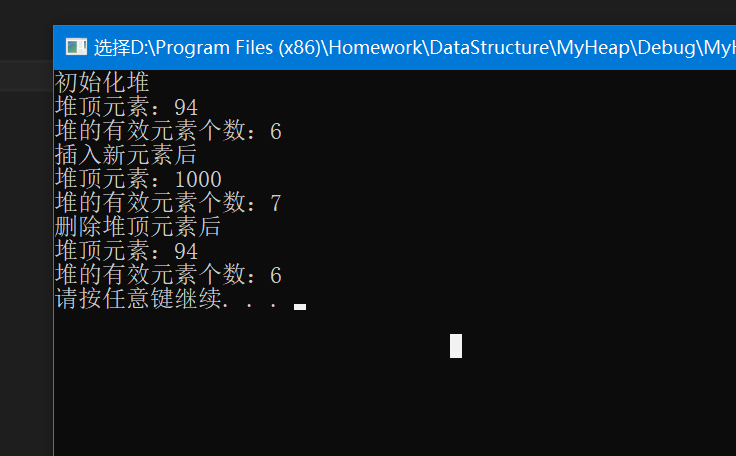
See the source code for relevant operations of heap Pile!
Application of heap
Heap sort
As the name suggests: it is to sort the data by using the idea of heap
It is mainly divided into two steps:
1. Pile building
Ascending order: build a pile
Descending order: build small piles
2. Sort by using the idea of heap deletion
Using downward adjustment algorithm
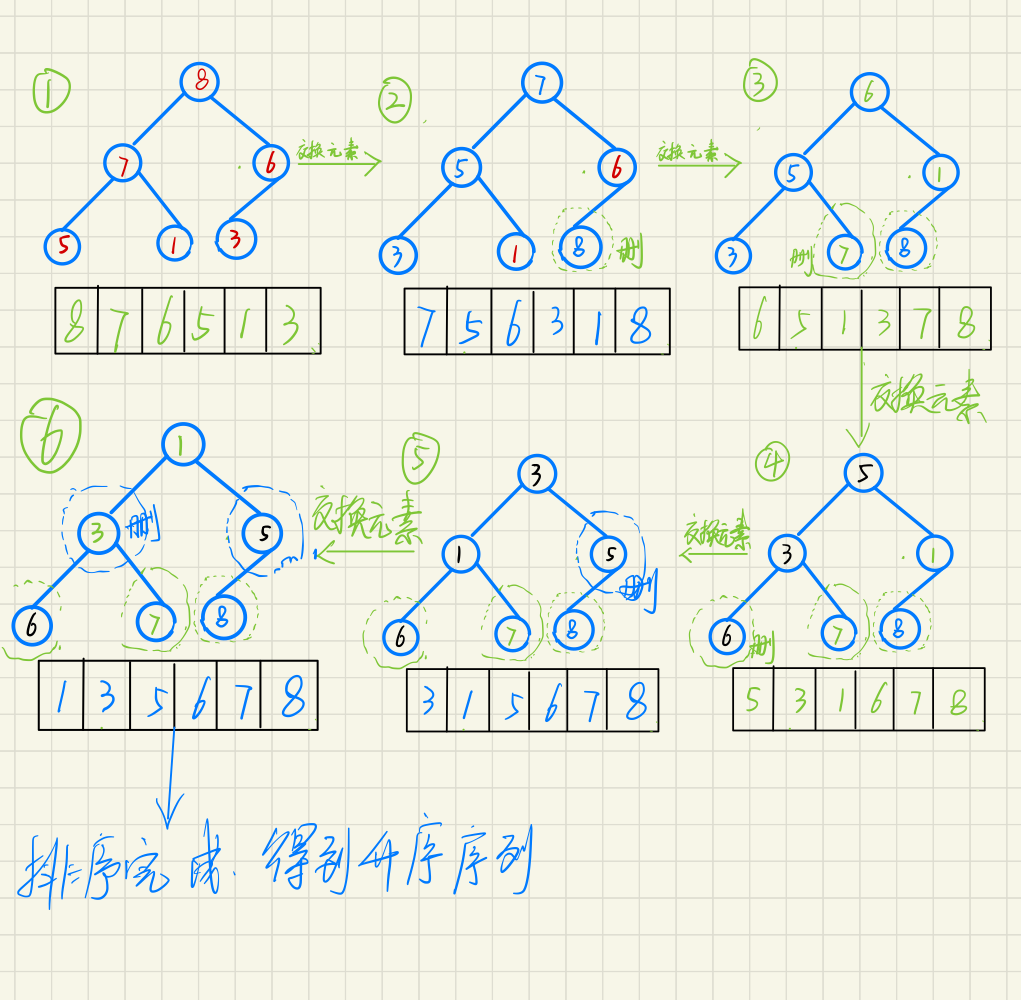
e.g arrange the array {8,7,6,5,1,3} in ascending order
First of all, ascending order needs to be established
Second: delete the structure
The main process is as follows
Implementation code
#include "heap.h"
static void Swap(int* xp,int* yp)
{
int temp = *xp;
*xp = *yp;
*yp = temp;
}
static void AdjustHeap(int* array, int parent, int size)
{
//Use child to mark the parent node
//Since the heap is a complete binary tree, for any parent node,
//It must have left children, but not right children,
//So let the child mark its left child first
int child = parent * 2 + 1;
//Left child exists
if (child < size)
{
//The right child exists, and the right child is smaller than the left child
if (child + 1 < size && array[child] > array[child + 1])
{
//Child relabel right child
child += 1;
}
if (array[parent]>array[child])
{
Swap(&array[parent], &array[child]);
}
else
{
return;
}
}
}
void HeapSort(int *array, int size)
{
//1. Find the first non leaf node
int parent = (size - 1 - 1) / 2;
//2. Start from this node and arrange it by downward adjustment
//3. End until the first element of the array is arranged
while (parent >= 0)
{
AdjustHeap(array, parent, size);
parent--;
}
}
void testHeap()
{
int array[] = { 16, 72, 31, 23, 94, 53 };
int size = sizeof(array) / sizeof(array[0]);
printf("Before:\n");
for (int i = 0; i < size; i++)
{
printf("%d ",array[i]);
}
printf("\n");
HeapSort(array, size);
printf("After:\n");
for (int i = 0; i < size; i++)
{
printf("%d ", array[i]);
}
printf("\n");
}
See source code Heap sort
Top-K problem
Find the first K largest or smallest elements in the data combination. Generally, the amount of data is relatively large.
For example, the top 10 professional enterprises, the world's top 500 enterprises, the rich list, etc
The simplest and direct way to solve the Top-K problem is sorting. However, if the amount of data is very large, sorting is not desirable (maybe the data can not be loaded into memory at one time). The best way is to use heap. The basic idea is as follows
- Use the first k elements in the data set to build the heap
Build a small heap for the first k largest elements
The first k smallest elements - Compare the remaining N-k elements with the heap top elements in turn. If they are not satisfied, replace the heap top elements, and then readjust them to the heap
- After comparing the remaining N-k elements with the top elements in turn, the remaining k elements in the heap are the first k smallest or largest elements.
Reference codes are as follows:
void PrintTopK(int* a, int n, int k)
{
Heap hp;
//Find the first k smallest and build a pile
//HeapCreat(&hp, a, k, Greater);
//Find the first k largest and build a small heap
HeapCreat(&hp, a, k, Less);
for (int i = k; i < n; i++)
{
if (a[i]>HeapTop(&hp))
{
//Delete heap top element
HeapPop(&hp);
//Insert element a[i] into the heap
HeapPush(&hp, a[i]);
}
}
for (int i = 0; i < k; i++)
{
printf("%d ",HeapTop(&hp));
HeapPop(&hp);
}
printf("\n");
}
void TestTopk()
{
int n = 10000;
int* a = (int*)malloc(sizeof(int)*n);
srand(time(0));
//10000 numbers are randomly generated and stored in the array to ensure that the elements are less than 1000000
for (int i = 0; i < n; ++i)
{
a[i] = rand() % 1000000;
}
//Determine the 10 largest numbers
a[5] = 1000000 + 1;
a[1231] = 1000000 + 2;
a[531] = 1000000 + 3;
a[5121] = 1000000 + 4;
a[115] = 1000000 + 5;
a[2335] = 1000000 + 6;
a[9999] = 1000000 + 7;
a[76] = 1000000 + 8;
a[423] = 1000000 + 9;
a[3144] = 1000000 + 10;
PrintTopK(a, n, 10);
}

See source code Top-K
Chain structure and implementation of binary tree
Four traversal methods of binary tree
Preamble
First access the root node, then the left subtree, and then the right subtree
Root left and right
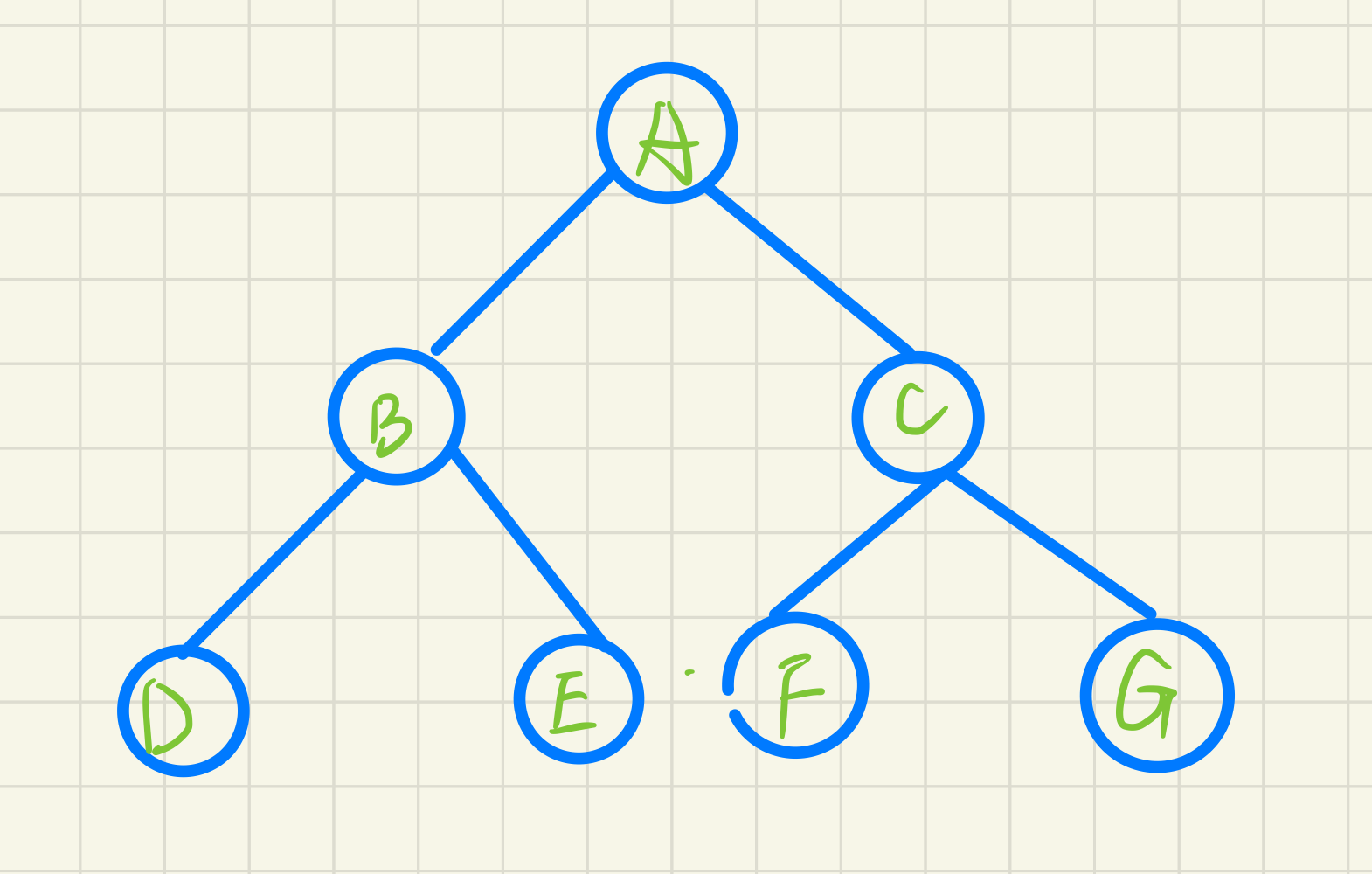
e.g for the binary tree in the following figure, the access sequence is ABDECFG
Middle order
First access the left subtree, then the root node, and then the right subtree
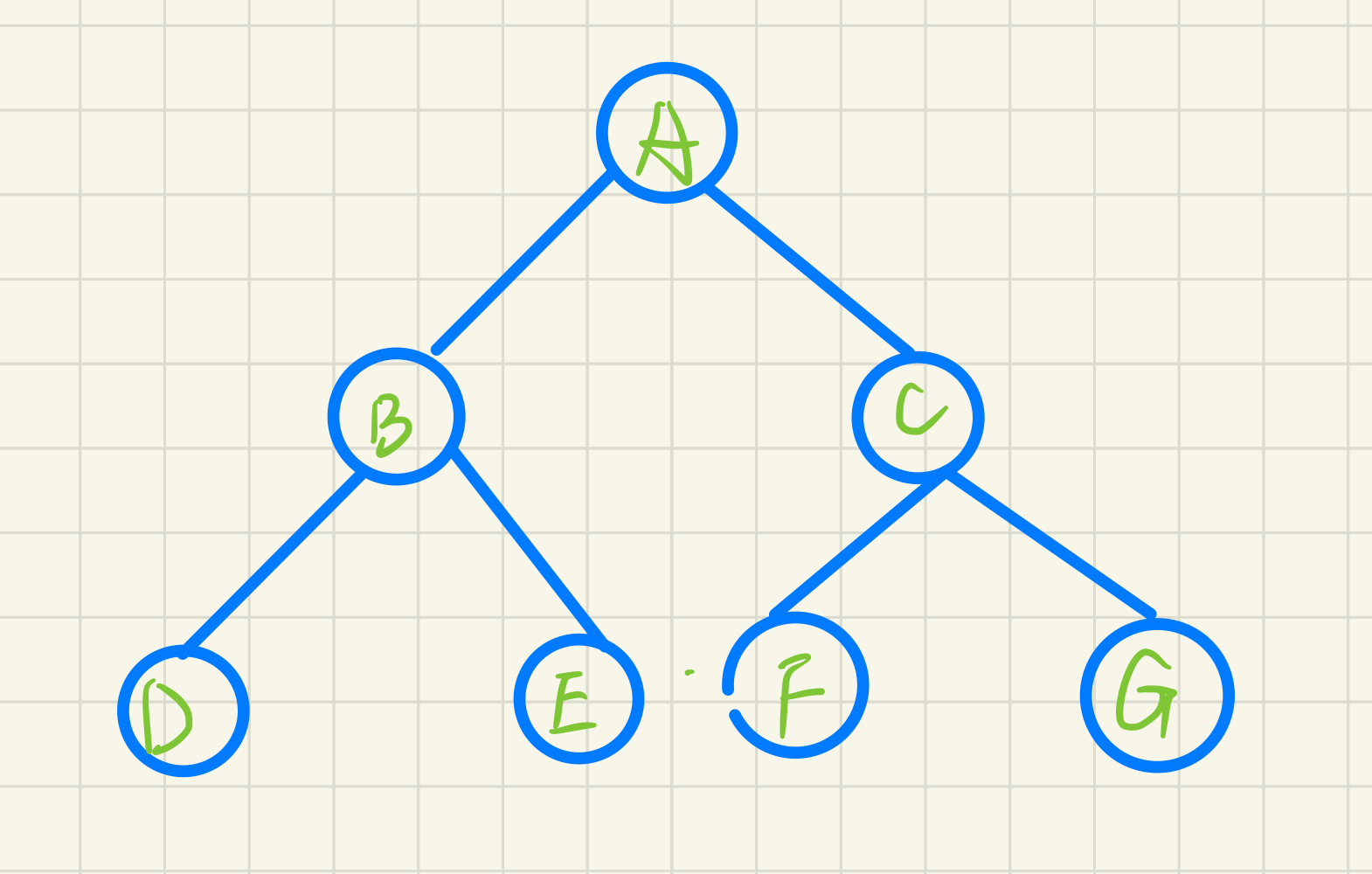
Left root right
e.g for the binary tree in the following figure, the access sequence is: DBEAFCG
Post order
First access the left subtree, then the subtree, and finally the root node
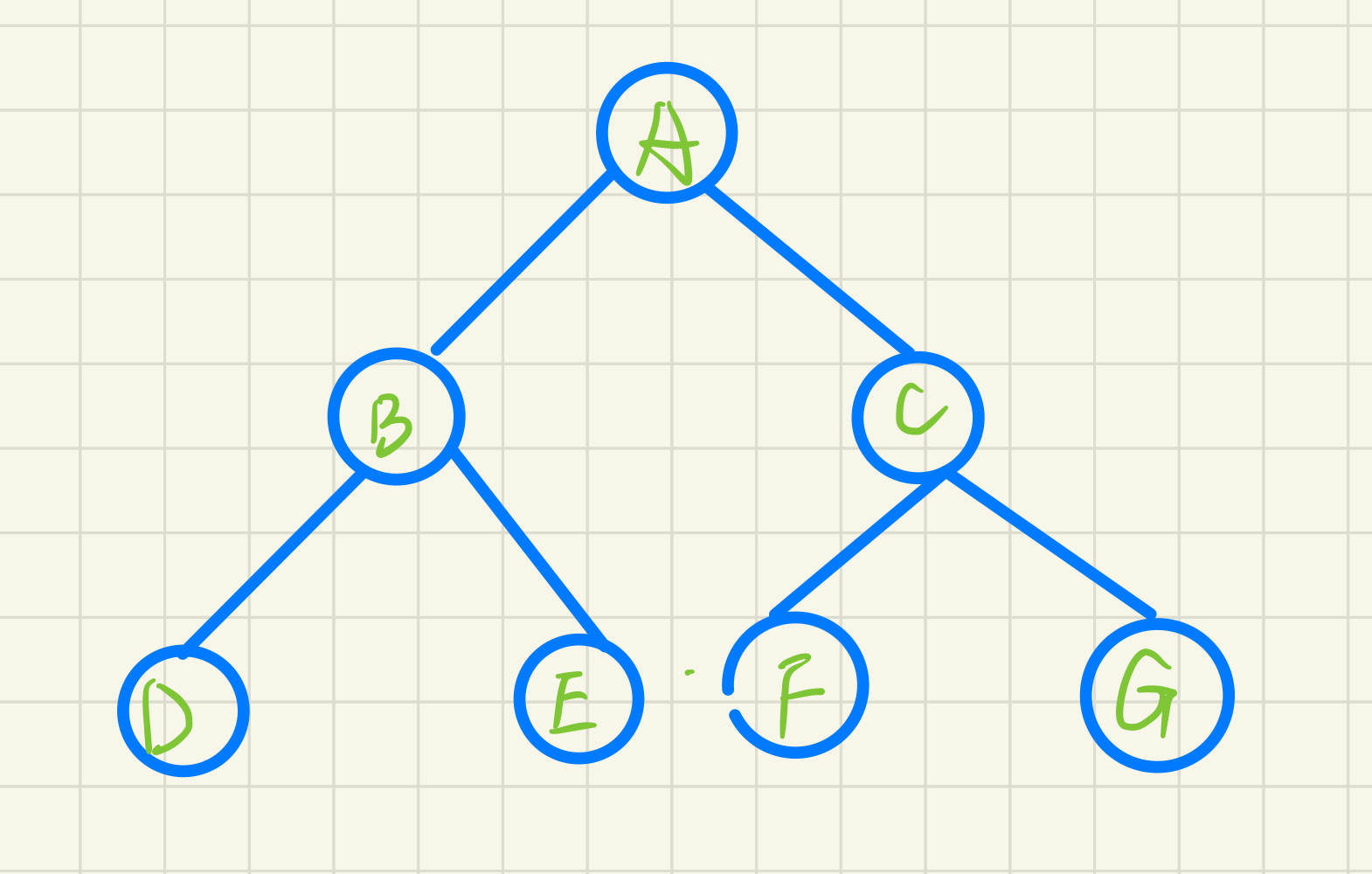
Left and right root
e.g for the binary tree in the following figure, the access sequence is DEBFGCA
sequence
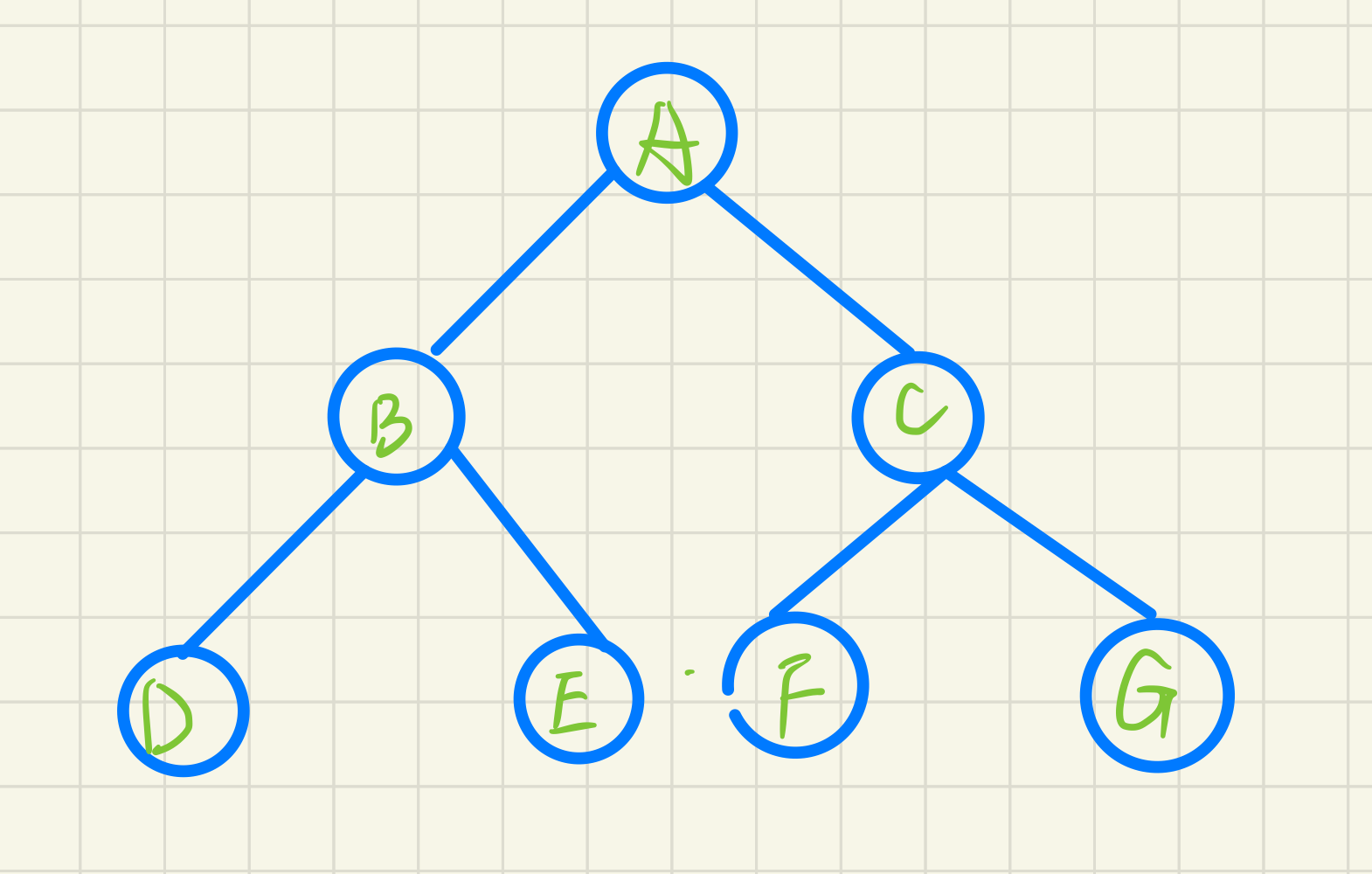
The binary tree is regarded as a tree with layers as units, and each node of the tree is accessed in the way of each layer
e.g for the binary tree in the following figure, the access sequence is ABCDEFG
How should the seemingly simplest sequence traversal be implemented?
Suddenly, there seems to be no train of thought. Don't worry, let's smooth our train of thought slowly
First, it needs to traverse by layer, so we can put it in a container, and then take it out of the container
deposit
When placing, it is placed from top to bottom and from left to right. When taking it, take out the first one
See here is not a little thought, first of all, no matter how it is put in, for taking elements, isn't this the characteristic of the queue
Therefore, the sequence traversal of binary tree needs to be realized with the help of queue
Specific steps:
- Queue root node
- When the queue is not empty:
Join the left and right child nodes of the first element of the queue respectively, and then output the first element and out of the queue - When the queue is empty, it indicates that the sequence traversal has ended and the operation is stopped
For example, the sequence traversal process in the above figure is as follows:

Creation of binary tree (emphasis)
How to create a binary tree?
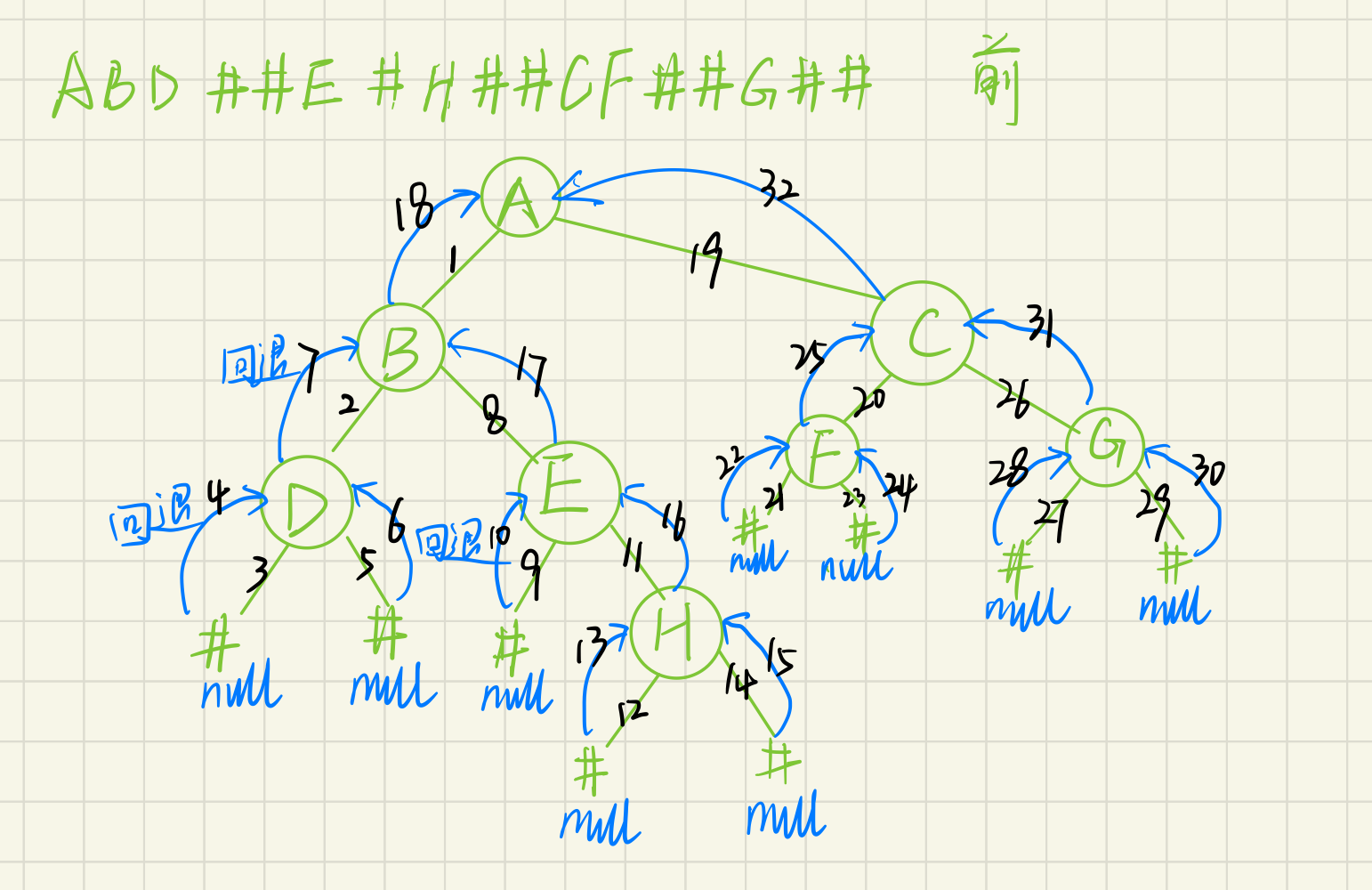
Now let's assume that the binary tree is created in the previous order
The user needs to give an array. The array stores the data field of each node. There should also be some invalid elements in this array to indicate that the left and right children of the node do not exist
The specific establishment steps are as follows:
1. Allocate space for the root node and create the root node
2. Recursively create the left and right subtrees of the root node
3. When an invalid value is encountered during recursion, it indicates that the node has no left subtree or right subtree. At this time, it should fall back to the previous layer
5. Traverse the entire array until the array traversal is completed, and the binary tree is created
e.g: the user input array is "ABD##E#H##CF##G##", where # is an invalid element, the corresponding binary tree creation process is as follows:
// The binary tree is constructed through the array "ABD##E#H##CF##G##" traversed in the previous order
BTNode* BinaryTreeCreate(BTDataType* array, int size, int* index)
{
BTNode* root = NULL;
if (*index < size && array[*index] != ' ')
{
//Create root node
root = BuyBTNode(array[*index]);
//Create left subtree and right subtree recursively
++(*index);
root->left = BinaryTreeCreate(array, size, index);
++(*index);
root->right = BinaryTreeCreate(array, size, index);
}
return root;
}
Note the third parameter in the function:
It represents the subscript of the element to be manipulated in the array. The question is why does it use a pointer? Can't you transfer the value directly?
The reasons are as follows:
First of all, we create a binary tree through recursion. Recursion is a process in which a function calls itself.
Since it is a function call, the formal parameter is a temporary copy of the argument. It is created at the beginning of function execution and automatically destroyed after function execution.
Therefore, if we use the subscript value as the function parameter, the value of the variable outside the function cannot be changed after the function is executed, and our program cannot achieve the expected results.
Therefore, we need to pass in the pointer in order to get the modified result of the variable inside the function.
Binary tree basic operation source code
BinaryTree.h
#pragma once
#include <stdio.h>
#include <windows.h>
typedef char BTDataType;
typedef struct BTNode
{
BTDataType data;
struct BTNode* left;
struct BTNode* right;
}BTNode;
// The binary tree is constructed through the array "ABD##E#H##CF##G##" traversed in the previous order
extern BTNode* BinaryTreeCreate(BTDataType* array, int size, int* index);
// Binary tree destruction
extern void BinaryTreeDestory(BTNode** root);
// Preorder traversal of binary tree
extern void BinaryTreePrevOrder(BTNode* root);
// Order traversal in binary tree
extern void BinaryTreeInOrder(BTNode* root);
// Postorder traversal of binary tree
extern void BinaryTreePostOrder(BTNode* root);
// level traversal
extern void BinaryTreeLevelOrder(BTNode* root);
// Number of binary tree nodes
extern int BinaryTreeSize(BTNode* root);
// Number of leaf nodes of binary tree
extern int BinaryTreeLeafSize(BTNode* root);
// Number of nodes in the k-th layer of binary tree
extern int BinaryTreeLevelKSize(BTNode* root, int k);
// The binary tree looks for a node with a value of x
extern BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// Judge whether the binary tree is a complete binary tree
extern int BinaryTreeComplete(BTNode* root);
extern void BTtest();
BinaryTree.c
#include "Binarytree.h"
#include "queue.h"
#include <assert.h>
static BTNode* BuyBTNode(BTDataType x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (NULL == node)
{
assert(0);
return NULL;
}
node->data = x;
node->left = node->right = NULL;
return node;
}
// The binary tree is constructed through the array "ABD##E#H##CF##G##" traversed in the previous order
BTNode* BinaryTreeCreate(BTDataType* array, int size, int* index)
{
BTNode* root = NULL;
if (*index < size && array[*index] != ' ')
{
//Create root node
root = BuyBTNode(array[*index]);
//Create left subtree and right subtree recursively
++(*index);
root->left = BinaryTreeCreate(array, size, index);
++(*index);
root->right = BinaryTreeCreate(array, size, index);
}
return root;
}
// Binary tree destruction
void BinaryTreeDestory(BTNode** root)
{
assert(root);
if (*root)
{
BinaryTreeDestory(&(*root)->left);
BinaryTreeDestory(&(*root)->right);
free(*root);
*root = NULL;
}
}
// Preorder traversal of binary tree
void BinaryTreePrevOrder(BTNode* root)
{
if (NULL == root)
{
return;
}
printf("%c ", root->data);
BinaryTreePrevOrder(root->left);
BinaryTreePrevOrder(root->right);
}
// Order traversal in binary tree
void BinaryTreeInOrder(BTNode* root)
{
if (NULL == root)
{
return;
}
BinaryTreeInOrder(root->left);
printf("%c ", root->data);
BinaryTreeInOrder(root->right);
}
// Postorder traversal of binary tree
void BinaryTreePostOrder(BTNode* root)
{
if (NULL == root)
{
return;
}
BinaryTreePostOrder(root->left);
BinaryTreePostOrder(root->right);
printf("%c ", root->data);
}
// level traversal
void BinaryTreeLevelOrder(BTNode* root)
{
if (NULL == root)
{
return;
}
//Queue implementation
Queue q;
QueueInit(&q);
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* cur = QueueFront(&q);
printf("%c ",cur->data );
QueuePop(&q);
if (cur->left)
{
QueuePush(&q, cur->left);
}
if (cur->right)
{
QueuePush(&q, cur->right);
}
}
QueueDestroy(&q);
}
// Number of binary tree nodes
int BinaryTreeSize(BTNode* root)
{
if (NULL == root)
{
return 0;
}
return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}
// Number of leaf nodes of binary tree
int BinaryTreeLeafSize(BTNode* root)
{
if (NULL == root)
{
return 0;
}
if (NULL == root->left && NULL == root->right)
{
return 1;
}
return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
// Number of nodes in the k-th layer of binary tree
int BinaryTreeLevelKSize(BTNode* root, int k)
{
if (NULL == root || k < 1)
{
return 0;
}
if (k == 1)
{
return 1;
}
return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}
// The binary tree looks for a node with a value of x
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
BTNode* ret = NULL;
if (NULL == root)
{
return NULL;
}
if (x == root->data)
{
return root;
}
if (ret = BinaryTreeFind(root->left, x))
{
return ret;
}
return BinaryTreeFind(root->right, x);
}
// Judge whether the binary tree is a complete binary tree 1 --- is a complete binary tree 0 --- is not a complete binary tree
int BinaryTreeComplete(BTNode* root)
{
//Using the idea of sequence traversal and relying on queue to realize judgment
//An empty tree is also a complete binary tree
if (NULL == root)
{
return 1;
}
Queue q;
QueueInit(&q);
BTNode* cur = root;
//1. Queue the nodes of each layer (empty nodes are queued according to NULL)
QueuePush(&q, cur);
while ((cur = QueueFront(&q)) != NULL)
{
QueuePop(&q);
QueuePush(&q,cur->left);
QueuePush(&q,cur->right);
}
//2. Judge the queue at this time: if all nodes in the queue are NULL, it means that it is a complete binary tree, otherwise it is not a complete binary tree
while (!QueueEmpty(&q))
{
cur = QueueFront(&q);
if (cur != NULL)
{
return 0;
}
QueuePop(&q);
}
return 1;
}
void BTtest()
{
BTNode* root = NULL;
BTDataType array[] = "ABD E H CF G ";
int index = 0;
root = BinaryTreeCreate(array,sizeof(array)/sizeof(array[0]),&index);
//Preamble
BinaryTreePrevOrder(root);
printf("\n");
//Middle order
BinaryTreeInOrder(root);
printf("\n");
//Post order
BinaryTreePostOrder(root);
printf("\n");
//sequence
BinaryTreeLevelOrder(root);
printf("\n");
printf("The number of binary tree nodes is:%d\n", BinaryTreeSize(root));
printf("The number of leaf nodes of binary tree is:%d\n", BinaryTreeLeafSize(root));
int k = 4;
printf("Binary tree %d The number of nodes in the layer is %d\n",k, BinaryTreeLevelKSize(root,k));
BTNode* cur = BinaryTreeFind(root,'D');
if (cur)
{
printf("existence\n");
}
else
{
printf("non-existent\n");
}
int flag = BinaryTreeComplete(root);
if (flag)
{
printf("The binary tree is a complete binary tree!\n");
}
else
{
printf("The binary tree is not a complete binary tree!\n");
}
}
Specific source code reference BinaryTree