catalogue
1, Time complexity and space complexity
② Asymptotic representation of large O
③ Common time complexity calculation examples
2, Linear list (single linked list and double linked list)
⑤ Gets the effective length of the sequence table
⑦ Judge whether to find the corresponding position of an element. If not, return - 1
⑧ Get the element of pos position and set / update the element of pos position to value
⑨ Delete the keyword key that appears for the first time
② Implementation of linked list
④ Create linked list and print linked list
⑥ head insertion method and tail insertion method
⑦ Find the address of the node at index-1 and insert the element
⑨ Delete all nodes with the value of key
① Implementation of linked list
② Construct nodes and linked lists
③ Print the linked list and calculate the length of the linked list
① Reverse a single linked list
③ Input a linked list and output the penultimate node in the linked list
④ Delete multiple duplicate values in the linked list
⑤ Palindrome structure of linked list
⑦ Enter two linked lists and find their first common node
⑧ Determine whether a linked list has a ring
⑨ Find the first node of a linked list
① Preorder traversal of binary tree
② Order traversal in binary tree
③ Postorder traversal of binary tree
④ Check whether the two trees are the same
⑤ Maximum depth of binary tree
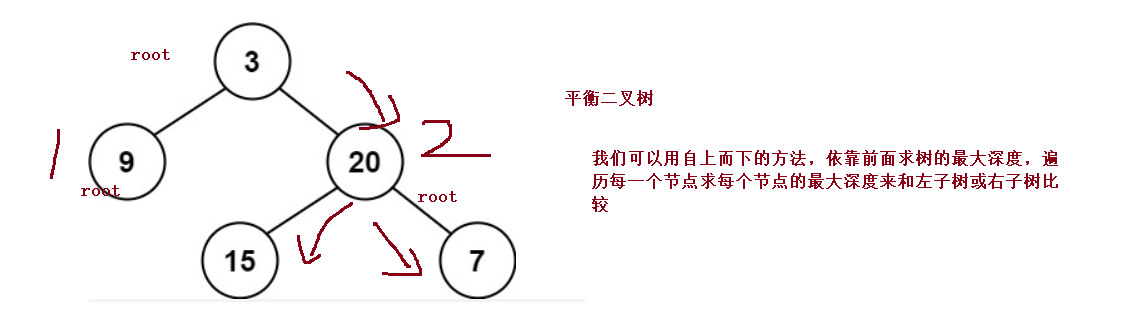
⑦ Judge whether a tree is a balanced binary tree
1. Sequential storage of binary tree
③ Binary tree sequential traversal
② Operation - downward adjustment
③ Pile building (taking pile building as an example)
3. Heap application - priority queue
④ Out of queue (highest priority)
⑤ Return to the first element of the queue (highest priority)
② About map Description of entry
③ Description of common methods of Map
① Description of common methods
preface
As a difficult subject to learn, data structure is also a subject that we as programmers must firmly grasp in the future. We should draw more pictures and write more code in order to gain something. This blog can be used as an entry-level teaching. There will be diagrams and detailed code in it. The summary content represents our personal point of view, There are some data structure contents that are not summarized, but enough to learn as a beginner of data structure, as well as detailed explanations of written test questions of various large factories. The content of this blog is long and it is recommended to collect it. If you think this blog is good, please praise and collect it. It's not easy to make it and don't talk too much nonsense. Let's learn it!!!
1, Time complexity and space complexity
1. Algorithm efficiency
There are two kinds of algorithm efficiency analysis: the first is time efficiency and the second is space efficiency. Time efficiency is called time complexity, and space efficiency is called space complexity. Time complexity mainly measures the running speed of an algorithm, while space complexity mainly measures the additional space required by an algorithm. In the early stage of computer development, the storage capacity of the computer is very small. So I care about the degree of space. However, with the rapid development of computer industry, the storage capacity of computer has reached a high level. Therefore, we no longer need to pay special attention to the spatial complexity of an algorithm.
2. Time complexity
① Concept of time complexity
Definition of time complexity: in computer science, the time complexity of an algorithm is a function that quantitatively describes the running time of the algorithm. In theory, the time spent in the execution of an algorithm cannot be calculated. You can only know when you put your program on the machine and run it. But do we need every algorithm to be tested on the computer? Yes, it can be tested on the computer, but it is very troublesome, so there is the analysis method of time complexity. The time spent by an algorithm is directly proportional to the execution times of the statements in it. The execution times of the basic operations in the algorithm is the time complexity of the algorithm.
② Asymptotic representation of large O
void func1(int N){
int count = 0;
for (int i = 0; i < N ; i++) {
for (int j = 0; j < N ; j++) {
count++;
}
}
for (int k = 0; k < 2 * N ; k++) {
count++;
}
int M = 10;
while ((M--) > 0) {
count++;
}
System.out.println(count);
}Please calculate how many times func1 basic operations have been performed?
Number of basic operations performed by Func1:
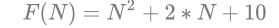
N = 10 F(N) = 130
N = 100 F(N) = 10210
N = 1000 F(N) = 1002010
In fact, when we calculate the time complexity, we do not have to calculate the exact execution times, but only the approximate execution times. Here, we use the asymptotic representation of large O.
Big O notation: a mathematical symbol used to describe the asymptotic behavior of a function.
Derivation of large O-order method:
1. Replace all addition constants in the run time with constant 1.
2. In the modified run times function, only the highest order term is retained.
3. If the highest order term exists and is not 1, the constant multiplied by this item is removed. The result is large O-order.
After using the progressive representation of large O, the time complexity of Func1 is:
O(N^2)
N = 10 F(N) = 100
N = 100 F(N) = 10000
N = 1000 F(N) = 1000000
From the above, we can find that the progressive representation of big O removes those items that have little impact on the results, and succinctly represents the execution times. In addition, the time complexity of some algorithms has the best, average and worst cases:
Worst case: maximum number of runs of any input scale (upper bound)
Average case: expected number of runs of any input scale
Best case: minimum number of runs of any input scale (lower bound)
In practice, we usually focus on the worst-case operation of the algorithm, so the time complexity of searching data in the array is O(N)
③ Common time complexity calculation examples
void func2(int N) {
int count = 0;
for (int k = 0; k < 2 * N ; k++) {
count++;
}
int M = 10;
while ((M--) > 0) {
count++;
}
System.out.println(count);
}
void func3(int N, int M) {
int count = 0;
for (int k = 0; k < M; k++) {
count++;
}
for (int k = 0; k < N ; k++) {
count++;
}
System.out.println(count);
}
void func4(int N) {
int count = 0;
for (int k = 0; k < 100; k++) {
count++;
}
System.out.println(count);
}
void bubbleSort(int[] array) {
for (int end = array.length; end > 0; end--) {
boolean sorted = true;
for (int i = 1; i < end; i++) {
if (array[i -1] > array[i]) {
Swap(array, i - 1, i);
sorted = false;
}
}
if (sorted == true) {
break;
}
}
}
int binarySearch(int[] array, int value) {
int begin = 0;
int end = array.length - 1;
while (begin <= end) {
int mid = begin + ((end-begin) / 2);
if (array[mid] < value)
begin = mid + 1;
else if (array[mid] > value)
end = mid - 1;
else
return mid;
}
return -1;
}
long factorial(int N) {
return N < 2 ? N : factorial(N-1) * N;
}
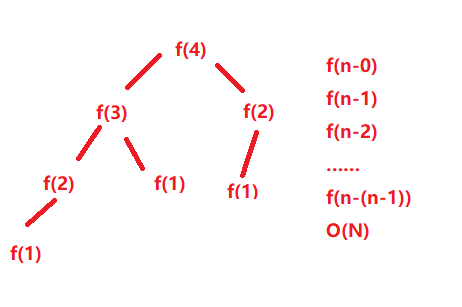
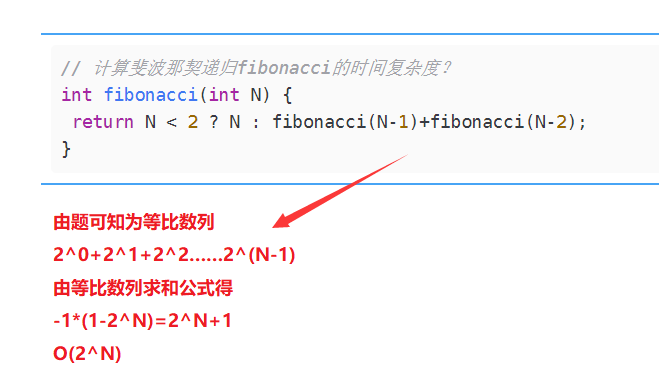
// Computing the time complexity of fibonacci recursive fibonacci?
int fibonacci(int N) {
return N < 2 ? N : fibonacci(N-1)+fibonacci(N-2);
}
3. Spatial complexity
Space complexity is a measure of the amount of storage space temporarily occupied by an algorithm during operation. Space complexity is not how many bytes the program occupies, because it doesn't make much sense, so space complexity is the number of variables. The calculation rules of spatial complexity are basically similar to the practical complexity, and the large O asymptotic representation is also used.
// Calculate the spatial complexity of bubbleSort?
void bubbleSort(int[] array) {
for (int end = array.length; end > 0; end--) {
boolean sorted = true;
for (int i = 1; i < end; i++) {
if (array[i - 1] > array[i]) {
Swap(array, i - 1, i);
sorted = false;
}
}
if (sorted == true) {
break;
}
}
}A constant number of extra spaces are used, so the space complexity is O(1)
// How to calculate the spatial complexity of fibonacci?
int[] fibonacci(int n) {
long[] fibArray = new long[n + 1];
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n ; i++) {
fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
}
return fibArray;
}N spaces are opened up dynamically, and the space complexity is O(N)
// The time complexity of computing Factorial recursive Factorial?
long factorial(int N) {
return N < 2 ? N : factorial(N-1)*N;
}Recursively called N times, opened up N stack frames, and each stack frame uses a constant space. Space complexity is O(N)
2, Linear list (single linked list and double linked list)
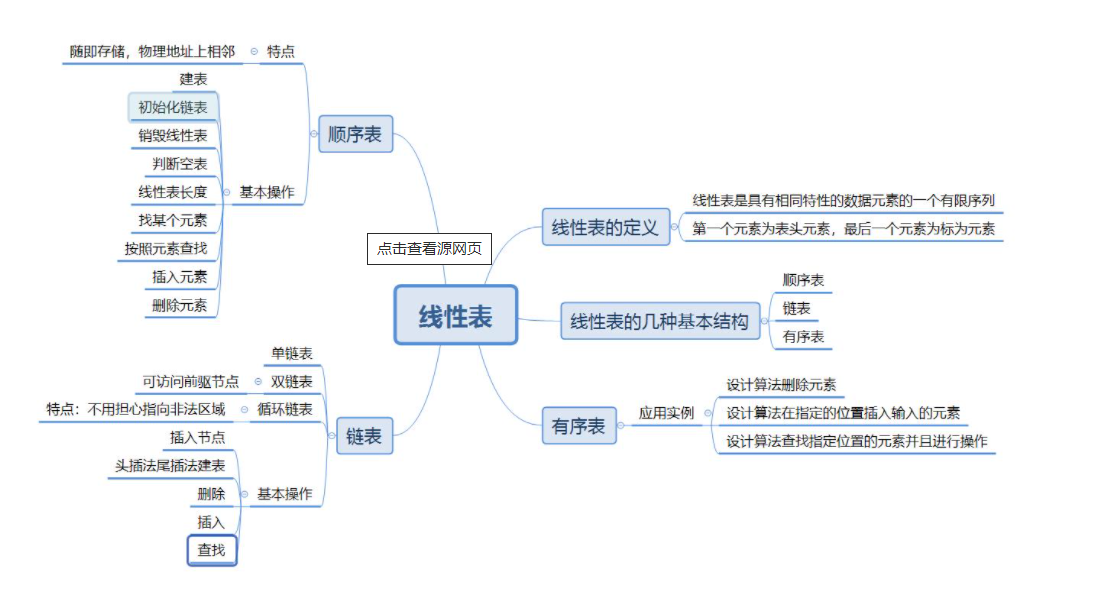
1. Concept
linear list is a finite sequence of n data elements with the same characteristics. linear list is a data structure widely used in practice. Common linear lists include sequential list, linked list, stack, queue and string
A linear table is logically a linear structure, that is, a continuous straight line. However, the physical structure is not necessarily continuous. When the linear table is stored physically, it is usually stored in the form of array and chain structure.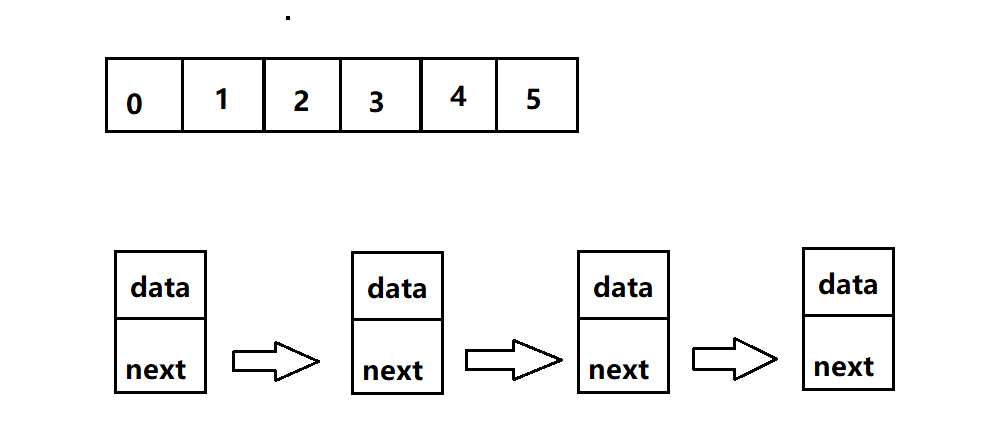
2. Sequence table
① Concept
Sequential table is a linear structure in which data elements are stored in sequence with a storage unit with continuous physical addresses. Generally, array storage is used. Complete the addition, deletion, query and modification of data on the array.
The sequence table can generally be divided into:
Static sequential table: use fixed length array storage.
Dynamic sequential table: use dynamic array storage.
The static sequence table is suitable for scenarios where you know how much data needs to be stored
The fixed length array of static sequence table leads to large N, waste of space and insufficient space
In contrast, the dynamic sequential table is more flexible and dynamically allocates space according to needs.
② Interface implementation
class SeqList {
// Print sequence table
public void display() {
}
// Add new element in pos position
public void add(int pos, int data) {
}
// Determines whether an element is included
public boolean contains(int toFind) {
return true;
}
// Find the location of an element
public int search(int toFind) {
return -1;
}
// Gets the element of the pos location
public int getPos(int pos) {
return -1;
}
// Set the element of pos position to value
public void setPos(int pos, int value) {
}
//Delete the keyword key that appears for the first time
public void remove(int toRemove) {
}
// Get sequence table length
public int size() {
return 0;
}
// Empty sequence table
public void clear() {
}
}③ Create sequence table
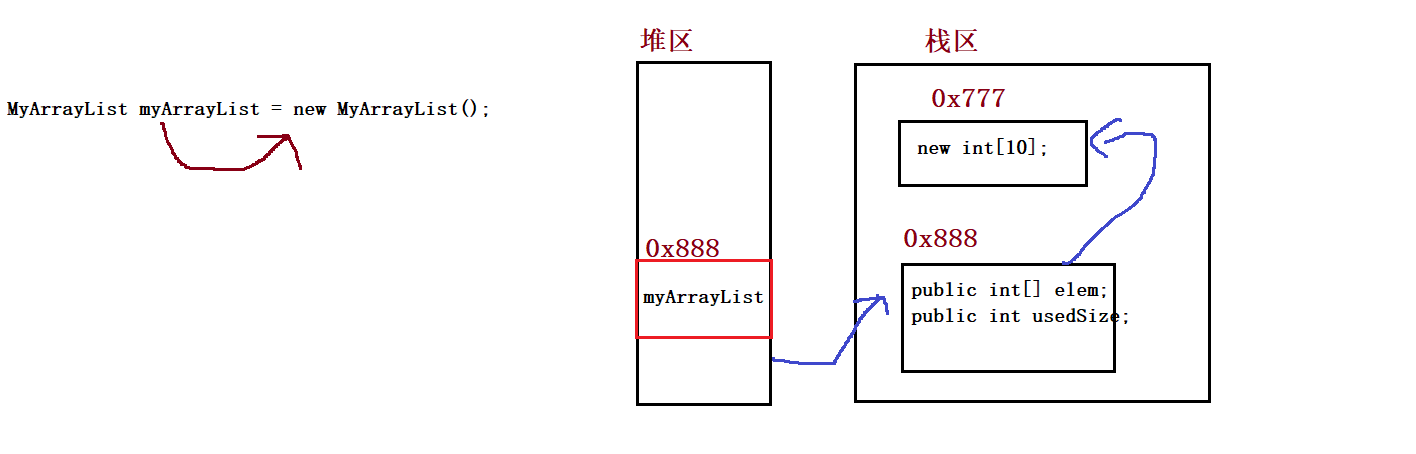
public int[] elem;
public int usedSize;//Number of valid data
public MyArrayList() {
this.elem = new int[10];
}④ Print sequence table
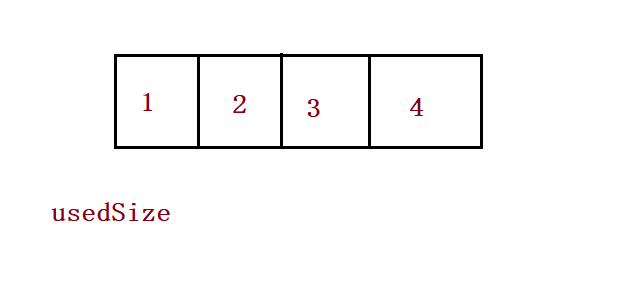
// Print sequence table
public void display() {
for (int i = 0; i < this.usedSize; i++) {
System.out.print(this.elem[i]+" ");
}
System.out.println();
}⑤ Gets the effective length of the sequence table
// Gets the valid data length of the sequence table
public int size() {
return this.usedSize;
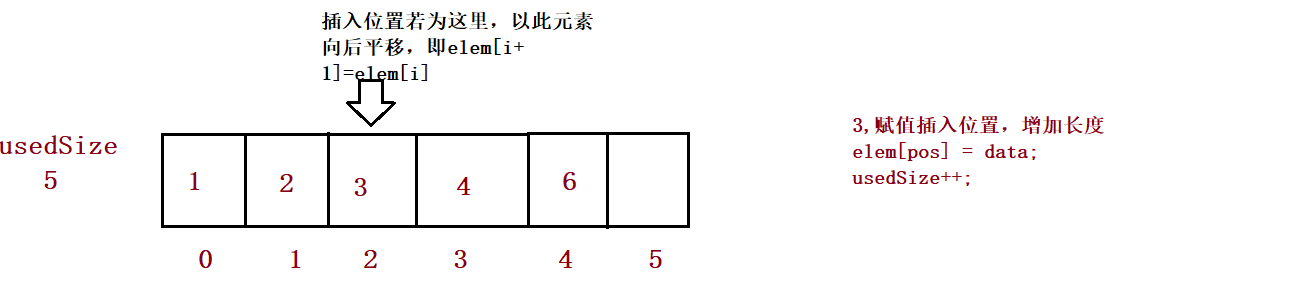
}⑥ Add element in pos position
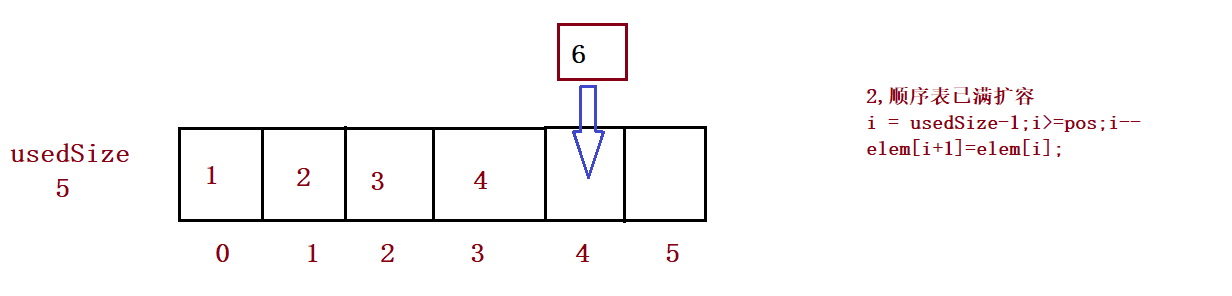
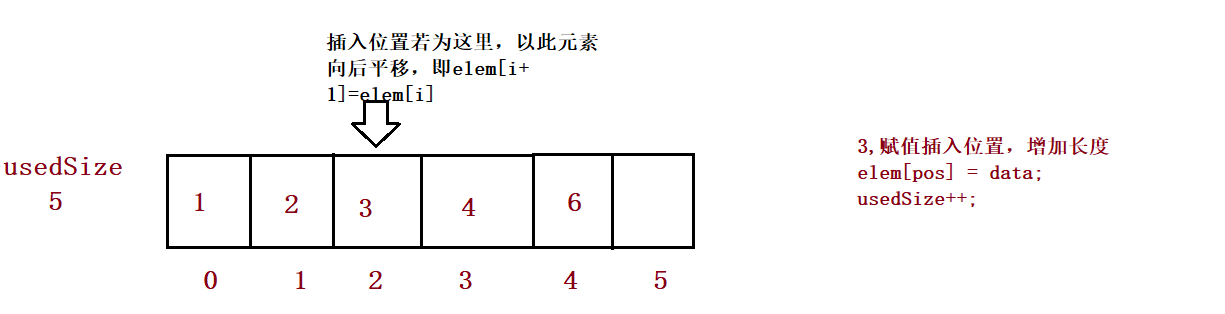
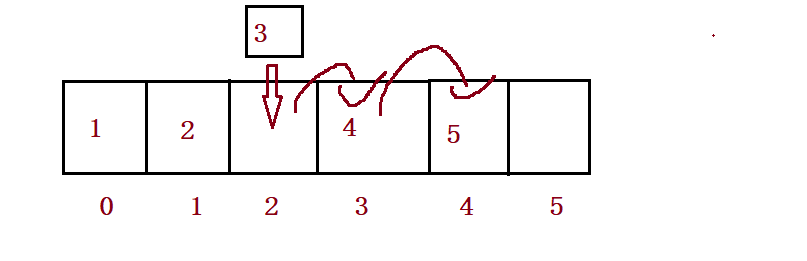
public boolean isFull() {
return this.usedSize == this.elem.length;
} // Add new element in pos position
public void add(int pos, int data) {
if(pos < 0 || pos > usedSize) {
System.out.println("pos Illegal location!");
return;
}
if(isFull()) {
this.elem = Arrays.copyOf(this.elem,2*this.elem.length);
}
//3,
for (int i = this.usedSize-1; i >= pos ; i--) {
this.elem[i+1] = this.elem[i];
}
this.elem[pos] = data;
this.usedSize++;
}public static void main(String[] args) {
MyArrayList myArrayList = new MyArrayList();
myArrayList.add(0,1);
myArrayList.add(1,2);
myArrayList.add(2,3);
myArrayList.add(3,4);
myArrayList.display();
}
⑦ Judge whether to find the corresponding position of an element. If not, return - 1
// Determines whether an element is included
public boolean contains(int toFind) {
for (int i = 0; i < this.usedSize; i++) {
if(this.elem[i] == toFind) {
return true;
}
}
return false;
} public int search(int toFind) {
for (int i = 0; i < this.usedSize; i++) {
if(this.elem[i] == toFind) {
return i;
}
}
return -1;
}⑧ Get the element of pos position and set / update the element of pos position to value
public int getPos(int pos) {
if(pos < 0 || pos >= this.usedSize) {
System.out.println("pos Illegal location");
return -1;//So let's explain here that exceptions can be thrown in the later stage of business processing
}
if(isEmpty()) {
System.out.println("Sequence table is empty!");
return -1;
}
return this.elem[pos];
}public boolean isEmpty() {
return this.usedSize==0;
} public void setPos(int pos, int value) {
if(pos < 0 || pos >= this.usedSize) {
System.out.println("pos Illegal location");
return;
}
if(isEmpty()) {
System.out.println("Sequence table is empty!");
return;
}
this.elem[pos] = value;
}⑨ Delete the keyword key that appears for the first time
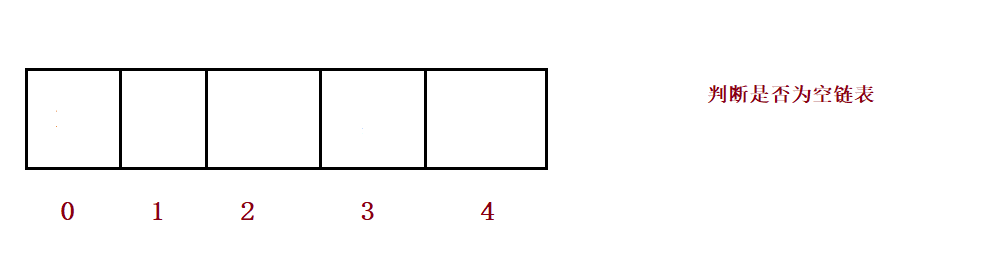
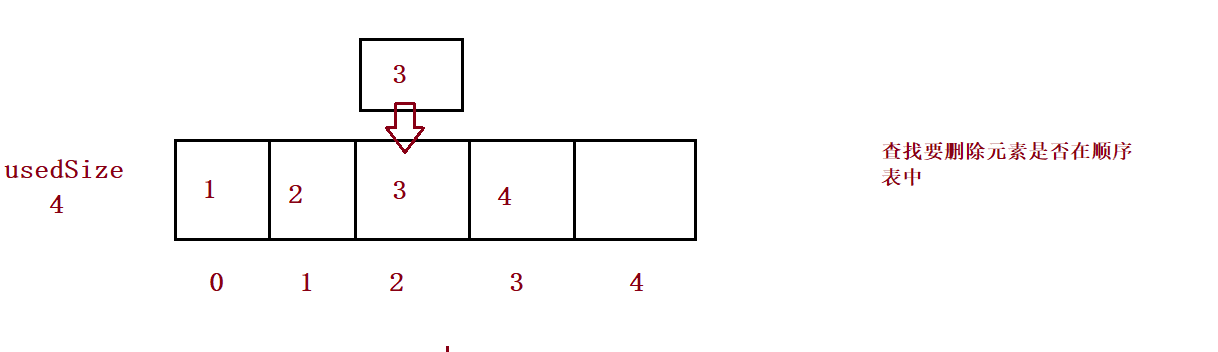
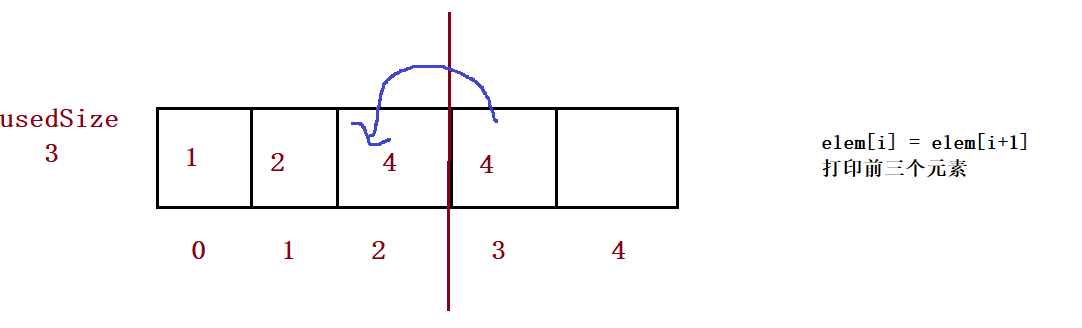
public void remove(int toRemove) {
if(isEmpty()) {
System.out.println("Sequence table is empty!");
return;
}
int index = search(toRemove);
if(index == -1) {
System.out.println("There are no numbers you want to delete!");
return;
}
for (int i = index; i < this.usedSize-1; i++) {
this.elem[i] = this.elem[i+1];
}
this.usedSize--;
//this.elem[usedSize] = null; If there is a reference data type in the array.
}public static void main(String[] args) {
MyArrayList myArrayList = new MyArrayList();
myArrayList.add(0,1);
myArrayList.add(1,2);
myArrayList.add(2,3);
myArrayList.add(3,4);
myArrayList.remove(3);
myArrayList.display();
}
3. Linked list
① Concept
Linked list is a discontinuous storage structure in physical storage structure. The logical order of data elements is realized through the reference link order in the linked list.
Linked list classification
② Implementation of linked list
// 1. Implementation of headless one-way acyclic linked list
public class SingleLinkedList {
//Head insertion
}
public void addFirst(int data){
//Tail interpolation
}
public void addLast(int data){
//Insert at any position, and the first data node is subscript 0
}
public boolean addIndex(int index,int data){
//Find out whether the keyword is included and whether the key is in the single linked list
}
public boolean contains(int key){
//Delete the node whose keyword is key for the first time
}
public void remove(int key){
//Delete all nodes with the value of key
}
public void removeAllKey(int key){
//Get the length of the single linked list
}
public int size(){
}
public void display(){
}
public void clear(){
}
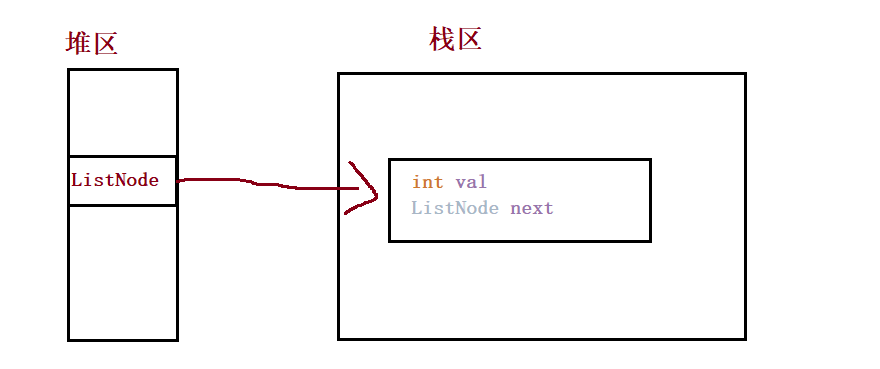
}③ Create node
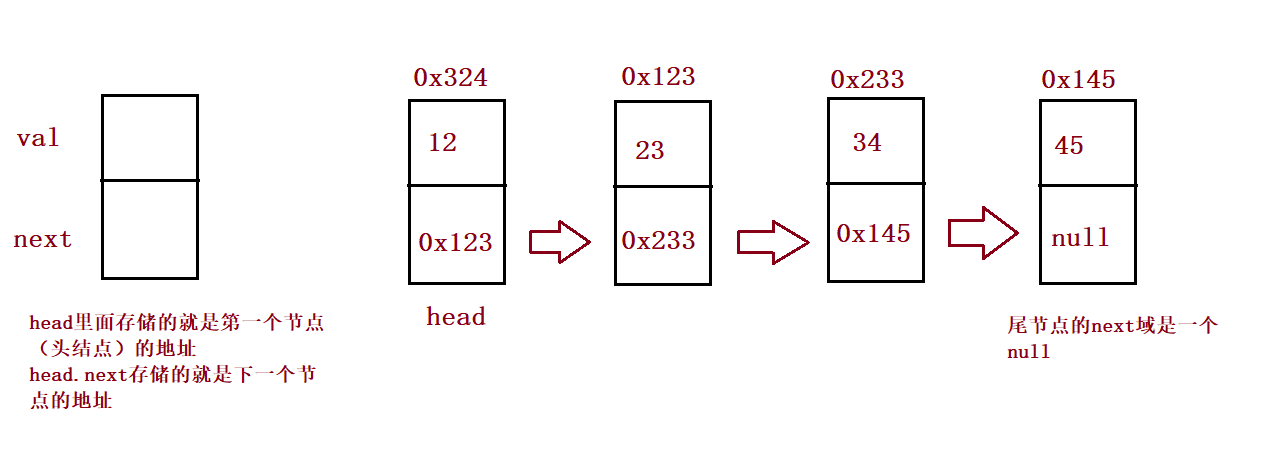
public ListNode head;//Header reference of linked list
lass ListNode {
public int val;
public ListNode next;//null
public ListNode(int val) {
this.val = val;
}
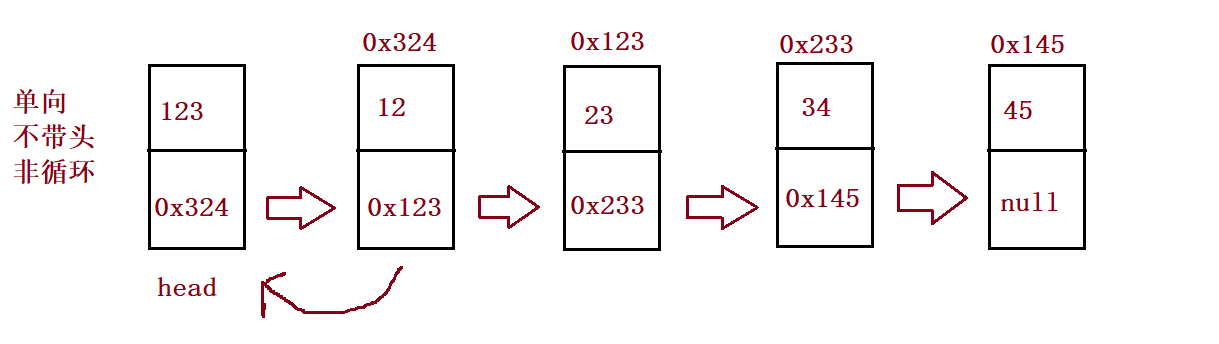
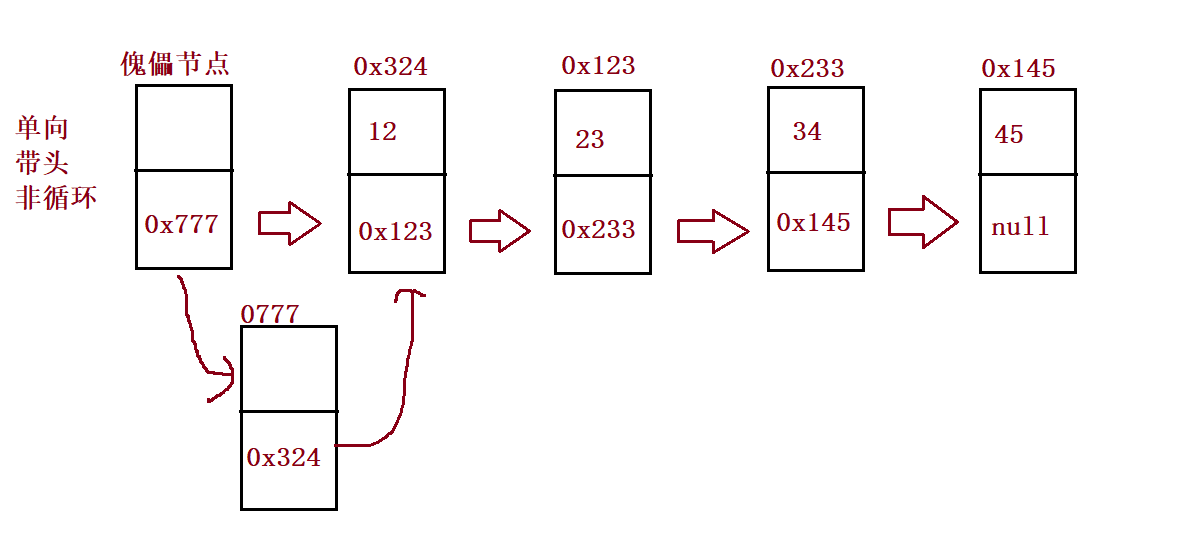
④ Create linked list and print linked list
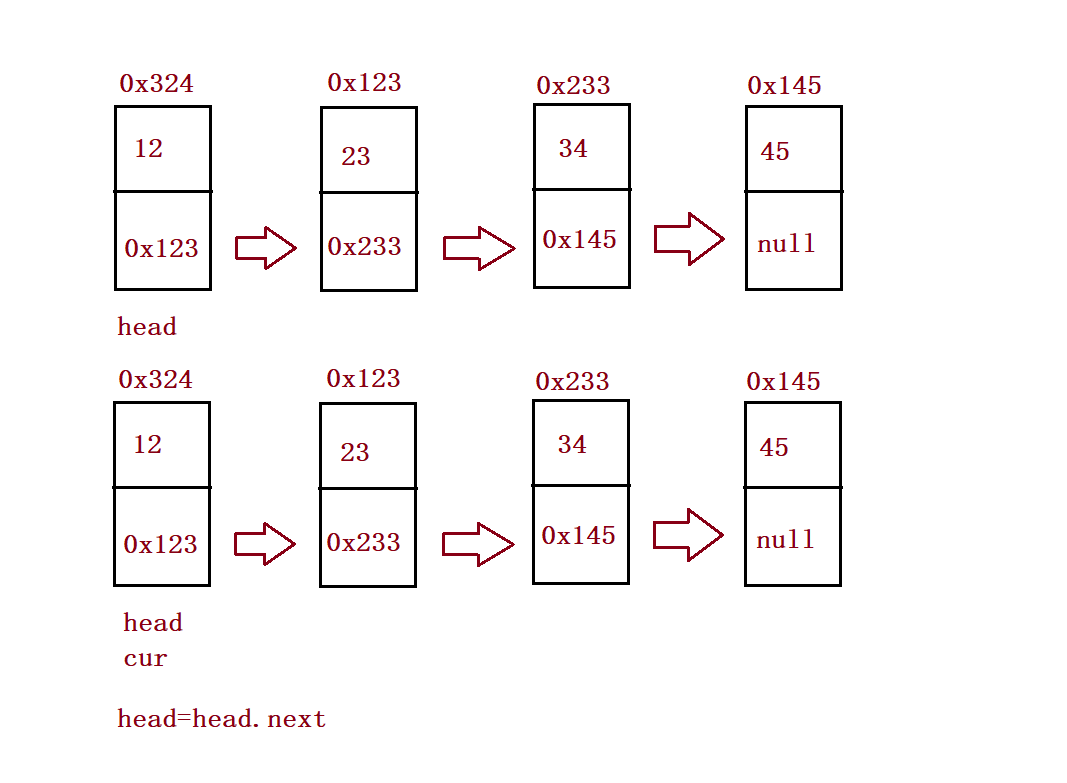
public void createList() {
ListNode listNode1 = new ListNode(12);
ListNode listNode2 = new ListNode(23);
ListNode listNode3 = new ListNode(34);
ListNode listNode4 = new ListNode(45);
ListNode listNode5 = new ListNode(56);
listNode1.next = listNode2;
listNode2.next = listNode3;
listNode3.next = listNode4;
listNode4.next = listNode5;
//listNode5.next = null;
this.head = listNode1;
}public void display() {
//this.head.next != null
ListNode cur = this.head;
while (cur != null) {
System.out.print(cur.val+" ");
cur = cur.next;
}
System.out.println();
} public static void main(String[] args) {
MyLinkedList myLinkedList = new MyLinkedList();
//myLinkedList.createList();
myLinkedList.addLast(12);
myLinkedList.addLast(23);
myLinkedList.addLast(34);
myLinkedList.addLast(45);
myLinkedList.addLast(56);
myLinkedList.display();
}
⑤ Find out whether the keyword key is included, whether the key is in the single linked list, and get the length of the single linked list
public boolean contains(int key){
ListNode cur = this.head;
while (cur != null) {
if(cur.val == key) {
return true;
}
cur = cur.next;
}
return false;
} public static void main(String[] args) {
MyLinkedList myLinkedList = new MyLinkedList();
//myLinkedList.createList();
myLinkedList.addLast(12);
myLinkedList.addLast(23);
myLinkedList.addLast(34);
myLinkedList.addLast(45);
myLinkedList.addLast(56);
myLinkedList.display();
boolean flg = myLinkedList.contains(56);
}public int size(){
int count = 0;
ListNode cur = this.head;
while (cur != null) {
count++;
cur = cur.next;
}
return count;
}public static void main(String[] args) {
MyLinkedList myLinkedList = new MyLinkedList();
//myLinkedList.createList();
myLinkedList.addLast(12);
myLinkedList.addLast(23);
myLinkedList.addLast(34);
myLinkedList.addLast(45);
myLinkedList.addLast(56);
System.out.println(myLinkedList.size());
}
⑥ head insertion method and tail insertion method
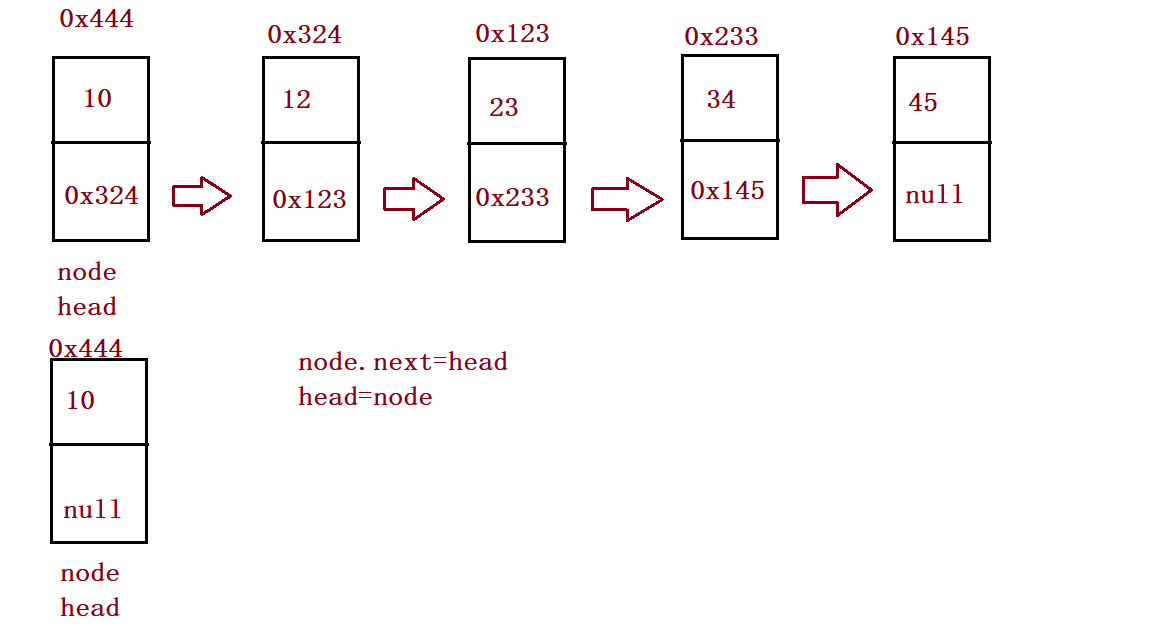
//Head insertion
public void addFirst(int data){
ListNode node = new ListNode(data);
node.next = this.head;
this.head = node;
/*if(this.head == null) {
this.head = node;
}else {
node.next = this.head;
this.head = node;
}*/
} public static void main(String[] args) {
MyLinkedList myLinkedList = new MyLinkedList();
//myLinkedList.createList();
myLinkedList.addLast(12);
myLinkedList.addLast(23);
myLinkedList.addLast(34);
myLinkedList.addLast(45);
myLinkedList.addLast(56);
myLinkedList.addFirst(10);
myLinkedList.display();
}
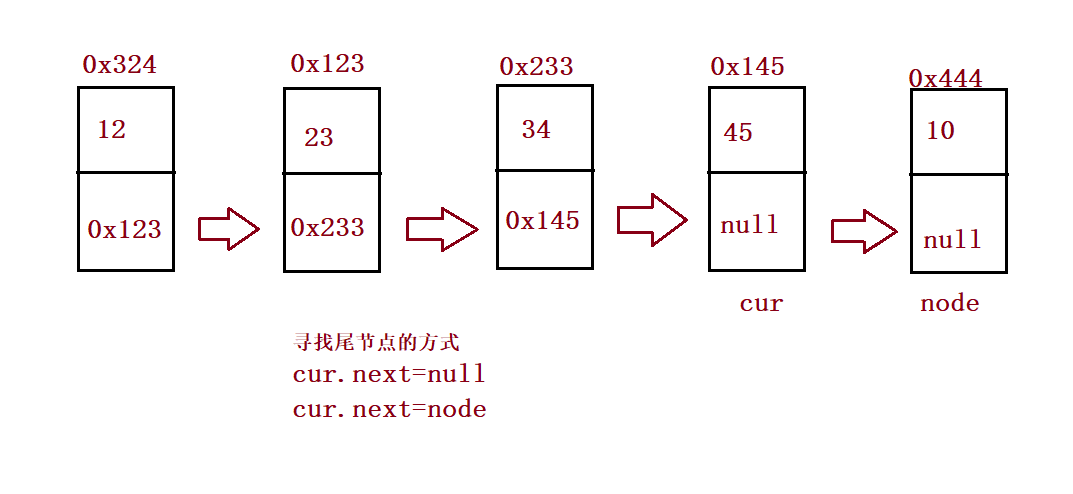
//Tail interpolation
public void addLast(int data){
ListNode node = new ListNode(data);
if(this.head == null) {
this.head = node;
}else {
ListNode cur = this.head;
while (cur.next != null) {
cur = cur.next;
}
//cur.next == null;
cur.next = node;
}
} public static void main(String[] args) {
MyLinkedList myLinkedList = new MyLinkedList();
//myLinkedList.createList();
myLinkedList.addLast(12);
myLinkedList.addLast(23);
myLinkedList.addLast(34);
myLinkedList.addLast(45);
myLinkedList.addLast(56);
myLinkedList.addLast(90);
myLinkedList.display();
}
⑦ Find the address of the node at index-1 and insert the element
public ListNode findIndex(int index) {
ListNode cur = this.head;
while (index-1 != 0) {
cur = cur.next;
index--;
}
return cur;
}
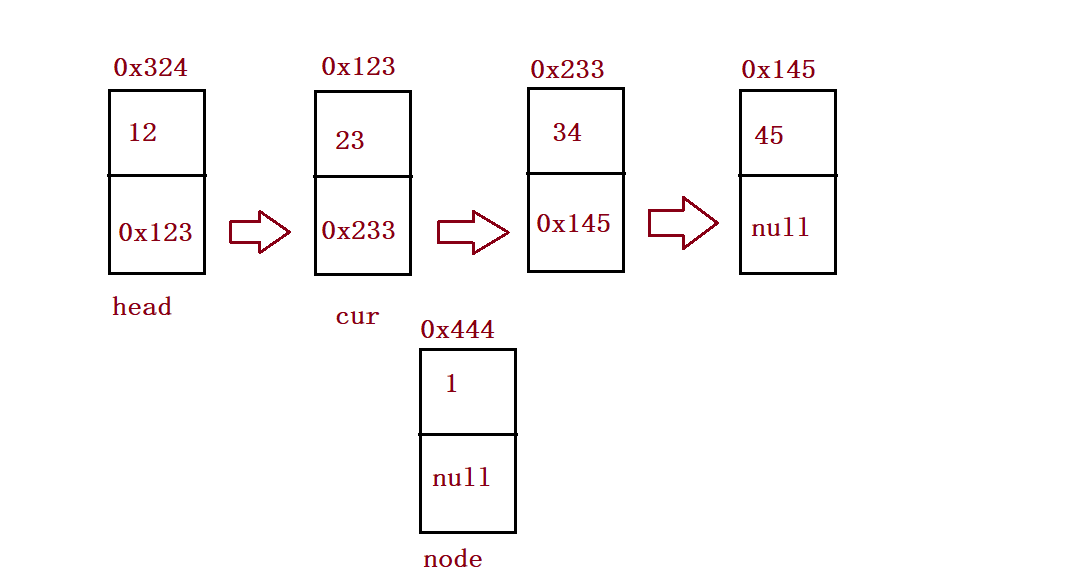
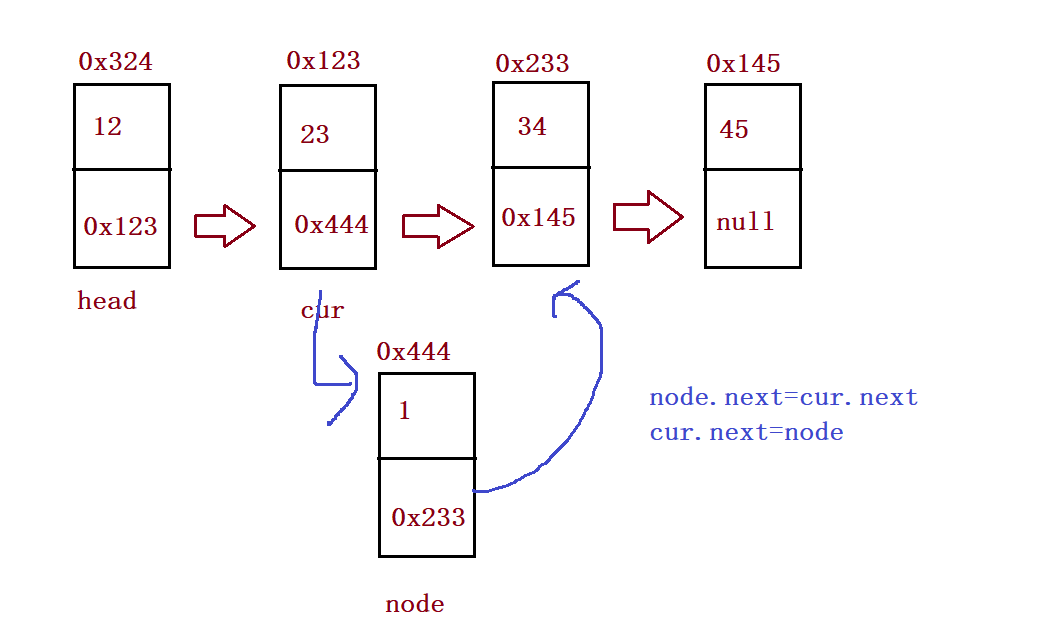
//Insert at any position, and the first data node is subscript 0
public void addIndex(int index,int data){
if(index < 0 || index > size()) {
System.out.println("index Illegal location!");
return;
}
if(index == 0) {
addFirst(data);
return;
}
if(index == size()) {
addLast(data);
return;
}
ListNode cur = findIndex(index);
ListNode node = new ListNode(data);
node.next = cur.next;
cur.next = node;
}public static void main(String[] args) {
MyLinkedList myLinkedList = new MyLinkedList();
//myLinkedList.createList();
myLinkedList.addLast(12);
myLinkedList.addLast(23);
myLinkedList.addLast(34);
myLinkedList.addLast(45);
myLinkedList.addLast(56);
myLinkedList.addLast(90);
myLinkedList.addIndex(2,20);
myLinkedList.display();
}
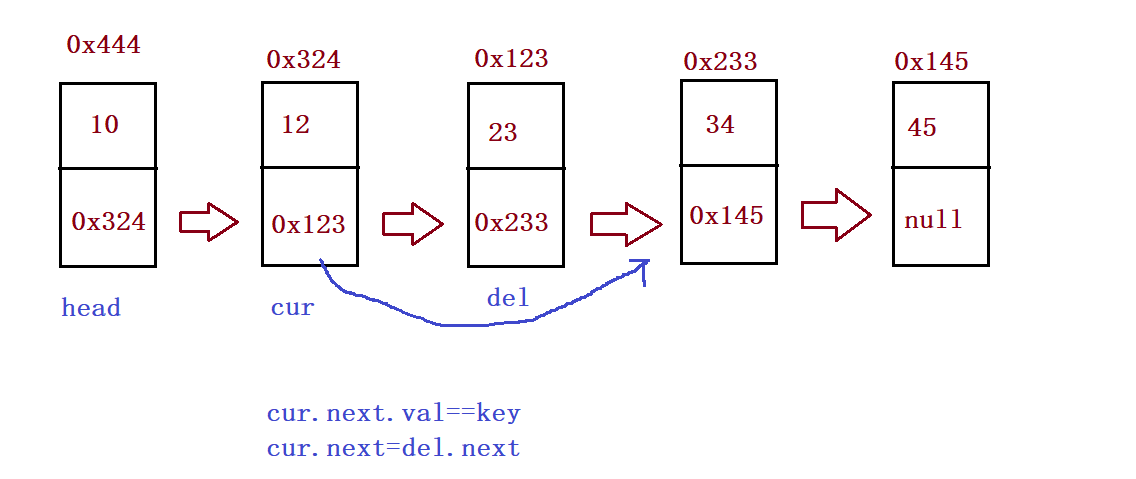
⑧ Find the precursor of the keyword to be deleted and delete the node whose keyword is key for the first time
public ListNode searchPerv(int key) {
ListNode cur = this.head;
while (cur.next != null) {
if(cur.next.val == key) {
return cur;
}
cur = cur.next;
}
return null;
}
//Delete the node whose keyword is key for the first time
public void remove(int key){
if(this.head == null) {
System.out.println("The single linked list is empty and cannot be deleted!");
return;
}
if(this.head.val == key) {
this.head = this.head.next;
return;
}
ListNode cur = searchPerv(key);
if(cur == null) {
System.out.println("There is no node you want to delete!");
return;
}
ListNode del = cur.next;
cur.next = del.next;
} public static void main(String[] args) {
MyLinkedList myLinkedList = new MyLinkedList();
//myLinkedList.createList();
myLinkedList.addLast(12);
myLinkedList.addLast(23);
myLinkedList.addLast(34);
myLinkedList.addLast(45);
myLinkedList.addLast(56);
myLinkedList.addLast(90);
myLinkedList.remove(23);
myLinkedList.display();
}
⑨ Delete all nodes with the value of key
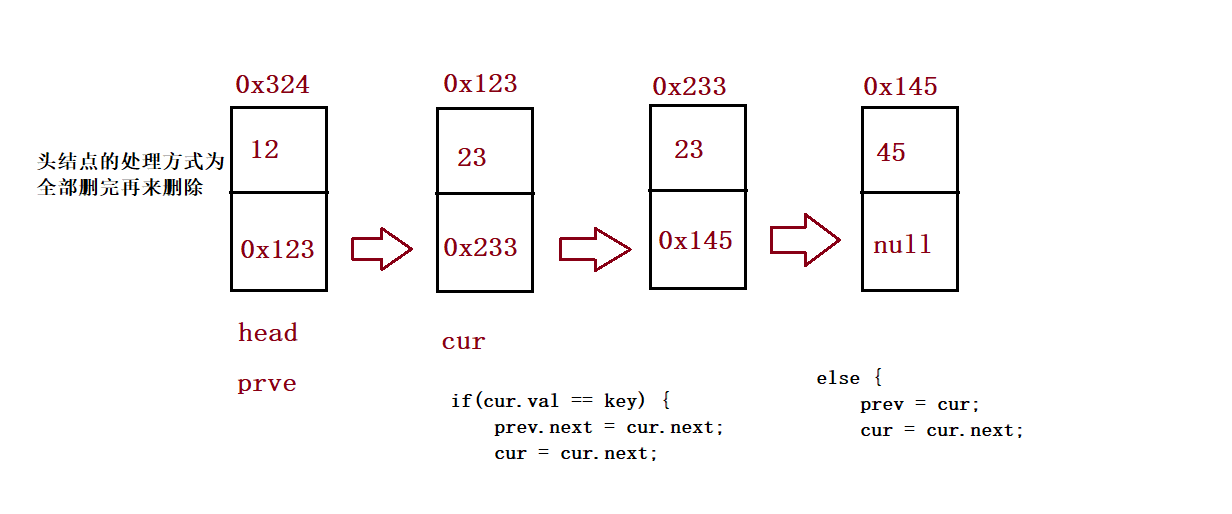
//Delete all nodes with the value of key
public ListNode removeAllKey(int key){
if(this.head == null) return null;
ListNode prev = this.head;
ListNode cur = this.head.next;
while (cur != null) {
if(cur.val == key) {
prev.next = cur.next;
cur = cur.next;
}else {
prev = cur;
cur = cur.next;
}
}
//Final processing head
if(this.head.val == key) {
this.head = this.head.next;
}
return this.head;
}public static void main(String[] args) {
MyLinkedList myLinkedList = new MyLinkedList();
//myLinkedList.createList();
myLinkedList.addLast(12);
myLinkedList.addLast(23);
myLinkedList.addLast(23);
myLinkedList.addLast(23);
myLinkedList.addLast(56);
myLinkedList.addLast(90);
myLinkedList.removeAllKey(23);
myLinkedList.display();
}
⑩ clear the linked list
public void clear(){
//this.head == null
while (this.head != null) {
ListNode curNext = head.next;
this.head.next = null;
this.head = curNext;
}
}4. Bidirectional linked list
① Implementation of linked list
public class DoubleLinkedList {
//Head insertion
public void addFirst(int data){
}
//Tail interpolation
public void addLast(int data){
}
//Insert at any position, and the first data node is subscript 0
public boolean addIndex(int index,int data){
}
//Find out whether the keyword is included and whether the key is in the single linked list
public boolean contains(int key){
}
//Delete the node whose keyword is key for the first time
public void remove(int key){
}
//Delete all nodes with the value of key
public void removeAllKey(int key){
}
//Get the length of the single linked list
public int size(){
}
public void display(){
}
public void clear(){
}
}② Construct nodes and linked lists
public static void main(String[] args) {
MyLinkedList myLinkedList = new MyLinkedList();
} public ListNode head;//Point to the head node of the bidirectional linked list
//public ListNode head = new ListNode(-1);// Point to the head node of the bidirectional linked list
public ListNode last;//It points to the tail node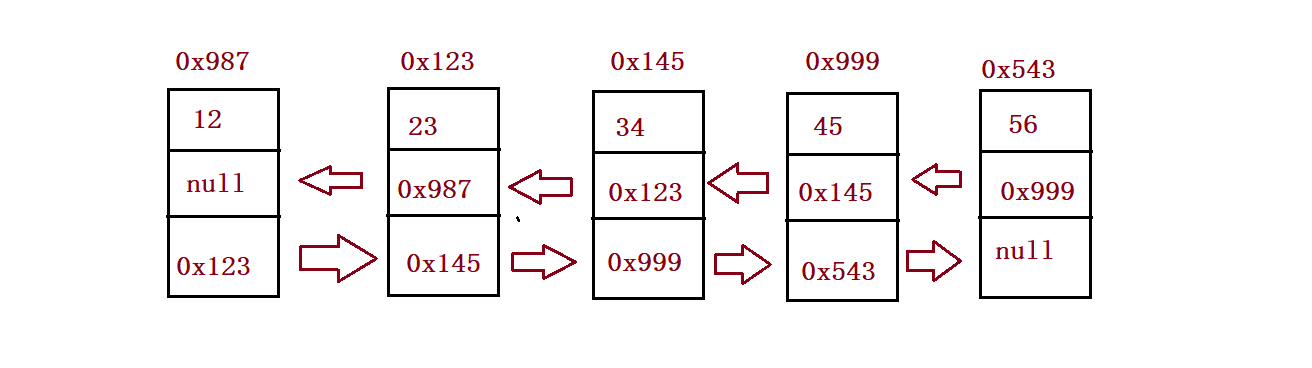
③ Print the linked list and calculate the length of the linked list
public void display() {
//The printing method is the same as that of single linked list
ListNode cur = this.head;
while (cur != null) {
System.out.print(cur.val+" ");
cur = cur.next;
}
System.out.println();
}/Get the length of the single linked list
public int size() {
int count = 0;
ListNode cur = this.head;
while (cur != null) {
count++;
cur = cur.next;
}
return count;
}④ Query key
public boolean contains(int key){
ListNode cur = this.head;
while (cur != null) {
if(cur.val == key) {
return true;
}
cur = cur.next;
}
return false;
}⑤ Head insertion
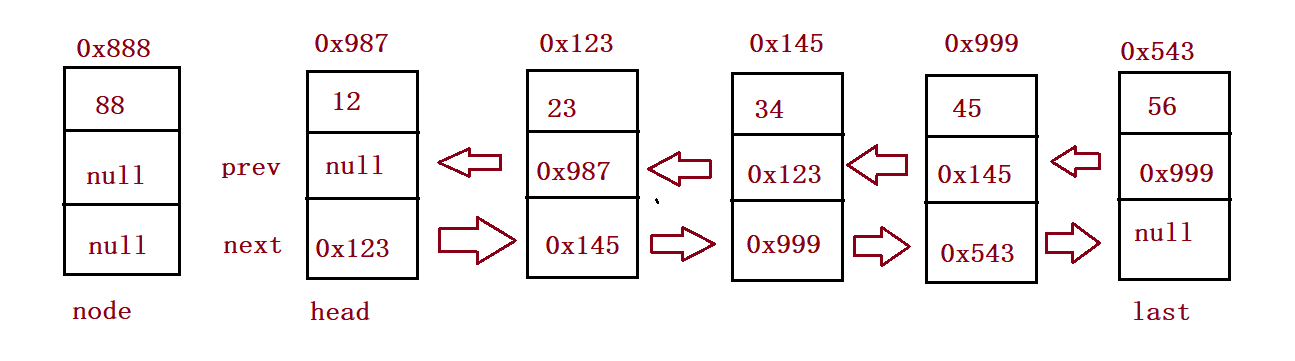
//Head insertion
public void addFirst(int data) {
ListNode node = new ListNode(data);
if(this.head == null) {
this.head = node;
this.last = node;
}else {
node.next = this.head;
this.head.prev = node;
this.head = node;
}
} public static void main(String[] args) {
MyLinkedList myLinkedList = new MyLinkedList();
myLinkedList.addFirst(12);
myLinkedList.addFirst(23);
myLinkedList.addFirst(34);
myLinkedList.addFirst(45);
myLinkedList.addFirst(56);
myLinkedList.display();
}
⑥ Tail interpolation
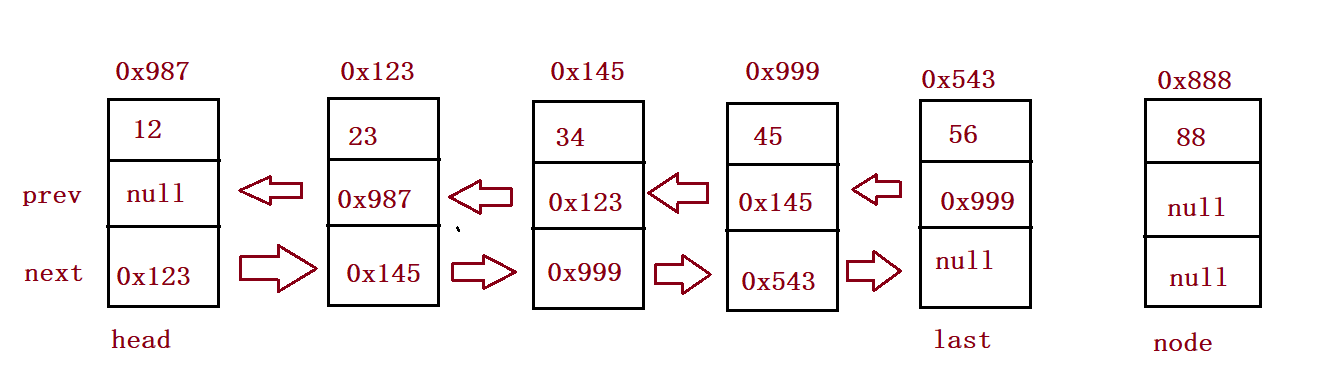
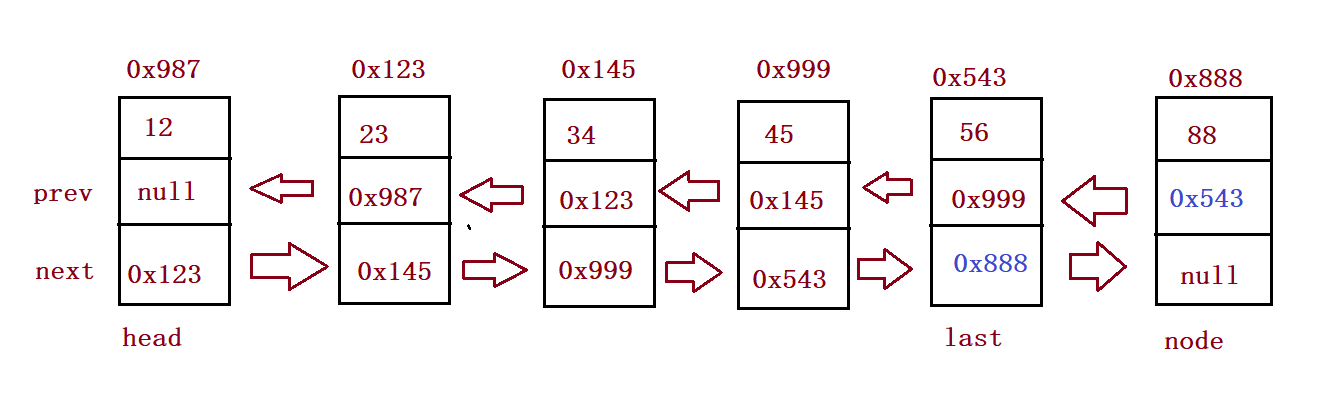
//Tail interpolation
public void addLast(int data){
ListNode node = new ListNode(data);
if(this.head == null) {
this.head = node;
this.last = node;
}else {
this.last.next = node;
node.prev = this.last;
this.last = node;
}
} public static void main(String[] args) {
MyLinkedList myLinkedList = new MyLinkedList();
myLinkedList.addLast(12);
myLinkedList.addLast(23);
myLinkedList.addLast(34);
myLinkedList.addLast(45);
myLinkedList.addLast(56);
myLinkedList.display();
}
⑦ Find insert node
public ListNode searchIndex (int index) {
ListNode cur = this.head;
while (index != 0) {
cur = cur.next;
index--;
}
return cur;
}⑧ Insert element
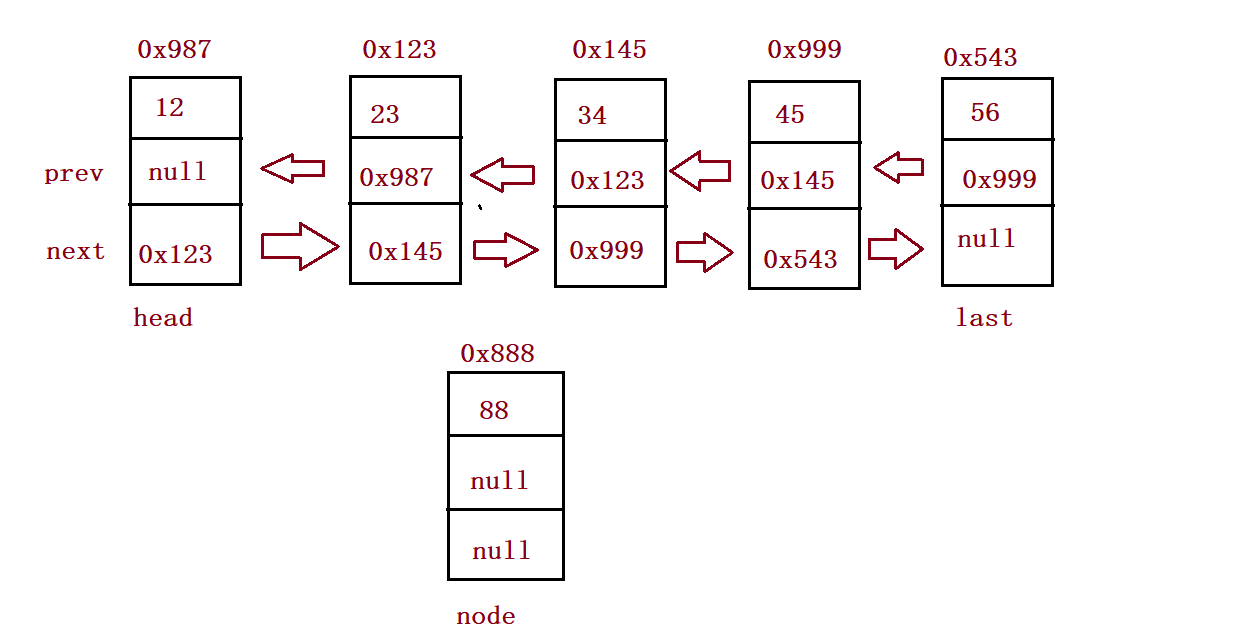
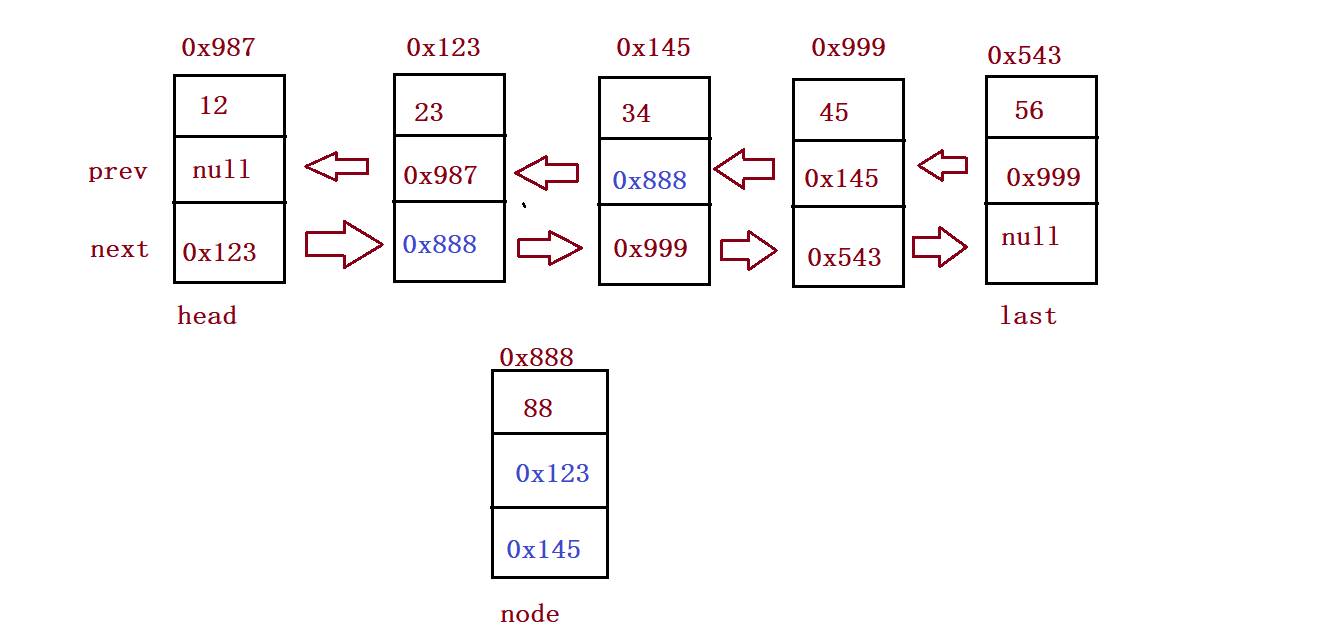
//Insert at any position, and the first data node is subscript 0
public void addIndex(int index,int data){
ListNode node = new ListNode(data);
if(index < 0 || index > size()) {
System.out.println("index Illegal location!");
return;
}
if(index == 0) {
addFirst(data);
return;
}
if(index == size()) {
addLast(data);
return;
}
ListNode cur = searchIndex(index);
node.next = cur.prev.next;
cur.prev.next = node;
node.prev = cur.prev;
cur.prev = node;
} public static void main(String[] args) {
MyLinkedList myLinkedList = new MyLinkedList();
myLinkedList.addLast(12);
myLinkedList.addLast(23);
myLinkedList.addLast(34);
myLinkedList.addLast(45);
myLinkedList.addLast(56);
myLinkedList.display();
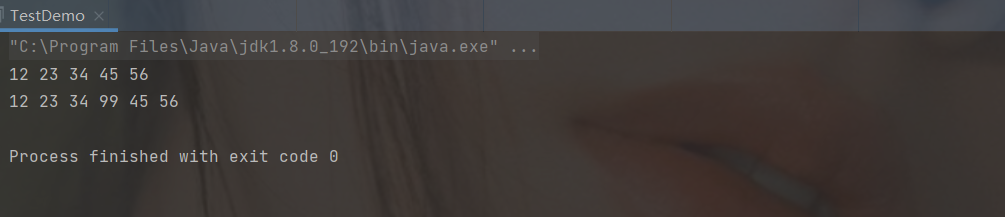
myLinkedList.addIndex(3,99);
myLinkedList.display();
}
⑨ Delete element
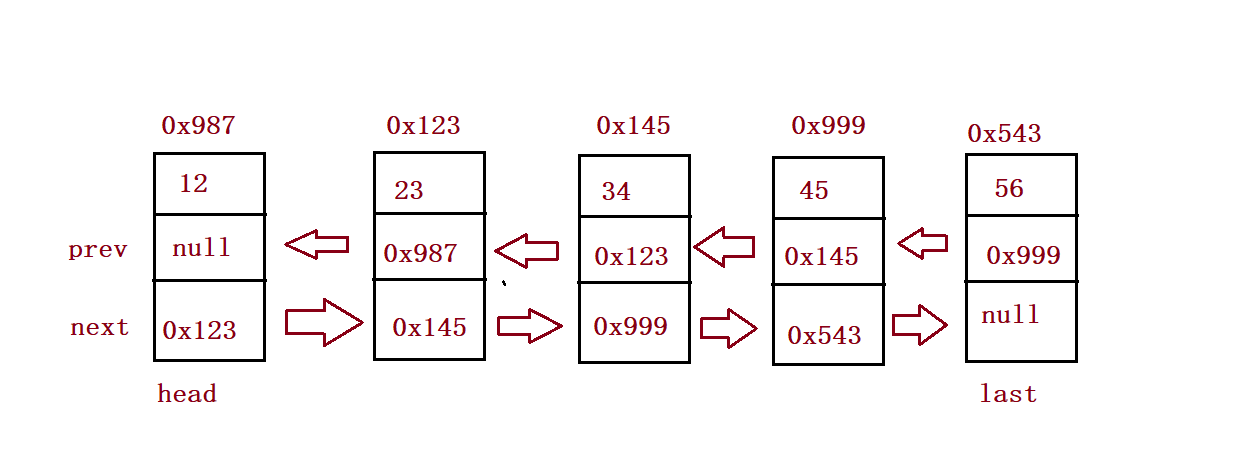
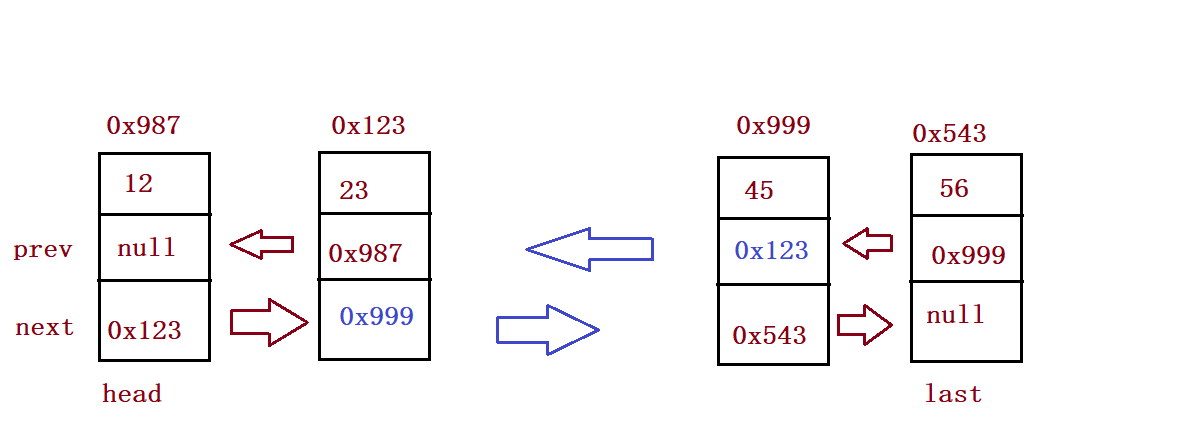
//Delete the node whose keyword is key for the first time
public void remove(int key){
ListNode cur = this.head;
while (cur != null) {
if(cur.val == key) {
if(cur == head) {
head = head.next;
if(head != null) {
head.prev = null;
}else {
last = null;
}
}else {
cur.prev.next = cur.next;
if(cur.next != null) {
//Middle position
cur.next.prev = cur.prev;
}else {
last = last.prev;
}
}
return;
}
cur = cur.next;
}
} public static void main(String[] args) {
MyLinkedList myLinkedList = new MyLinkedList();
myLinkedList.addLast(12);
myLinkedList.addLast(23);
myLinkedList.addLast(34);
myLinkedList.addLast(45);
myLinkedList.addLast(56);
myLinkedList.display();
myLinkedList.remove(23);
myLinkedList.display();
}
⑩ Empty linked list
public void clear() {
while (head != null) {
ListNode curNext = head.next;
head.next = null;
head.prev = null;
head = curNext;
}
last = null;
}5. Written test exercises
① Reverse a single linked list
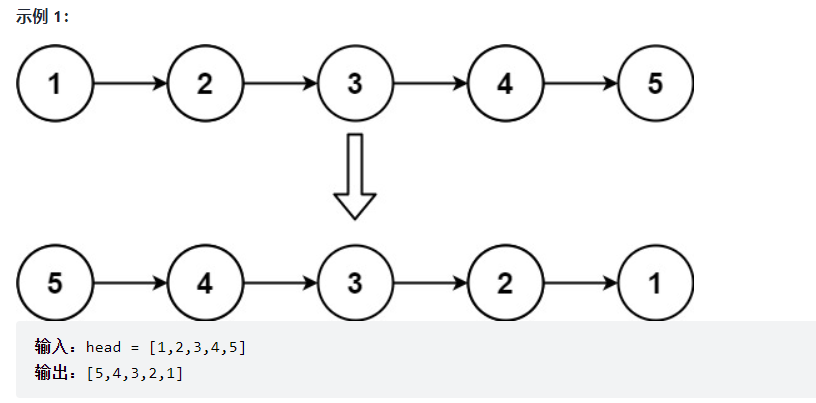
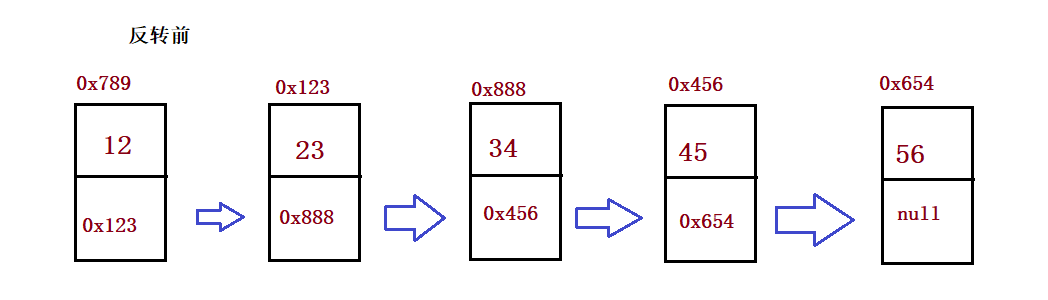
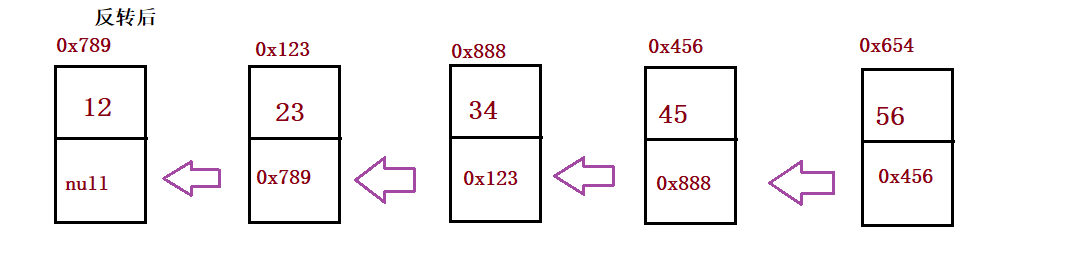
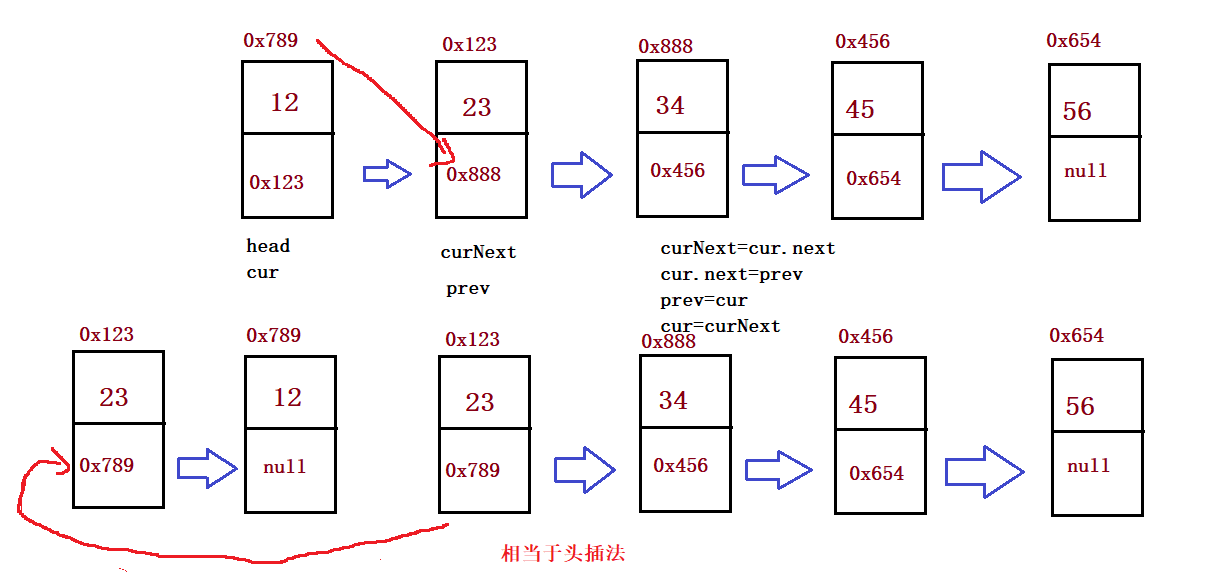
public ListNode reverseList() {
if(this.head == null) {
return null;
}
ListNode cur = this.head;
ListNode prev = null;
while (cur != null) {
ListNode curNext = cur.next;
cur.next = prev;
prev = cur;
cur = curNext;
}
return prev;
}② Given a non empty single linked list with head node, return the intermediate node of the linked list
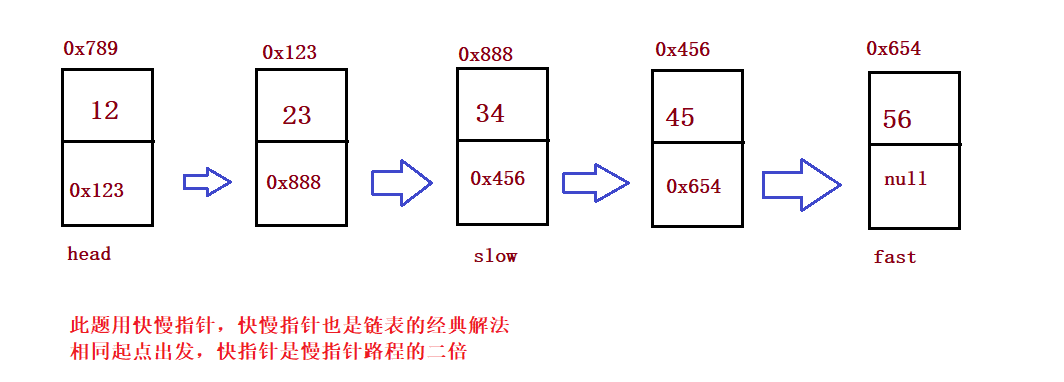
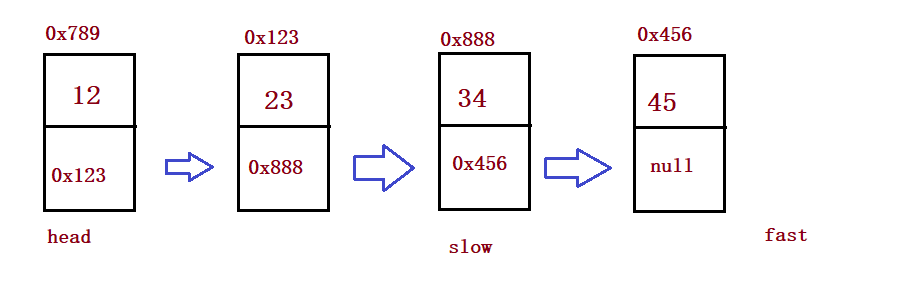
public ListNode middleNode() {
if(head == null) {
return null;
}
ListNode fast = head;
ListNode slow = head;
while(fast != null && fast.next != null){
fast = fast.next.next;
if(fast == null) {
return slow;
}
slow = slow.next;
}
return slow;
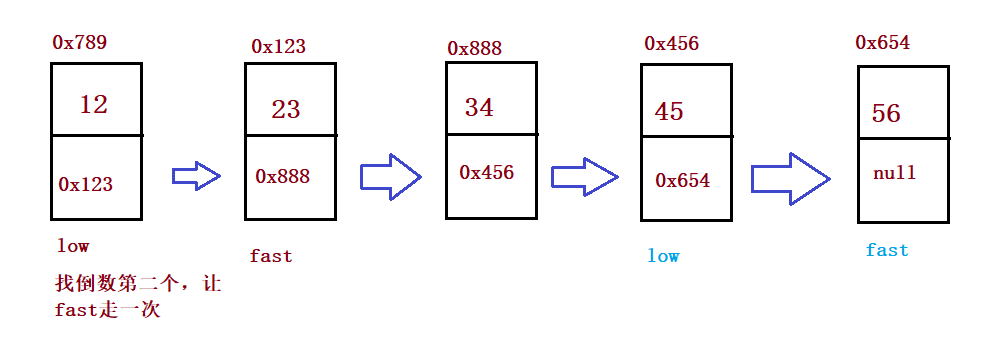
}③ Input a linked list and output the penultimate node in the linked list
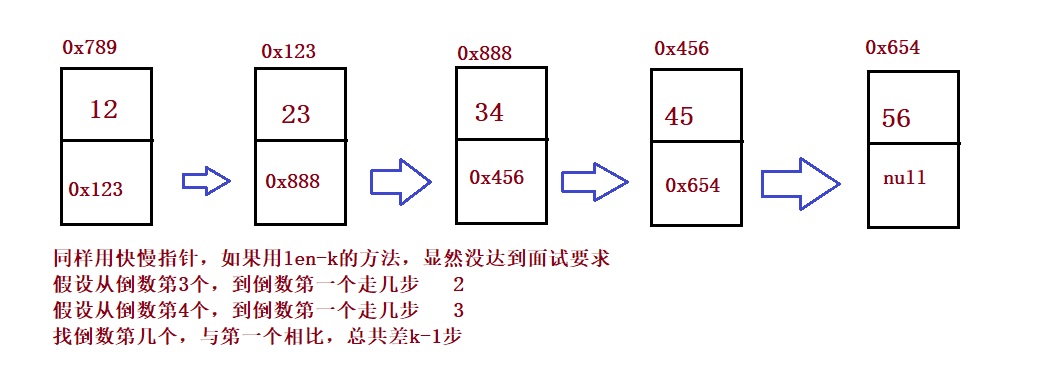
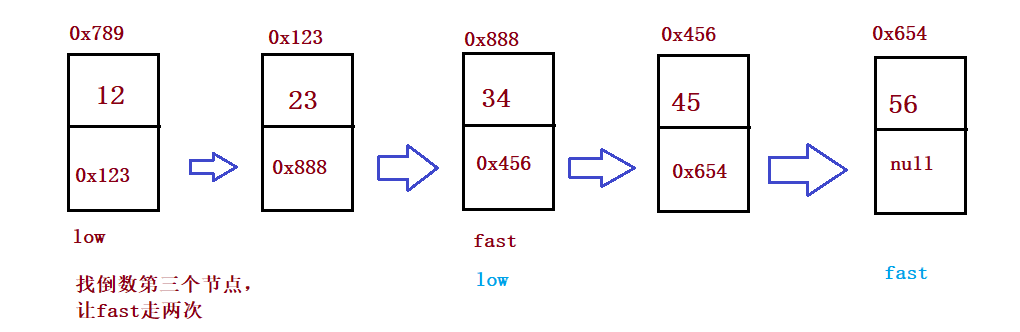
public ListNode findKthToTail(int k) {
if(k <= 0 || head == null) {
return null;
}
ListNode fast = head;
ListNode slow = head;
while (k-1 != 0) {
fast = fast.next;
if(fast == null) {
return null;
}
k--;
}
while (fast.next != null) {
fast = fast.next;
slow = slow.next;
}
return slow;
}④ Delete multiple duplicate values in the linked list
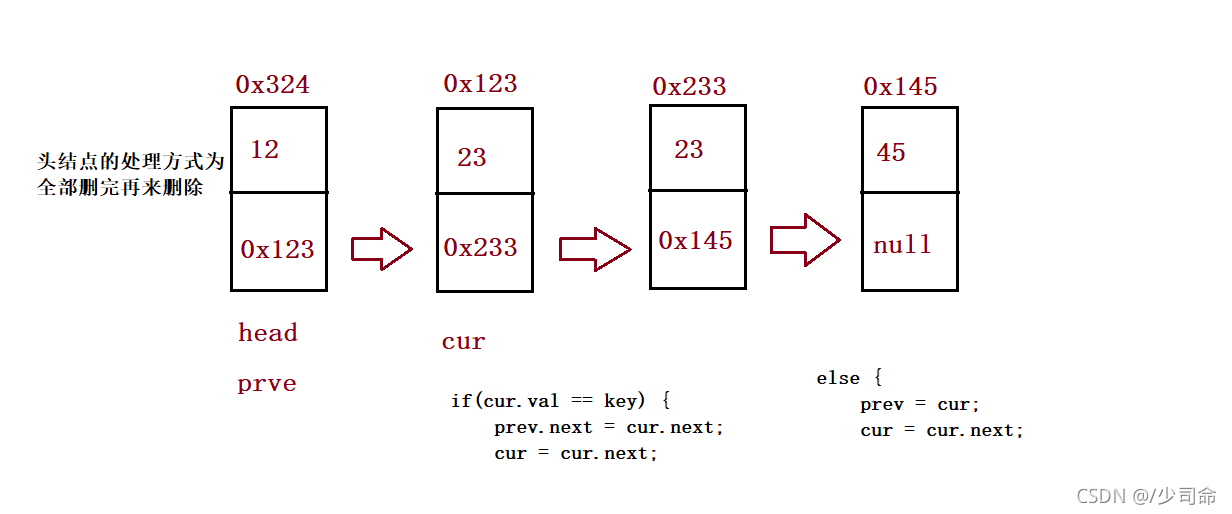
//Delete all nodes with the value of key
public ListNode removeAllKey(int key){
if(this.head == null) return null;
ListNode prev = this.head;
ListNode cur = this.head.next;
while (cur != null) {
if(cur.val == key) {
prev.next = cur.next;
cur = cur.next;
}else {
prev = cur;
cur = cur.next;
}
}
//Final processing head
if(this.head.val == key) {
this.head = this.head.next;
}
return this.head;
}⑤ Palindrome structure of linked list
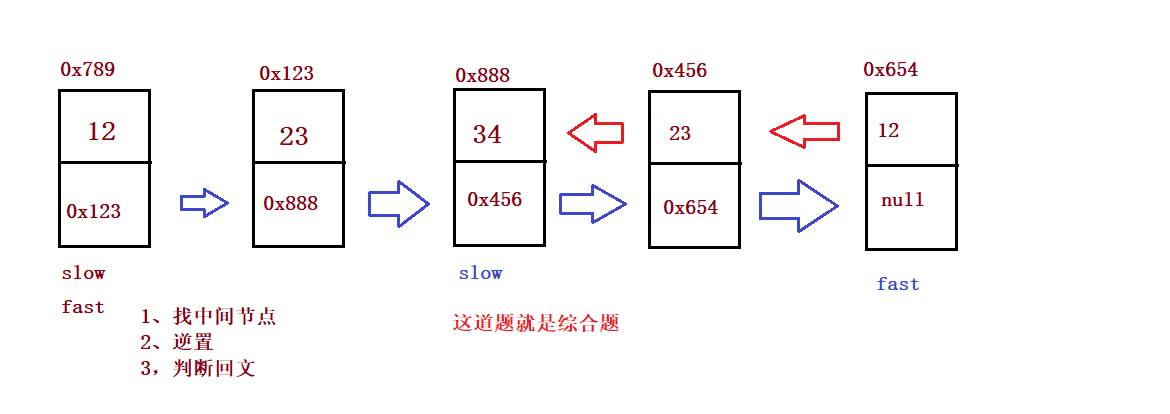
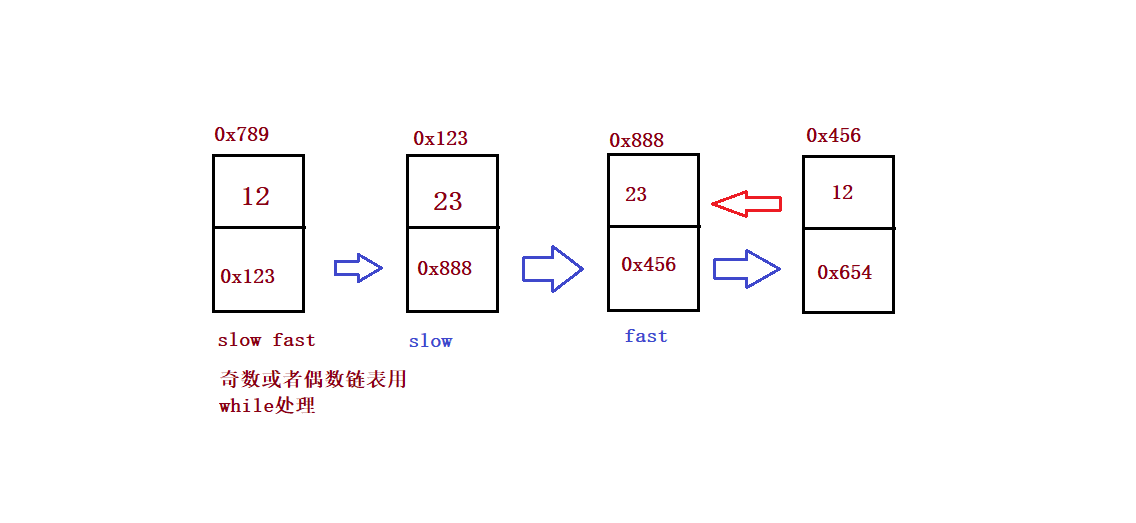
public boolean chkPalindrome(ListNode A) {
// write code here
if(head == null) return true;
ListNode fast = head;
ListNode slow = head;
while(fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
}
//slow goes to the middle position - "reverse"
ListNode cur = slow.next;
while(cur != null) {
ListNode curNext = cur.next;
cur.next = slow;
slow = cur;
cur = curNext;
}
//Reverse complete
while(head != slow) {
if(head.val != slow.val) {
return false;
}
if(head.next == slow) {
return true;
}
head = head.next;
slow = slow.next;
}
return true;
}⑥ Merge two linked lists
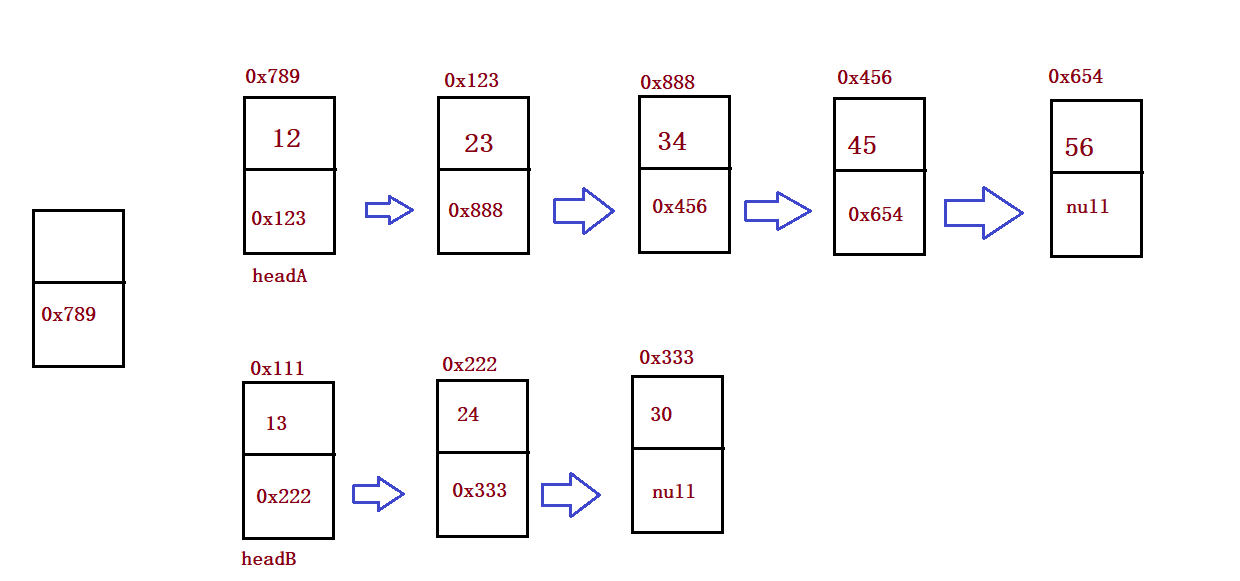
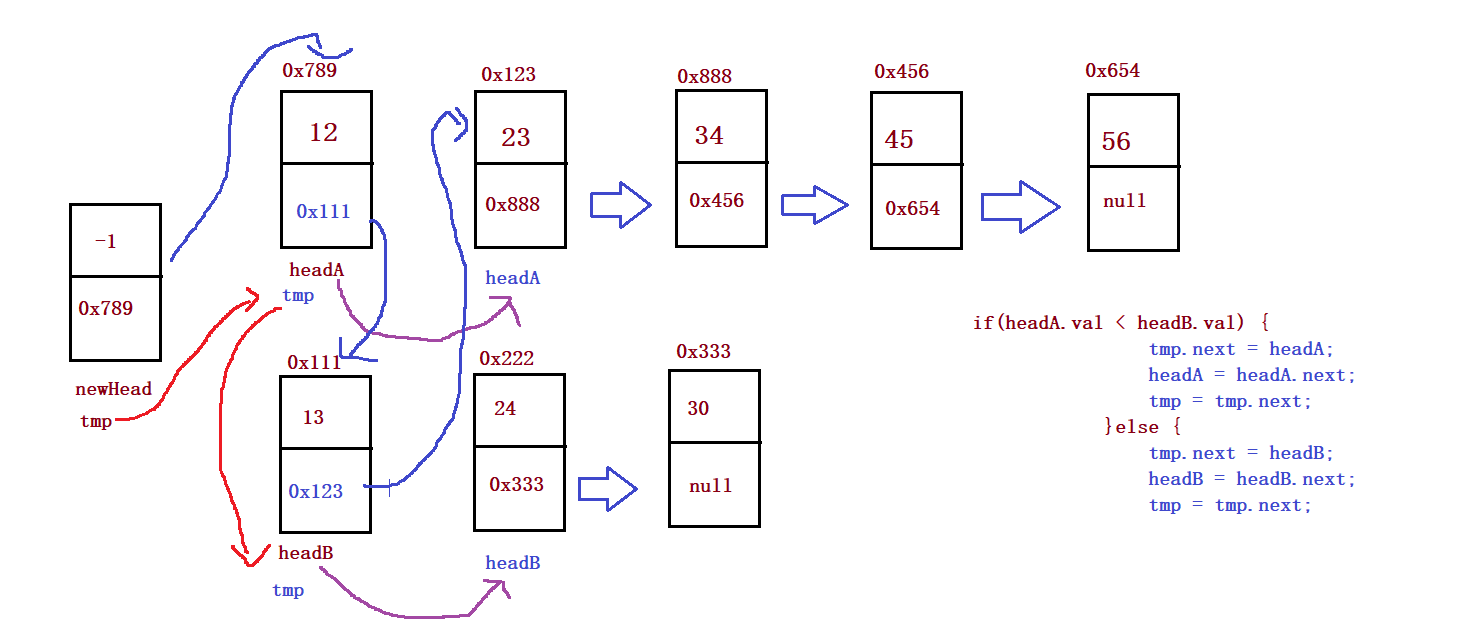
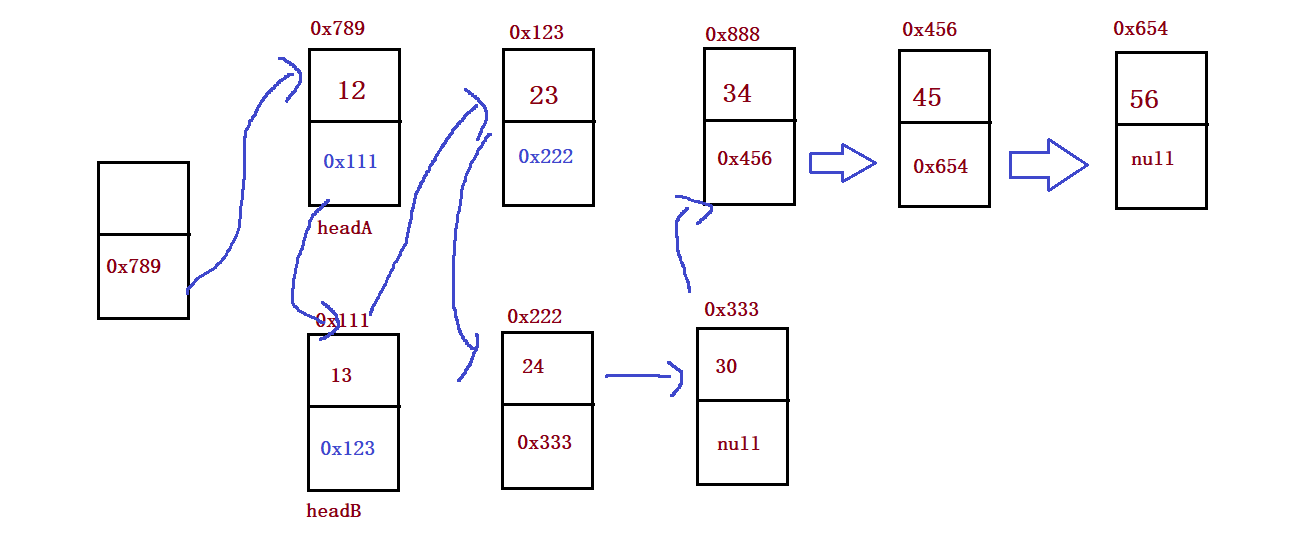
public static ListNode mergeTwoLists(ListNode headA, ListNode headB) {
ListNode newHead = new ListNode(-1);
ListNode tmp = newHead;
while (headA != null && headB != null) {
if(headA.val < headB.val) {
tmp.next = headA;
headA = headA.next;
tmp = tmp.next;
}else {
tmp.next = headB;
headB = headB.next;
tmp = tmp.next;
}
}
if(headA != null) {
tmp.next = headA;
}
if(headB != null) {
tmp.next = headB;
}
return newHead.next;
}⑦ Enter two linked lists and find their first common node
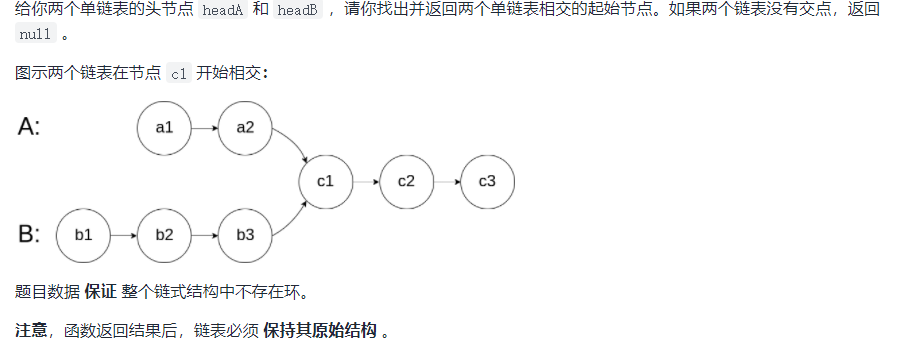
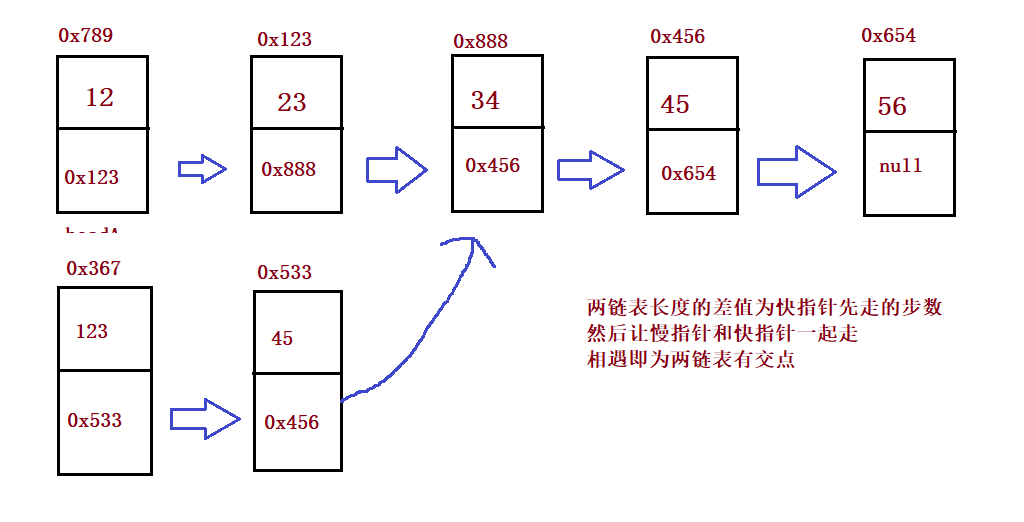
public static ListNode getIntersectionNode(ListNode headA, ListNode headB) {
if(headA == null || headB == null) {
return null;
}
ListNode pl = headA;
ListNode ps = headB;
int lenA = 0;
int lenB = 0;
while (pl != null) {
lenA++;
pl = pl.next;
}
//pl==null
pl = headA;
while (ps != null) {
lenB++;
ps = ps.next;
}
//ps==null
ps = headB;
int len = lenA-lenB;//Difference step
if(len < 0) {
pl = headB;
ps = headA;
len = lenB-lenA;
}
//1. pl always points to the longest list and ps always points to the shortest list. 2. Find the difference len step
//pl step len
while (len != 0) {
pl = pl.next;
len--;
}
//Walk together until you meet
while (pl != ps) {
pl = pl.next;
ps = ps.next;
}
return pl;
}⑧ Determine whether a linked list has a ring
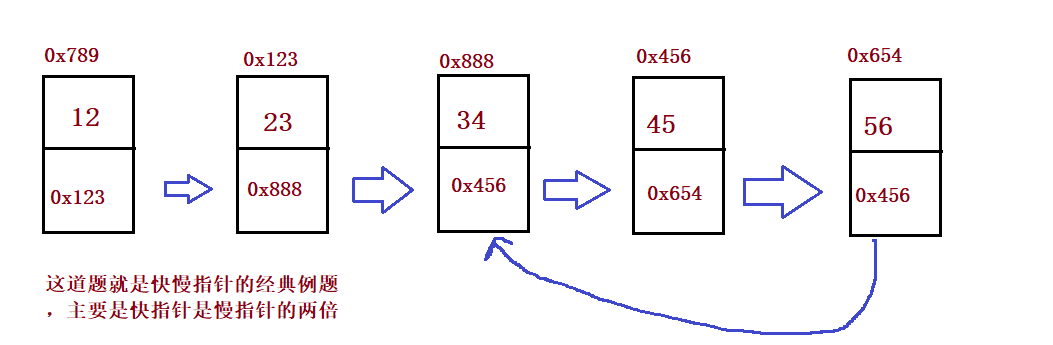
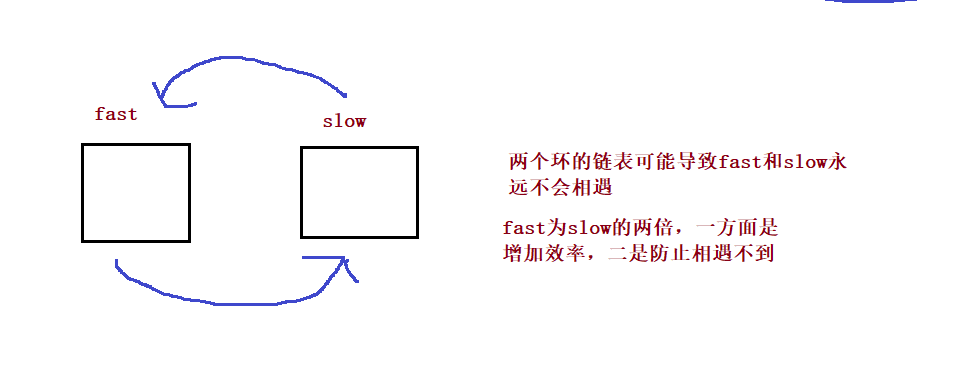
public boolean hasCycle() {
if(head == null) return false;
ListNode fast = head;
ListNode slow = head;
while(fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if(fast == slow) {
return true;
}
}
return false;
}⑨ Find the first node of a linked list
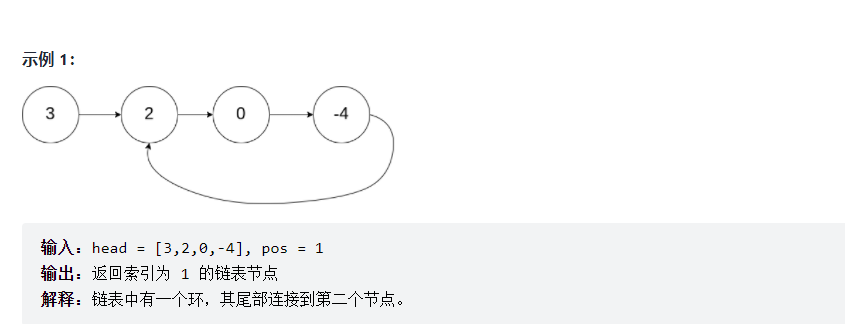
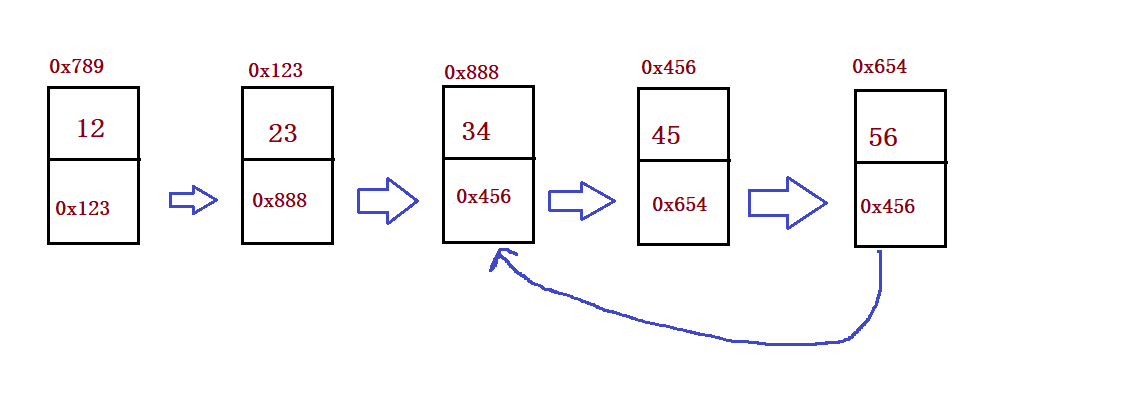
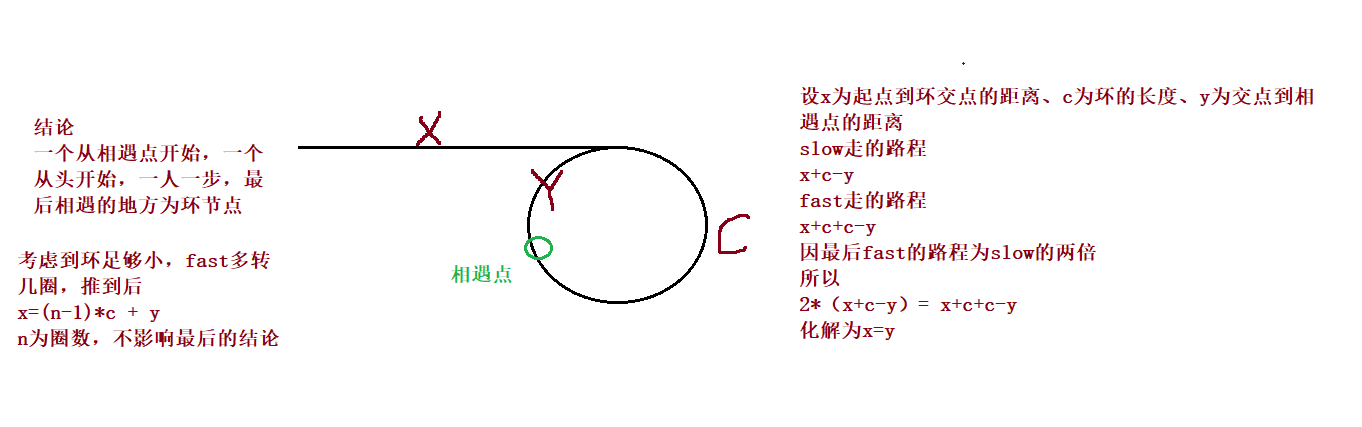
public ListNode detectCycle(ListNode head) {
if(head == null) return null;
ListNode fast = head;
ListNode slow = head;
while(fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if(fast == slow) {
break;
}
}
if(fast == null || fast.next == null) {
return null;
}
fast = head;
while (fast != slow) {
fast = fast.next;
slow = slow.next;
}
return fast;
}3, Stack and queue
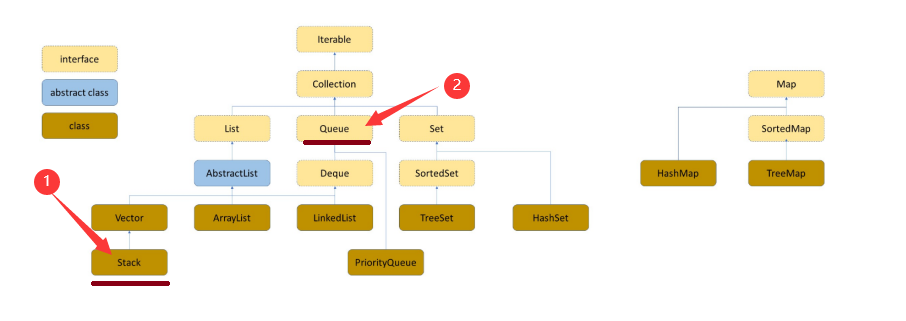
1. Stack
① Concept
In our software applications, stack, a last in first out data structure, is very common. For example, when you use the browser to surf the Internet, no matter what browser has a "back" button. After you click it, you can load the viewed web pages in reverse order.
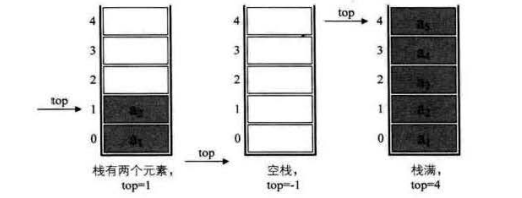
Many similar software, such as word, Photoshop and other document or image editing software, also use stack to realize the operation. Of course, the specific implementation of different software will be very different, but the principle is actually the same
A stack is a linear table that is restricted to insertion and deletion only at the end of the table
Stack: a special linear table that allows insertion and deletion of elements only at a fixed end. One end for data insertion and deletion is called the top of the stack, and the other end is called the bottom of the stack. The data elements in the stack follow the principle of Last In First Out LIFO (Last In First Out).
② Stack operation
Stack pressing: the stack insertion operation is called stack entering / stack pressing / stack entering, and the input data is at the top of the stack.
Stack out: stack deletion is called stack out. The output data is at the top of the stack.
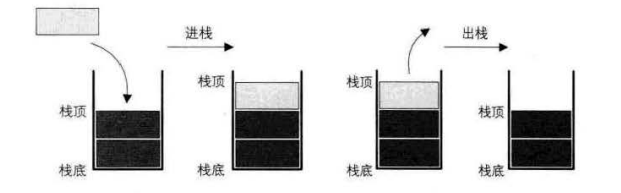
③ Implementation of stack
Push
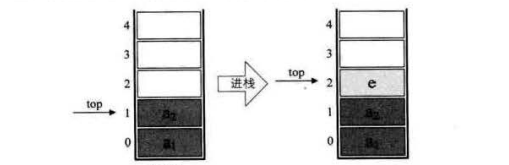
public static void main(String[] args) {
Stack<Integer> stack = new Stack<>();
stack.push(1);
stack.push(2);
stack.push(3);
stack.push(4);
int ret = stack.push(4);
System.out.println(ret);
}
Out of stack
public static void main(String[] args) {
Stack<Integer> stack = new Stack<>();
stack.push(1);
stack.push(2);
stack.push(3);
int ret1 = stack.pop();
int ret2 = stack.pop();
System.out.println(ret1);
System.out.println(ret2);
}
Get stack top element
public static void main(String[] args) {
Stack<Integer> stack = new Stack<>();
stack.push(1);
stack.push(2);
stack.push(3);
int ret1 = stack.pop();
int ret2 = stack.pop();
int ret3 = stack.peek();
System.out.println(ret1);
System.out.println(ret2);
System.out.println(ret3);
}
Determine whether the stack is empty
public static void main(String[] args) {
Stack<Integer> stack = new Stack<>();
stack.push(1);
stack.push(2);
stack.push(3);
int ret1 = stack.pop();
int ret2 = stack.pop();
int ret3 = stack.peek();
System.out.println(ret1);
System.out.println(ret2);
System.out.println(ret3);
stack.pop();
boolean flag = stack.empty();
System.out.println(flag);
}
④ Implement mystack
public class MyStack<T> {
private T[] elem;//array
private int top;//Currently, the subscript of the data element can be stored - "stack top pointer"
public MyStack() {
this.elem = (T[])new Object[10];
}
/**
* Stack operation
* @param item Stacked elements
*/
public void push(T item) {
//1. Determine whether the current stack is full
if(isFull()){
this.elem = Arrays.copyOf(this.elem,2*this.elem.length);
}
//2,elem[top] = item top++;
this.elem[this.top++] = item;
}
public boolean isFull(){
return this.elem.length == this.top;
}
/**
* Out of stack
* @return Out of stack elements
*/
public T pop() {
if(empty()) {
throw new UnsupportedOperationException("Stack is empty!");
}
T ret = this.elem[this.top-1];
this.top--;//Really changed the value of top
return ret;
}
/**
* Get the top element of the stack, but do not delete it
* @return
*/
public T peek() {
if(empty()) {
throw new UnsupportedOperationException("Stack is empty!");
}
//this.top--;// Really changed the value of top
return this.elem[this.top-1];
}
public boolean empty(){
return this.top == 0;
}
}public static void main(String[] args) {
MyStack<Integer> myStack = new MyStack<>();
myStack.push(1);
myStack.push(2);
myStack.push(3);
System.out.println(myStack.peek());
System.out.println(myStack.pop());
System.out.println(myStack.pop());
System.out.println(myStack.pop());
System.out.println(myStack.empty());
System.out.println("============================");
MyStack<String> myStack2 = new MyStack<>();
myStack2.push("hello");
myStack2.push("word");
myStack2.push("thank");
System.out.println(myStack2.peek());
System.out.println(myStack2.pop());
System.out.println(myStack2.pop());
System.out.println(myStack2.pop());
System.out.println(myStack2.empty());
}
2. Queue
① Concept
For customer service calls such as China Mobile, China Unicom and China Telecom, there are always a few customer service personnel compared with customers. When all customer service personnel are busy, customers will be asked to wait until a customer service personnel is free, so that the customer who waits first can connect the phone. Here, all customers who currently dial customer service calls are queued.
In the operating system and customer service system, a data structure is applied to realize the first in first out queuing function just mentioned, which is queue.
A queue is a linear table that only allows insertion at one end and deletion at the other
Queue: a special linear table that only allows inserting data at one end and deleting data at the other end. The queue has a first in first out FIFO(First In First Out) into the queue: the end at which inserting is called Tail/Rear out of the queue: the end at which deleting is called Head/Front
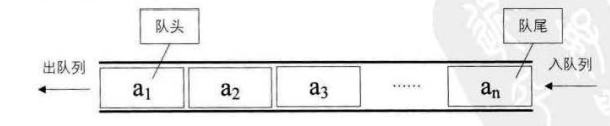
② Implementation of queue
Join the team
public static void main(String[] args) {
Deque<Integer> queue = new LinkedList<>();
queue.offer(1);
queue.offer(2);
queue.offer(3);
queue.offer(4);
}Out of the team
public static void main(String[] args) {
Deque<Integer> queue = new LinkedList<>();
queue.offer(1);
queue.offer(2);
queue.offer(3);
queue.offer(4);
System.out.println(queue.poll());
System.out.println(queue.poll());
}
Get team leader element
public static void main(String[] args) {
Deque<Integer> queue = new LinkedList<>();
queue.offer(1);
queue.offer(2);
queue.offer(3);
queue.offer(4);
System.out.println(queue.poll());
System.out.println(queue.poll());
System.out.println("-----------------");
System.out.println(queue.peek());
}
③ Implement myqueue
class Node {
private int val;
private Node next;
public int getVal() {
return val;
}
public void setVal(int val) {
this.val = val;
}
public Node getNext() {
return next;
}
public void setNext(Node next) {
this.next = next;
}
public Node(int val) {
this.val = val;
}
}
public class MyQueue {
private Node first;
private Node last;
//Join the team
public void offer(int val) {
//The tail interpolation method needs to judge whether it is the first insertion
Node node = new Node(val);
if(this.first == null) {
this.first = node;
this.last = node;
}else {
this.last.setNext(node);//last.next = node;
this.last = node;
}
}
//Out of the team
public int poll() {
//1 judge whether it is empty
if(isEmpty()) {
throw new UnsupportedOperationException("The queue is empty!");
}
//this.first = this.first.next;
int ret = this.first.getVal();
this.first = this.first.getNext();
return ret;
}
//Get the team header element but don't delete it
public int peek() {
//Do not move first
if(isEmpty()) {
throw new UnsupportedOperationException("The queue is empty!");
}
return this.first.getVal();
}
//Is the queue empty
public boolean isEmpty() {
return this.first == null;
}
} public static void main(String[] args) {
MyQueue myQueue = new MyQueue();
myQueue.offer(1);
myQueue.offer(2);
myQueue.offer(3);
System.out.println(myQueue.peek());
System.out.println(myQueue.poll());
System.out.println(myQueue.poll());
System.out.println(myQueue.poll());
System.out.println(myQueue.isEmpty());
}
4, Binary tree
1. Tree
① Concept
Tree is a non-linear data structure. It is a set with hierarchical relationship composed of n (n > = 0) finite nodes. It is called tree because it looks like an upside down tree, that is, it has roots facing up and leaves facing down. It has the following characteristics:
There is a special node, called the root node, which has no precursor node
Except for the root node, the other nodes are divided into m (M > 0) disjoint sets T1, T2 Tm, where each set Ti (1 < = I < = m) is a subtree similar to the tree. The root node of each subtree has only one precursor, and can have 0 or more successors
Trees are recursively defined.
② Basic concepts of tree
Node degree: the number of subtrees contained in a node is called the degree of the node
Tree degree: the degree of the largest node in a tree is called the degree of the tree
Leaf node or terminal node: a node with a degree of 0 is called a leaf node
Parent node or parent node: if a node has children, the node is called the parent node of its children
Child node or child node: the root node of the subtree contained in a node is called the child node of the node
Root node: a node in a tree without parent nodes
Node hierarchy: defined from the root, the root is the first layer, and the child nodes of the root are the second layer, and so on
Height or depth of the tree: the maximum level of nodes in the tree
2. Binary tree
① Concept
A binary tree is a finite set of nodes. The set is either empty or composed of a root node and two binary trees called left subtree and right subtree.
Characteristics of binary tree:
1. Each node has at most two subtrees, that is, the binary tree does not have nodes with a degree greater than 2.
2. The subtree of a binary tree can be divided into left and right, and the order of its subtrees cannot be reversed. Therefore, a binary tree is an ordered tree.
② Two special binary trees
1. Full binary tree: a binary tree. If the number of nodes in each layer reaches the maximum, the binary tree is a full binary tree. In other words, if the number of layers of a binary tree is K and the total number of nodes is, it is a full binary tree.
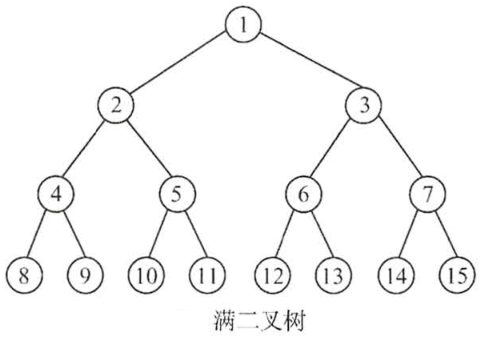
2. Complete binary tree: complete binary tree is a highly efficient data structure. Complete binary tree is derived from full binary tree. A binary tree with depth K and n nodes is called a complete binary tree if and only if each node corresponds to the nodes numbered from 1 to n in the full binary tree with depth K. It should be noted that full binary tree is a special complete binary tree.
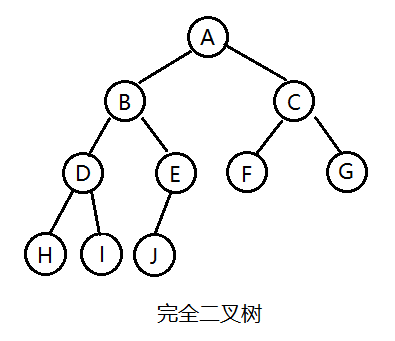
③ Properties of binary tree
1. If the specified number of layers of the root node is 1, there are at most 2 ^ (i-1) (I > 0) nodes on layer I of a non empty binary tree
2. If the depth of the binary tree with only the root node is specified as 1, the maximum number of nodes of the binary tree with depth K is 2 ^ k-1 (k > = 0)
3. For any binary tree, if the number of leaf nodes is n0 and the number of non leaf nodes with degree 2 is n2, then n0 = n2 + 1
4. The depth k of a complete binary tree with n nodes is rounded on log2(n+1)
3. Binary tree traversal
① Traversal of binary tree
Traversal means that each node in the tree is accessed once and only once along a search route. The operation of the access node depends on the specific application problem (for example, print the node content and add 1 to the node content). Traversal is one of the most important operations on a binary tree and the basis of other operations on a binary tree.
When traversing a binary tree, if there is no agreement, everyone traverses it in their own way, and the results are chaotic. If the agreement is made according to some rules, everyone must have the same traversal result for the same tree. If N represents the root node, L represents the left subtree of the root node, and R represents the right subtree of the root node, there are the following traversal methods according to the order of traversing the root node:
1. NLR: Preorder Traversal (also known as Preorder Traversal) - access the root node -- > the left subtree of the root -- > the right subtree of the root.
2. LNR: inorder traversal -- left subtree of root -- > root node -- > right subtree of root.
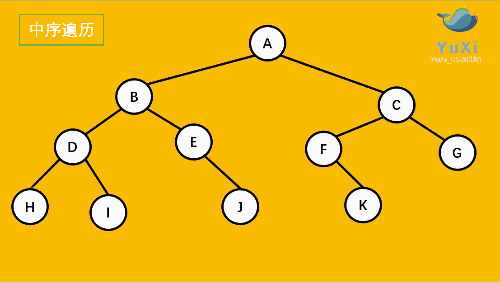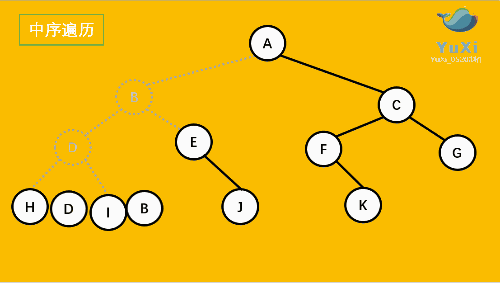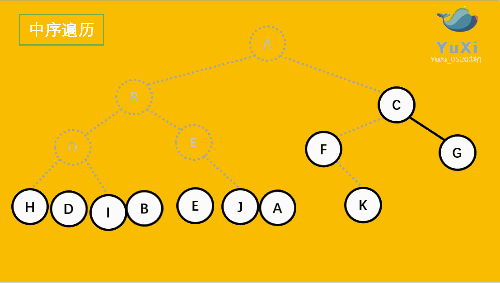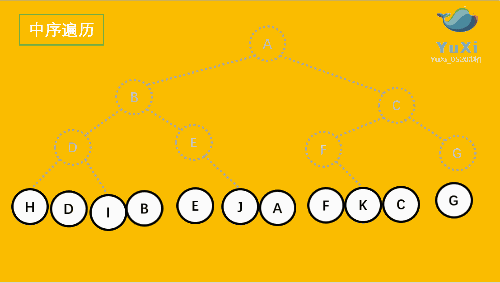
3. LRN: postorder traversal -- left subtree of root -- > right subtree of root -- > root node.
Since the accessed node must be the root of a subtree, N(Node), L(Left subtree) and R(Right subtree) can be interpreted as the root, the left subtree of the root and the right subtree of the root. NLR, LNR and LRN are also called first root traversal, middle root traversal and second root traversal respectively.
Note: among the three types of traversal, only the access root node prints. For each type of traversal, when accessing each node, there must be three different traversal methods until the traversal reaches null, return to the root node and continue to complete the traversal!!! For example, for preorder traversal, every time I visit a node, I have to perform the three steps of asking the root node -- > the left subtree of the root -- > the right subtree of the root. The middle order and post order traversal are the same.
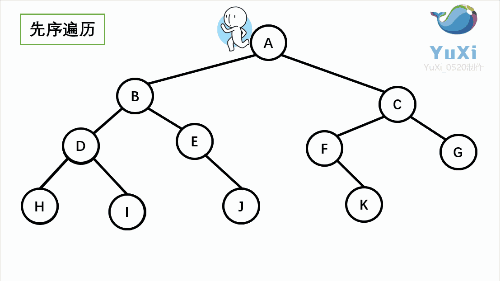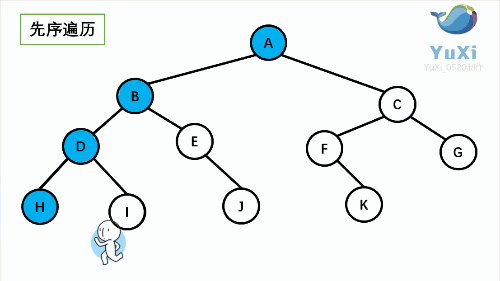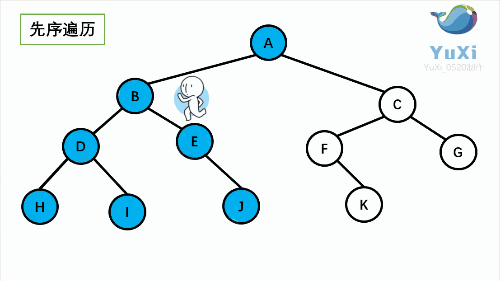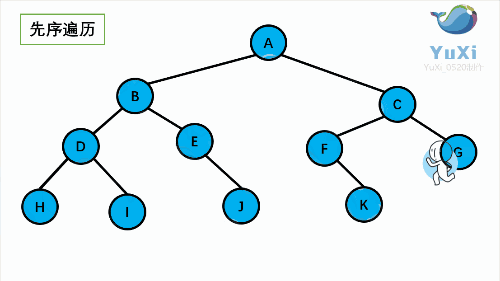
Taking the following binary tree as an example, the next step is to explain it in detail
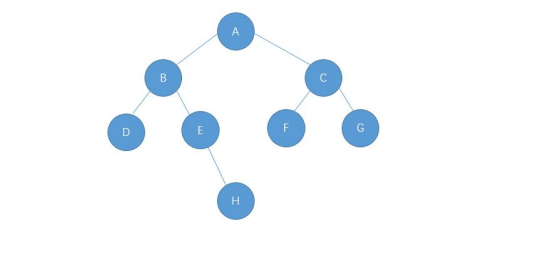
② Preorder traversal
graphic
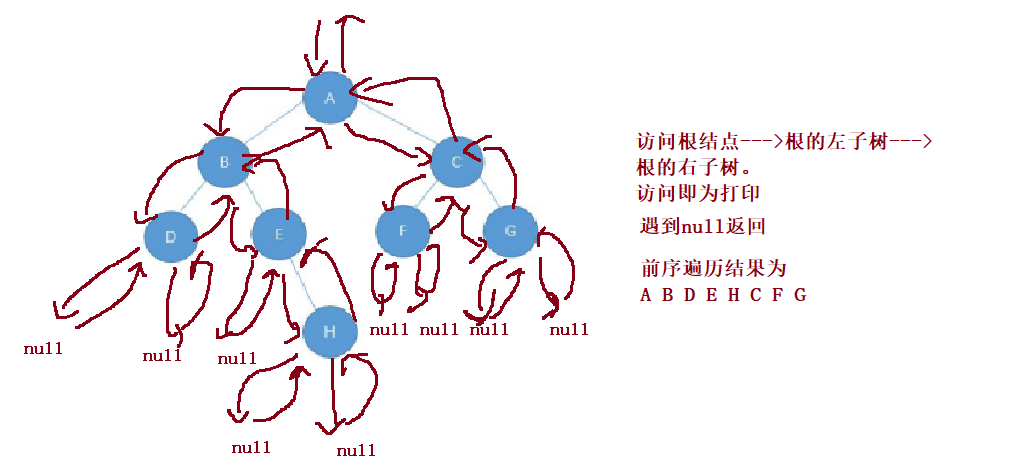
code analysis
We use enumeration to create this binary tree
public TreeNode createTree() {
TreeNode A = new TreeNode('A');
TreeNode B = new TreeNode('B');
TreeNode C = new TreeNode('C');
TreeNode D = new TreeNode('D');
TreeNode E = new TreeNode('E');
TreeNode F = new TreeNode('F');
TreeNode G = new TreeNode('G');
TreeNode H = new TreeNode('H');
A.left = B;
A.right = C;
B.left = D;
B.right = E;
C.left = F;
C.right = G;
E.right = H;
return A;
}// Preorder traversal
void preOrderTraversal(TreeNode root){
if(root == null) {
return;
}
System.out.print(root.val+" ");
preOrderTraversal(root.left);
preOrderTraversal(root.right);
}
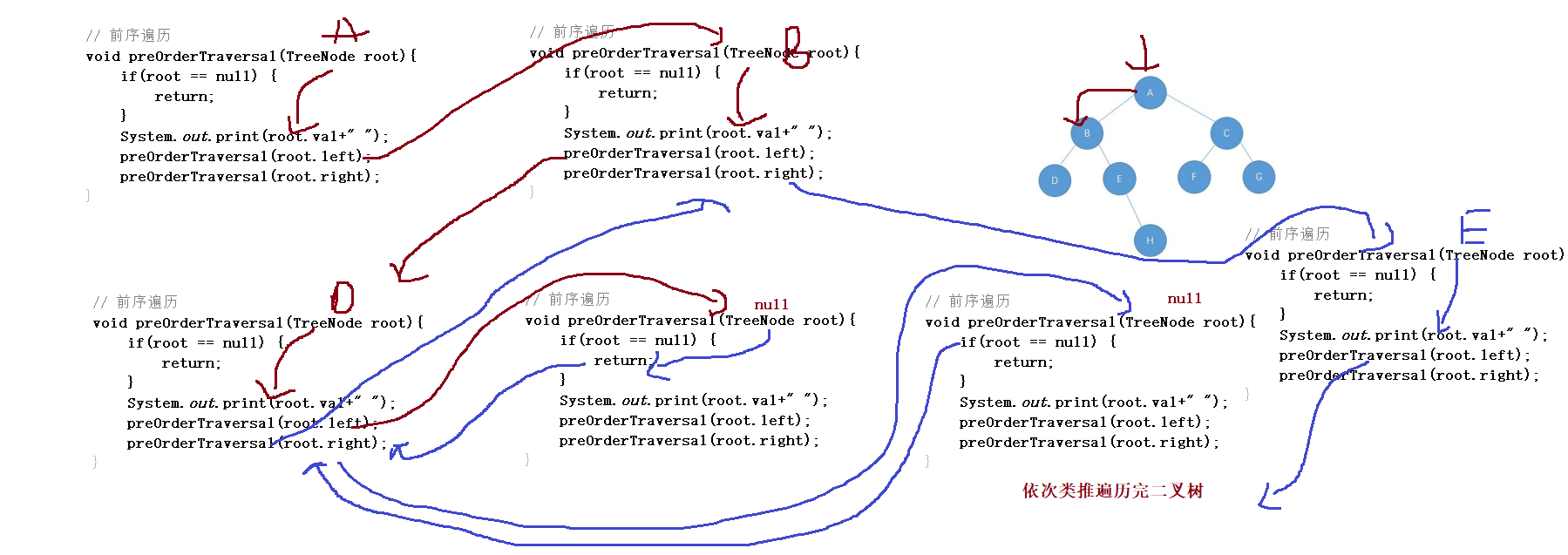
DeBug analysis
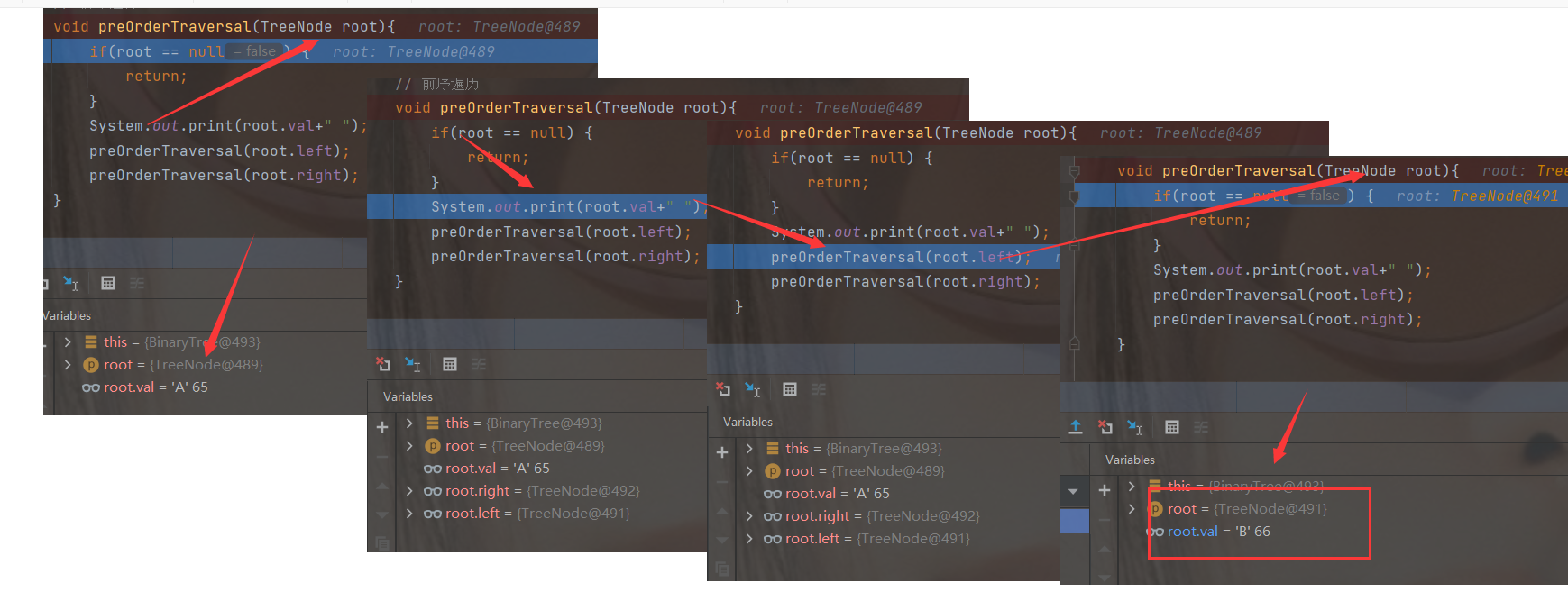③ Medium order traversal
graphic
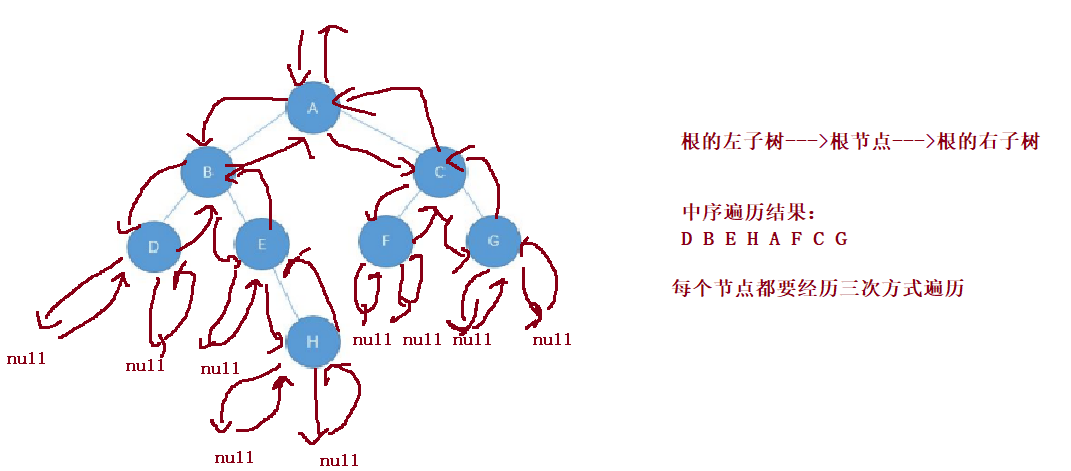
// Medium order traversal
void inOrderTraversal(TreeNode root){
if(root == null) {
return;
}
inOrderTraversal(root.left);
System.out.print(root.val+" ");
inOrderTraversal(root.right);
}
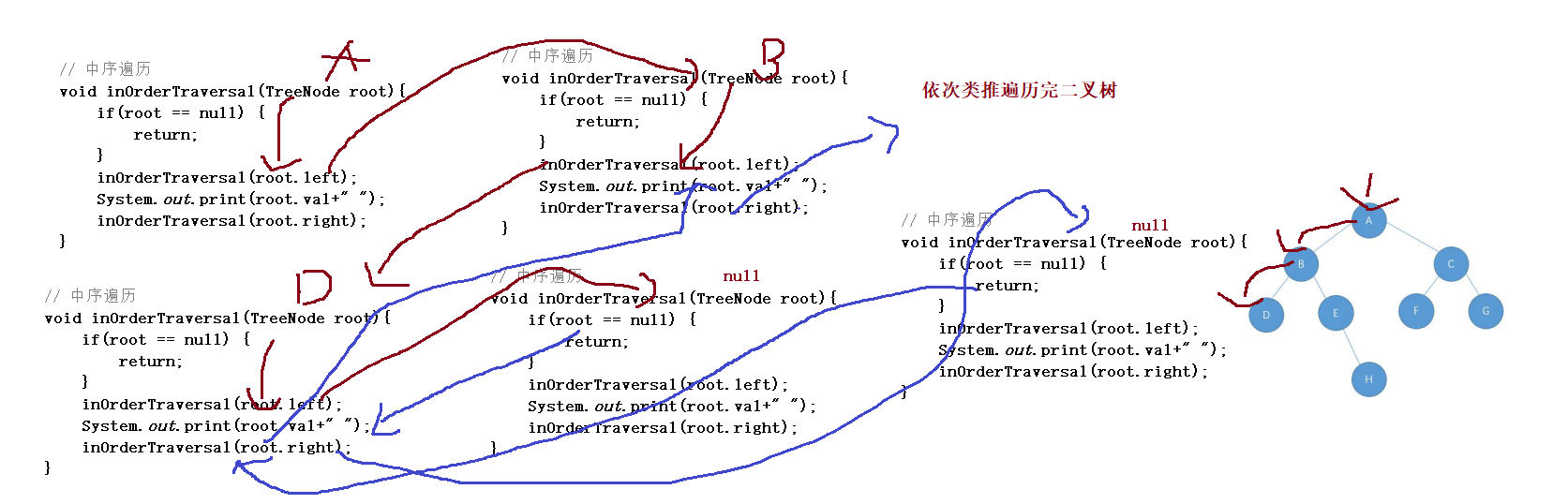
DeBug analysis
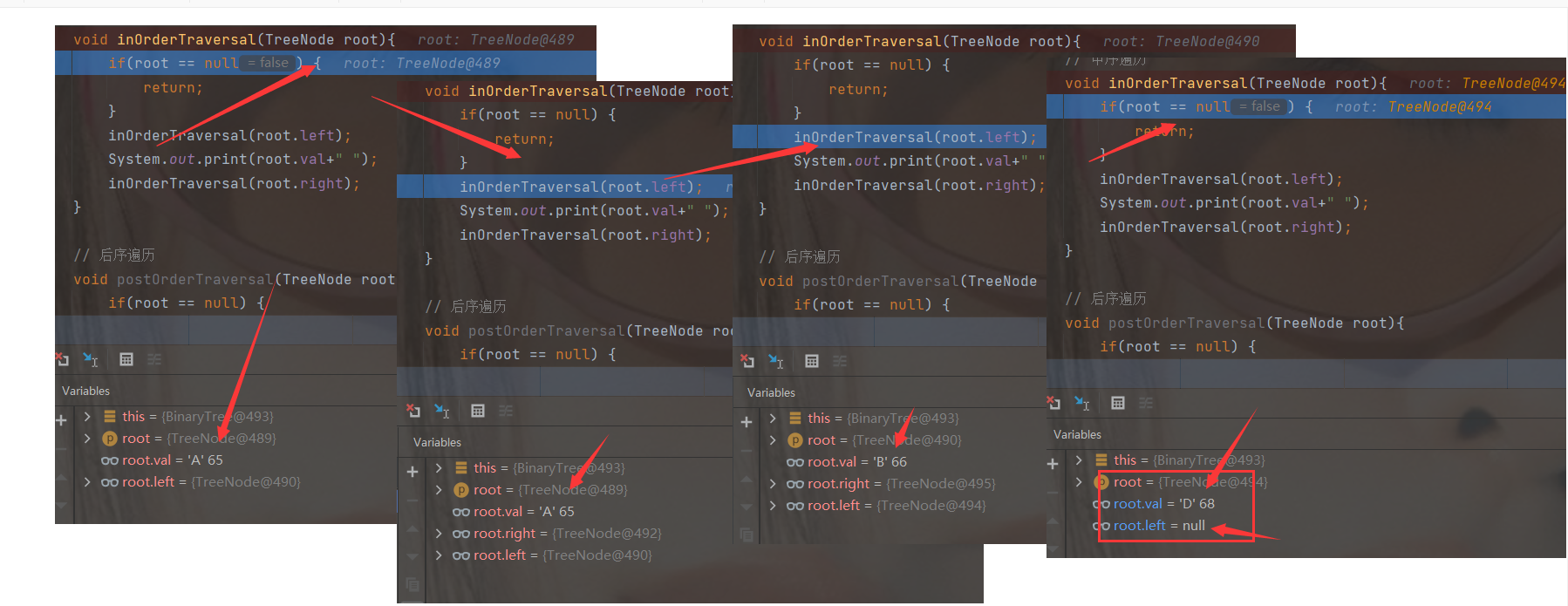
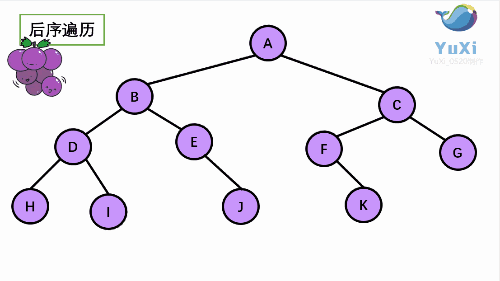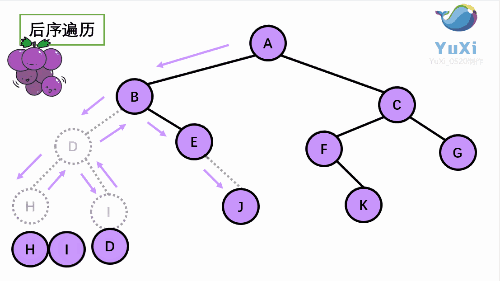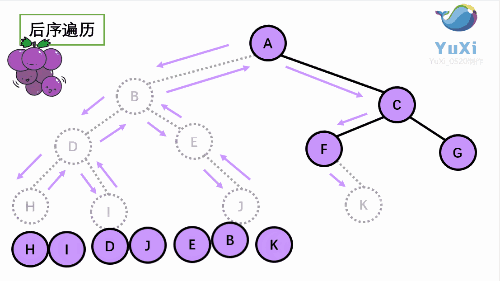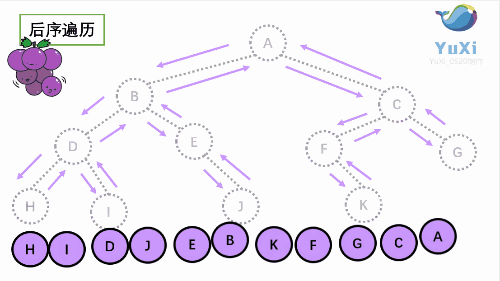
④ Postorder traversal
graphic
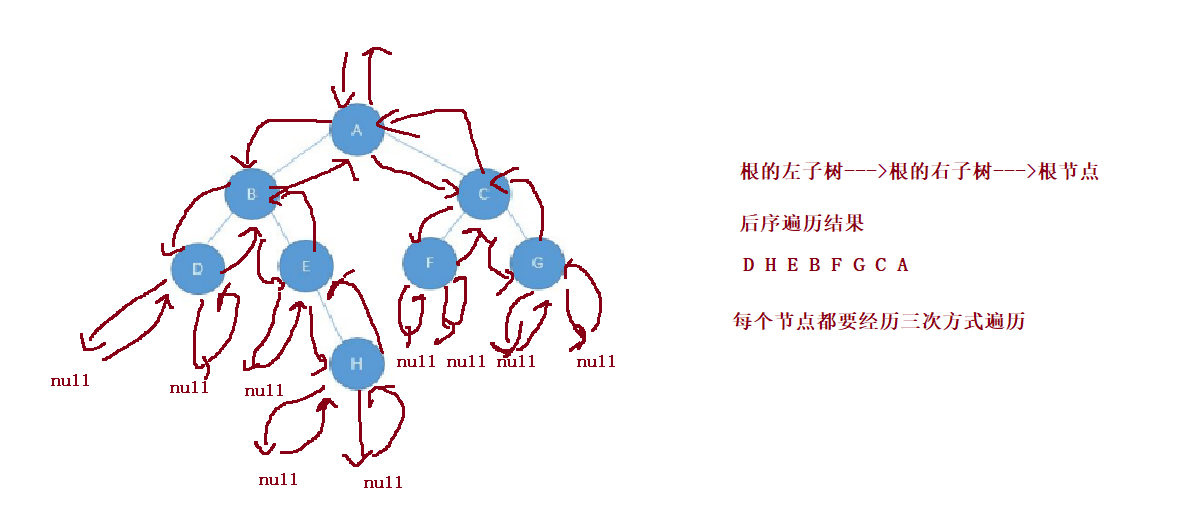
// Postorder traversal
void postOrderTraversal(TreeNode root){
if(root == null) {
return;
}
postOrderTraversal(root.left);
postOrderTraversal(root.right);
System.out.print(root.val+" ");
}
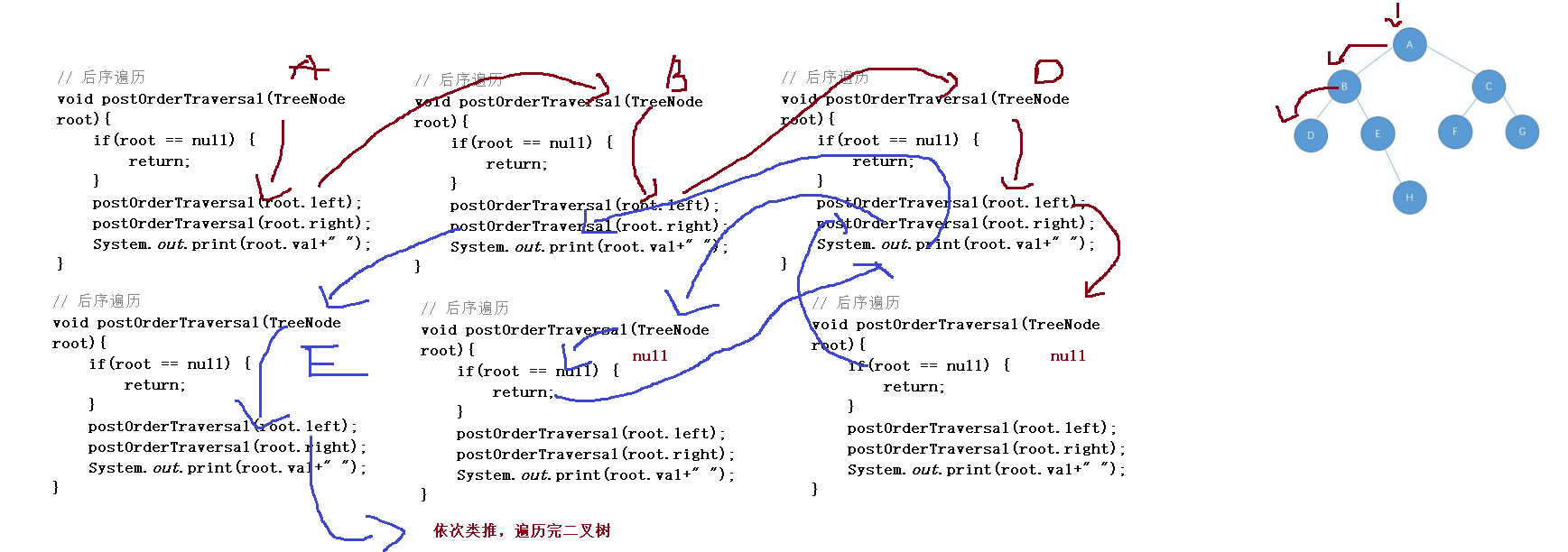
DeBug analysis
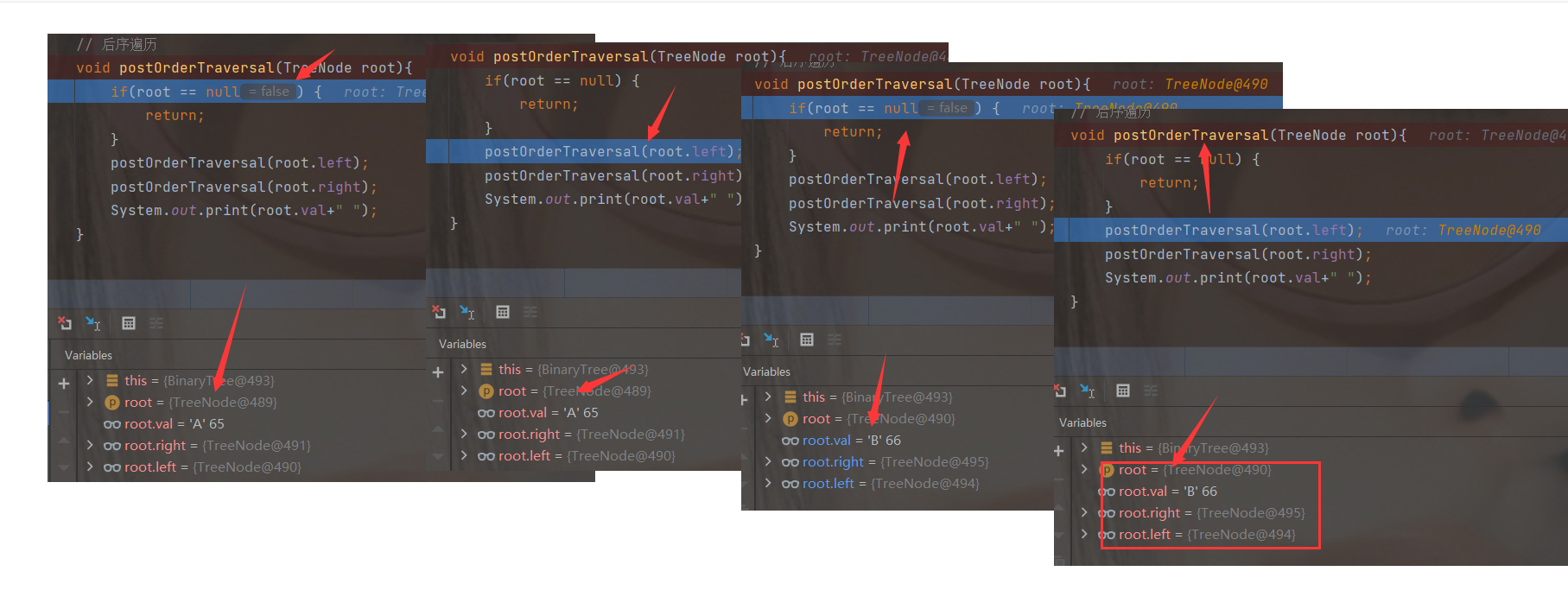
3. Binary search tree
① Concept
Binary search tree is also called binary sort tree. It is either an empty tree * * or a tree with the following properties Binary tree:
If its left subtree is not empty, the values of all nodes on the left subtree are less than those of the root node
If its right subtree is not empty, the values of all nodes on the right subtree are greater than those of the root node
Its left and right subtrees are also binary search trees
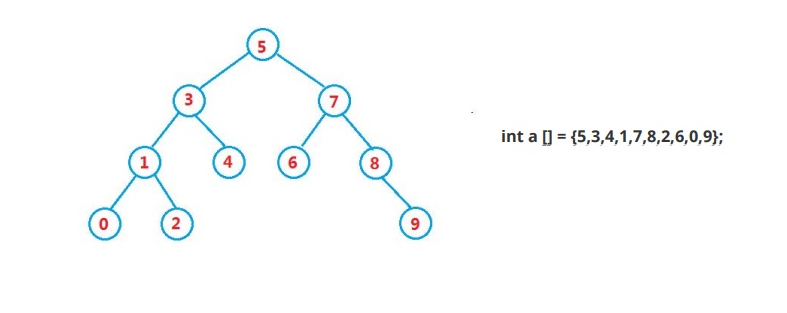
② Action - find
Binary search tree The lookup for is similar to the dichotomy lookup
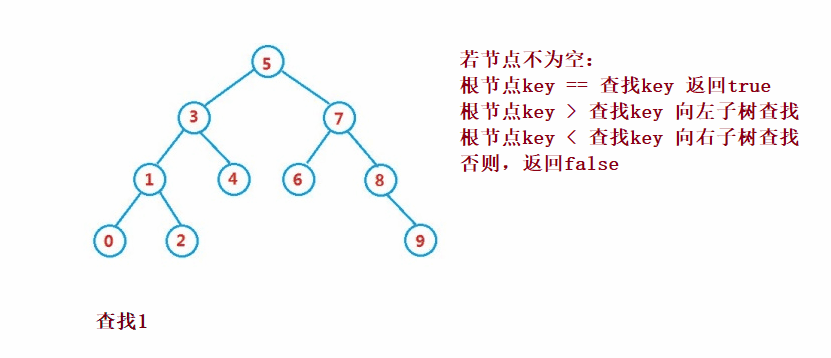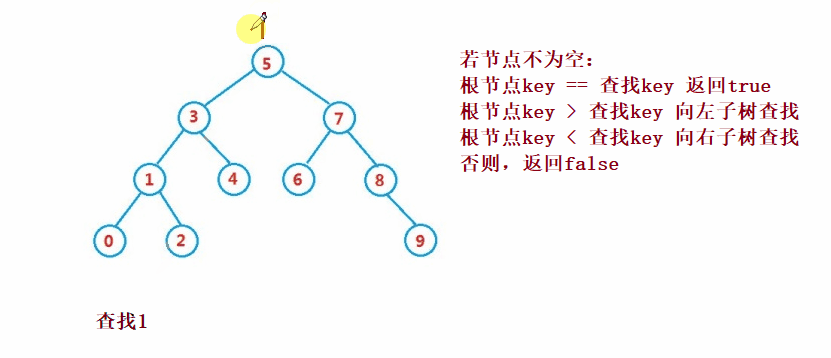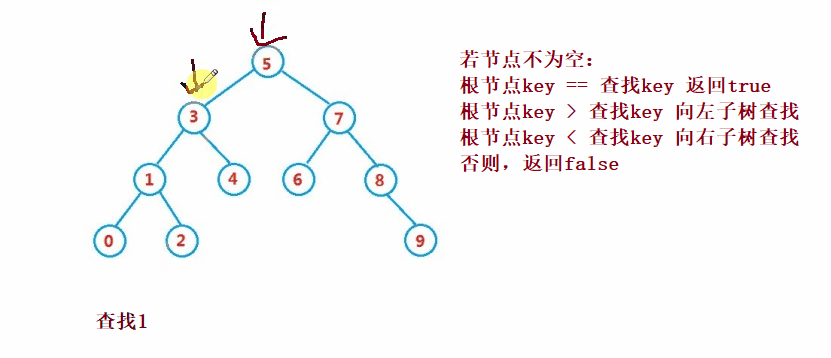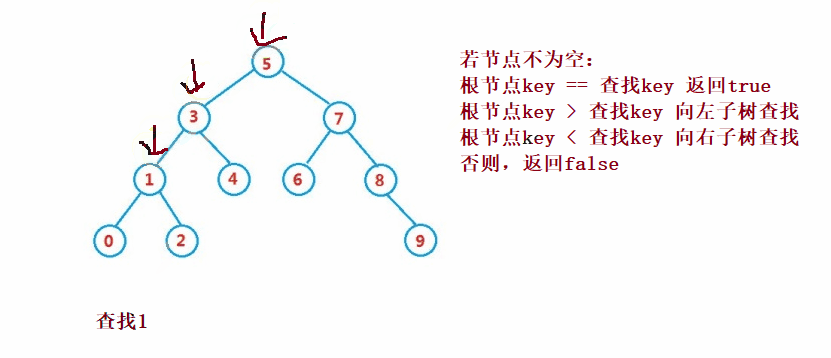
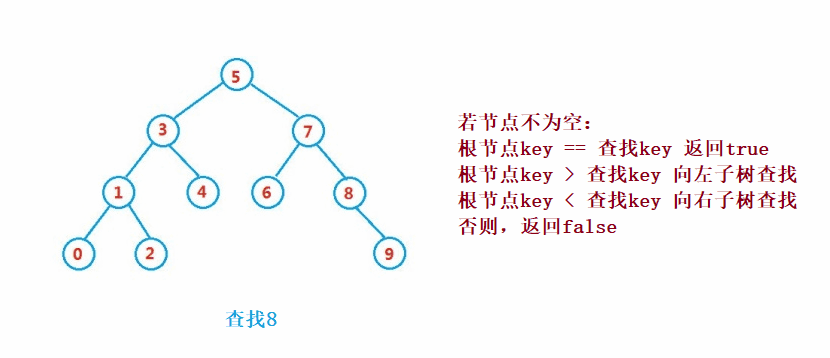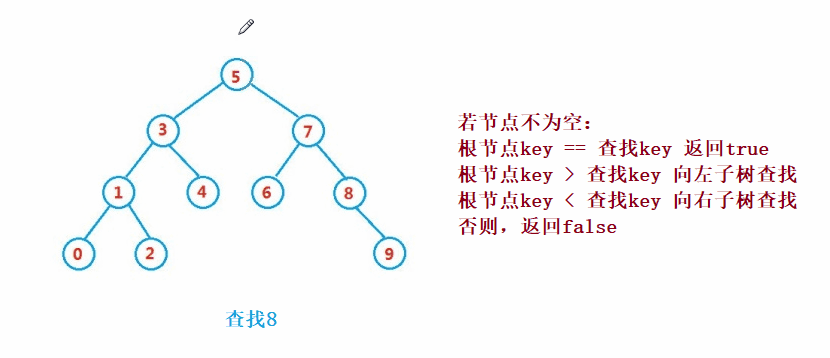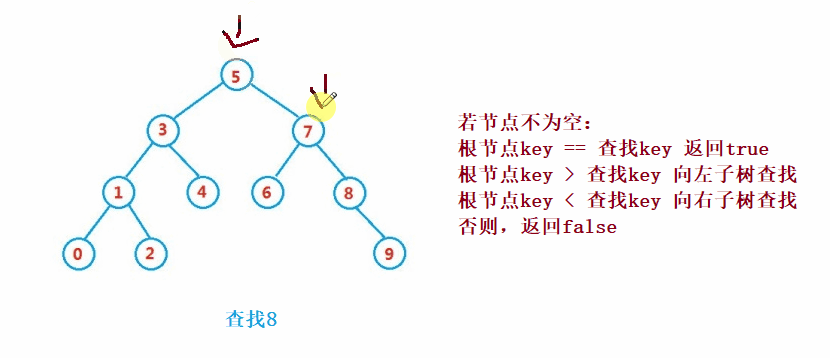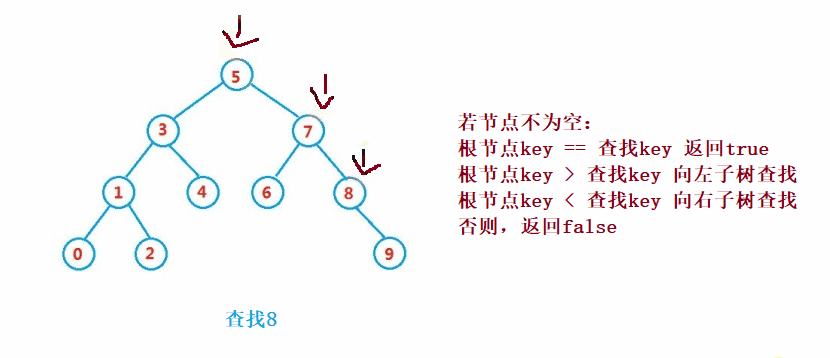
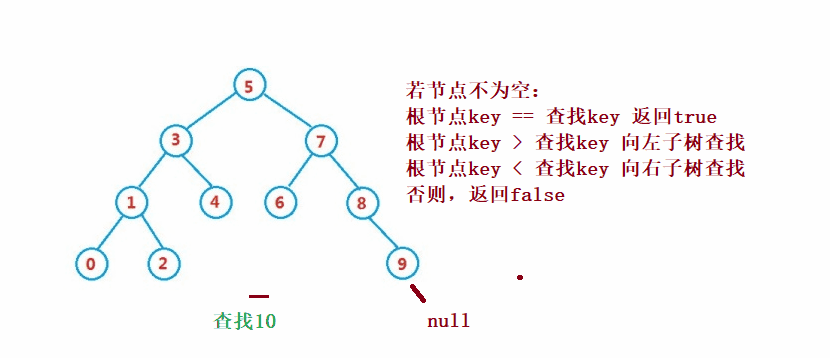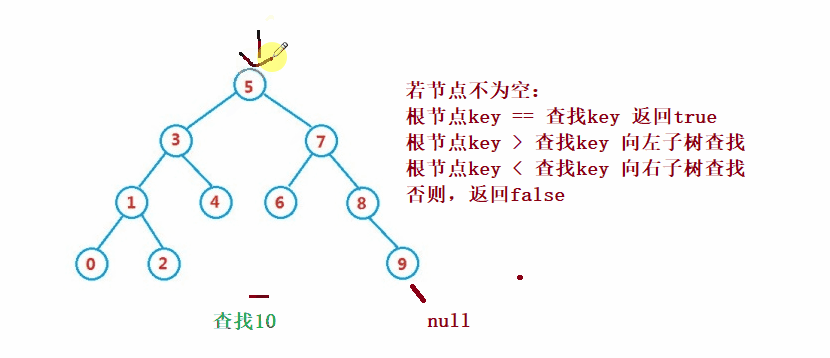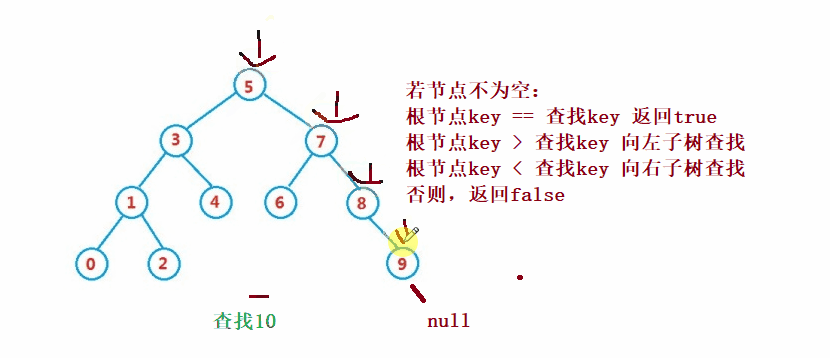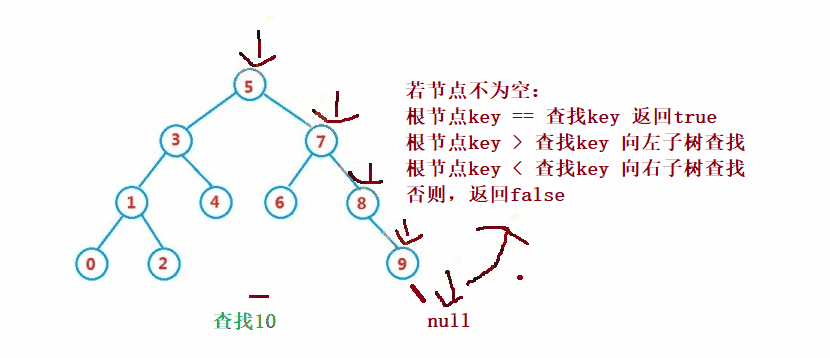
public Node search(int key) {
Node cur = root;
while (cur != null) {
if(cur.val == key) {
return cur;
}else if(cur.val < key) {
cur = cur.right;
}else {
cur = cur.left;
}
}
return null;
}③ Operation - insert
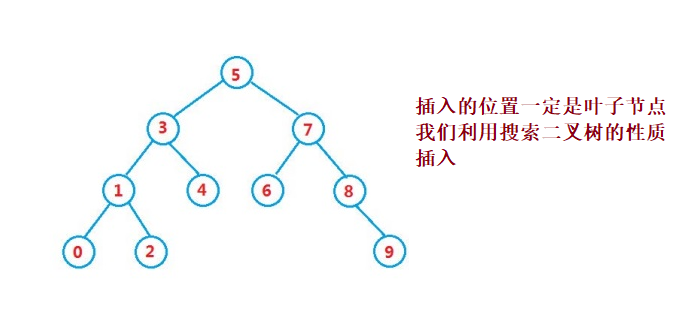
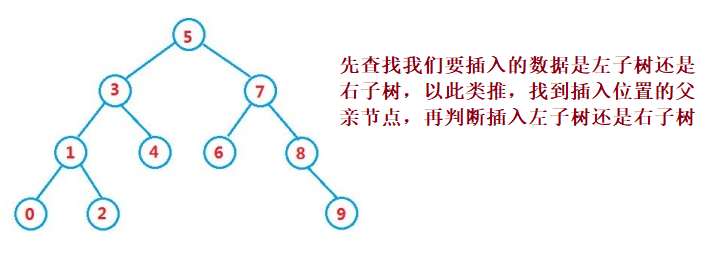
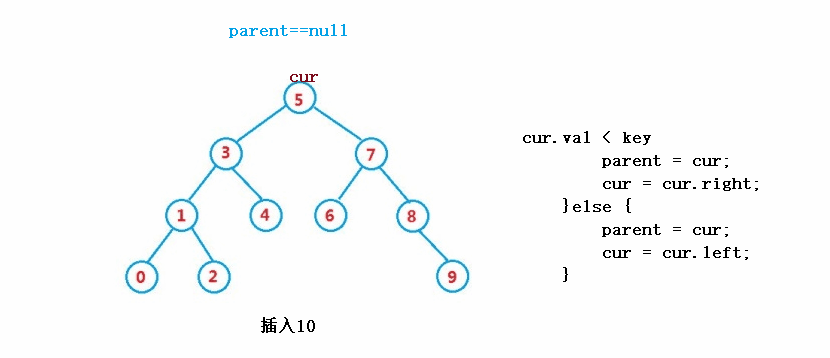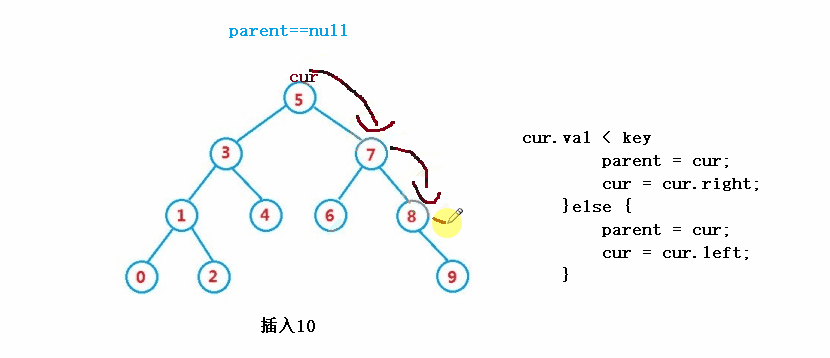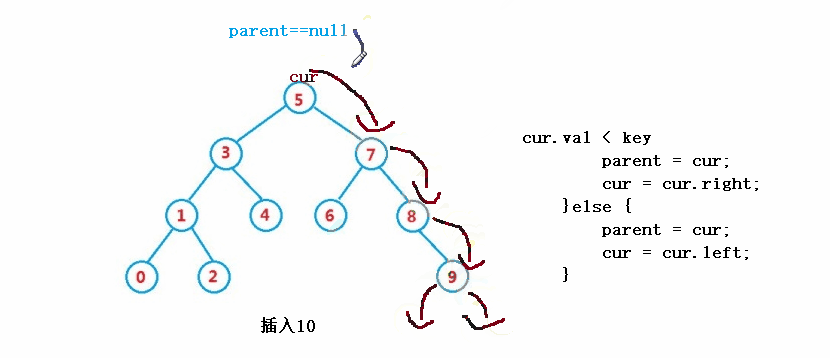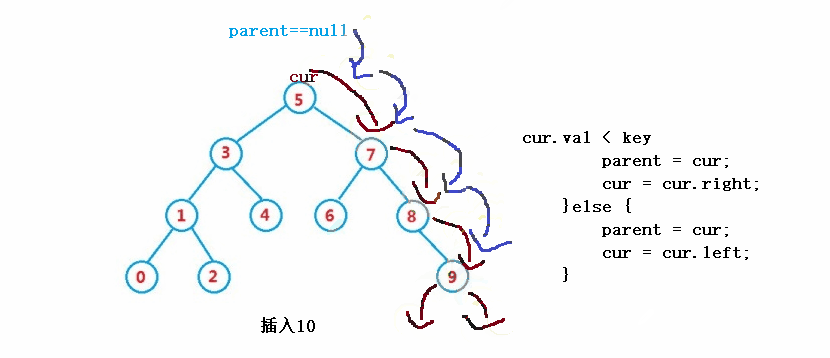
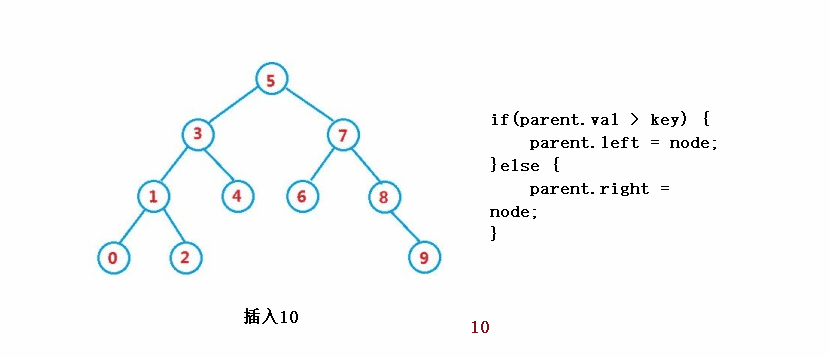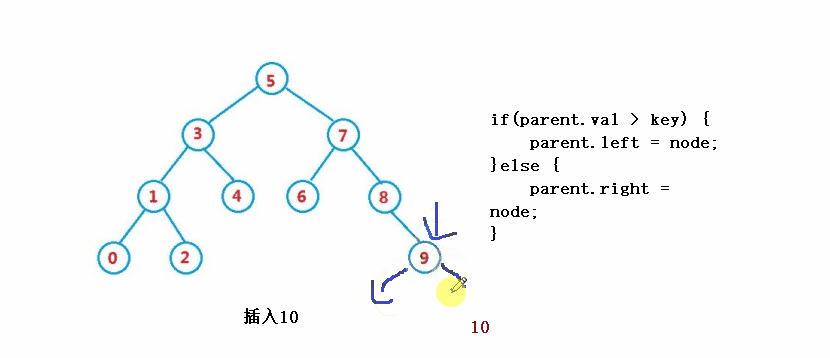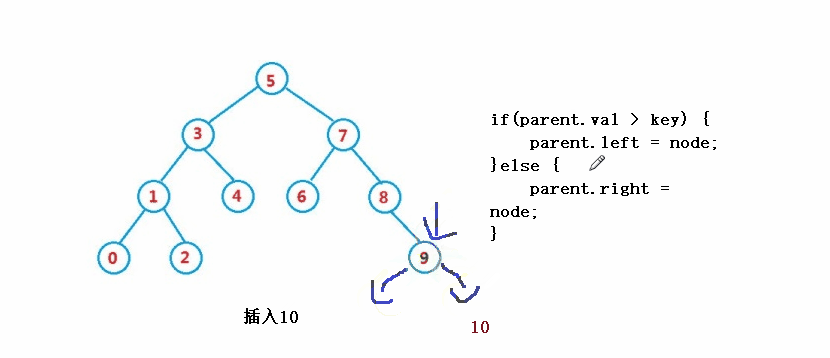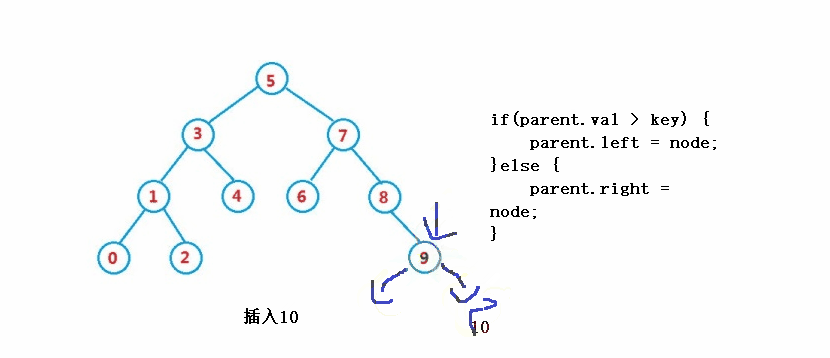
public boolean insert(int key) {
Node node = new Node(key);
if(root == null) {
root = node;
return true;
}
Node cur = root;
Node parent = null;
while(cur != null) {
if(cur.val == key) {
return false;
}else if(cur.val < key) {
parent = cur;
cur = cur.right;
}else {
parent = cur;
cur = cur.left;
}
}
//parent
if(parent.val > key) {
parent.left = node;
}else {
parent.right = node;
}
return true;
}④ operation - delete
The deletion operation is complex, but it is easy to understand its principle
Set the node to be deleted as cur and the parent node of the node to be deleted as parent
1. cur.left == null
1. If cur is root, then root = cur right
2. cur is not root, but cur is parent Left, then parent left = cur. right
3. cur is not root, but cur is parent Right, then parent right = cur. right
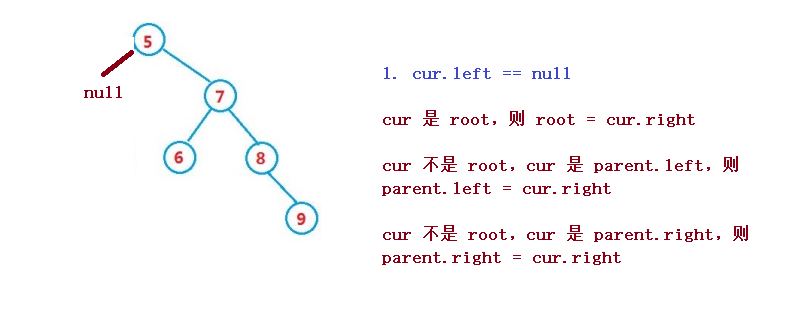
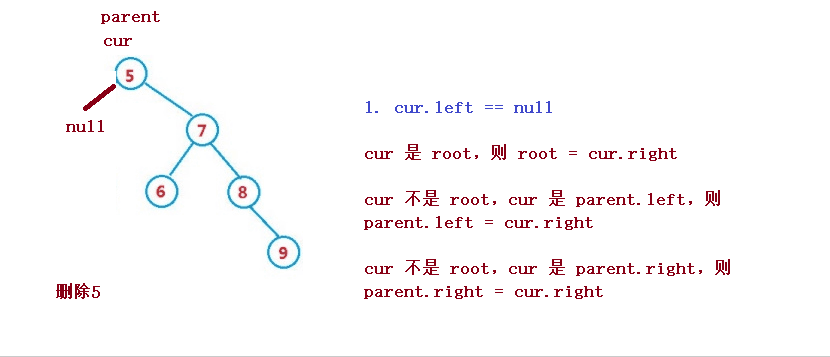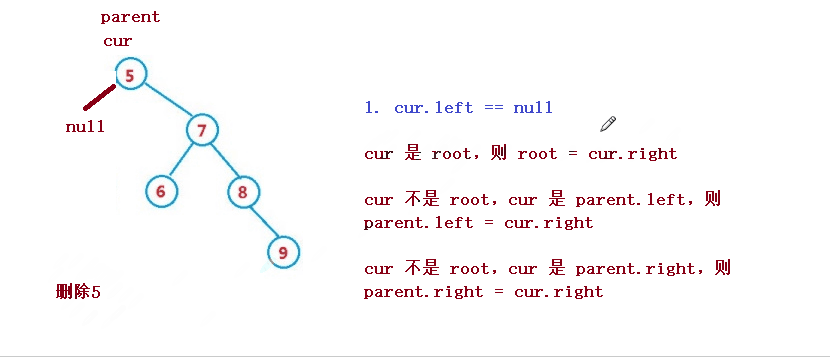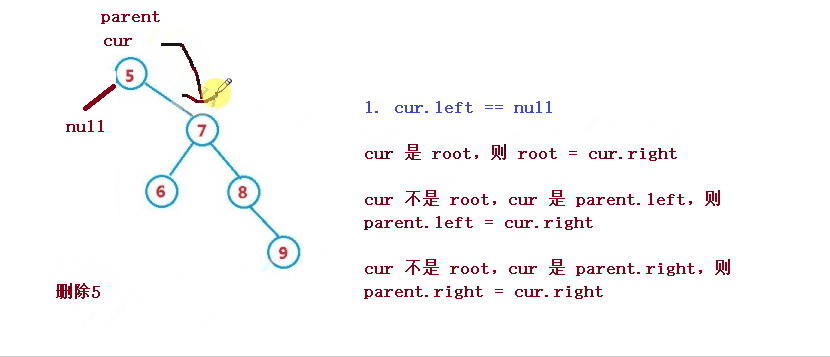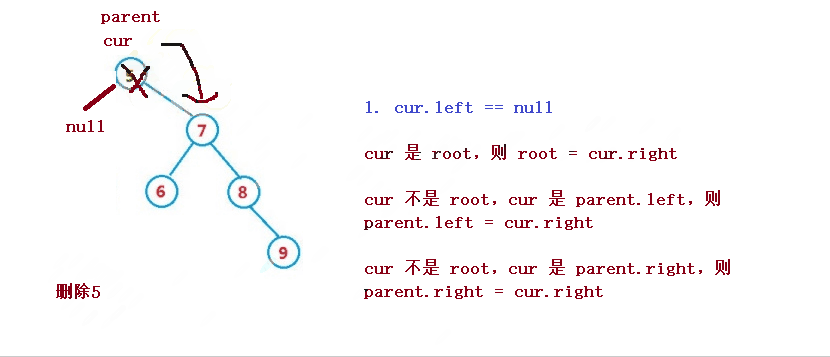
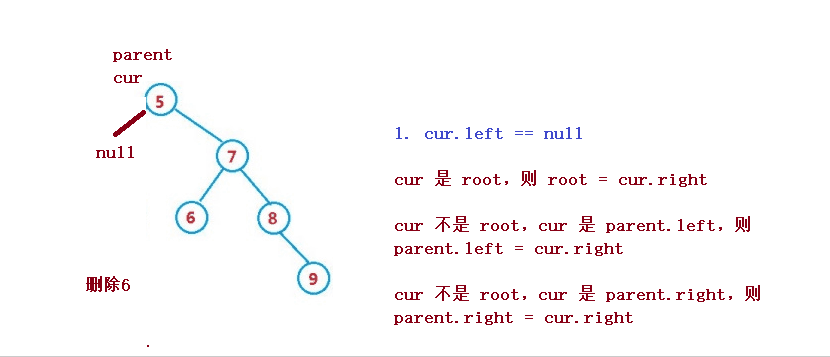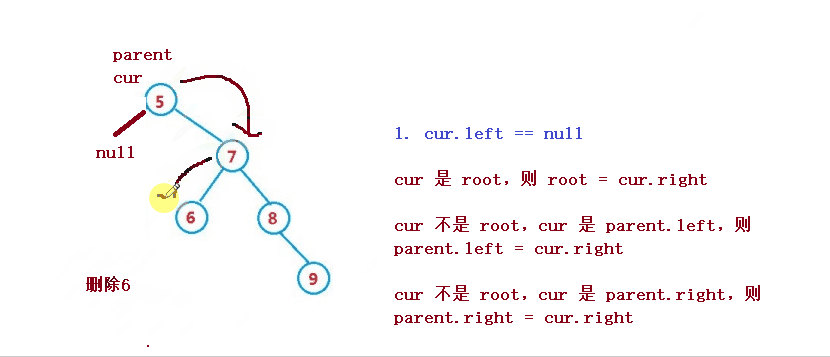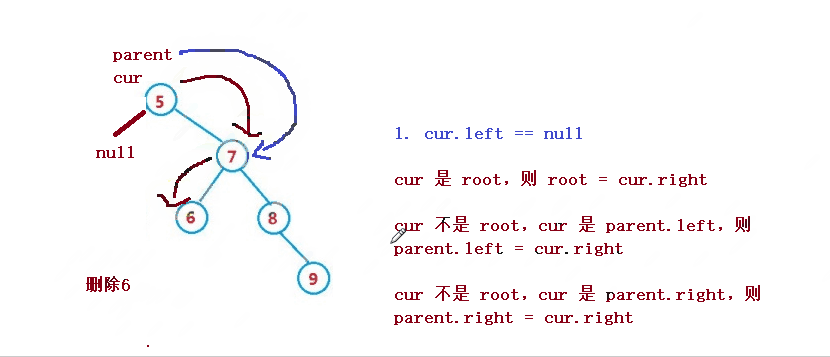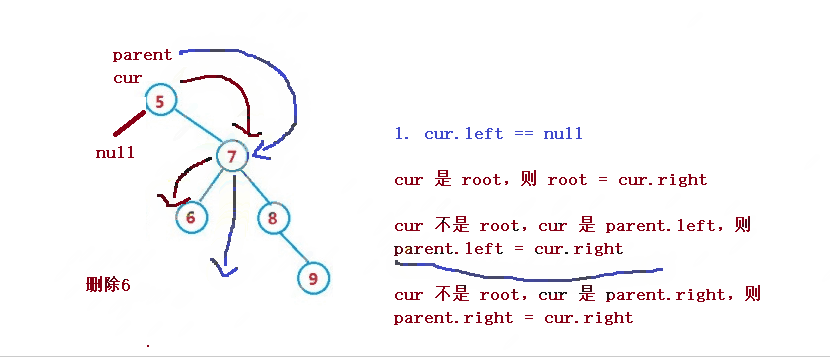
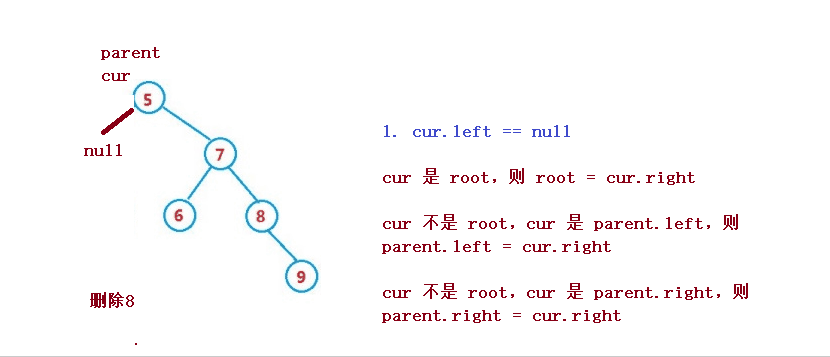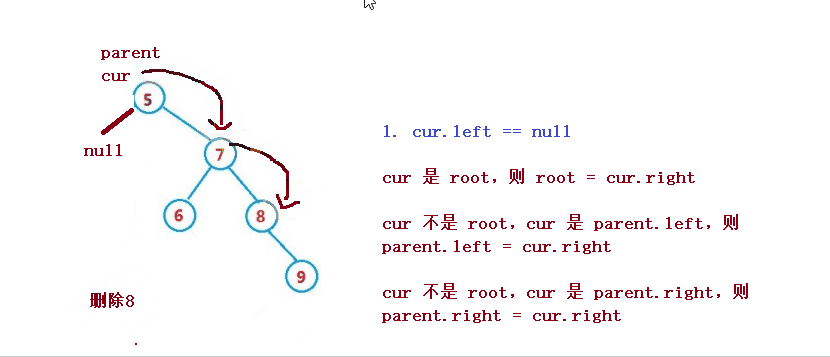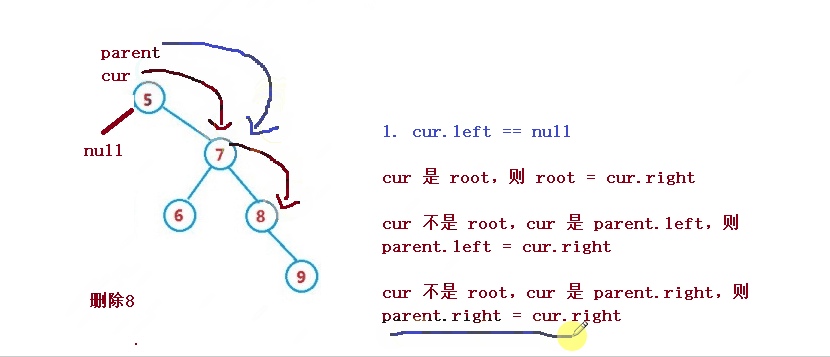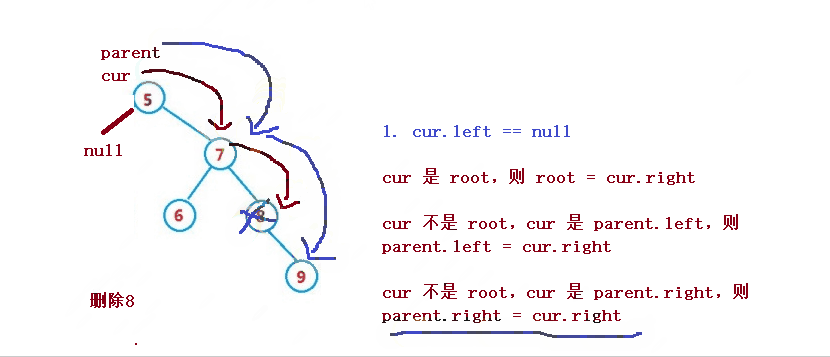
2. cur.right == null
1. If cur is root, then root = cur left
2. cur is not root, but cur is parent Left, then parent left = cur. left
3. cur is not root, but cur is parent Right, then parent right = cur. left
The second case is the same as the first case, but in the opposite direction. There is no drawing here
3. cur.left != null && cur.right != null
The replacement method needs to be used for deletion, that is, find the first node in the middle order in its right subtree (with the smallest key), fill its value into the deleted node, and then deal with the deletion of the node
When we delete when the left and right subtrees are not empty, deleting the node will destroy the tree structure. Therefore, we use the scapegoat method to solve the problem. The actual deletion process is still the above two cases, and the nature of search binary tree is used here
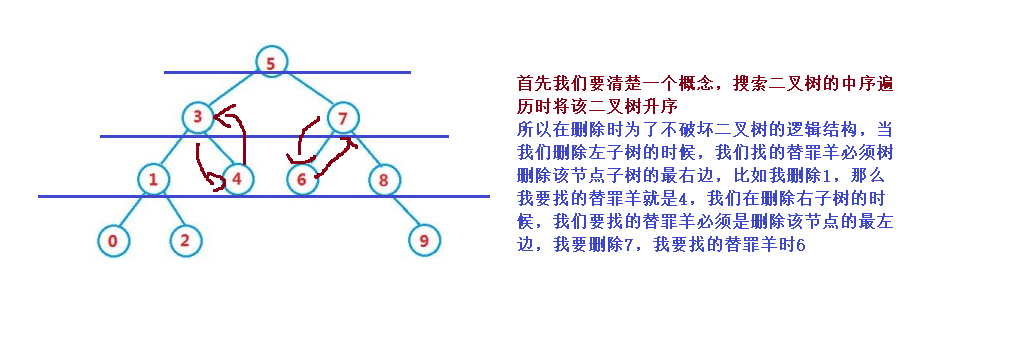
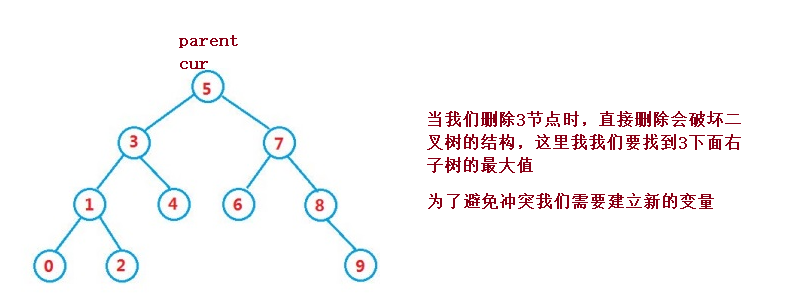
public void remove(Node parent,Node cur) {
if(cur.left == null) {
if(cur == root) {
root = cur.right;
}else if(cur == parent.left) {
parent.left = cur.right;
}else {
parent.right = cur.right;
}
}else if(cur.right == null) {
if(cur == root) {
root = cur.left;
}else if(cur == parent.left) {
parent.left = cur.left;
}else {
parent.right = cur.left;
}
}else {
Node targetParent = cur;
Node target = cur.right;
while (target.left != null) {
targetParent = target;
target = target.left;
}
cur.val = target.val;
if(target == targetParent.left) {
targetParent.left = target.right;
}else {
targetParent.right = target.right;
}
}
}
public void removeKey(int key) {
if(root == null) {
return;
}
Node cur = root;
Node parent = null;
while (cur != null) {
if(cur.val == key) {
remove(parent,cur);
return;
}else if(cur.val < key){
parent = cur;
cur = cur.right;
}else {
parent = cur;
cur = cur.left;
}
}
}⑤ Performance analysis
Both insert and delete operations must be searched first. The search efficiency represents the performance of each operation in the binary search tree.
For a binary search tree with n nodes, if the search probability of each element is equal, the average search length of the binary search tree is a function of the depth of the node in the binary search tree, that is, the deeper the node, the more comparisons.
However, for the same key set, if the insertion order of each key is different, binary search trees with different structures may be obtained
In the optimal case, the binary search tree is a complete binary tree, and its average comparison times are: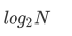
In the worst case, the binary search tree degenerates into a single branch tree, and its average comparison times are:
4. Written test exercises
① Preorder traversal of binary tree
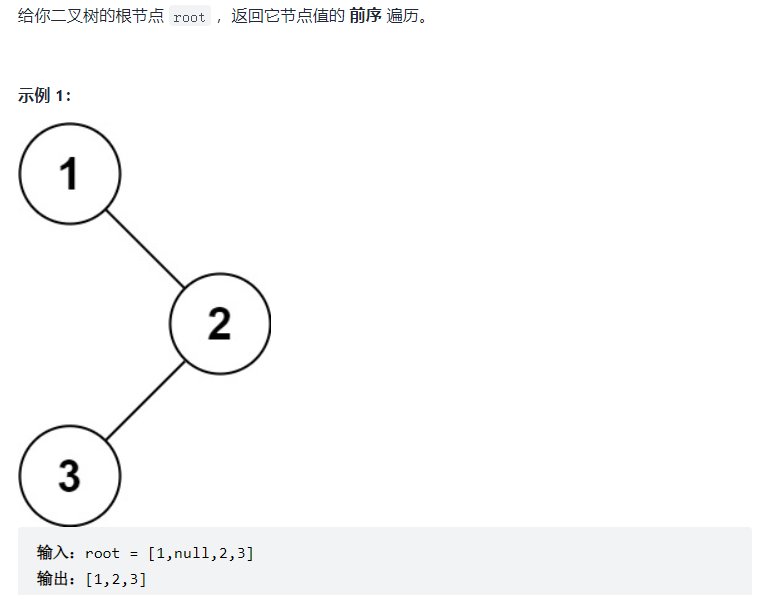
void preOrderTraversal(TreeNode root){
if(root == null) {
return;
}
System.out.print(root.val+" ");
preOrderTraversal(root.left);
preOrderTraversal(root.right);
}② Order traversal in binary tree
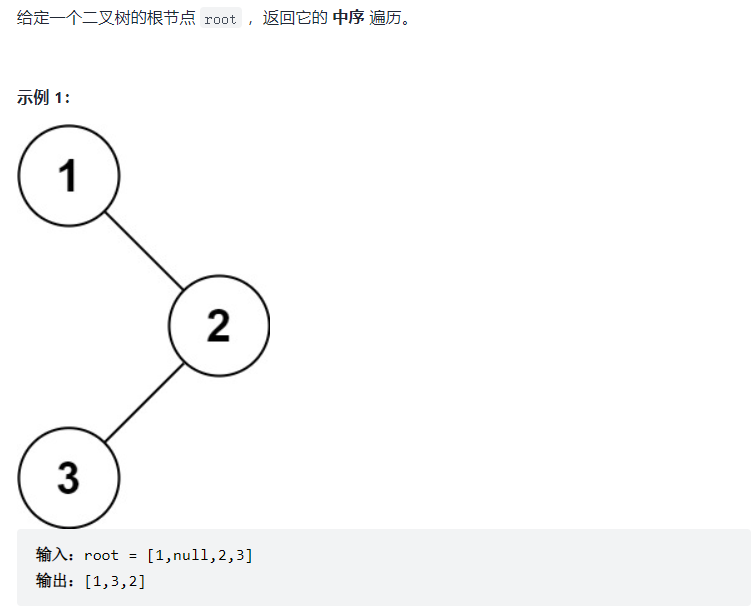
void inOrderTraversal(TreeNode root){
if(root == null) {
return;
}
inOrderTraversal(root.left);
System.out.print(root.val+" ");
inOrderTraversal(root.right);
}③ Postorder traversal of binary tree
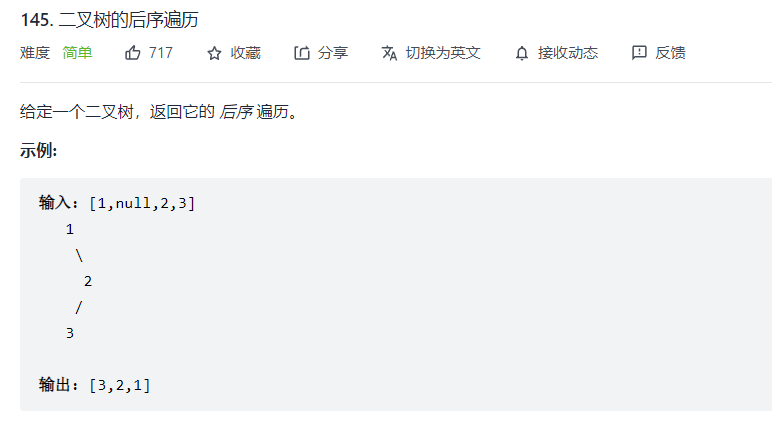
void postOrderTraversal(TreeNode root){
if(root == null) {
return;
}
postOrderTraversal(root.left);
postOrderTraversal(root.right);
System.out.print(root.val+" ");
}④ Check whether the two trees are the same
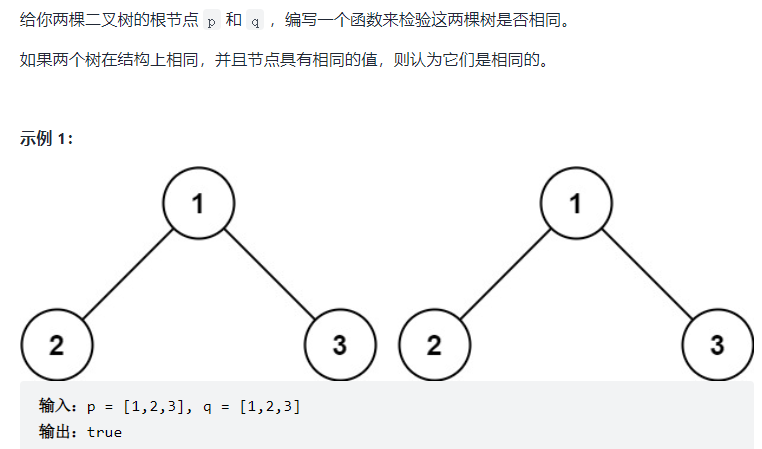
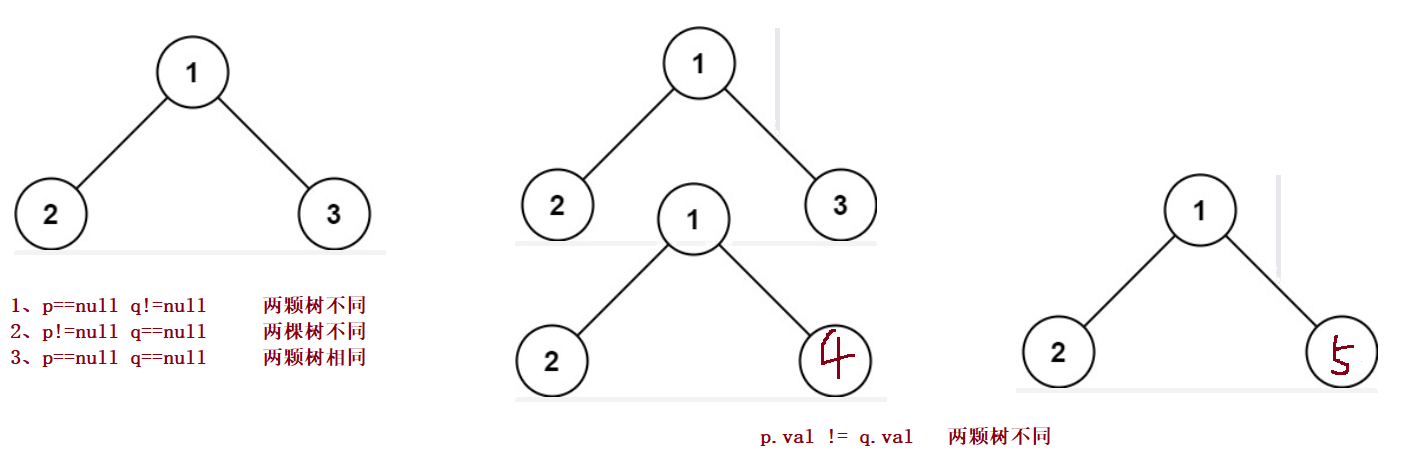
public boolean isSameTree(TreeNode p,TreeNode q){
if(p == null && q != null){
return false;
}
if(p != null && q == null){
return false;
}
if(p == null && q ==null){
return true;
}
if(p.val != q.val){
return false;
}
return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
}
⑤ Maximum depth of binary tree
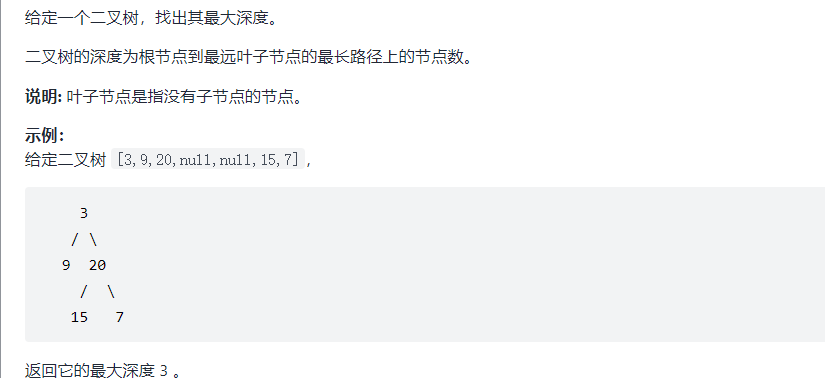
public int maxDepth(TreeNode root){
if(root == null){
return 0;
}
int leftHeight = maxDepth(root.left);
int rightHeight = maxDepth(root.right);
return Math.abs(leftHeight-rightHeight > 0? leftHeight + 1: rightHeight + 1);
}⑥ A subtree of another tree
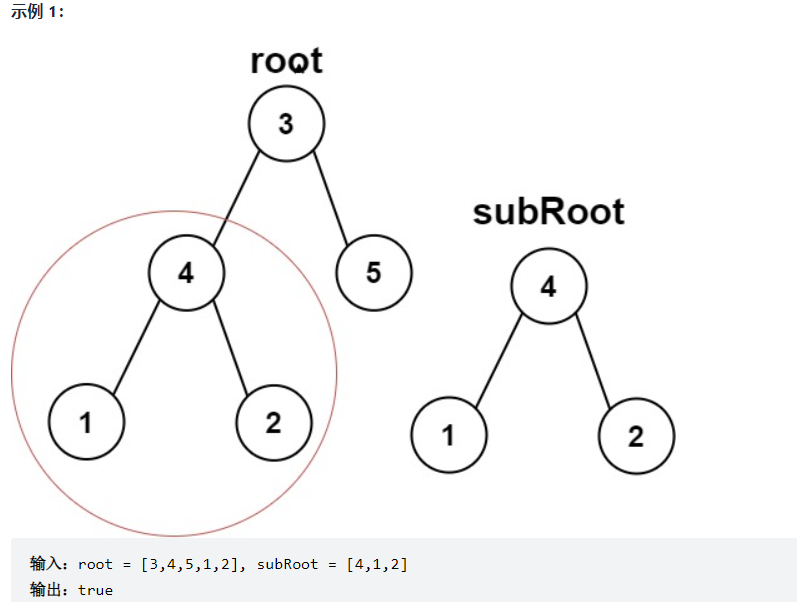
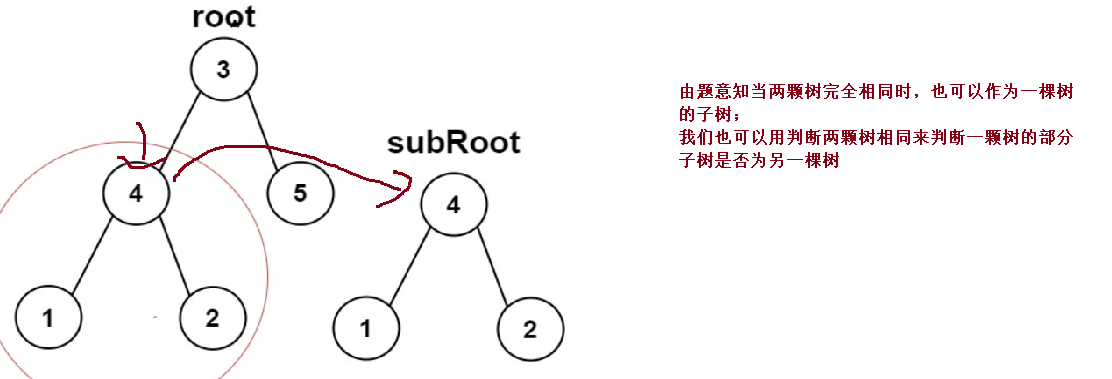
public boolean isSameTree(TreeNode p,TreeNode q){
if(p == null && q != null){
return false;
}
if(p != null && q == null){
return false;
}
if(p == null && q ==null){
return true;
}
if(p.val != q.val){
return false;
}
return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
}
public boolean isSubtree(TreeNode root, TreeNode suBroot){
if(root == null && suBroot == null){
return true;
}
if(isSameTree(root,suBroot)){
return true;
}
if(isSubtree(root.right,suBroot)){
return true;
}
if(isSubtree(root.left,suBroot)){
return true;
}
return false;
}⑦ Judge whether a tree is a balanced binary tree
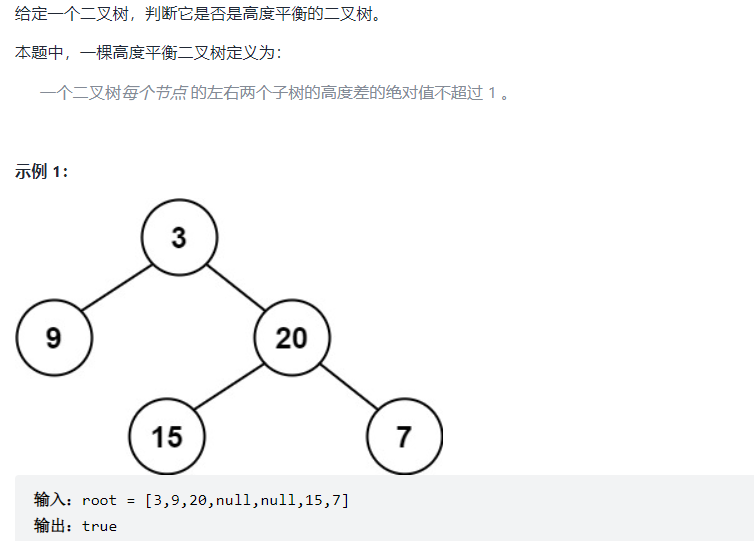
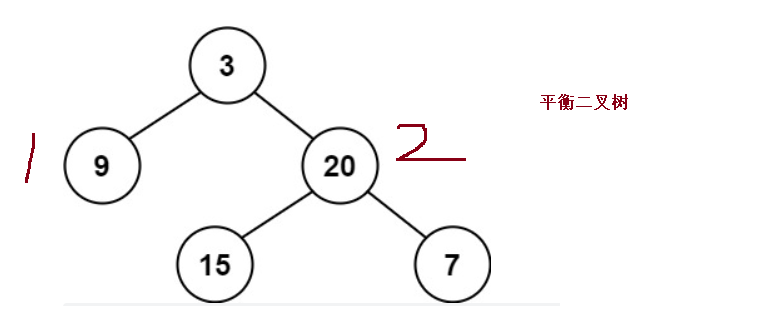
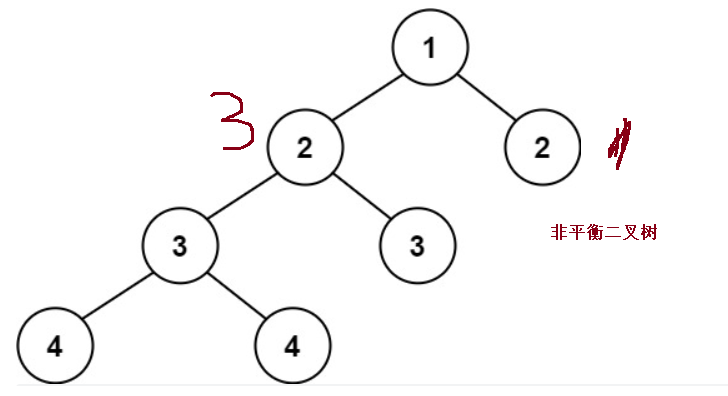
public int maxDepth(TreeNode root){
if(root == null){
return 0;
}
int leftHeight = maxDepth(root.left);
int rightHeight = maxDepth(root.right);
return Math.abs(leftHeight-rightHeight > 0? leftHeight + 1: rightHeight + 1);
}
public boolean isBalanced(TreeNode root) {
if(root == null) {
return true;
}
int leftHeight = maxDepth(root.left);
int rightHeight = maxDepth(root.right);
return
Math.abs(leftHeight-rightHeight) < 2 && isBalanced(root.left) && isBalanced(root.right);
}
public int hight(TreeNode root){
if(root == null){
return 0;
}
int leftHeight = hight(root.left);
int rightHeight = hight(root.right);
if(leftHeight >= 0 && rightHeight >= 0 && Math.abs(leftHeight-rightHeight) <= 1){
return Math.max(leftHeight,rightHeight)+1;
}else{
return -1;
}
}
public boolean isBalanced2(TreeNode root) {
return hight(root) >= 0;
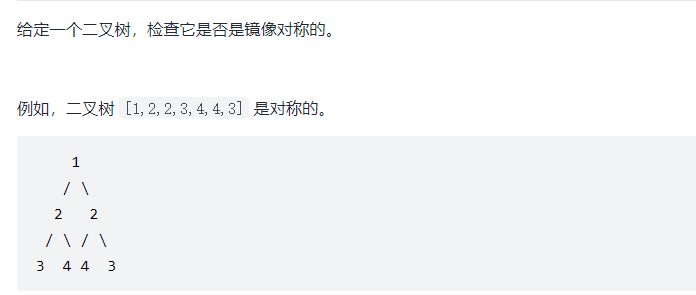
}⑧ Symmetric binary tree
public boolean isSymmetricChild(TreeNode leftTree,TreeNode rightTree){
if(leftTree != null && rightTree == null){
return false;
}
if(leftTree == null && rightTree != null){
return false;
}
if(leftTree == null && rightTree == null){
return true;
}
if(leftTree.val != rightTree.val){
return false;
}
return isSymmetricChild(leftTree.left,rightTree.right) &&
isSymmetricChild(leftTree.left,rightTree.right);
}
public boolean isSymmetric(TreeNode root){
if(root == null){
return true;
}
return isSymmetricChild(root.left,root.right);
}⑨ Binary tree image
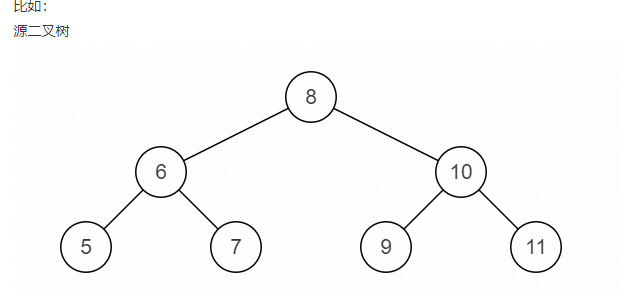
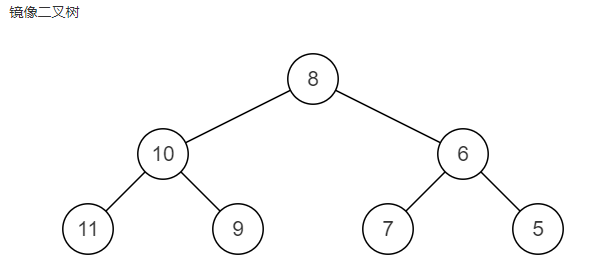
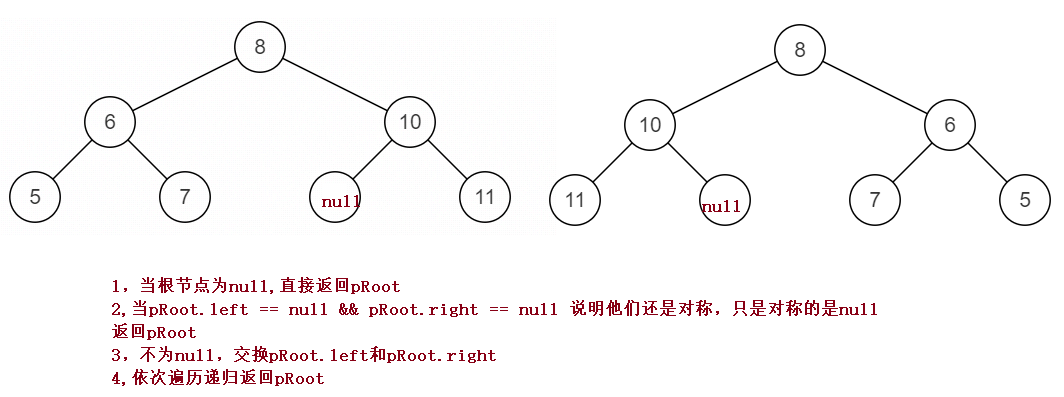
public TreeNode Mirror(TreeNode pRoot){
if(pRoot == null){
return pRoot;
}
if(pRoot.left == null && pRoot.right == null){
return pRoot;
}
TreeNode tmp = pRoot.left;
pRoot.left = pRoot.right;
pRoot.right = tmp;
if(pRoot.left != null){
Mirror(pRoot.left);
return pRoot;
}
if(pRoot.right != null){
Mirror(pRoot.right);
return pRoot;
}
return pRoot;
}5, Priority queue (heap)
1. Sequential storage of binary tree
① Storage mode
Use the array to save the binary tree structure, that is, the binary tree is put into the array by sequence traversal. Generally, it is only suitable for representing complete binary trees, because incomplete binary trees will waste space. The main use of this approach is the representation of the heap.
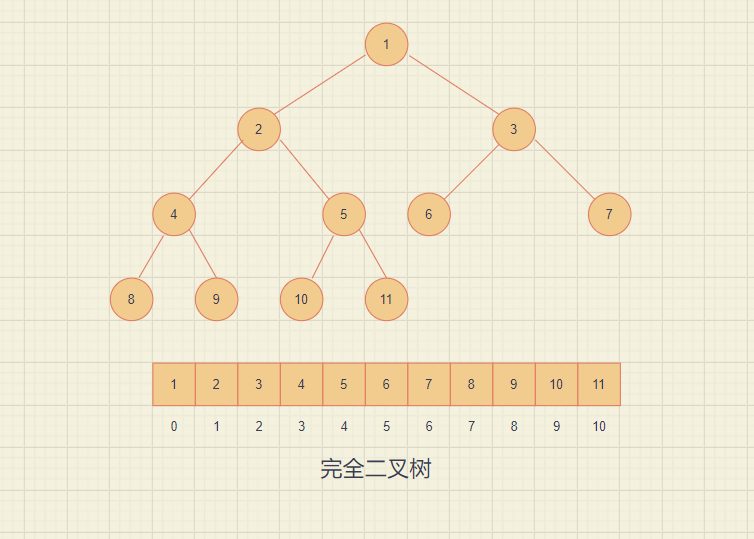
② Subscript relation
If the subscript of the parent is known, then:
Left subscript = 2 * parent + 1;
Right subscript = 2 * parent + 2;
If the child subscript is known, then:
Parent subscript = (child - 1) / 2;
③ Binary tree sequential traversal
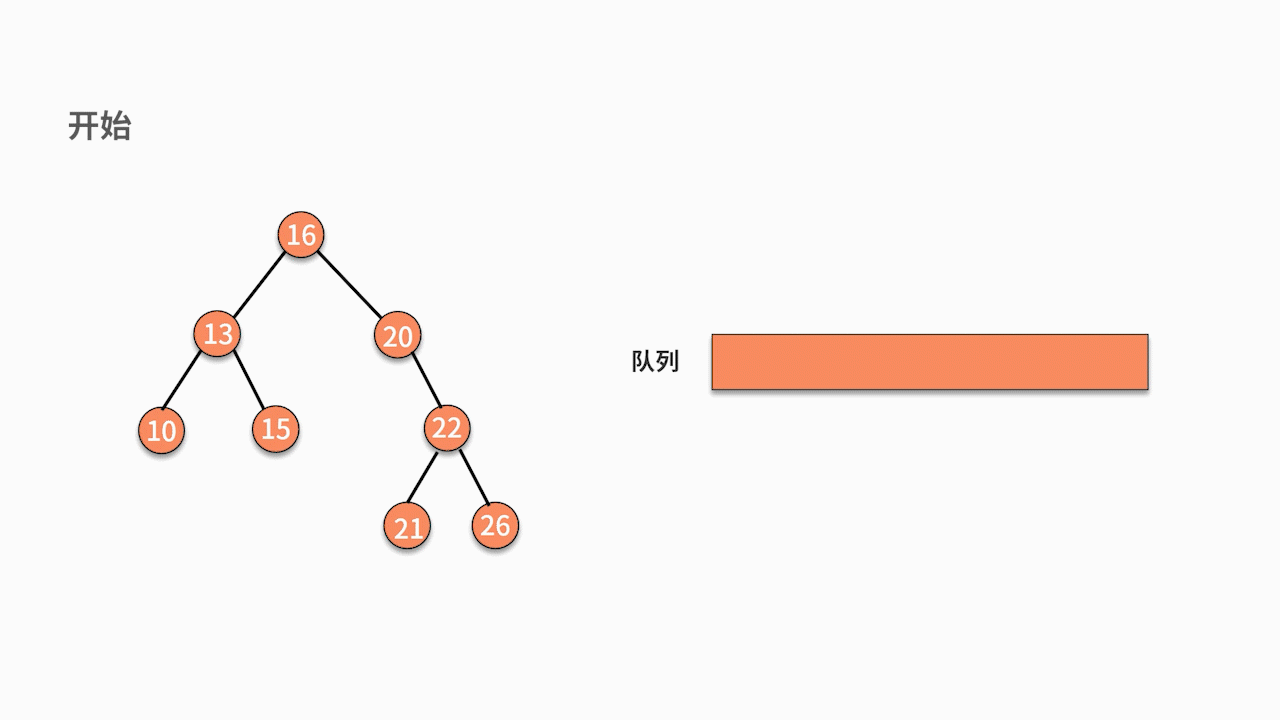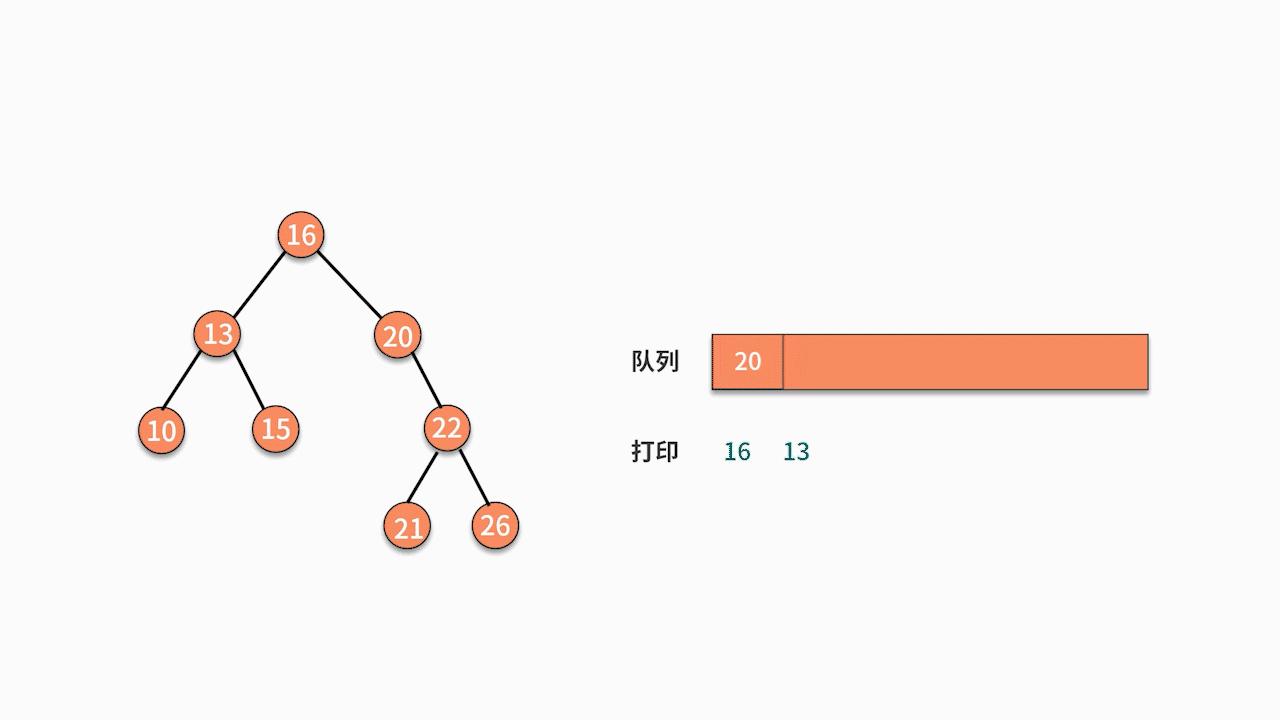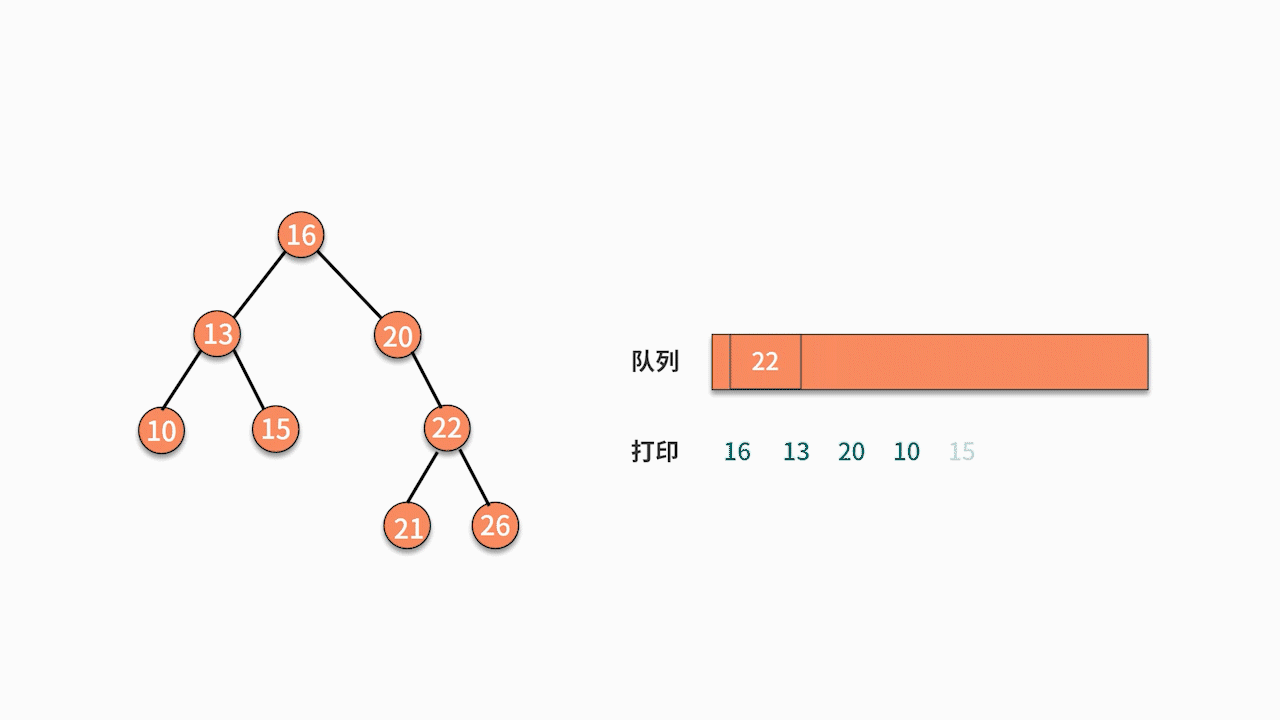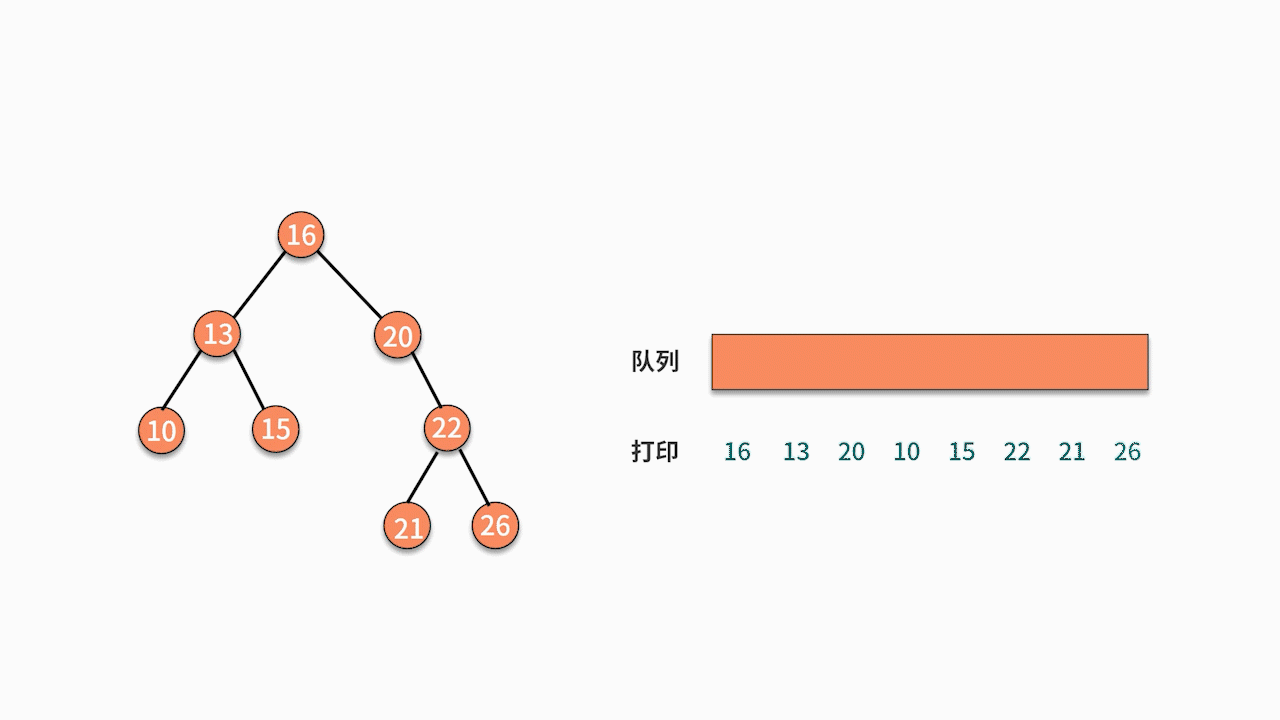
// level traversal
void levelOrderTraversal(TreeNode root) {
if(root == null) {
return;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode top = queue.poll();
System.out.print(top.val+" ");
if(top.left != null) {
queue.offer(top.left);
}
if(top.right!=null) {
queue.offer(top.right);
}
}
System.out.println();
}2. Reactor
① Concept
1. Heap logic is a complete binary tree
2. The heap is physically stored in an array
3. If the value of any node is greater than the value of the node in its subtree, it is called large heap, or large root heap, or maximum heap
4. On the contrary, it is a small heap, or a small root heap, or a minimum heap
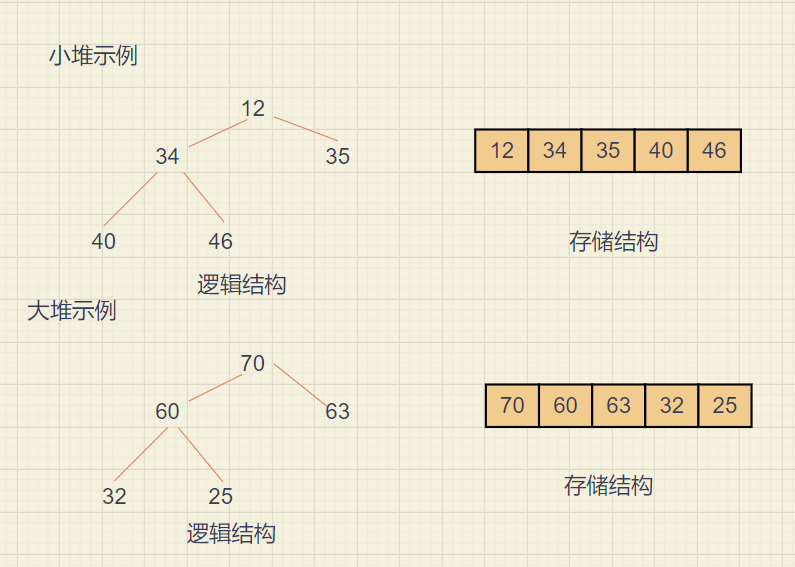
② Operation - downward adjustment
Premise:
The left and right subtrees must be a heap before they can be adjusted.
explain:
1. array represents the array of storage heap
2. size represents the number of heap data in the array
3. index represents the subscript of the position to be adjusted
4. left stands for index left subscript
5. right stands for index right subscript
6. min represents the minimum value of index and the child's subscript
Process (taking small heap as an example):
If I index is already a leaf node, the whole adjustment process ends
1. Judge whether there are children in the school
2. Because the heap is a complete binary tree, if there is no left child, there must be no right child, so judge whether there is a left child
3. Because the storage structure of the heap is an array, judge whether there is a left child, that is, judge whether the left child subscript is out of bounds, that is, left > = size is out of bounds
II determine left or right, who is the youngest child of index min
1. If the right child does not exist, min = left
2. Otherwise, compare the values of array[left] and array[right], and select the smaller value as min
Ⅲ compare the value of array[index] with the value of array[min]. If array[index] < = array[min], the nature of the heap is met and the adjustment is completed
IV. otherwise, exchange the values of array[index] and array[min]
Ⅴ then, because the nature of the heap at the Min position may be destroyed, take min as an index and repeat the above process downward
Downward adjustment takes the binary tree traversed by sequence as an example
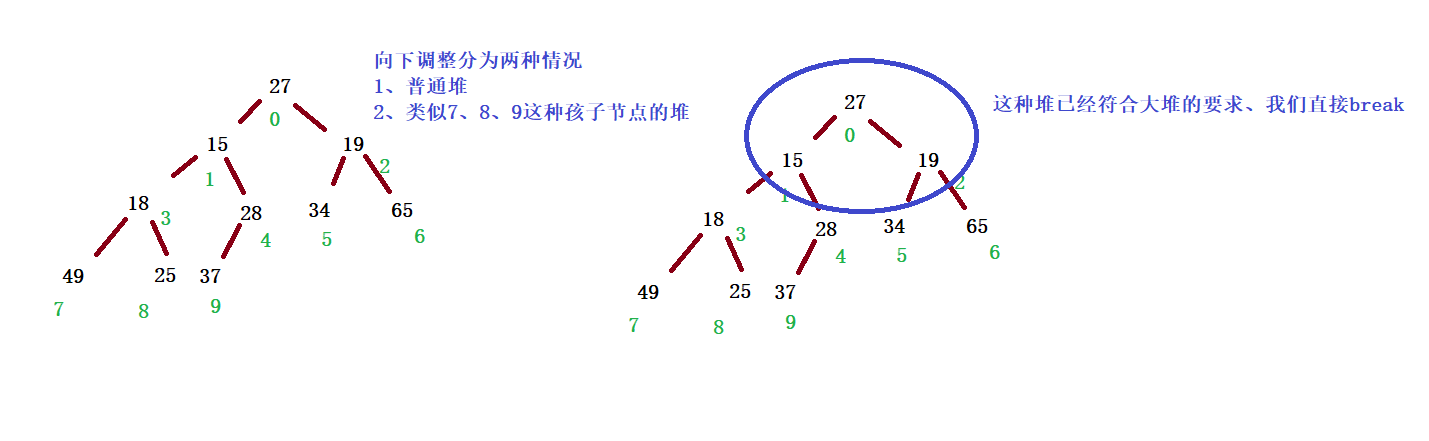
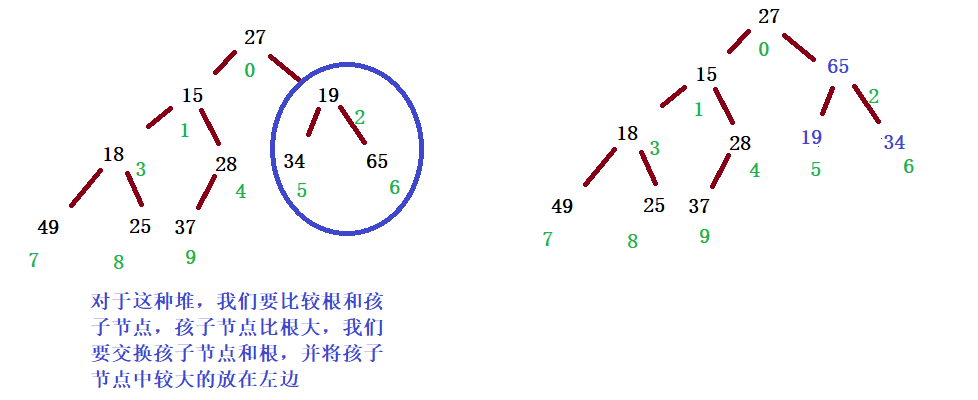
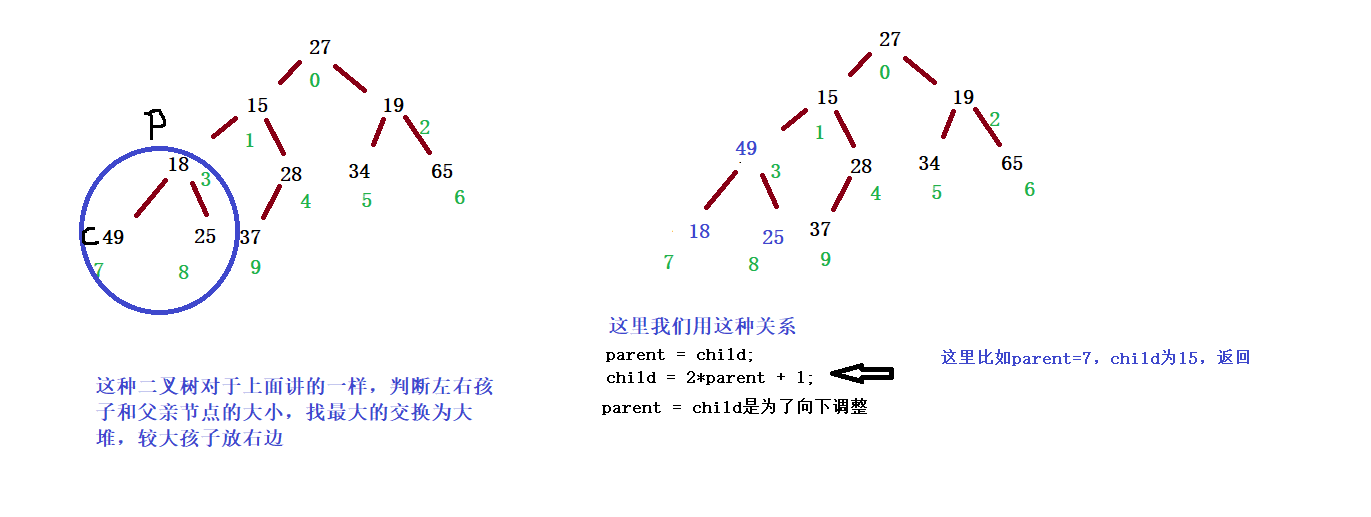
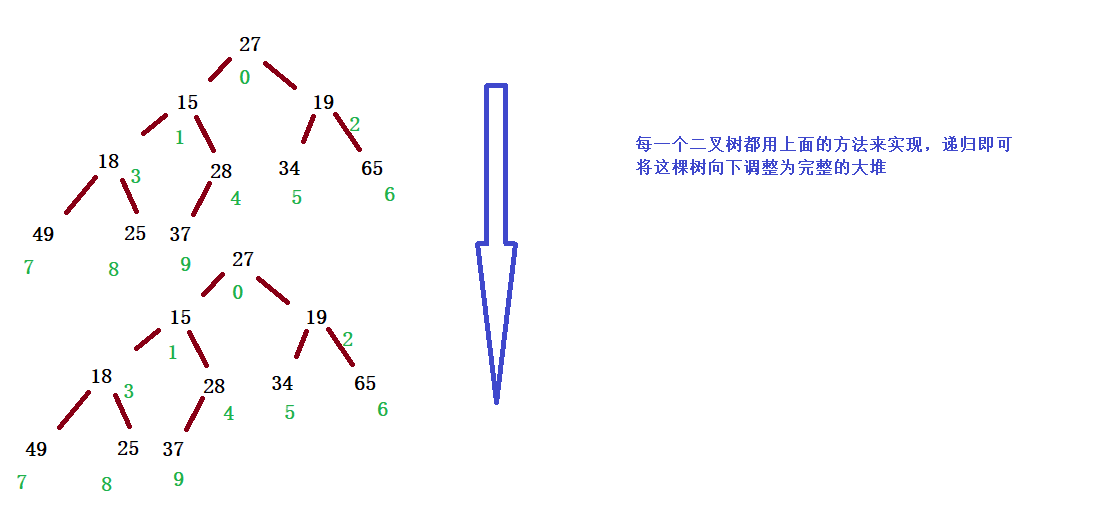
public void adjustDown(int root,int len){
int parent = root;
int child = 2*parent + 1;
while(child < len){
if (child + 1 < len && this.elem[child] < this.elem[child + 1] ){
child++;
}
if(this.elem[child] > this.elem[parent]){
int tmp = this.elem[parent];
this.elem[parent] = this.elem[child];
this.elem[child] = tmp;
parent = child;
child = 2*parent + 1;
}else{
break;
}
}
}③ Pile building (taking pile building as an example)
Next, we give an array, which can be logically regarded as a complete binary tree, but it is not a heap. Now we build it into a heap through an algorithm. The left and right subtrees of the root node are not heaps. How can we adjust them? Here, we start from the subtree of the penultimate non leaf node to the tree of the root node.
//Build a pile
public void creatHeap(int[] array){
for (int i = 0; i < array.length;i++){
this.elem[i] = array[i];
suedSize++;
}
for (int parent = (array.length - 1 - 1) / 2;parent >= 0;parent--){
adjustDown(parent,this.suedSize);
}3. Heap application - priority queue
① Concept
In many applications, we usually need to process the objects according to the priority. For example, we first process the objects with the highest priority, and then process the objects with the second highest priority. The simplest example is that when playing games on the mobile phone, if there is an incoming call, the system should give priority to the incoming call. In this case, our data structure should provide two basic operations, one is to return the highest priority object, and the other is to add a new object. This data structure is called priority queue
② Internal principle
There are many ways to implement priority queues, but the most common is to build them using heaps.
③ Queue
Process (for example):
1. First put the array in the tail insertion mode
2. Compare its value with that of its parents. If the value of its parents is large, it meets the nature of the heap and the insertion ends
3. Otherwise, exchange the value of its and parent position, and repeat steps 2, 3 and 4 Up to the root node
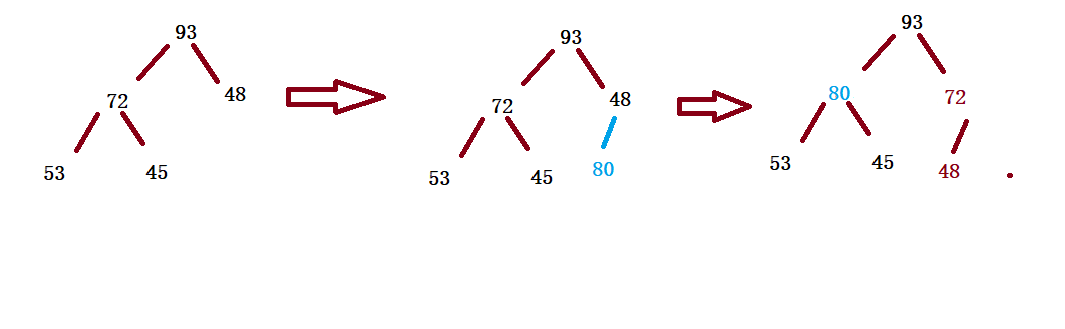
public void adjustUp(int child){
int parent = (child - 1) / 2;
while(child>0){
if(this.elem[child] > this.elem[parent]){
int tmp = this.elem[parent];
this.elem[parent] = this.elem[child];
this.elem[child] = tmp;
child = parent;
parent = (child - 1) / 2;
}else {
break;
}
}
}public void push(int val) {
if (isFull()) {
this.elem = Arrays.copyOf(this.elem, 2 * this.elem.length);
this.elem[this.suedSize] = val;
this.suedSize++;
adjustUp(this.suedSize - 1);
}
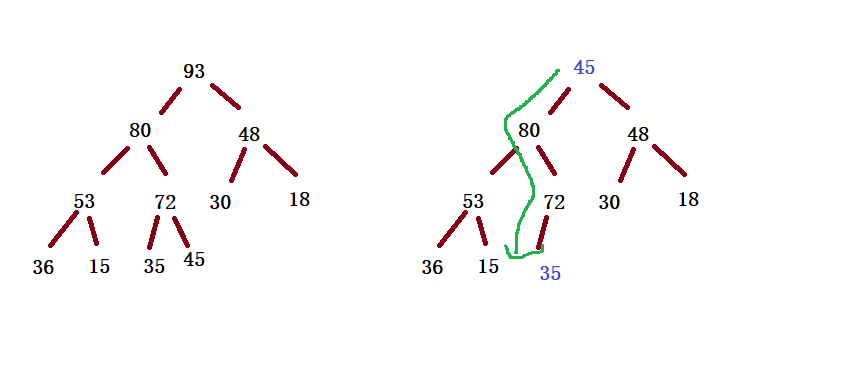
}④ Out of queue (highest priority)
In order to prevent the structure of the heap from being damaged, the top element of the heap is not deleted directly, but replaced with the last element of the array, and then readjusted into the heap by adjusting downward
public boolean isEmpty(){
return this.suedSize == 0;
} public void pop(){
if(isEmpty()){
return;
}
int tmp = this.elem[0];
this.elem[0] = this.elem[this.suedSize-1];
this.elem[this.suedSize-1] = tmp;
this.suedSize--;
adjustDown(0,this.suedSize);
}⑤ Return to the first element of the queue (highest priority)
public int peek(){
if(isEmpty()){
return -1;
}
return this.elem[0];
} public boolean isFull(){
return this.suedSize == this.elem.length;
}4. Heap sorting
/**
* You must create a lot first
* Adjust each tree
* Start heap sort:
* First exchange and then adjust until 0 subscript.
*/
public void heapSort(){
int end = this.suedSize-1;
while (end > 0){
int tmp = this.elem[0];
this.elem[0] = this.elem[end];
this.elem[end] = tmp;
adjustDown(0,end);
end--;
}
}6, Sort
1. Concept
① Sort
Sorting is the operation of arranging a string of records incrementally or decrementally according to the size of one or some keywords. In the normal context, if sorting is mentioned, it usually refers to ascending order (non descending order). In the normal sense, sorting refers to in place sort.
② Stability
If the sorting algorithm can ensure that the relative position of two equal data does not change after sorting, we call the algorithm a stable sorting algorithm
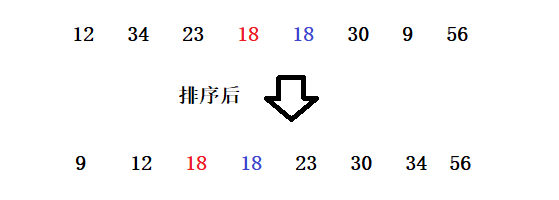
Or we say that the sort without jump is also a stable sort
2. Detailed sorting
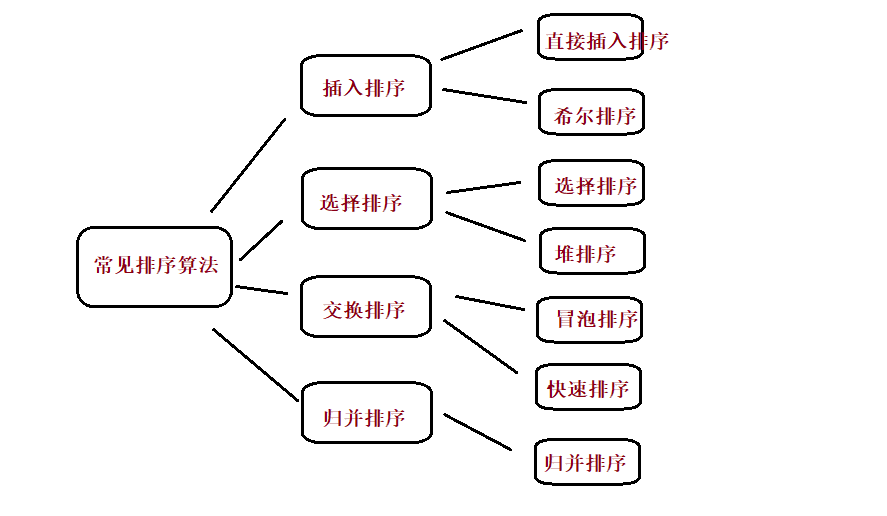
① Direct insert sort
The whole interval is divided into
1. Ordered interval
2. Disordered interval
Select the first element of the unordered interval each time and insert it at the appropriate position in the ordered interval
public static void main(String[] args) {
int[] array = {12,5,9,34,6,8,33,56,89,0,7,4,22,55,77};
insertSort(array);
System.out.println(Arrays.toString(array));
} /**
* Time complexity:
* Best: O (n) - > the data is ordered
* Worst case: O (n ^ 2) - > unordered data
* Space complexity: O(1)
* Stability: stable sorting
* @param array
*/
public static void insertSort(int[] array) {
for(int i = 1;i < array.length;i++) {//n-1
int tmp = array[i];
int j = i-1;
for(; j >= 0;j--) {//n-1
if(array[j] > tmp) {
array[j+1] = array[j];
}else{
//array[j+1] = tmp;
break;
}
}
array[j+1] = tmp;
}
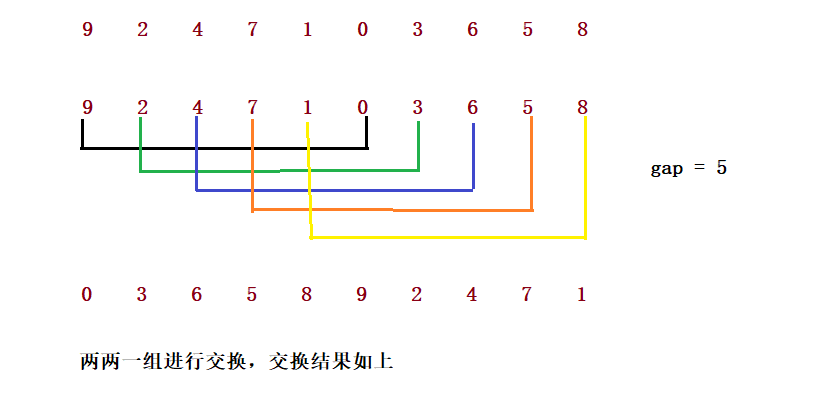
}② Hill sort
Hill ranking method is also known as reduced incremental method. The basic idea of hill sorting method is to select an integer first, divide all records in the file to be sorted into groups, divide all records with distance into the same group, and sort the records in each group. Then, take and repeat the above grouping and sorting. When arrival = 1, all records are arranged in a unified group.
1. Hill sort is the optimization of direct insertion sort.
2. When gap > 1, it is pre sorted to make the array closer to order. When gap == 1, the array is close to ordered, which will be very fast. In this way, the optimization effect can be achieved as a whole. We can compare the performance test after implementation.
/**
* Time complexity: not easy to calculate between n^1.3 - n^1.5
* Space complexity: O(1)
* Stability: unstable sorting
* Tip: if there is no jumping exchange in the process of comparison, it is stable
* @param array
*
*
* @param array Sorted array
* @param gap Interval per group - number of groups
*/
public static void shell(int[] array,int gap) {
for (int i = gap; i < array.length; i++) {
int tmp = array[i];
int j = i-gap;
for (; j >= 0; j -= gap) {
if(array[j] > tmp) {
array[j+gap] = array[j];
}else {
break;
}
}
array[j+gap] = tmp;
}
}public static void main(String[] args) {
int[] array = {12,5,9,34,6,8,33,56,89,0,7,4,22,55,77};
shell(array,5);
System.out.println(Arrays.toString(array));
}
③ Direct selection sort
Each time, the largest (or smallest) element is selected from the unordered interval and stored at the end (or front) of the unordered interval until all data elements to be sorted are arranged.
public static void main(String[] args) {
int[] array = {12,5,9,34,6,8,33,56,89,0,7,4,22,55,77};
selectSort(array);
System.out.println(Arrays.toString(array));
} /**
* Time complexity:
* Best: O(N^2)
* Worst case: O(N^2)
* Space complexity: O(1)
* Stability: unstable
* @param array
*/
public static void selectSort(int[] array) {
for (int i = 0; i < array.length; i++) {
for (int j = i+1; j < array.length; j++) {
if(array[j] < array[i]) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
}
}
}
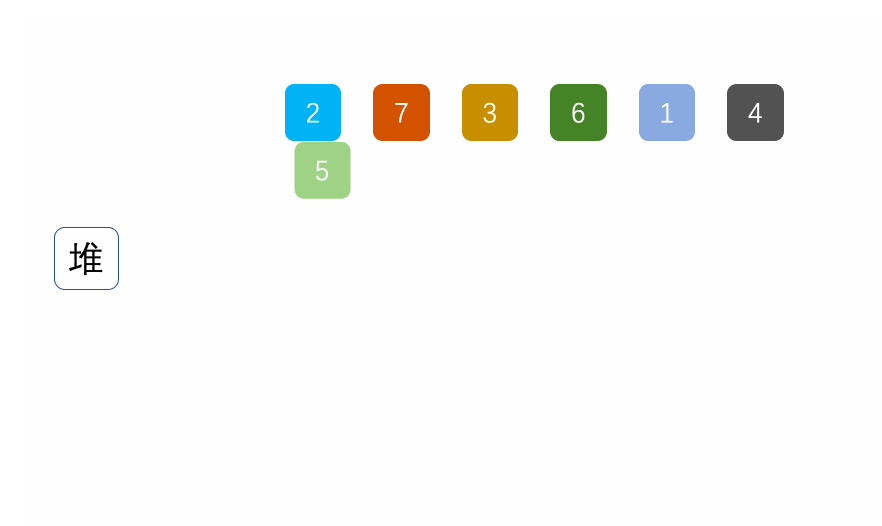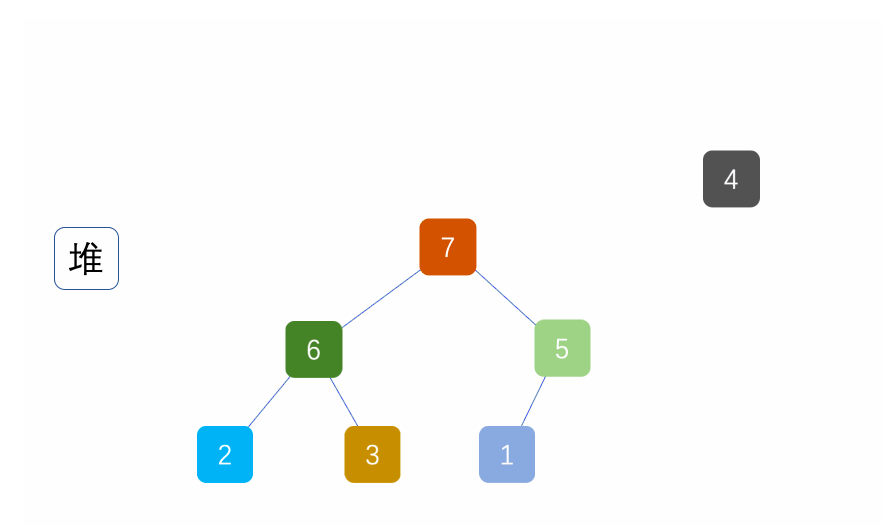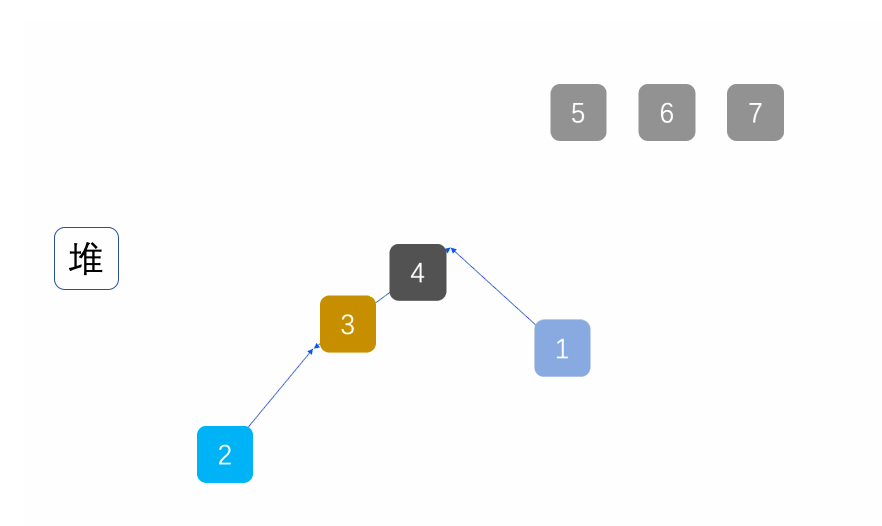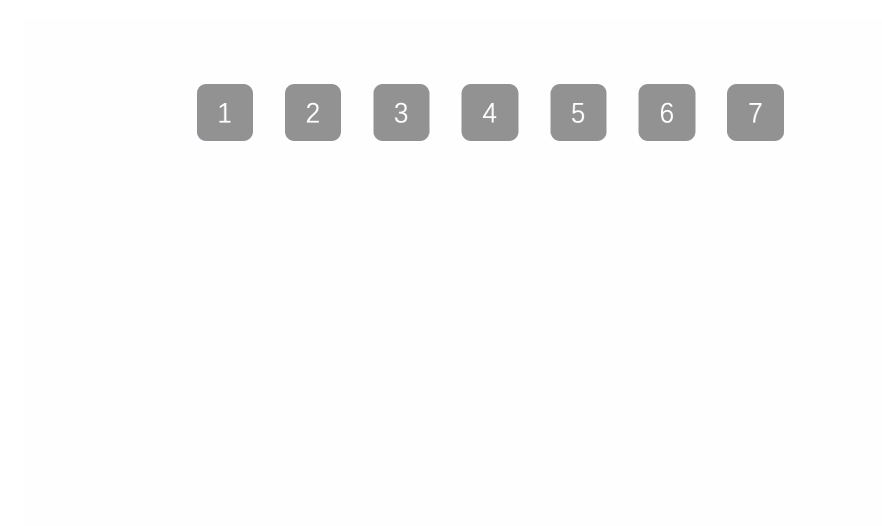
④ Heap sort
The basic principle is also selective sorting, but instead of using traversal to find the maximum number of unordered intervals, it selects the maximum number of unordered intervals through the heap.
Note: a lot should be built in ascending order; In descending order, small piles should be built.
public static void main(String[] args) {
int[] array = {12,5,9,34,6,8,33,56,89,0,7,4,22,55,77};
heapSort(array);
System.out.println(Arrays.toString(array));
} public static void siftDown(int[] array,int root,int len) {
int parent = root;
int child = 2*parent+1;
while (child < len) {
if(child+1 < len && array[child] < array[child+1]) {
child++;
}
//The child subscript is the maximum subscript of the left and right children
if(array[child] > array[parent]) {
int tmp = array[child];
array[child] = array[parent];
array[parent] = tmp;
parent = child;
child = 2*parent+1;
}else {
break;
}
}
}
public static void createHeap(int[] array) {
//Sort from small to large - large root heap
for (int i = (array.length-1 - 1) / 2; i >= 0 ; i--) {
siftDown(array,i,array.length);
}
}
/**
* Time complexity: O(N*logN) is the time complexity
* Complexity: O(1)
* Stability: unstable sorting
* @param array
*/
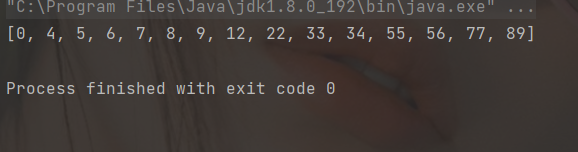
public static void heapSort(int[] array) {
createHeap(array);//O(n)
int end = array.length-1;
while (end > 0) {//O(N*logN)
int tmp = array[end];
array[end] = array[0];
array[0] = tmp;
siftDown(array,0,end);
end--;
}
}
⑤ Bubble sorting
In the unordered interval, through the comparison of adjacent numbers, bubble the largest number to the end of the unordered interval, and continue this process until the array is ordered as a whole
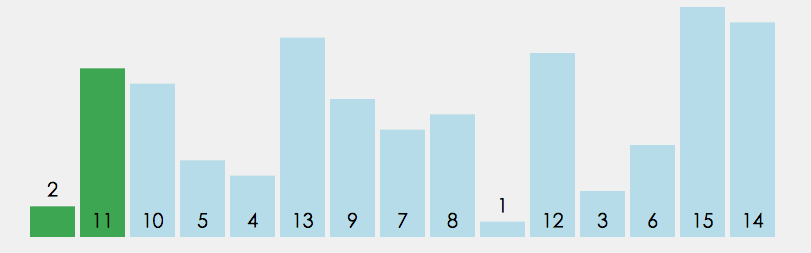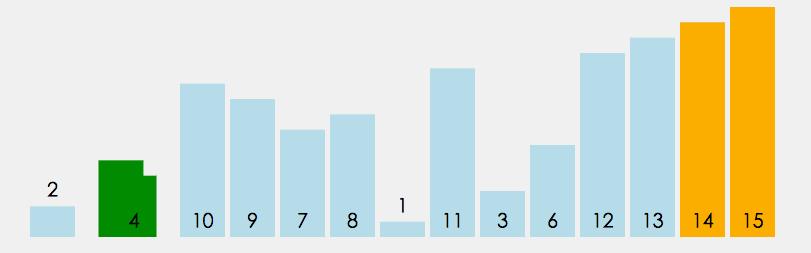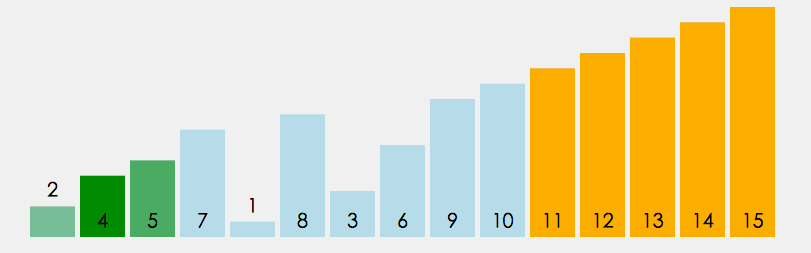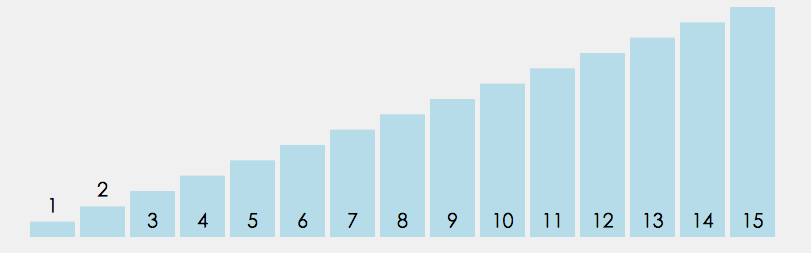
public static void main(String[] args) {
int[] array = {12,5,9,34,6,8,33,56,89,0,7,4,22,55,77};
bubbleSort(array);
System.out.println(Arrays.toString(array));
} /**
* Time complexity:
* The best and worst are O(n^2)
* Space complexity: O(1)
* Stability: stable sorting
* Bubbling direct insertion
* @param array
*/
public static void bubbleSort(int[] array) {
for (int i = 0; i < array.length-1; i++) {
for (int j = 0; j < array.length-1-i; j++) {
if(array[j] > array[j+1]) {
int tmp = array[j];
array[j] = array[j+1];
array[j+1] = tmp;
}
}
}
}
⑥ Quick sort
1. Select a number from the interval to be sorted as the benchmark value (pivot);
2. Partition: traverse the entire range to be sorted, put the smaller (can contain equal) than the benchmark value to the left of the benchmark value, and put the larger (can contain equal) than the benchmark value to the right of the benchmark value;
3. Using the divide and conquer idea, the left and right cells are processed in the same way until the length between cells = = 1, which means that they are in order, or the length between cells = = 0, which means that there is no data
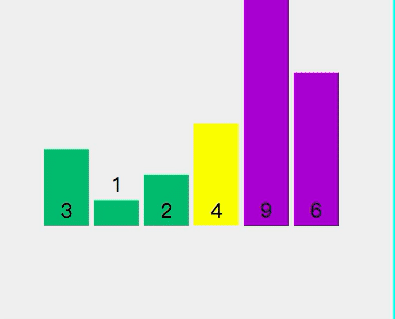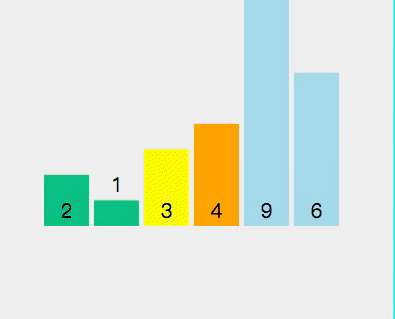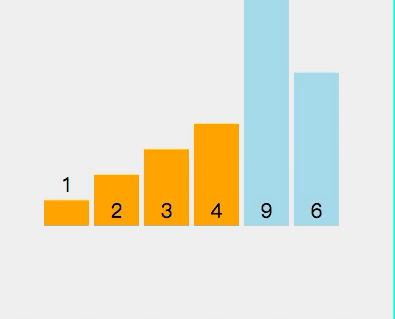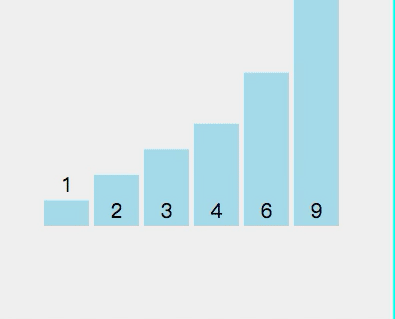
public static void main(String[] args) {
int[] array = {12,5,9,34,6,8,33,56,89,0,7,4,22,55,77};
quickSort1(array);
System.out.println(Arrays.toString(array));
}public static int partition(int[] array,int low,int high) {
int tmp = array[low];
while (low < high) {
while (low < high && array[high] >= tmp) {
high--;
}
array[low] = array[high];
while (low < high && array[low] <= tmp) {
low++;
}
array[high] = array[low];
}
array[low] = tmp;
return low;
}
public static void quick(int[] array,int start,int end) {
if(start >= end) {
return;
}
int mid = (start+end)/2;
int pivot = partition(array,start,end);
quick(array,start,pivot-1);
quick(array,pivot+1,end);
}
/**
* Time complexity:
* Best: O(n*logn) under uniform segmentation
* Worst: o(n^2) when the data is in order
* Space complexity:
* Best: logn
* Worst case: O(n)
* Stability: unstable sorting
*
* k*n*logn
* 2
* 1.2
* @param array
*/
public static void quickSort1(int[] array) {
quick(array,0,array.length-1);
}
⑦ Merge sort
Merge sort is an effective sort algorithm based on merge operation. The algorithm adopts Divide and Conquer method A very typical application of (Divide and Conquer). Merge the ordered subsequences to obtain a completely ordered sequence; that is, order each subsequence first, and then order the subsequence segments. If two ordered tables are merged into one ordered table, it is called two-way merging.
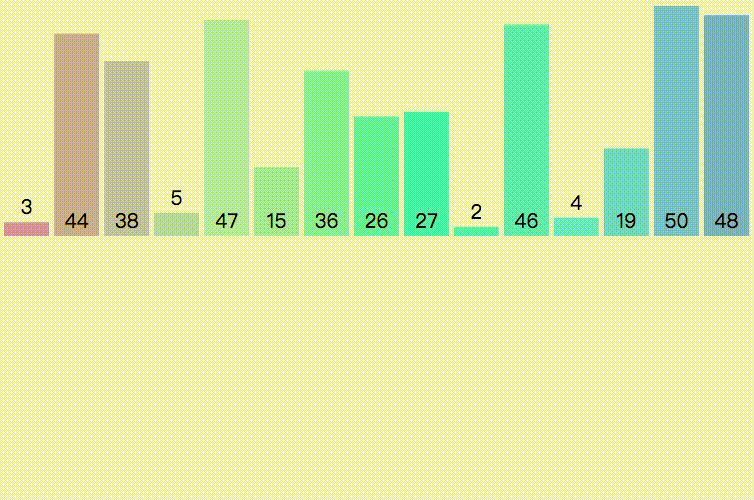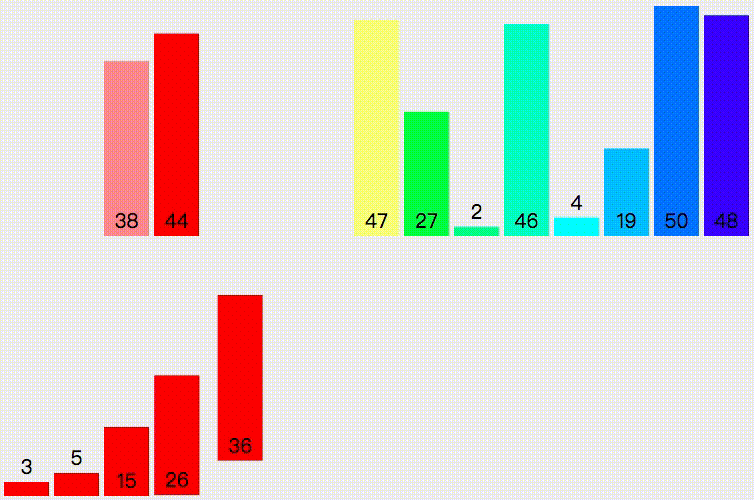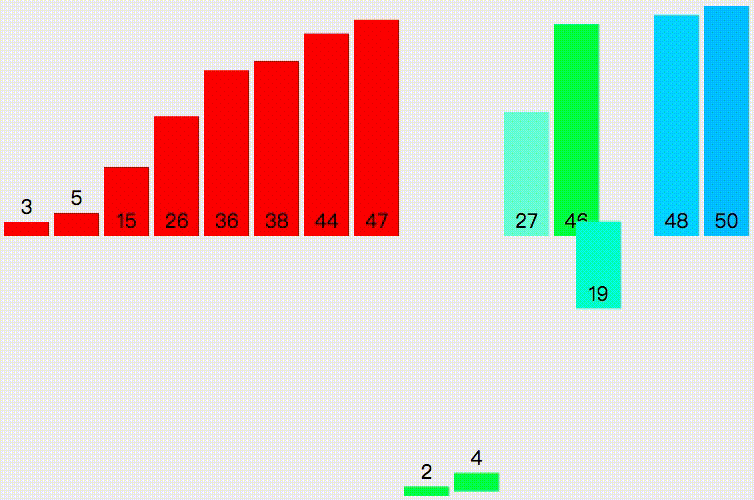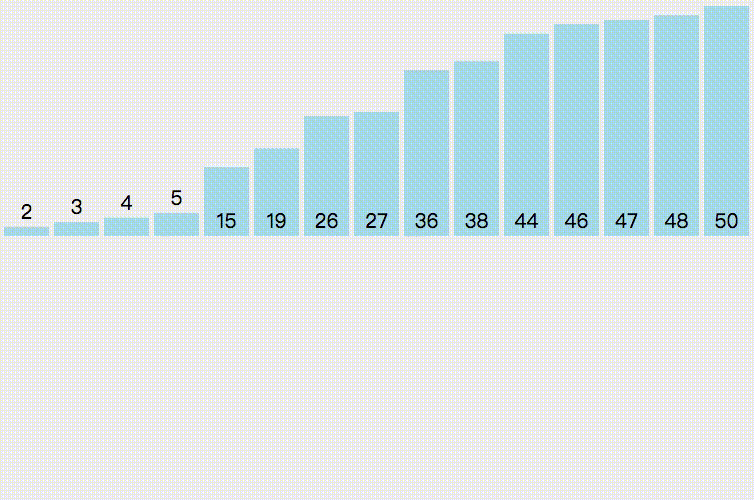
public static void main(String[] args) {
int[] array = {12,5,9,34,6,8,33,56,89,0,7,4,22,55,77};
mergeSort1(array);
System.out.println(Arrays.toString(array));
}public static void merge(int[] array,int low,int mid,int high) {
int s1 = low;
int e1 = mid;
int s2 = mid+1;
int e2 = high;
int[] tmp = new int[high-low+1];
int k = 0;//Represents the subscript of the tmp array
while (s1 <= e1 && s2 <= e2) {
if(array[s1] <= array[s2]) {
tmp[k++] = array[s1++];
}else {
tmp[k++] = array[s2++];
}
}
//There are two situations
while (s1 <= e1){
//It indicates that there is no data in the second merging segment, and copy all the remaining data in the first merging segment
tmp[k++] = array[s1++];
}
while (s2 <= e2) {
//It indicates that there is no data in the first merging segment, and copy all the remaining data in the second merging segment
tmp[k++] = array[s2++];
}
//The tmp array stores the currently merged data
for (int i = 0; i < tmp.length; i++) {
array[i+low] = tmp[i];
}
}
public static void mergeSortInternal(int[] array,int low,int high) {
if(low >= high) {
return;
}
int mid = (low+high) / 2;
mergeSortInternal(array,low,mid);
mergeSortInternal(array,mid+1,high);
//Merging process
merge(array,low,mid,high);
}
/**
* Time complexity: O(N*log n)
* Space complexity: O(N)
* Stability: stable
* @param array
*/
public static void mergeSort1(int[] array) {
mergeSortInternal(array, 0,array.length-1);
}
7, List
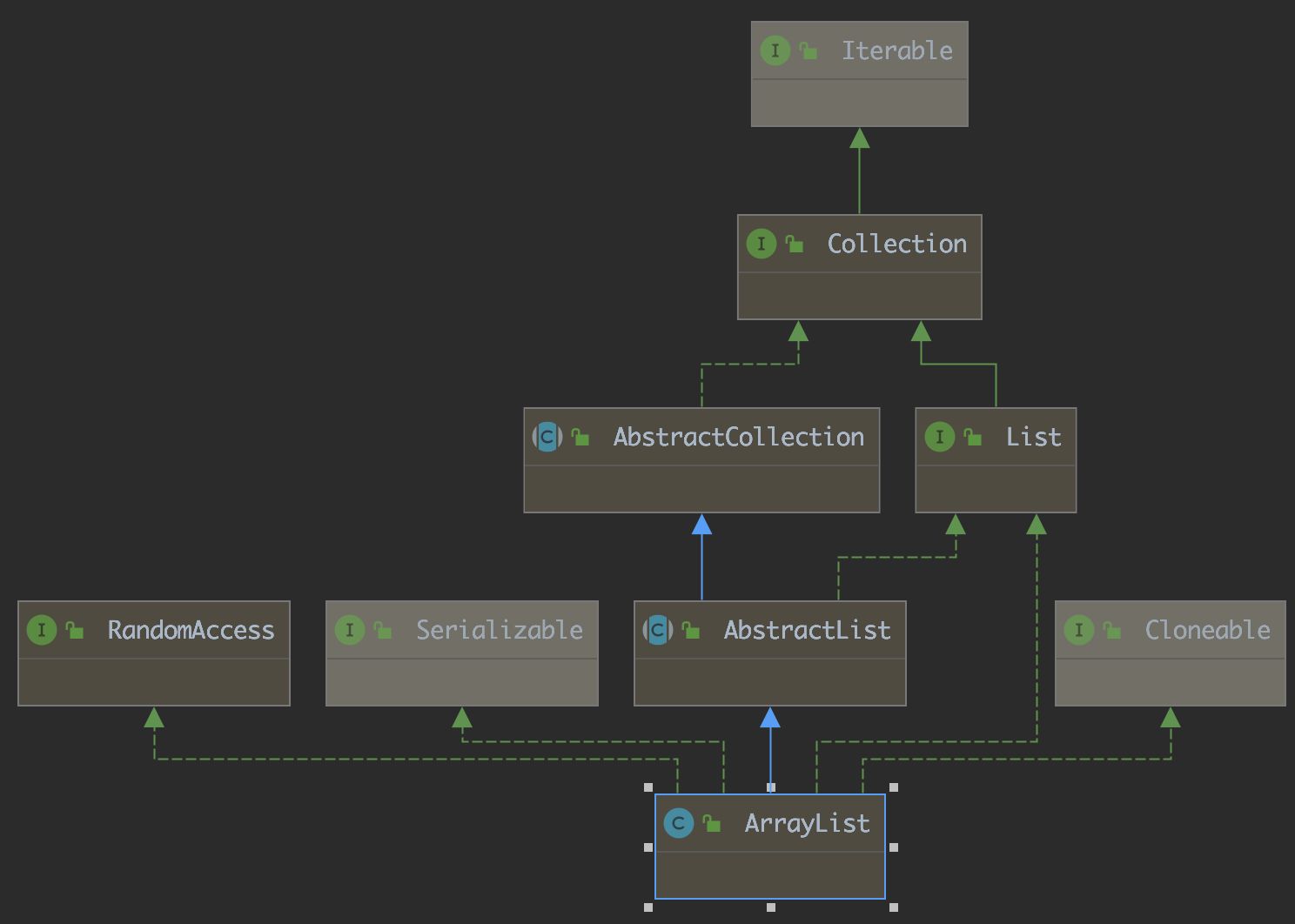
1. Introduction to ArrayList
[description]
1. ArrayList implements the RandomAccess interface, indicating that ArrayList supports random access
2. ArrayList implements Cloneable interface, which indicates that ArrayList can clone
3. ArrayList implements the Serializable interface, indicating that ArrayList supports serialization
4. Unlike vector, ArrayList is not thread safe and can be used in a single thread. Vector or CopyOnWriteArrayList can be selected in multiple threads
5. The bottom layer of ArrayList is a continuous space and can be dynamically expanded. It is a dynamic type sequence table
2. Use ArrayList
① Construction of ArrayList
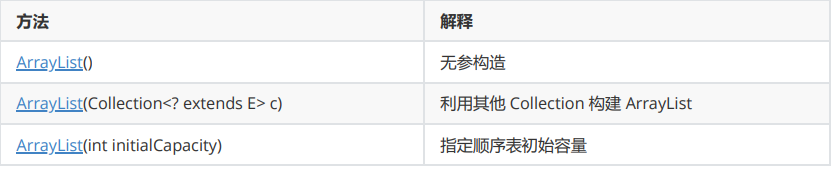
public static void main(String[] args) {
// It is recommended to create ArrayList
// Construct an empty list
List<Integer> list1 = new ArrayList<>();
// Construct a list with 10 capacities
List<Integer> list2 = new ArrayList<>(10);
list2.add(1);
list2.add(2);
list2.add(3);
// list2.add("hello"); // Compilation failed. List < integer > has been defined. Only integer elements can be stored in List2
// After list3 is constructed, it is consistent with the elements in the list
ArrayList<Integer> list3 = new ArrayList<>(list2);
// Avoid omitting types, otherwise: elements of any type can be stored, and it will be a disaster when used
List list4 = new ArrayList();
list4.add("111");
list4.add(100);
}② ArrayList common operations
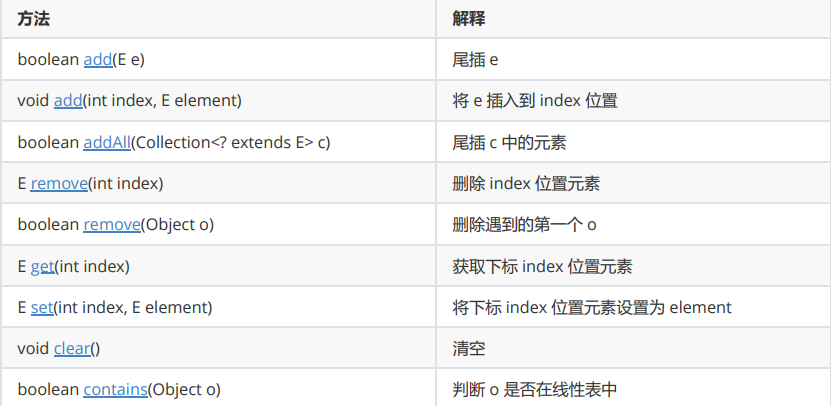
public static void main(String[] args) {
ArrayList<String> list = new ArrayList<>();
list.add("1234");
list.add("zhongguo");
list.add("aaaaa");
list.add("gao");
System.out.println(list);
}
//add source code
public boolean add(E e) {
ensureCapacityInternal(size + 1); // Increments modCount!!
elementData[size++] = e;
return true;
} public static void main(String[] args) {
ArrayList<String> list = new ArrayList<>();
list.add("1234");
list.add("zhongguo");
list.add("aaaaa");
list.add("gao");
list.add(2,"ssss");
System.out.println(list);
}
//add insert source code
public void add(int index, E element) {
rangeCheckForAdd(index);
ensureCapacityInternal(size + 1); // Increments modCount!!
System.arraycopy(elementData, index, elementData, index + 1,
size - index);
elementData[index] = element;
size++;
} public static void main(String[] args) {
ArrayList<String> list = new ArrayList<>();
list.add("1234");
list.add("zhongguo");
list.add("aaaaa");
list.add("gao");
ArrayList<String> list2 = new ArrayList<>();
list2.add("111");
list2.add("44554");
list.addAll(list2);
System.out.println(list);
}
//addAll source code
public boolean addAll(Collection<? extends E> c) {
Object[] a = c.toArray();
int numNew = a.length;
ensureCapacityInternal(size + numNew); // Increments modCount
System.arraycopy(a, 0, elementData, size, numNew);
size += numNew;
return numNew != 0;
}
public static void main(String[] args) {
ArrayList<String> list = new ArrayList<>();
list.add("1234");
list.add("zhongguo");
list.add("aaaaa");
list.add("gao");
list.remove(2);
System.out.println(list);
}
public static void main(String[] args) {
ArrayList<String> list = new ArrayList<>();
list.add("1234");
list.add("zhongguo");
list.add("aaaaa");
list.add("gao");
String a = list.get(1);
System.out.println(a);
System.out.println(list);
}
③ Traversal of ArrayList
public static void main(String[] args) {
ArrayList<String> list = new ArrayList<>();
list.add("hello");
list.add("123");
list.add("jsss");
System.out.println(list);
System.out.println("===================");
for (int i = 0; i < list.size(); i++) {
System.out.print(list.get(i) + " ");
}
System.out.println();
System.out.println("=====================");
for (String s : list) {
System.out.print(s + " ");
}
System.out.println();
System.out.println("=========Iterator printing=======");
Iterator<String> it = list.iterator();
while (it.hasNext()){
System.out.print(it.next() + " ");
}
System.out.println();
System.out.println("==========iterator list Print=======");
ListIterator<String> it2 = list.listIterator();
while (it2.hasNext()){
System.out.print(it2.next() + " ");
}
}
8, Map and Set
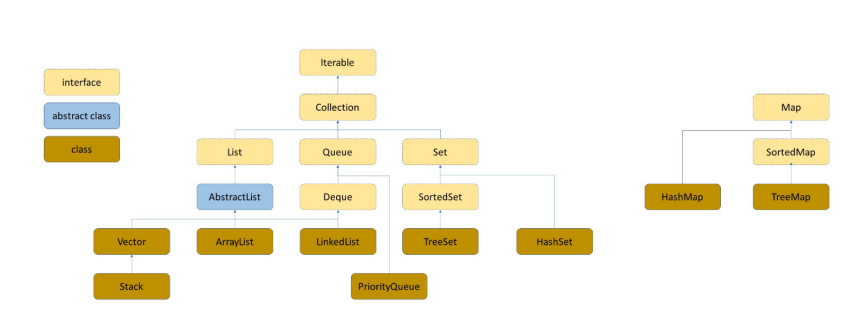
1. Search
① Concept and scenario
Map and set are special containers or data structures for searching, and their search efficiency is related to their specific instantiation subclasses.
Search methods are:
1. Direct traversal. The time complexity is O(N). If there are many elements, the efficiency will be very slow
2. Binary search has a time complexity of, but the sequence must be ordered before the search. The above sorting is more suitable for static search, that is, the interval is generally not inserted or deleted, but in reality, such as:
1. Query test scores by name
2. Address book, i.e. inquire the contact information according to the name
3. Do not duplicate the set, that is, you need to search whether the keyword is already in the set
② Model
Generally, the searched data is called Key, and the corresponding Key is called Value, which is called Key Value pair. Therefore, there are two models:
1. Pure key model, such as:
There is an English dictionary to quickly find out whether a word is in the dictionary or not
2. Key value model, for example:
Count the number of times each word appears in the file. The statistical result is that each word has its corresponding number of times: Liangshan hero's Jianghu nickname: each hero has his own Jianghu nickname
2. Use of Map
① Description of Map
Map is an interface class, which does not inherit from Collection. The key value pairs of the structure are stored in this class, and K must be unique and cannot be repeated.
② About map Description of entry
Map.Entry is an internal class implemented in map and used to store the mapping relationship between Key value pairs. This internal class mainly provides the acquisition of values, the setting of values and the comparison method of keys.
| method | explain |
| K getKey() | Returns the value of the key in the entry |
| V getValue() | Return value in entry |
| V setValue(V value) | Replace the value in the key value pair with the specified value |
③ Description of common methods of Map
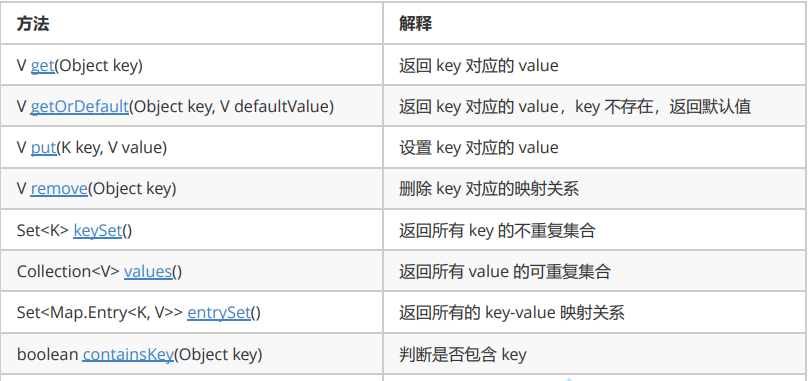
public static void main(String[] args) {
Map<String,String> map = new HashMap<>();
map.put("123","Li Bai");
map.put("124","Du Fu");
map.put("125","wang changling");
map.put("126", "known as a model of fidelity to the last Song sovereigns");
System.out.println(map);
}
public static void main(String[] args) {
Map<String,String> map = new HashMap<>();
map.put("123","Li Bai");
map.put("124","Du Fu");
map.put("125","wang changling");
map.put("126", "known as a model of fidelity to the last Song sovereigns");
String val = map.get("123");
System.out.println(val);
} public static void main(String[] args) {
Map<String,String> map = new HashMap<>();
map.put("123","Li Bai");
map.put("124","Du Fu");
map.put("125","wang changling");
map.put("126", "known as a model of fidelity to the last Song sovereigns");
String val;
val = map.getOrDefault("123","Li Bai");
System.out.println(val);
}
3. Use of Set
① Description of common methods
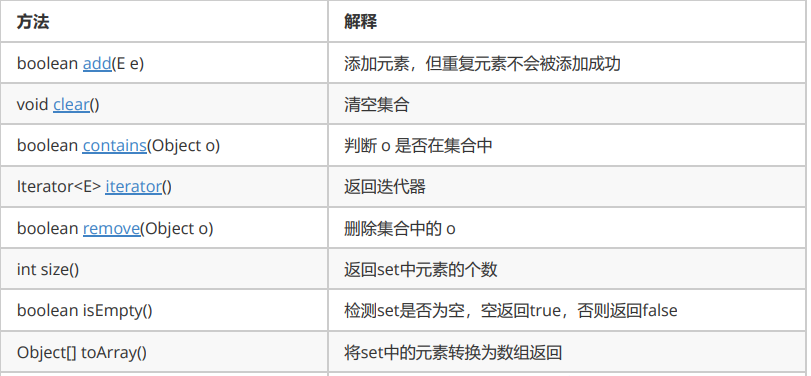
② Use case of TreeSet
public static void main(String[] args) {
Set<String> set = new HashSet<>();
set.add("123");
set.add("124");
set.add("125");
System.out.println(set);
}
public static void main(String[] args) {
Set<String> set = new HashSet<>();
set.add("123");
set.add("124");
set.add("125");
boolean fla = set.contains("123");
System.out.println(fla);
}
public static void main(String[] args) {
Set<String> set = new HashSet<>();
set.add("123");
set.add("124");
set.add("125");
Iterator<String> it = set.iterator();
while (it.hasNext()){
System.out.println(it.next());
}
}
