As long as you keep reading it, I'm sure you can learn it!!
Preface
Definition of Dynamic Planning (DP): Dynamic Planning is an extension of the idea of division, and in a general sense, it is the art of turning big things into small ones and small things into nothing.
Dynamic planning has the following three characteristics:
- The original problem is broken down into several similar subproblems.
- All sub-problems need to be solved only once.
- Storing solutions to subproblems
And we usually start from the following four perspectives (important)
- State Definition
- Definition of transfer equation between states
- Initialization of state
- Return results
1. Why use dynamic planning?
Let's start with a topic like this
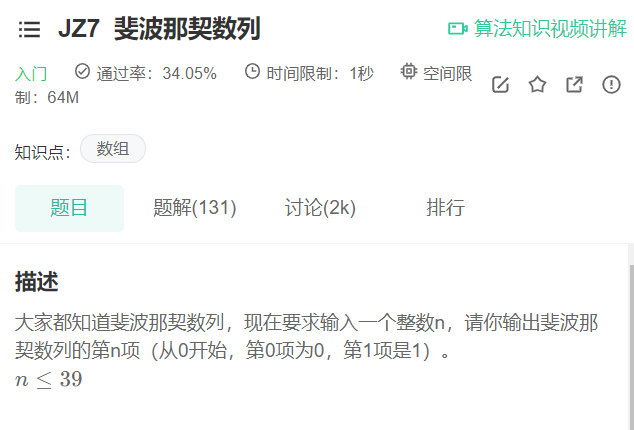
Fibonacci
Click on the link to jump: Fibonacci series
Classmates may learn C initially and recursion is a classic topic. We usually do it in a recursive way, but we find that when we recursively implement the Fibonacci number algorithm with 2^n time complexity, the number will not be calculated when it is large, so we will use the idea of dynamic planning.
Say nothing more. Now let's see how we can use our four steps to complete the subject, following the logic we gave above.
Definition of state: finding the value of F(n)
Transition of equation of state: F(n)=F(n-1)+F(n-2)
Initialization: F(0)=0; F(1)=1
Return result: F(n)
C++Realization:
class Solution {
public:
int Fibonacci(int n) {
vector<int> v;
//Initialization
v.push_back(0);
v.push_back(1);
//Transfer equation of state
for(int i=2;i<=n;i++)
{
int ret = v[i - 1] + v[i - 2];
v.push_back(ret);
}
//Return results
return v[n];
}
};
2. Maximum Continuous Subarrays and
Maximum Continuous Subarray and

int FindGreatestSumOfSubArray(vector<int> array)
Here we should think about how his state is defined. Assuming we use the maximum sum of the arrays of the first i elements as the definition of state here, we will find that we cannot use the previous state to make changes to the next state.
Here we define the state: the largest subarray ending with the first element
Reason: When we add new elements, we can add them and keep them in a continuous subarray, depending on whether they need to be added or not
State recursion: F[i] = max(F[i-1]+array[i-1],array[i-1]); This means that if the last maximum value is added to the current value, it will be placed in F(i) much larger than the element itself.
Result: The largest value returned to our array is the largest subarray and
class Solution {
public:
int FindGreatestSumOfSubArray(vector<int> array) {
int sz = array.size();
vector<int> F(sz+1);
//Initialization
F[1] = array[0];
for(int i =2;i<=sz;i++)
{
//Recursive equation: maximum sum of subarrays ending in i
F[i] = max(F[i-1]+array[i-1],array[i-1]);
}
int maxI = F[1];
for(int i =2 ;i<= sz;++i)
{
maxI = max(F[i],maxI);
}
return maxI;
}
};
3. LC12 Split Words and Sentences
bool wordBreak(string s, unordered_set<string> &dict)
Analytical Title: This is to determine whether a string can be split into values found in dictionary dicts within a given string
Status Definition: Can the first i characters be found in dict
**State Transition:**Let's start by explaining that the state transition is not necessarily an equation. For example, here, it is defined as j<i && F(j) && (j+1, i) being a word in dict. To explain this, we are going to use the state of the first J characters, the current j characters are found in dict. That is, F(j) is true, and we only need to be able to ensure that the whole is true if the interval in judgment (j+1, i) is also a string that can be found in dict! (It doesn't matter if F(j) here is composed of two or more characters, if it can be found in dict, it means he is true)
Initialization: We can give an empty string as the starting state here. On this basis, the state transition equation indicates that the string as a whole can be found in dict, that is, F[0] is set to true.
class Solution {
public:
bool wordBreak(string s, unordered_set<string> &dict) {
// The first j characters can be found in dict
// Equation of state: j<i && f[j] && [j+1, i] constituent characters
// Special case: first character
// F[0] ture, F[1] -- To make F[0] ancillary, so that the first j characters as a whole can be found in dict
int n = s.size();
vector<bool> canBreak(n+1 ,false);//First i Characters--Map Subscript Position
canBreak[0]=true;//This is a secondary state
for(int i= 1; i <= n;i++)//Processing first to nth characters
{
for(int j =i-1 ; j >= 0 ;j--)
{
if(canBreak[j] && dict.find(s.substr(j,i-j))!=dict.end())// Equation of state: j<i && f[j] && [j+1, i] constituent characters
{
canBreak[i] =true;
}
}
}
return canBreak[n];
}
};
The state transition of this question is actually not as good as the previous two questions, but when we think about it, we can think that the problem of state transition has actually been solved, so most of the time it is just a step away.
4. Triangles
Jump Link: Triangle
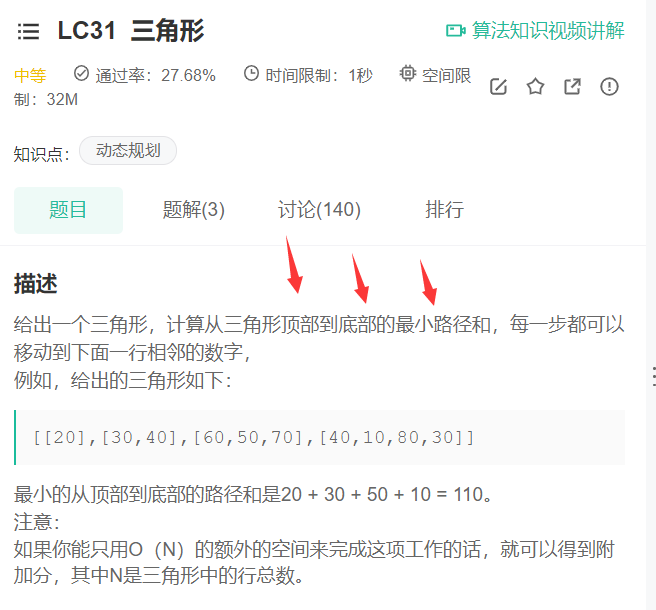
int minimumTotal(vector<vector<int> > &triangle)
It's easy to tell the result like the one given by the title, but what if we change line 70 to line 1?
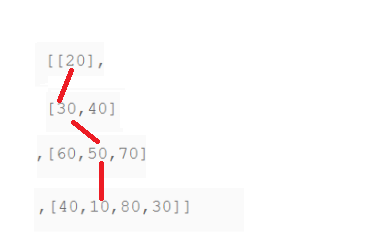
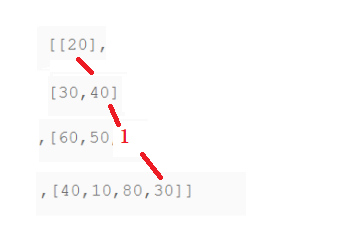
Example illustrated in the following figure: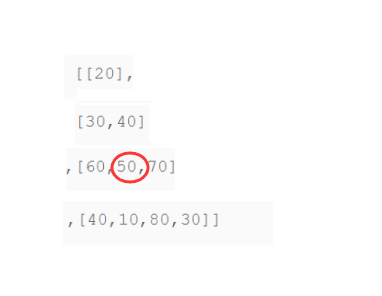
Examples of initialization:
Analysis: Looking at the two tables in the figure above, we can see that the minimum sum from top to bottom is required, and a single move can only move from (i,j) - > (i+1, j), (i+1, j+1). It is obvious that we cannot directly select the minimum value for the next row, so we need a two-dimensional array to save all the subarrays and F(i,j)
Status Definition: Minimum to Line i
State transition: Analyse as 50 in the figure: because the size of the current row is F(i, j) -->
Min (F (i-1, j), F (i-1, j-1)+ (i, j), that is, we can save the minimum sum of everything that comes down from above, for example: 50 This position is from 20 --> 30 --> 50, so the two-dimensional array corresponding to 50 stores this 100--which should be understood.
Initialization: As you can see from the diagram above, when j== 0, i.e. the first column and when i==j, diagonals may only come from fixed positions, so when we initialize, we set these values to their corresponding values first
Solution: My solution uses updates directly in the two-dimensional array triangle they give us, because we can just update the values back when we walk through the array
class Solution {
public:
int minimumTotal(vector<vector<int> > &triangle) {
// Record the minimum value of the current position directly with a triangle two-dimensional array
// Initializing column 0 should add the value of the previous row plus the value of this row. i==j adds the current value to the previous (i-1,j-1) value, and the other locations are the minimum value of the previous row and the column on the previous row plus the current value
int x =triangle.size();
for(int i =1;i<x;i++)
{
for(int j=0;j<i+1;j++)
{
if(j==0)
triangle[i][j]=triangle[i-1][j]+triangle[i][j];
else if(i == j)
{
triangle[i][j]=triangle[i-1][j-1]+triangle[i][j];
}
else
{
triangle[i][j]=triangle[i][j]+min(triangle[i-1][j-1],triangle[i-1][j]);
}
}
}
int y =triangle[x-1].size();
int minret= triangle[x-1][0];
for(int i=1;i<y;++i)
{
minret = min(minret,triangle[x-1][i]);
}
return minret;
}
};
5. LC88 Find Path
Interpretation: The meaning of this question is very simple. The path is from the beginning to the end, and it can only go down or to the right at a time.
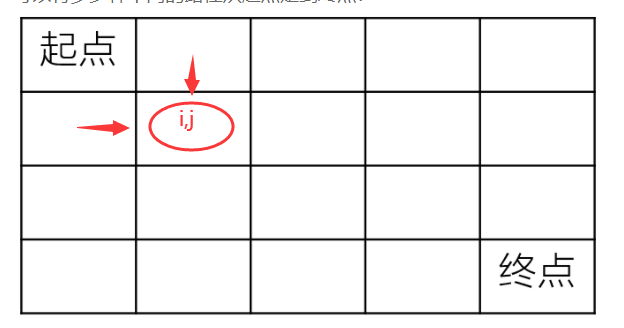
According to the figure above: Each point path actually adds the path from the previous row and the left column to that location, so we use a two-dimensional array to save the results of the sub-answers
Status Definition: Number of paths from (0,0) to (i,j)
State transition: F(i,j) =F(i-1,j)+F(i,j-1) - that is, the sum of the path and number of each point on the previous row and the column on the left
Initialization: Observe that the first row and the first column have only one possibility, going all the way to the right and down, so we set them all to 1 at initialization;
Return: F (m-1, n-1)
class Solution {
public:
/**
*
* @param m int integer
* @param n int integer
* @return int integer
*/
int uniquePaths(int m, int n) {
// write code here
//State transition -- (i,j) is obtained by taking (i-1,j) one step more than (i,j-1)
vector<vector<int>> retArr(m,vector<int>(n,0));
retArr[0][0]=1;
for(int i =1;i<m;++i)
{
retArr[i][0]=1;//Processing first column
}
for(int i =1;i<n;++i)
{
retArr[0][i]=1;//Processing first line
}
for(int i = 1;i<m;++i)
{
for(int j =1;j<n;++j)
{
retArr[i][j] =retArr[i-1][j]+retArr[i][j-1];
}
}
return retArr[m-1][n-1];
}
};
6. LC87 Finding Path ii
Analysis: Compared to the previous question where barriers were added, where we set paths and zeros, we conclude that each point path is the sum of the paths from the previous row and the left column to that location, so we use a two-dimensional array to save the results of the sub-answers as well here
Status Definition: Number of paths from (0,0) to (i,j)
State transition: F(i,j) =F(i-1,j)+F(i,j-1) - that is, the sum of the path and number of each point on the previous row and the column on the left
Initialization: Initialize We will place the first row, the first column with a barrier at the back of 0, and (0,0) return directly to 0 if there is a barrier or a barrier at the end
Tip: We can set our two-dimensional arrays to 0 in advance, so that when we initialize traversal, we break out of the loop, which is equivalent to completing the subsequent initialization, see the code below!!!
class Solution {
public:
/**
*
* @param obstacleGrid int Integer vector<vector< >>
* @return int integer
*/
int uniquePathsWithObstacles(vector<vector<int> >& obstacleGrid) {
// write code here
// To (i,j)!= 1 when
// Equals (i-1,j) and (i,j-1)
// 0,0 returns directly to 1 at initialization
// After initialization we set all the barriers to zero, so that we can apply the above ideas
if(obstacleGrid.empty())
return 0;
int x =obstacleGrid.size();
int y =obstacleGrid[0].size();
if(obstacleGrid[0][0]||obstacleGrid[x-1][y-1])
return 0;
vector<vector<int>> retArr(x,vector<int>(y,0));//Set to 0 for easy follow-up
for(int i=0;i<x;i++)
{
if(obstacleGrid[i][0] == 1)
break;//If there are any obstacles, we'll just quit
retArr[i][0]=1;
}
for(int i=0;i<y;i++)
{
if(obstacleGrid[0][i] == 1)
break;
retArr[0][i]=1;
}
for(int i =1;i<x;i++)
{
for(int j =1;j<y;j++)
{
if(obstacleGrid[i][j]==0)
retArr[i][j] = retArr[i-1][j]+retArr[i][j-1];
else
retArr[i][j]= 0;
}
}
return retArr[x-1][y-1];
}
};
Similar topics: LC86 Minimum Weighted Path Sum And try it yourself
7. Backpack problems

If, by the time you see this, you are already able to deduce by yourself the state definition and transformation equation for this question and listen to me again, it may be easier to absorb.
Status:
F(i, j): The maximum value of the first iItem in a backpack of size J. If J is not set as a variable, the maximum value of the first iItem in a backpack will not be able to determine if the current backpack size is large enough for the current item - difficult
Status Recursion: There is an exception to item i I that cannot be loaded, two choices, put or hold
If it doesn't fit: the value at this point is the same as that of the first i-1
F(i,j) = F(i-1,j), if loadable: need to find the largest of two choices
F(i, j) =max(F[i-1][j-A[i-1]]+V[i-1],F[i-1][j])
F(i-1,j): Indicates that the second item is not put in the backpack, so its value is the maximum value of the first I-1 item in a backpack of size J
F(i-1, j-A[i]) + V[i]: Indicates that the value of item I I is added to the value of the item in the backpack, but the size of item j-A[i] needs to be made available for item I I
We analyzed the situation by topic
Initialization: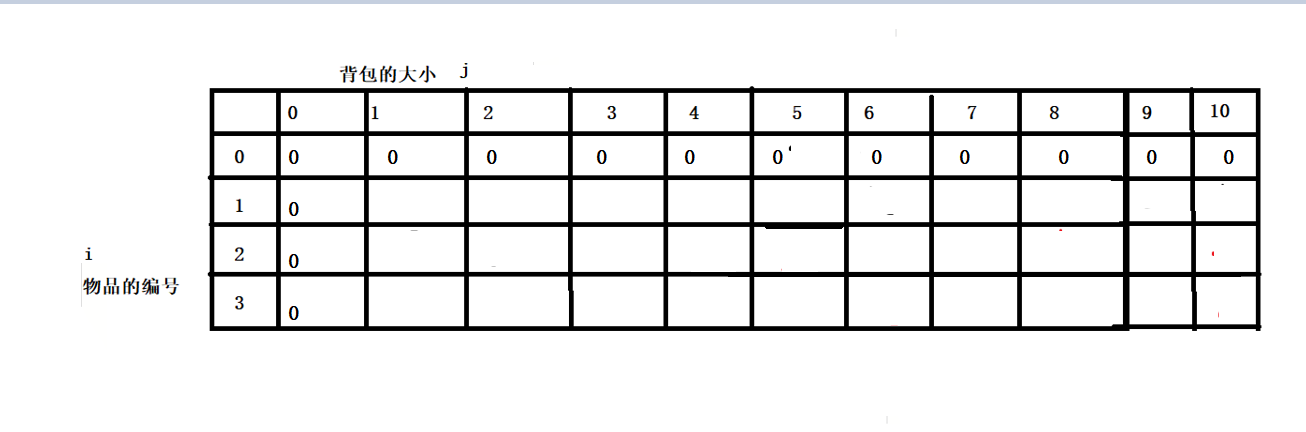
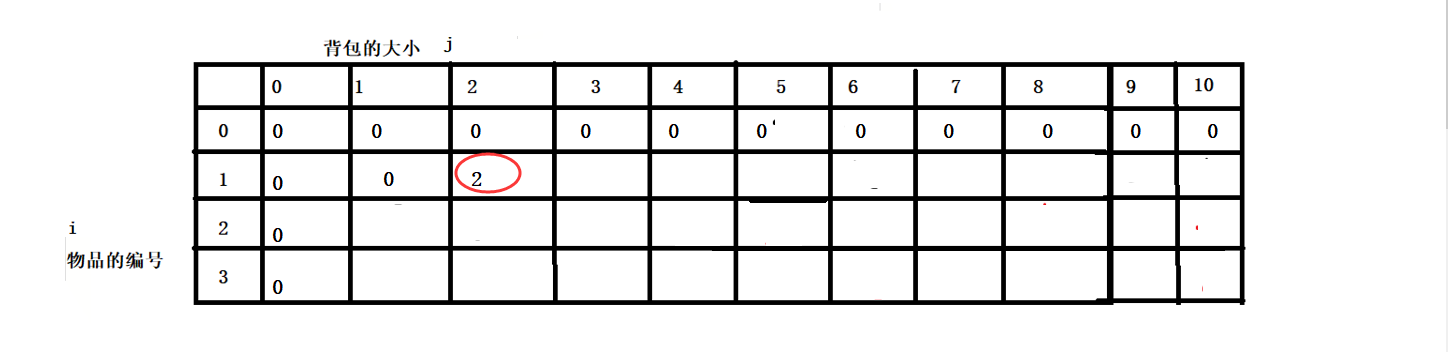
This is a separate analysis of the two points, followed by a similar one. When we consider whether to put 2 or not, we need to consider the remaining capacity j-A[i-1], which is 0, so we add the value when the size of the previous row of backpacks is 0, which is the current maximum.
max(vv[i-1][j-A[i-1]]+V[i-1],vv[i-1][j])
Here's another example
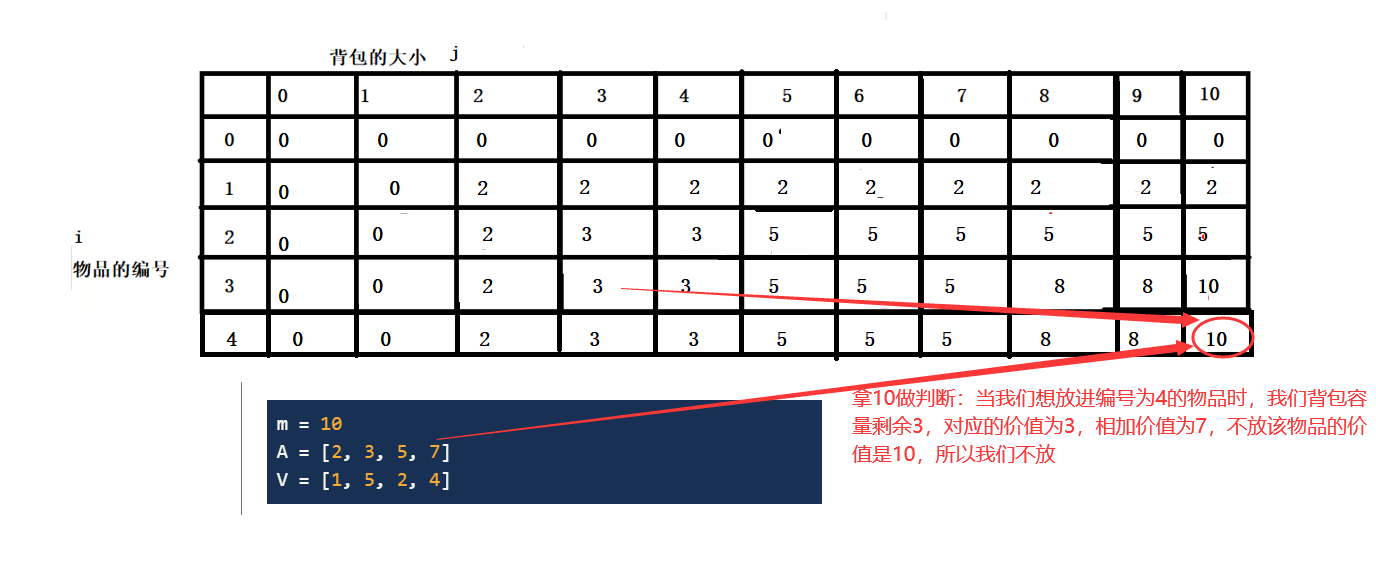
summary
Dynamic planning should do more on its own, all of which have to be done. Next time we talk about it, you will have ideas if you do more. Palindrome string splitting, editing problems and different subsequences, this section of knowledge if you do not understand the welcome to discuss with me, it is not easy to make, one click three links!!