Why write study notes again
Pre knowledge: weight segment tree.
First, it is very simple to use the weighted line segment tree to find the Kth of the set. Equivalent to a binary operation.
The problem to be considered now is interval static Kth, that is, given a sequence \ (a \), ask the smaller number of \ (k \) in an interval \ ([l,r] \) many times.
Or consider the dichotomy on the weight line segment tree. Set the current node as \ (p \), and count the number of numbers \ (x \) falling in the interval represented by the left son of \ (p \) in \ ([l,r] \). If \ (x\ge k \), then prove that the answer must be in the left half interval. Go directly to the left. Otherwise, subtract \ (x \) from \ (k \) and go to the right.
The problem is how to quickly find the number of numbers falling in the interval represented by a node.
Consider building \ (n \) segment trees. For each \ (i \) from \ (1 \) to \ (n \), a weight segment tree is built separately to store the results of inserting each \ (a \) in \ ([1,i] \) into the segment tree. At the same time, for each segment tree, define \ (cnt_p \) to represent the number of nodes falling in the interval represented by \ (P \). In this way, when finding the above thing, you only need to subtract \ (CNT \) on the segment tree \ (r \) from the segment tree \ (l-1 \).
But there is still a problem: space will explode.
Further analysis shows that the segment tree \ (I \) only inserts one more number than the segment tree \ (i-1 \), and only \ (\ log SIZE \) nodes (\ (SIZE \) represents the value range) are changed at most. Therefore, you only need to create \ (\ log \) nodes.
Here is a picture from oi wiki.
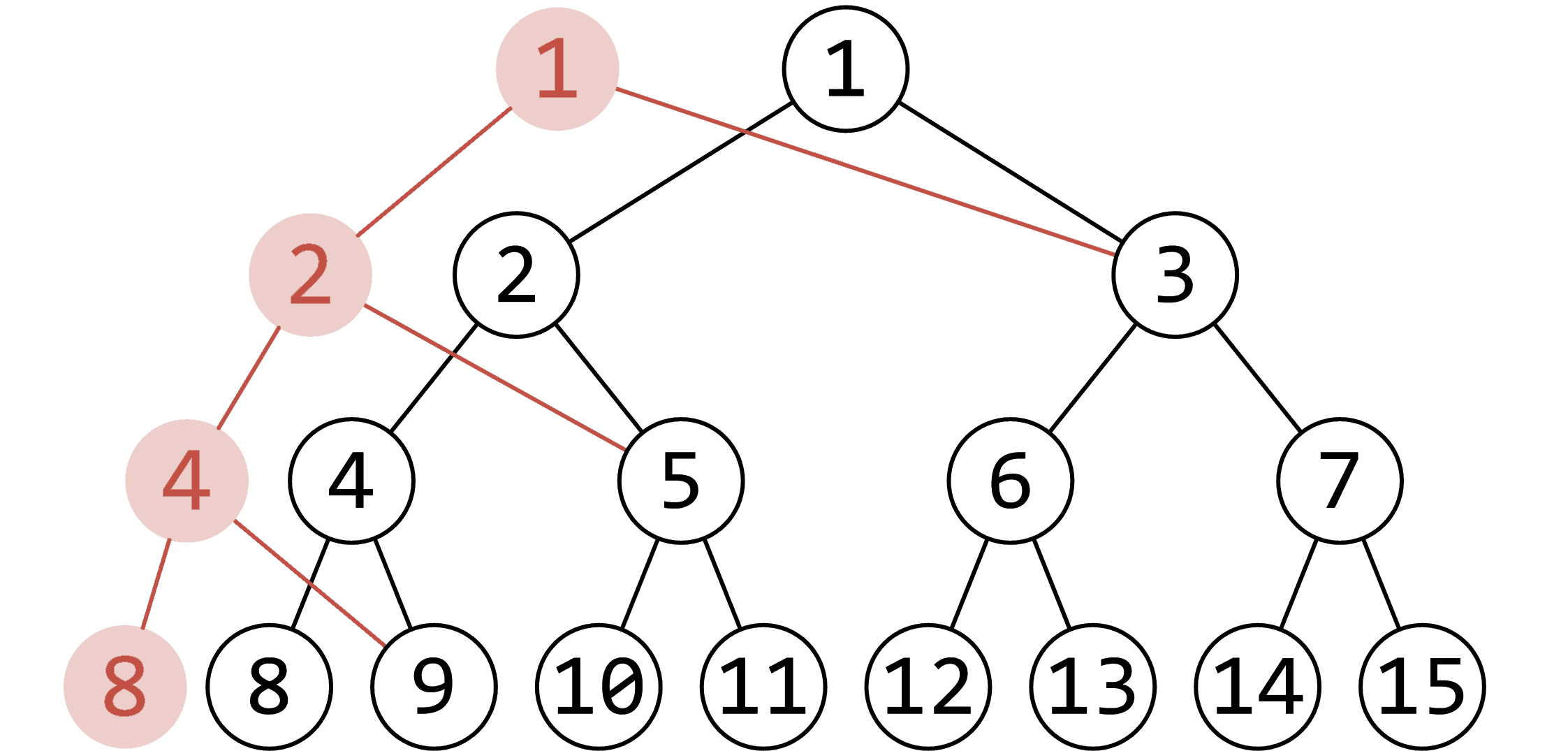
Red indicates the new node.
In this way, each insert operation can create up to \ (\ log \) nodes, and the space complexity is \ (O(n\log n) \).
Time complexity \ (O(n\log n) \).
#include<bits/stdc++.h>
using namespace std;
const int maxn = 2e5 + 5;
int n, m, len;
int a[maxn], ind[maxn], rt[maxn];
struct PresidentTree {
#define mid (l + r >> 1)
int ls[maxn << 5], rs[maxn << 5], sum[maxn << 5];
int cnt;
int build(int l, int r) {
int k = ++cnt;
if (l == r) return k;
ls[k] = build(l, mid); rs[k] = build(mid + 1, r);
return k;
}
int update(int k, int l, int r, int val) {
int dir = ++cnt; ls[dir] = ls[k]; rs[dir] = rs[k]; sum[dir] = sum[k] + 1;
if (l == r) return dir;
if (val <= mid) ls[dir] = update(ls[k], l, mid, val);
else rs[dir] = update(rs[k], mid + 1, r, val);
return dir;
}
int query(int l, int r, int p, int q, int val) {
if (l == r) return l;
int x = sum[ls[q]] - sum[ls[p]];
if (val <= x) return query(l, mid, ls[p], ls[q], val);
else return query(mid + 1, r, rs[p], rs[q], val - x);
}
} t;
void discrete() {
memcpy(ind, a, sizeof(a));
sort(ind + 1, ind + 1 + n);
len = unique(ind + 1, ind + 1 + n) - ind - 1;
for (int i = 1; i <= n; i++)
a[i] = lower_bound(ind + 1, ind + 1 + len, a[i]) - ind;
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++)
cin >> a[i];
discrete();
t.build(1, len);
for (int i = 1; i <= n; i++)
rt[i] = t.update(rt[i - 1], 1, len, a[i]);
for (int i = 1; i <= m; i++) {
int l, r, k; cin >> l >> r >> k;
cout << ind[t.query(1, len, rt[l - 1], rt[r], k)] << endl;
}
return 0;
}
This thing is the chairman tree. A wonderful data structure.
Several exercises:
period.