preface
★ this is Xiao Leng's blog ‡ see the column for high-quality technical articles The official account of the individual, sharing some technical articles, and the pit encountered. Current series: data structure series Source code git warehouse‘ Data structure code address Code Git warehouse address
Stack
Let's take a scene into our study
Please enter an expression
Calculation formula: [722-5 + 1-5 + 3-3] Click calculation to calculate the result
Excuse me: how does the bottom layer of the computer calculate the result? Note that it is not a simple operation to list the formula, because we look at the formula 7 * 2 * 2 - 5, but how the computer understands the formula (for the computer, what it receives is a string), we are discussing this problem. - --- > Stack
Introduction to stack
- Stack (stack)
- A stack is an ordered list of Filo first in last out.
- Stack is a special linear table that restricts the insertion and deletion of elements in a linear table to the same end of the linear table. The end that allows insertion and deletion is the changing end, which is called the top of the stack, and the other end is the fixed end, which is called the bottom of the stack.
- According to the definition of stack, the first element put in the stack is at the bottom of the stack, the last element put in is at the top of the stack, while the deleted element is just the opposite. The last element put in is deleted first, and the first element is deleted last
- The concepts of pop and push are illustrated graphically
Stack in and stack out: the characteristics of stack data structure are first in and then out


Application scenario of stack
- Subroutine call: before jumping to the subroutine, the address of the next instruction will be stored in the stack until the subroutine is executed, and then the address will be taken out to return to the original program.
- Handling recursive calls: similar to subroutine calls, except that in addition to storing the address of the next instruction, parameters, area variables and other data are also stored in the stack.
- Expression conversion [infix expression to suffix expression] and evaluation (actual solution).
- Traversal of binary tree.
- The depth first search method of graphics.
Stack quick start (array simulation stack)
Realization idea
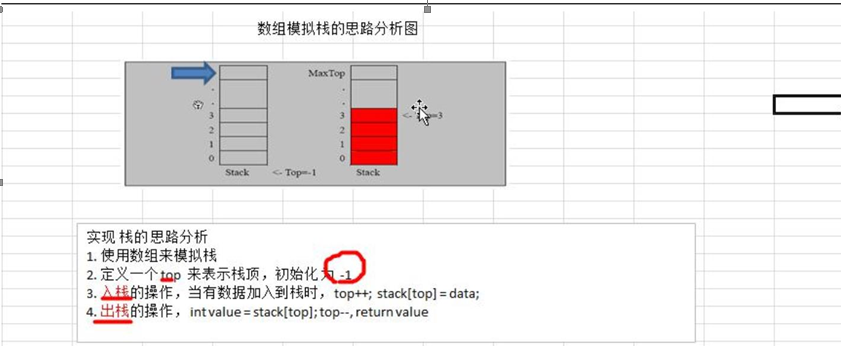
The detailed idea of each part is in the comments of the code. If you want to understand it in detail, you can refer to the comments in the code
package com.hyc.DataStructure.Stack;
import java.util.Scanner;
/**
* @projectName: DataStructure
* @package: com.hyc.DataStructure.Stack
* @className: ArrayStackDemo
* @author: Cold Huanyuan doorwatcher
* @description: TODO Use arrays to simulate stacks
* @date: 2021/12/23 18:08
* @version: 1.0
*/
public class ArrayStackDemo {
public static void main(String[] args) {
//Test whether ArrayStack is correct
//First create an ArrayStack object - > representation stack
ArrayStack stack = new ArrayStack(4);
String key = "";
boolean loop = true; //Controls whether to exit the menu
Scanner scanner = new Scanner(System.in);
while (loop) {
System.out.println("show: Indicates the display stack");
System.out.println("exit: Exit program");
System.out.println("push: Indicates adding data to the stack(Push )");
System.out.println("pop: Indicates fetching data from the stack(Out of stack)");
System.out.println("Please enter your choice");
key = scanner.next();
switch (key) {
case "show":
stack.list();
break;
case "push":
System.out.println("Please enter a number");
int value = scanner.nextInt();
stack.push(value);
break;
case "pop":
try {
int res = stack.pop();
System.out.printf("The data out of the stack is %d\n", res);
} catch (Exception e) {
System.out.println(e.getMessage());
}
break;
case "exit":
scanner.close();
loop = false;
break;
default:
break;
}
}
System.out.println("Program exit~~~");
}
}
class ArrayStack {
//Maximum stack length
private int MaxSize;
//The simulation stack data is placed in this array
private int[] stack;
// Equal to the top of the stack. By default, equal to - 1 represents the bottom part
private int top = -1;
public ArrayStack() {
}
// Initialization stack
public ArrayStack(int maxSize) {
MaxSize = maxSize;
stack = new int[maxSize];
}
//Returning to the top of the stack only shows that pop does not change the structure of the stack
public int peek() {
return stack[top];
}
//Determine whether the stack is full
public boolean isFull() {
return top == MaxSize - 1;
}
//Determine whether the stack is empty
public boolean isempty() {
return top == -1;
}
//Push data onto stack
public void push(int data) {
if (isFull()) {
System.out.println("Stack full");
return;
}
top++;
stack[top] = data;
}
// Take data out of stack
public int pop() {
if (isempty()) {
throw new RuntimeException("The stack is empty and cannot be taken out");
}
int value = stack[top];
top--;
return value;
}
//When traversing the stack, you need to display data from the top of the stack
public void list() {
if (isempty()) {
System.out.println("The stack is empty");
}
// The output from the top of the stack is actually the output array in reverse order
for (int i = top; i >= 0; i--) {
System.out.printf("stack[%d]=%d\n", i, stack[i]);
}
}
}Small summary
- Here, we use arrays to simulate some basic operations of the stack, enter the stack, exit the stack, and traverse the contents,
- In addition to using arrays, we can also use linked lists to implement stacks. I have also written this method with detailed comments. The code is as follows
package com.hyc.DataStructure.Stack;
/**
* @projectName: DataStructure
* @package: com.hyc.DataStructure.Stack
* @className: ListStackDemo
* @author: Cold Huanyuan doorwatcher
* @description: TODO Use linked list to simulate stack
* @date: 2021/12/23 18:23
* @version: 1.0
*/
public class ListStackDemo {
public static void main(String[] args) {
listStack listStack = new listStack();
listStack.push(5);
listStack.push(6);
listStack.push(9);
System.out.println("Before leaving the stack");
listStack.list();
System.out.println("After stack");
System.out.println("Out of stack:" + listStack.pop());
System.out.println("Out of stack:" + listStack.pop());
listStack.list();
}
}
class listStack {
//Create a header node
StackNode head = new StackNode(0);
StackNode temp = head;
//Judge whether it is empty
public boolean isempty() {
return head.next == null;
}
//Push into stack
public void push(int value) {
//Create node object
StackNode newnode = new StackNode(value);
//Change the direction of the header node pointer
temp.next = newnode;
//Pointer backward
temp = temp.next;
}
//Out of stack
public int pop() {
if (isempty()) {
throw new RuntimeException("Stack empty");
}
StackNode Before = head;
//Traverse the before node to temp, that is, the previous node of the last node, and let the temp pointer traverse before
while (true) {
if (Before.next == temp) {
break;
}
Before = Before.next;
}
//Making the next node of before empty is equivalent to deleting the reference after it is out of the stack
Before.next = null;
//Value
int value = temp.data;
//At this time, the node pointed to by before is the position of the previous node. Move the temp before and repeat the operation to get out of the stack
temp = Before;
return value;
}
//Traversal stack
public void list() {
// Judge non empty
if (isempty()) {
System.out.println("The stack is empty");
return;
}
StackNode temp = head;
while (true) {
if (temp.next == null) {
break;
}
System.out.println(temp.next.data);
temp = temp.next;
}
}
}
//Unidirectional linked list node
class StackNode {
// data
public int data;
//Next node
public StackNode next;
public StackNode(int data) {
this.data = data;
}
//Convenient output statement output
@Override
public String toString() {
return "StackNode{" +
", data='" + data + '\'' +
", next=" + next +
'}';
}
}Infix expression calculator
Using stack to implement comprehensive calculator

How does the computer bottom layer deal with this formula? The idea is as follows

We need to use two stacks, a record number and a record symbol. According to the data characteristics of this stack, we can calculate the formula through the occurrence rules of symbols and data
thinking
- 1. Traverse our expression through an index value (prime index)
- 2. If we find that it is a number, we will directly enter the number stack
- 3. If it is found that a symbol is scanned, it can be divided into the following situations:
- 3.1 if the current symbol stack is found to be empty, it will be directly put into the stack
- 3.2 if there are operators in the symbol stack, compare them. If the priority of the current operator is less than or equal to that in the stack
- The operator needs to pop two numbers from the number stack and pop a symbol from the symbol stack for operation,
- The result will be put into the number stack, and then the current operator will be put into the symbol stack. If the priority of the current operator is high
- The operator in the stack is directly found in the symbol.
- 4. When the expression is scanned, pop out the corresponding numbers and symbols from the number floor and symbol stack in sequence and run
- 5. Finally, there is only one number in the number stack, which is the result of the expression
- Verification: 3 + 2 * 6-2 = 13
- Here we will realize the following ideas according to the above ideas
code implementation
package com.hyc.DataStructure.Stack;
/**
* @projectName: DataStructure
* @package: com.hyc.DataStructure.Stack
* @className: Calculator
* @author: Cold Huanyuan doorwatcher
* @description: TODO
* @date: 2021/12/24 20:39
* @version: 1.0
*/
public class Calculator {
public static void main(String[] args) {
// According to the idea of this article, we complete the expression operation of a string of calculations that only include addition, subtraction, multiplication and division
String expression = "3+2*6-2";
/** The calculation idea uses the stack to complete the calculation idea of the expression
* 1.Through an index value (prime index), we traverse our expression
* 2.If we find that it is a number, we will directly enter the number stack
* 3.If it is found that a symbol is scanned, it can be divided into the following situations
* 3.1 If the current symbol stack is found to be empty, it is directly put into the stack
* 3.2 If there are operators on the symbol stack, compare them. If the priority of the current operator is less than or equal to that in the stack
* The operator needs to pop two numbers from the number stack and pop a symbol from the symbol stack for operation,
* The result will be put into the number stack, and then the current operator will be put into the symbol stack. If the priority of the current operator is high
* The operator in the stack is directly found in the symbol.
* 4.When the expression is scanned, pop out the corresponding numbers and symbols from the number floor and symbol stack in sequence and run
* 5.Finally, there is only one number on the number stack, which is the result of the expression
* Verification: 3 + 2 * 6-2 = 13
* Here we will realize the following ideas according to the above ideas
* */
// Create two stacks, one to store the numbers to be calculated and the other to store the symbols to be calculated
ArrayCalStack numStack = new ArrayCalStack(10);
ArrayCalStack operStack = new ArrayCalStack(10);
// Define related variables
int index = 0; //For pointer scanning
int num1 = 0;
int num2 = 0;
int oper = 0;
int res = 0;
//Save the char obtained from each scan to ch
char ch;
//Used for multiple bits
String keepNums = "";
//Start while loop scan expression
while (true) {
// Get every character of expression at once
ch = expression.substring(index, index + 1).charAt(0);
// Determine what ch is (number or symbol) and then operate
if (operStack.isOper(ch)) {
/* If there are operators on the symbol stack, compare them. If the priority of the current operator is less than or equal to that in the stack
* The operator needs to pop two numbers from the number stack and pop a symbol from the symbol stack for operation,
* The result will be put into the number stack, and then the current operator will be put into the symbol stack. If the priority of the current operator is high
* The operator in the stack is directly found in the symbol.*/
//Non null judgment
if (!operStack.isempty()) {
if (operStack.priotrity(ch) <= operStack.priotrity(operStack.peek())) {
num1 = numStack.pop();
num2 = numStack.pop();
oper = operStack.pop();
res = numStack.cal(num1, num2, oper);
// Push the operation result into the number stack
numStack.push(res);
// Then push the current symbol onto the stack, otherwise an operation symbol will be missing
operStack.push(ch);
} else {
//If the priority of the current operator is higher than that of the operator in the stack, it will directly enter the symbol stack
operStack.push(ch);
}
} else {
// If empty, direct access symbol stack
operStack.push(ch);
}
} else {
// If it is a number, go directly to the number stack
/*thinking
* Here we need to consider multi bit numbers when dealing with multi bit numbers
* We need to scan the next bit of this number until we find the next symbol
* At this time, we define a string to splice the number found
* */
// Number of processing bits
keepNums += ch;
// If ch is already the last name of expression, it will be directly put on the stack
if (index == expression.length() - 1) {
numStack.push(Integer.parseInt(keepNums));
} else {
// Judge whether the next character is a number. If so, continue to judge whether it is an operator, and then put it on the stack. Here we want to see whether the end is a symbol
if (operStack.isOper(expression.substring(index + 1, index + 2).charAt(0))) {
//If the last thing is the original acid father, if it is pushed into the stack, our operation change here is keepnums =1 or keepnums =123
numStack.push(Integer.parseInt(keepNums));
// After joining, keep nunms can be cleared for the judgment of the next bit
keepNums = "";
}
}
}
// Let index +1 and judge whether to scan to the end of expression
index++;
if (index >= expression.length()) {
break;
}
}
// When the expression is scanned, pop out the corresponding numbers and symbols from the number stack and symbol stack in sequence, and run
while (true) {
// If the symbol is empty, the final result will be calculated, and there is only one number [result] in the number stack
if (operStack.isempty()) {
break;
}
num1 = numStack.pop();
num2 = numStack.pop();
oper = operStack.pop();
res = numStack.cal(num1, num2, oper);
//Push
numStack.push(res);
}
// pop out the last number of the stack, which is the result
int res2 = numStack.pop();
System.out.printf("expression%s = %d", expression, res2);
}
}
/*
* In order to implement the calculator, we need to write some new functions,
* */
class ArrayCalStack {
//Maximum stack length
private int MaxSize;
//The simulation stack data is placed in this array
private int[] stack;
// Equal to the top of the stack. By default, equal to - 1 represents the bottom part
private int top = -1;
public ArrayCalStack() {
}
// Initialization stack
public ArrayCalStack(int maxSize) {
MaxSize = maxSize;
stack = new int[maxSize];
}
//Returning to the top of the stack only shows that pop does not change the structure of the stack
public int peek() {
return stack[top];
}
//Determine whether the stack is full
public boolean isFull() {
return top == MaxSize - 1;
}
//Determine whether the stack is empty
public boolean isempty() {
return top == -1;
}
//Push data onto stack
public void push(int data) {
if (isFull()) {
System.out.println("Stack full");
return;
}
top++;
stack[top] = data;
}
// Take data out of stack
public int pop() {
if (isempty()) {
throw new RuntimeException("The stack is empty and cannot be taken out");
}
int value = stack[top];
top--;
return value;
}
//When traversing the stack, you need to display data from the top of the stack
public void list() {
if (isempty()) {
System.out.println("The stack is empty");
}
// The output from the top of the stack is actually the output array in reverse order
for (int i = top; i >= 0; i--) {
System.out.printf("stack[%d]=%d\n", i, stack[i]);
}
}
/* Return the priority of the operator. We can set the priority by ourselves and use numbers to represent it
* The higher the number, the higher the priority
* */
public int priotrity(int oper) {
if (oper == '*' || oper == '/') {
return 1;
} else if (oper == '+' || oper == '-') {
return 0;
} else {
return -1;
}
}
// Judge whether it is a character
public boolean isOper(char val) {
return val == '*' || val == '/' || val == '+' || val == '-';
}
// Calculation operations are used to perform operations
public int cal(int num1, int num2, int oper) {
// Store calculation results
int res = 0;
switch (oper) {
case '+':
res = num1 + num2;
break;
case '-':
res = num2 - num1;
break;
case '/':
res = num2 / num1;
break;
case '*':
res = num1 * num2;
break;
default:
break;
}
return res;
}
}Here we implement the basic expression operation, but we don't consider anything
- We implemented the basic calculation, but did not consider the parentheses and so on
- Infix expression is very easy for us to calculate, but it is inconvenient for computer calculation. We will update the suffix expression suitable for computer calculation later