Title Description
Give you an integer n and find how many kinds of binary search trees are composed of exactly n nodes with different node values from 1 to n? Returns the number of binary search trees that meet the meaning of the question.
Example:
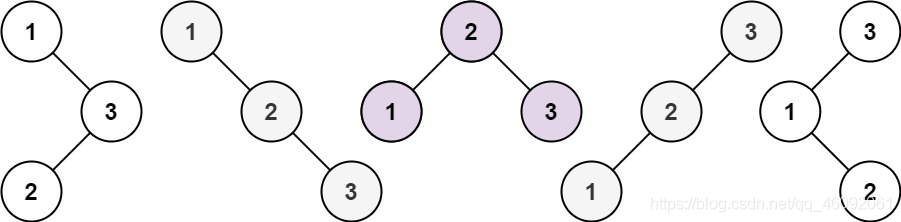
Input: n = 3
Output: 5
dynamic programming
thinking
Given an ordered sequence 1 * n, in order to build a binary search tree, we can traverse each number i, take this number as the tree root, take the 1 * sequence (i − 1) as the left subtree and (i+1) * n sequence as the right subtree. Then we can recursively construct the left subtree and the right subtree in the same way.
In the above construction process, because the root values are different, we can ensure that each binary search tree is unique.
It can be seen that the original problem can be decomposed into two smaller subproblems, and the subproblems can be reused. Therefore, we can think of using dynamic programming to solve this problem.
algorithm
The problem is to calculate the number of different binary search trees. To do this, we can define two functions:
-
G(n): the number of different binary search trees that can be formed by sequences with length n.
-
F(i,n): the number of different binary search trees with i as root and sequence length n (1 ≤ i ≤ n).
It can be seen that G(n) is the function we need to solve.
Later, we will see that G(n) can be obtained from F(i,n), and F(i,n) depends recursively on G(n).
Firstly, according to the idea in the previous section, the total number G(n) of different binary search trees is the sum of F(i,n) traversing all i (1 ≤ i ≤ n). In other words:
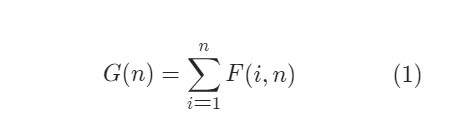
For the boundary case, when the sequence length is 1 (only root) or 0 (empty tree), there is only one case, that is:
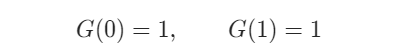
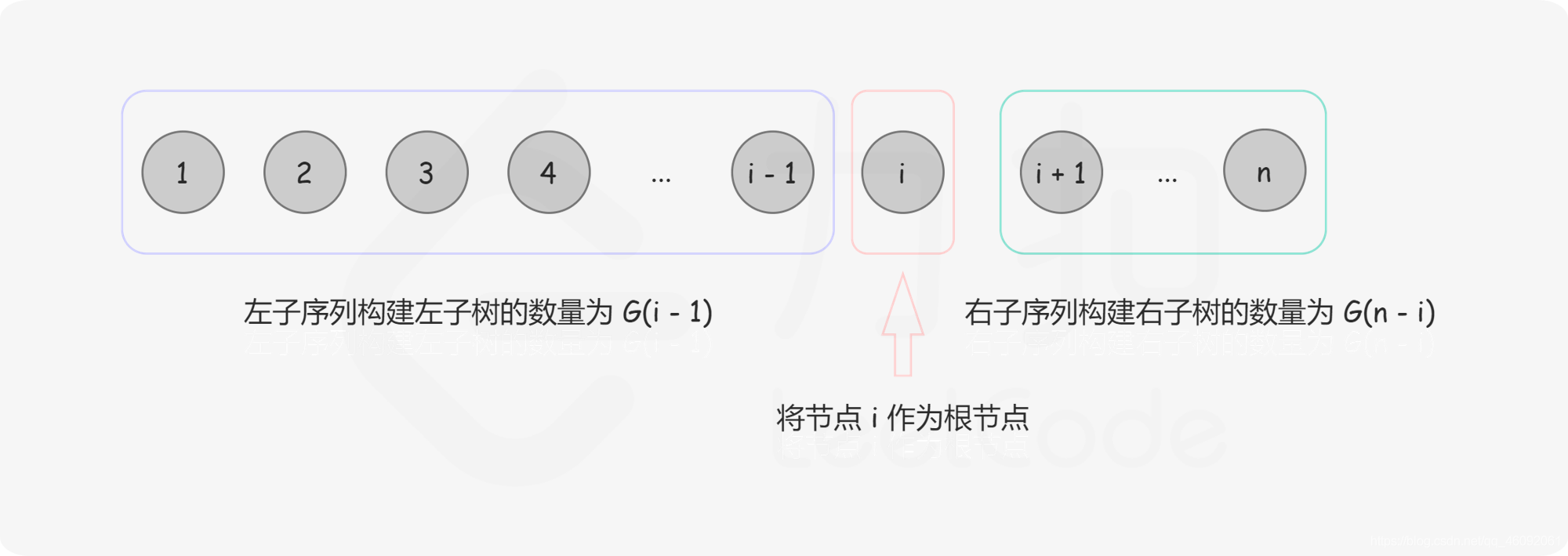
Given the sequence 1 * n, we choose the number i as the root, then the set of all binary search trees with root i is the Cartesian product of the left subtree set and the right subtree set. For each element in the Cartesian product, add the root node to form a complete binary search tree, as shown in the following figure:

Java
class Solution {
public int numTrees(int n) {
int[] G = new int[n + 1];
G[0] = 1;
G[1] = 1;
for (int i = 2; i <= n; ++i) {
for (int j = 1; j <= i; ++j) {
G[i] += G[j - 1] * G[i - j];
}
}
return G[n];
}
}
Python
class Solution:
def numTrees(self, n):
"""
:type n: int
:rtype: int
"""
G = [0]*(n+1)
G[0], G[1] = 1, 1
for i in range(2, n+1):
for j in range(1, i+1):
G[i] += G[j-1] * G[i-j]
return G[n]
Complexity analysis
- Time complexity: O ( n 2 ) O(n^2) O(n2), where n represents the number of nodes of the binary search tree. G(n) function has n values to be solved, and each solution requires O(n) time complexity, so the total time complexity is O ( n 2 ) O(n^2) O(n2).
- Space complexity: O(n). We need O(n) space to store the G array.
mathematics
Ideas and algorithms

Java
class Solution {
public int numTrees(int n) {
// Tip: Here we need to use long type to prevent overflow during calculation
long C = 1;
for (int i = 0; i < n; ++i) {
C = C * 2 * (2 * i + 1) / (i + 2);
}
return (int) C;
}
}
Python
class Solution(object):
def numTrees(self, n):
"""
:type n: int
:rtype: int
"""
C = 1
for i in range(0, n):
C = C * 2*(2*i+1)/(i+2)
return int(C)
Complexity analysis
- Time complexity: O(n), where n represents the number of nodes of the binary search tree. We only need to loop through it once.
- Space complexity: O(1). We only need a constant space to store several variables.
Clever ghost
class Solution {
public:
int numTrees(int n) {
switch(n){
case 1: return 1;
case 2: return 2;
case 3: return 5;
case 4: return 14;
case 5: return 42;
case 6: return 132;
case 7: return 429;
case 8: return 1430;
case 9: return 4862;
case 10: return 16796;
case 11: return 58786;
case 12: return 208012;
case 13: return 742900;
case 14: return 2674440;
case 15: return 9694845;
case 16: return 35357670;
case 17: return 129644790;
case 18: return 477638700;
case 19: return 1767263190;
default: return 0;
}
}
};
(* ̄︶ ̄)