1,Constructing binary tree from preorder and inorder traversal sequences

 

Given the preorder and inorder of a tree. Construct a binary tree and return its root node.

 

Example 1:

 

 

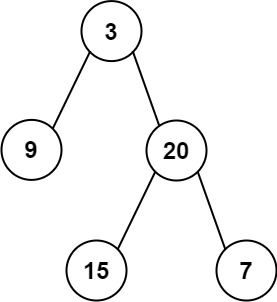
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]
Example 2:

Input: preorder = [-1], inorder = [-1]
Output: [-1]

recursion

Idea: for any tree, the form of preorder traversal is always

[root node, [preorder traversal result of left subtree], [preorder traversal result of right subtree]]

That is, the root node is always the first node in the preorder traversal. The form of middle order traversal is always

[[middle order traversal result of left subtree], root node, [middle order traversal result of right subtree]]

As long as we locate the root node in the middle order traversal, we can know the number of nodes in the left subtree and the right subtree respectively. Since the lengths of preorder traversal and middle order traversal of the same subtree are obviously the same, we can locate all the left and right parentheses in the above form corresponding to the results of preorder traversal.

In this way, we know the pre order traversal and middle order traversal results of the left subtree and the pre order traversal and middle order traversal results of the right subtree. We can recursively construct the left subtree and the right subtree, and then connect the two subtrees to the left and right positions of the root node.

 

Personal words:

The first element of preorder is root. Find root in inorder. Before it, it is the left subtree (long l1), followed by the right subtree (long l2). preorder[1] to preorder[l1] are the left subtree, followed by the right subtree, recursive respectively.

 

details

When locating the root node in the middle order traversal, a simple method is to directly scan the results of the whole middle order traversal and find the root node, but the time complexity is high. We can consider using a hash table to help us quickly locate the root node. For each key value pair in the hash map, The key represents an element (the value of the node), and the value represents its position in the middle order traversal. Before constructing the binary tree, we can scan the list of middle order traversal to construct the hash map. After that, in the process of constructing the binary tree, we only need O(1) to locate the root node.

 

Implementation: python

 1 class Solution:
 2     def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
 3         def myBuildTree(preorder_left: int, preorder_right: int, inorder_left: int, inorder_right: int):
 4             if preorder_left > preorder_right:
 5                 return None
 6             
 7             # The first node in the preorder traversal is the root node
 8             preorder_root = preorder_left
 9             # Locate the root node in the middle order traversal
10             inorder_root = index[preorder[preorder_root]]
11             
12             # First establish the root node
13             root = TreeNode(preorder[preorder_root])
14             # Get the number of nodes in the left subtree
15             size_left_subtree = inorder_root - inorder_left
16             # The left subtree is constructed recursively and connected to the root node
17             # Preorder traversal「From left boundary+1 Beginning size_left_subtree」One element corresponds to the middle order traversal「Locate from the left boundary to the root node-1」Element of
18             root.left = myBuildTree(preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1)
19             # The right subtree is constructed recursively and connected to the root node
20             # Preorder traversal「From left boundary+1+The number of nodes in the left subtree starts at the right boundary」The element of corresponds to the middle order traversal「Locate from root node+1 To right border」Element of
21             root.right = myBuildTree(preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right)
22             return root
23         
24         n = len(preorder)
25         # Construct hash mapping to help us quickly locate the root node
26         index = {element: i for i, element in enumerate(inorder)}
27         return myBuildTree(0, n - 1, 0, n - 1)

 

 

2,Constructing binary tree from middle order and post order traversal sequences

Similarly:

 1 class TreeNode(object):
 2     def __init__(self, val=0, left=None, right=None):
 3         self.val = val
 4         self.left = left
 5         self.right = right
 6 
 7 
 8 class Solution(object):
 9     def buildTree(self, inorder, postorder):
10         """
11         :type inorder: List[int]
12         :type postorder: List[int]
13         :rtype: TreeNode
14         """
15 
16         def build(post_left, post_right, in_left, in_right):
17             if post_left > post_right:
18                 return None
19 
20             post_root = post_right  # 4
21             in_root = mp_ind[postorder[post_root]]  # 1
22 
23             root = TreeNode(postorder[post_root])
24             right_size = in_right - in_root # 3
25             root.left = build(post_left, post_right-right_size-1, in_left, in_root-1)
26             root.right = build(post_right-right_size, post_right-1, in_root+1, in_right)
27 
28             return root
29 
30         n = len(inorder)
31         mp_ind = {val: i for i, val in enumerate(inorder)}
32 
33         return build(0, n - 1, 0, n - 1)