The ideas related to this blog post are included in exercise 3-79 in Chapter 7 of C + + self study notes (Volume I) facing the process. This book has not been published yet, so any pictures, tables, codes and articles related to the book (including this article) are not allowed to be reproduced.

Only the source file sumofintegers CPP program 1 should not be difficult for beginners.

//sumOfIntegers.cpp
#include <iostream>    //cout, endl
using std::cout;    using std::endl;
int main()
{
    int sum=0, lastAdded=0;    //And value, the last added value
    for(int value=1; value<=100; value+=1)
    {
        sum+=value;
        lastAdded=value;
    }
    cout<<"sum is "<<sum<<endl;
    cout<<"last added is "<<lastAdded<<endl;
    return 0;
}

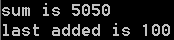
The function of the program is to calculate the sum of the first 100 positive integers, and the expected sum value is 5050. It is expected that the last added value should be positive integer 100. The implementation results are consistent with the expected results:

Once there was such a curious student who reduced all the data of the program to 1% of the original, and changed all the data types from integer type to single precision floating-point number type. What was the result? Try the following only from the source file sumofsingerfloating CPP program 2,

//sumOfSingleFloatings.cpp
#include <iostream>    //cout, endl
using std::cout;    using std::endl;
int main()
{
    float sum=0.0f, lastAdded=0.0f;    //And value, the last added value
    for(float value=0.01f; value<=1.0f; value+=0.01f)
    {
        sum+=value;
        lastAdded=value;
    }
    cout<<"sum is "<<sum<<endl;
    cout<<"last added is "<<lastAdded<<endl;
    return 0;
}

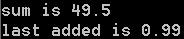
The function of the program is to calculate 0.01F + 0.02f ++ For the sum of 1.0f, the expected sum value is 50.5f, and the expected value added last should be 1.0f. However, the implementation results are not completely consistent with the expected results,

The student continues to try to improve the data accuracy and change all single precision data to double precision data. What will be the result? Try the following only from the source file sumofdoublefloatings CPP program 3,

//sumOfDoubleFloatings.cpp
#include <iostream>    //cout, endl
using std::cout;    using std::endl;
int main()
{
    double sum=0.0, lastAdded=0.0;            //And value, the last added value
    for(double value=0.01; value<=1.0; value+=0.01)
    {
        sum+=value;
        lastAdded=value;
    }
    cout<<"sum is "<<sum<<endl;
    cout<<"last added is "<<lastAdded<<endl;
    return 0;
}

The function of the program is: calculate 0.01 + 0.02 ++ For the sum of 1.0, the expected sum value is 50.5, and the last added value is expected to be 1.0. However, the implementation results are completely inconsistent with the expected results,

Why does the data accuracy improve, but the execution result deviates more from the expected result?  

To answer this question, we need to use the skills introduced in the previous blog post to reveal the actual stored values of 0.01f and 0.01. Change the above procedure 2 to the following, which is only composed of sumofsinglefloatings2 CPP program 4,

//sumOfSingleFloatings2.cpp
#include <iomanip>     //setprecision, setw
#include <iostream>    //cout, endl, fixed, streamsize
using std::cout;            using std::endl;    using std::fixed;
using std::setprecision;    using std::setw;    using std::streamsize;
int main()
{
    const streamsize shorterWidth=14,       //Shorter field width value
                        precision=32,       //double-precision value
             longerWidth=precision+3;       //Longer field width value
    cout<<fixed<<setprecision(precision);   //Outputs floating-point numbers in a fixed-point format with 32 decimal places
    float sum=0.0f, lastAdded=0.0f;         //And value, the last added value
    cout<<setw(shorterWidth)<<"0.01f is "<<setw(longerWidth)<<0.01f<<endl;
    for(float value=0.01f; value<=1.0f; value+=0.01f)
    {
        sum+=value;
        lastAdded=value;
    }
    cout<<setw(shorterWidth)<<"sum is "<<setw(longerWidth)<<sum<<endl;
    cout<<setw(shorterWidth)<<"last added is "<<setw(longerWidth)<<lastAdded<<endl;
    return 0;
}

The results are as follows:,

It can be seen that the actual stored value of 0.01f is 0.009999997764825820928515625, which is less than the expected stored value of 0.01. The errors between them are gradually accumulated and amplified in the process of continuous cyclic summation. After 99 cycles, when the value is increased by 0.01f 99 times from 0.01f, the value becomes 0.999993448907470703125, which is less than the expected value of 1.0. Therefore, continue to execute the 100th cycle, and the value less than 1.0 is the "last added value". This error also results in a final sum of 50.4999847412109375, which is less than the expected sum of 50.5.

Similarly, change program 3 to the following only by the source file sumofdoublefloatings2 CPP program 5,

//sumOfDoubleFloatings2.cpp
#include <iomanip>     //setprecision, setw
#include <iostream>    //cout, endl, fixed, streamsize
using std::cout;            using std::endl;    using std::fixed;
using std::setprecision;    using std::setw;    using std::streamsize;
int main()
{
    const streamsize shorterWidth=14,       //Shorter field width value
                        precision=64,       //double-precision value
             longerWidth=precision+3;       //Longer field width value
    cout<<fixed<<setprecision(precision);   //Outputs floating-point numbers in a fixed-point format with 32 decimal places
    double sum=0.0, lastAdded=0.0;          //And value, the last added value
    cout<<setw(shorterWidth)<<"0.01 is "<<setw(longerWidth)<<0.01<<endl;
    for(double value=0.01; value<=1.0; value+=0.01)
    {
        sum+=value;
        lastAdded=value;
    }
    cout<<setw(shorterWidth)<<"sum is "<<setw(longerWidth)<<sum<<endl;
    cout<<setw(shorterWidth)<<"last added is "<<setw(longerWidth)<<lastAdded<<endl;
    return 0;
}

The results are as follows:,

It can be seen that the actual stored value of 0.01 is 0.010000000000000000 2081668171721685132943093776702880859375, which is greater than the expected stored value of 0.01. The errors between them are gradually accumulated and amplified in the process of continuous cyclic summation. After 98 cycles, when value is increased by 0.01 98 times from 0.01, its value becomes 0.990000000000000657252030578092671930789509765625, which is greater than the expected value of 0.99. Thus, after the 99th cycle is executed, when value is added by 0.01 for the 99th time, the obtained value will be greater than the expected value of 1.0, so the cycle ends immediately. The value greater than the expected value of 1.0 is not added to the sum value as expected, and the 100th cycle is not executed as expected. The final sum value is 49.5000000000000 28421709430404007434844970703125, greater than 49.5.

Summary: since the actual storage value of 0.01f is less than the expected storage value, 100 cycles are executed as expected, so the actual sum value is slightly less than the expected sum value of 50.5. Since the actual stored value of 0.01 is greater than the expected stored value, only 99 cycles are executed (100 cycles are not executed as expected), the actual sum value is greater than the expected sum value of sum equation (0.01 + 0.02 +... + 0.99) by 49.5. In short, when selecting a loop count variable, it is recommended to use integer type instead of floating-point type.