Count the number of prime numbers in [2,n) interval.

1. Enumeration

[2,n) start traversing from 2 and judge whether it is a prime number one by one.

#include <bits/stdc++.h> 
using namespace std;
const int N = 1e5+5;
int prime[N];		//Prime array holds prime numbers 
int isPrime(int n)	//Judge whether n is a prime number. A prime number returns 1, not 0
{
	for(int i=2;i*i<=n;i++){
		if(n % i == 0) return 0;
	}
	return 1;
}
int main() 
{
	int n;
	cin>>n;
	int res = 0;
	for(int i=2;i<n;i++){
		if(isPrime(i)) prime[res++] = i;
	}
	//Output prime 
	cout<<res<<'\n';
	for(int i=0;i<res;i++) cout<<prime[i]<<" ";	
    return 0;
}

Time complexity: O(n √ n)

2. Elsevier sieve

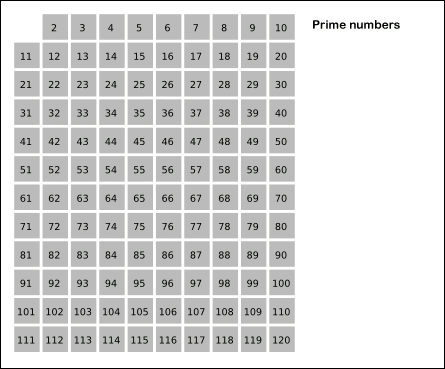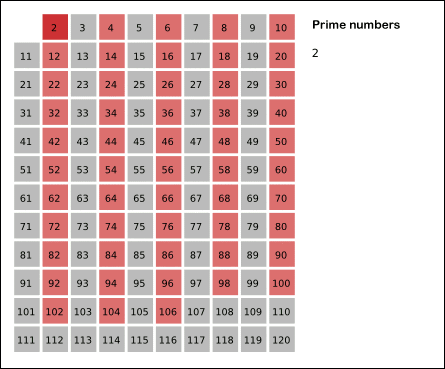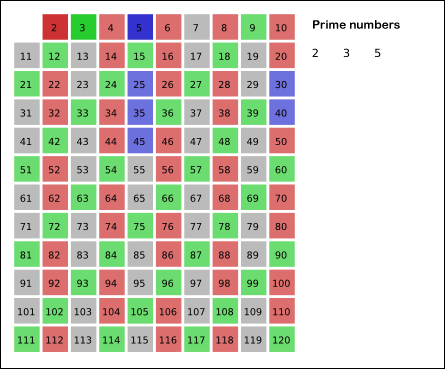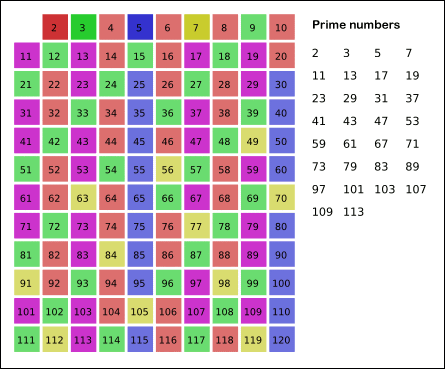
[2,n) start traversing from 2. 2 is a prime number, write it down and cross out all multiples of 2; next 3 is a prime number, write it down and cross out all multiples of 3; 4 is a multiple of 2, which has been crossed out, so next is 5, 5 is a prime number, write it down and cross out all multiples of 5; push it to N in this way.

There is a dynamic diagram that can intuitively understand this screening method.

 

#include <bits/stdc++.h> 
using namespace std;
const int N = 1e5+5;
int prime[N];	//The prime array records the status. 1 is a prime, and 0 is not a prime
int res = 0;	//res record prime number 
int main() 
{
	int n;
	cin>>n;
	memset(prime,1,sizeof(prime));	//Initialize the prime array to 1
	for(int i=2;i<n;i++){
		if(prime[i]){
			res++;
			for(int j=2*i;j<n;j+=i) prime[j] = 0;	//All multiples of i are not prime numbers, and the status is updated to 0
		}
	}
	//Output prime 
	cout<<res<<'\n';
	for(int i=2;i<n;i++){
		if(prime[i]) cout<<i<<" ";
	}
    return 0;
}

Time complexity: O(n ㏒ n ㏒ n)

3. Linear screen

During the traversal of the sieve, repeated marking will occur. For example, if 30 is both a multiple of 2 and a multiple of 3 or a multiple of 5, it will be marked once when traversing all multiples of 2, once again when traversing multiples of 3, and once again when traversing multiples of 5. It can be optimized, but there will still be the number marked repeatedly, while the linear sieve can achieve a completely non repetitive solution.

Each composite number can be written as the product of prime numbers in a unique form. In other words, a composite number can be expressed as the product of a prime number and a number.

So if (I% prime [J] = = 0) break;

For example, for chestnuts, i=8, I% 2 = = 0, so for i=8, you only need to check prime[1]=2, because for prime numbers greater than prime[1], for example, 3, 8 * 3 = 2 * 4 * 3 = 12 * 2, that is, 24 (8 * 3 = 24) does not need to be checked at 8, but only at 12.

reference resources https://blog.csdn.net/leolin_/article/details/6642126

#include <bits/stdc++.h> 
using namespace std;
const int N = 1e5+5;
int prime[N];	//Prime array holds prime numbers
int res = 0;	//res record prime number 
int vis[N];		//0 is prime, 1 is not prime 
int main() 
{
	int n;
	cin>>n;
	for(int i=2;i<n;i++){
		if(!vis[i]) prime[res++] = i;	//Store primes in array 
		for(int j=0;j<res&&i*prime[j]<n;j++){
			vis[i*prime[j]] = 1;
			if(i % prime[j] == 0) break;	//Encountered i smallest prime factor 
		}
	}
	cout<<res<<'\n';
	for(int i=0;i<res;i++){
		cout<<prime[i]<<" ";
	}
//	for(int i=2;i<n;i++){
//		if(!vis[i]) cout<<i<<" ";
//	}
    return 0;
}

Time complexity: O(n)

4. Odd sieve

It is known that even numbers are not necessarily prime numbers, but prime numbers must be odd numbers, so you only need to mark the composite numbers in the odd range, and the remaining odd numbers are prime numbers.

In addition, odd * odd = odd, odd * even = even.

According to the above conditions, the optimization can be carried out on the basis of the existing Ehrlich sieve. You can choose i+=2 to avoid even numbers during traversal, or you can directly change all even numbers in the status array to 0.

#include <bits/stdc++.h> 
using namespace std;
const int N = 1e5+5;
int prime[N];	//The prime array records the status. 1 is a prime, and 0 is not a prime
int res = 0;	//res record prime number 
int main() 
{
	int n;
	cin>>n;
//	memset(prime,0,sizeof(prime));
	prime[2] = 1; 	
	for(int i=3;i<n;i++){
		if(i%2 == 1) prime[i] = 1;	//The odd number is marked as 1 
		else prime[i] = 0;			//Even number marked as 0 
	}
	for(int i=2;i<n;i++){
		if(prime[i]){
			res++;
			for(int j=2*i;j<=n;j+=i) prime[j] = 0;
		}
	}
	//Output prime 
	cout<<res<<'\n';
	for(int i=2;i<n;i++){
		if(prime[i]) cout<<i<<" ";
	}
    return 0;
}