realization
public class SelectionSort {
public int[] selectionSort(int[] A, int n) {
//Record minimum subscript value
int min=0;
for(int i=0; i<A.length-1;i++){
min = i;
//Find the minimum value after the beginning of subscript i
for(int j=i+1;j<A.length;j++){
if(A[min]>A[j]){
min = j;
}
}
if(i!=min){
swap(A,i,min);
}
}
return A;
}
private void swap(int[] A,int i,int j){
int temp = A[i];
A[i] = A[j];
A[j] = temp;
}
}
The working principle of the insertion sorting algorithm is to construct an ordered sequence, scan the unordered data from back to front in the sorted sequence, find the corresponding position and insert it. Therefore, in the process of scanning from back to front, it is necessary to repeatedly move the sorted elements backward step by step to provide insertion space for the latest elements
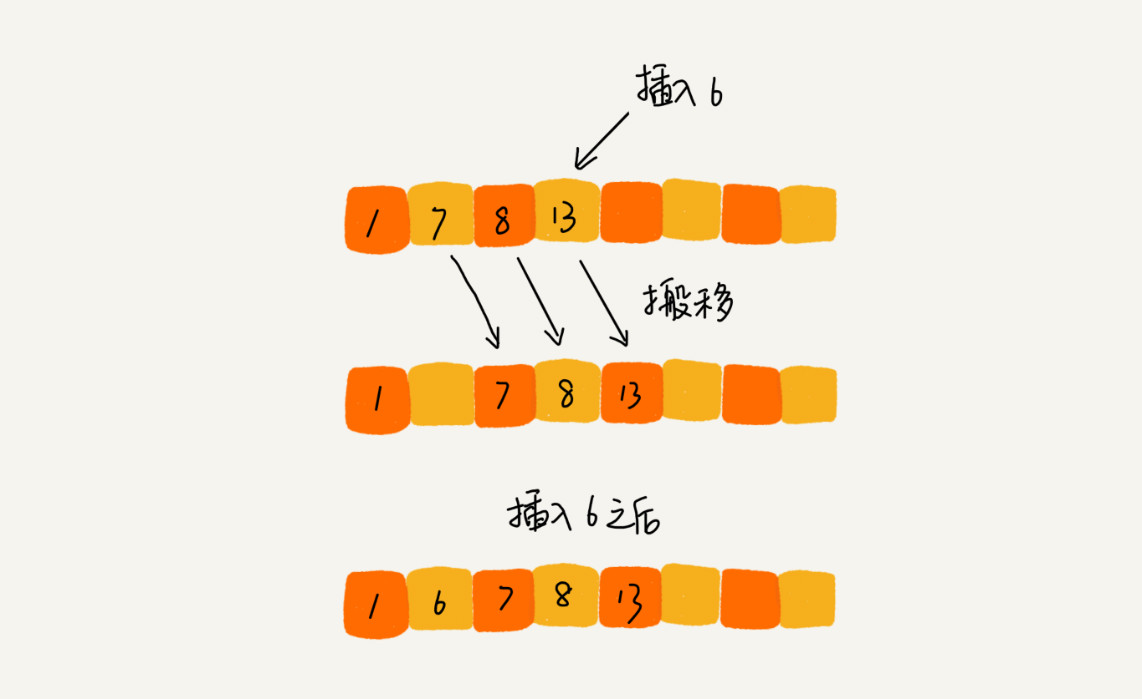
realization
public class InsertionSort {
public int[] insertionSort(int[] A, int n) {
//The idea of inserting playing cards with simulation
//Inserted playing cards
int i,j,temp;
//One has been inserted, continue to insert
for(i=1;i<n;i++){
temp = A[i];
//Move all the cards in front of i that are larger than the card to be inserted one bit back, leaving one bit free for the new card
for(j=i;j>0&&A[j-1]>temp;j--){
A[j] = A[j-1];
}
//Fill the empty one with the inserted card
A[j] = temp;
}
return A;
}
}
The core of merge sort is the idea of divide and conquer. First divide the array into the front and back parts from the middle, then sort the front and back parts respectively, and then merge the two parts in good order, so that the whole array is in order
If two ordered tables are merged into one, it is called two-way merging
Merge sort is a stable sort algorithm
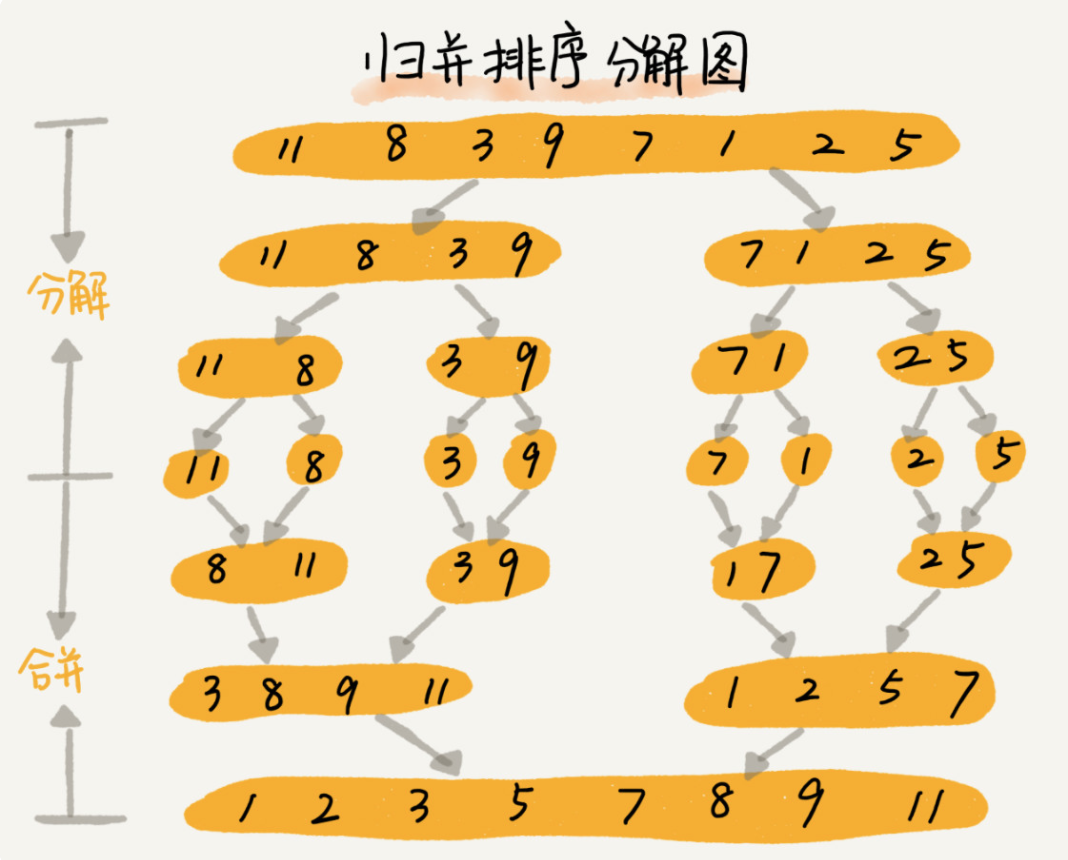
realization
public class MergeSort {
public static void main(String[] args) {
int data[] = { 9, 5, 6, 8, 0, 3, 7, 1 };
megerSort(data, 0, data.length - 1);
System.out.println(Arrays.toString(data));
}
public static void mergeSort(int data[], int left, int right) { // Both ends of the array
if (left < right) { // Equal means that there is only one number and there is no need to dismantle it
int mid = (left + right) / 2;
mergeSort(data, left, mid);
mergeSort(data, mid + 1, right);
// After splitting, we will merge, that is, we will recursively return
merge(data, left, mid, right);
}
}
public static void merge(int data[], int left, int mid, int right) {
int temp[] = new int[data.length]; //A temporary array is used to hold the merged data
int point1 = left; //Indicates the position of the first number on the left
int point2 = mid + 1; //Indicates the position of the first number on the right
int loc = left; //It means where we are now
while(point1 <= mid && point2 <= right){
if(data[point1] < data[point2]){
temp[loc] = data[point1];
point1 ++ ;
loc ++ ;
}else{
temp[loc] = data[point2];
point2 ++;
loc ++ ;
}
}
while(point1 <= mid){
temp[loc ++] = data[point1 ++];
}
while(point2 <= right){
temp[loc ++] = data[point2 ++];
}
for(int i = left ; i <= right ; i++){
data[i] = temp[i];
}
}
}
Basic idea:
Firstly, the number of a group to be sorted is divided into several groups according to a certain increment d (n/2, n is the number of numbers to be sorted). The subscript difference of records in each group is d, and all elements in each group are directly inserted and sorted, and then a smaller increment is used (d/2) group it, and then perform direct insertion sorting in each group. When the increment is reduced to 1, the sorting is completed after direct insertion sorting
Hill sort method (reduced increment method) belongs to insertion sort. It is a method to divide the whole non sequence into several small subsequences for insertion sort respectively
If the length of the array is 10, the array elements are 25, 19, 6, 58, 34, 10, 7, 98, 160 and 0
The algorithm process of hill sorting is as follows:
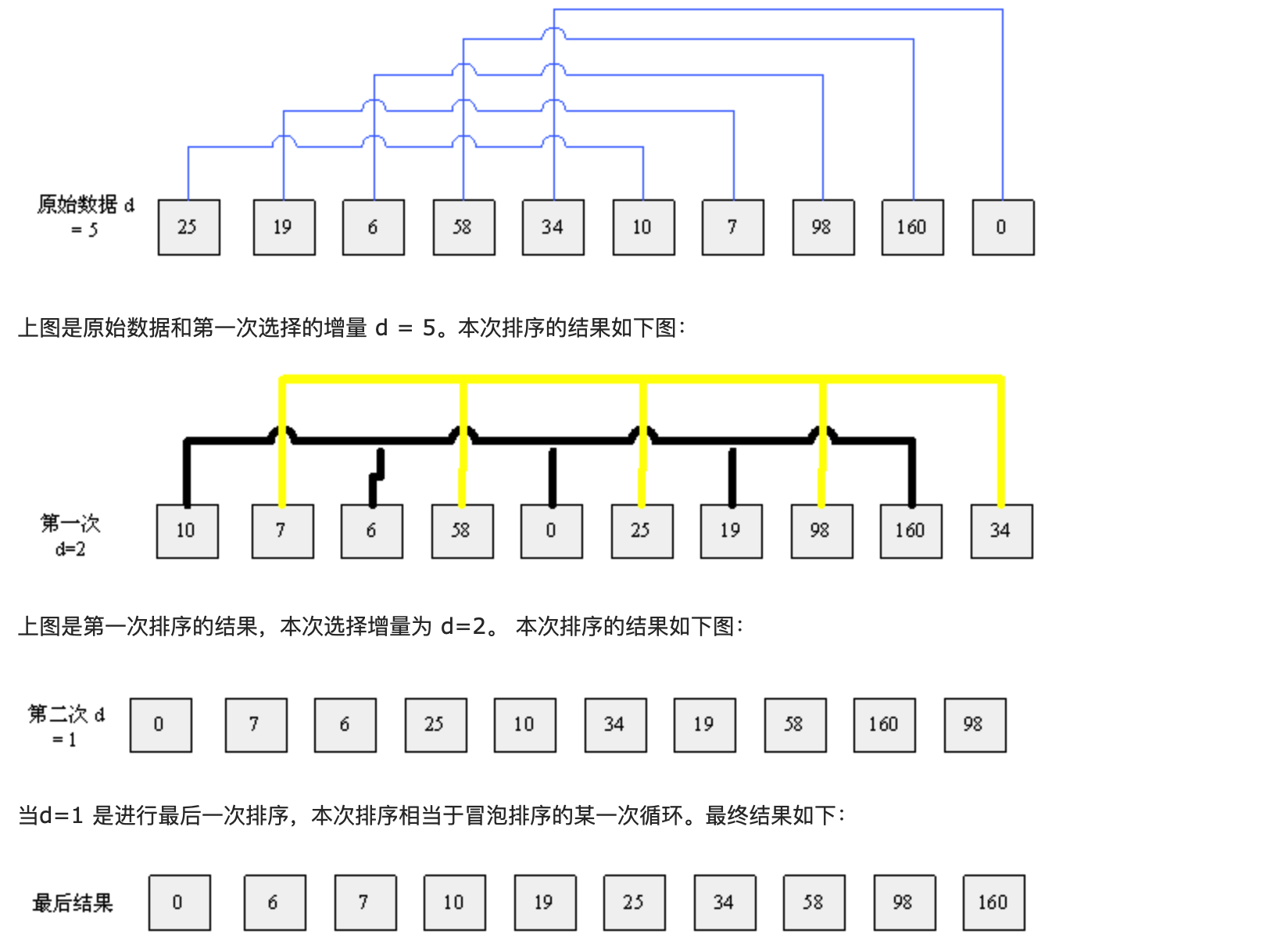
realization
public static int[] ShellSort(int[] array) {
int len = array.length;
int temp, gap = len / 2;
while (gap > 0) {
for (int i = gap; i < len; i++) {
temp = array[i];
int preIndex = i - gap;
while (preIndex >= 0 && array[preIndex] > temp) {
array[preIndex + gap] = array[preIndex];
preIndex -= gap;
}
array[preIndex + gap] = temp;
}
gap /= 2;
}
return array;
}
Basic idea of quick sort: divide the records to be arranged into two independent parts through one-time sorting. If the keywords of one part of the records are smaller than those of the other part, the two parts of the records can be sorted separately to achieve the order of the whole sequence
-
First, take a number from the sequence as the reference number.
-
In the partition process, all numbers larger than this number are placed on its right, and all numbers less than or equal to it are placed on its left.
-
Repeat the second step for the left and right intervals until there is only one number in each interval.

Implementation 1
public class QuickSort {
public static void quickSort(int[]arr,int low,int high){
if (low < high) {
int middle = getMiddle(arr, low, high);
quickSort(arr, low, middle - 1);//Recursive left
quickSort(arr, middle + 1, high);//Recursive right
}
}
public static int getMiddle(int[] list, int low, int high) {
int tmp = list[low];
while (low < high) {
while (low < high && list[high] >= tmp) {//Greater than the keyword is on the right
high--;
}
list[low] = list[high];//If less than the keyword, switch to the left
while (low < high && list[low] <= tmp) {//Less than the keyword is on the left
low++;
}
list[high] = list[low];//If it is greater than the keyword, switch to the left
}
list[low] = tmp;
return low;
}
}
Implementation 2
public class QuickSort {
public static void quickSort(int data[], int left, int right) {
int base = data[left]; // Benchmark number, take the first of the sequence
int ll = left; // It shows the position from the left
int rr = right; // Indicates the position to find from the right
while (ll < rr) {
// Find a number smaller than the benchmark number from the back
while (ll < rr && data[rr] >= base) {
rr--;
}
if (ll < rr) { // It means finding something bigger than it
int temp = data[rr];
data[rr] = data[ll];
data[ll] = temp;
ll++;
}
while (ll < rr && data[ll] <= base) {
ll++;
}
if (ll < rr) {
int temp = data[rr];
data[rr] = data[ll];
data[ll] = temp;
rr--;
}
}
// It must be that recursion is divided into three parts. Continue to quickly arrange left and right. Pay attention to adding conditions, otherwise recursion will overflow the stack
if (left < ll)
quickSort(data, left, ll - 1);
if (ll < right)
quickSort(data, ll + 1, right);
}
}
optimization
Basic quick sort selects the first or last element as the benchmark. However, this has been a very bad way to deal with it
If the array is already ordered, the segmentation at this time is a very bad segmentation. Because each partition can only reduce the sequence to be sorted by one, this is the worst case, and the quick sort is reduced to bubble sort, with a time complexity of O(n^2)
Triple median
The general practice is to use the median of the three elements at the left end, right end and center as the hub element
For example, the sequence to be sorted is 8 1 4 9 6 3 5 2 7 0
8 on the left, 0 on the right and 6 in the middle
After we sort the three numbers here, the middle number is used as the pivot, and the pivot is 6
Insert sort
When the length of the sequence to be sorted is divided to a certain size, insert sorting is used. Reason: for small and partially ordered arrays, it is better to arrange quickly than to arrange well. When the length of the sequence to be sorted is divided to a certain size, the efficiency of continuous segmentation is worse than that of insertion sorting. At this time, interpolation can be used instead of fast sorting
Repeating array
After one split, you can gather the elements equal to the key together. When you continue the next split, you don't need to split the elements equal to the key
After a partition, the elements equal to the key are gathered together, which can reduce the number of iterations and improve the efficiency
Specific process: there are two steps in the processing process
The first step is to put the elements equal to key into both ends of the array during the partition process
The second step is to move the element equal to the key around the pivot after the division
give an example:
Sequence to be sorted 1 4 6 7 6 6 7 6 8 6
Select pivot from three values: Number 6 with subscript 4
After conversion, the sequence to be divided: 6 4 6 7 1 6 7 6 8 6
Pivot key: 6
The first step is to put the elements equal to key into both ends of the array during the partition process
The result is: 6 4 1 6 (pivot) 7 8 7 6 6 6
At this point, all elements equal to 6 are placed at both ends
The second step is to move the element equal to the key around the pivot after the division
The result is: 1 4 6 6 6 (pivot) 6 6 6 7 8 7
At this point, all elements equal to 6 are moved around the pivot
After that, fast sorting was performed in two subsequences: 1,4 and 7,8,7
Heap is a special kind of tree. As long as these two points are met, it is a heap.
-
Heap is a complete binary tree;
-
The value of each node in the heap must be greater than or equal to (or less than or equal to) the value of each node in its subtree.
The heap whose value of each node is greater than or equal to the value of each node in the subtree is called "large top heap".
The heap whose value of each node is less than or equal to the value of each node in the subtree is called "small top heap".
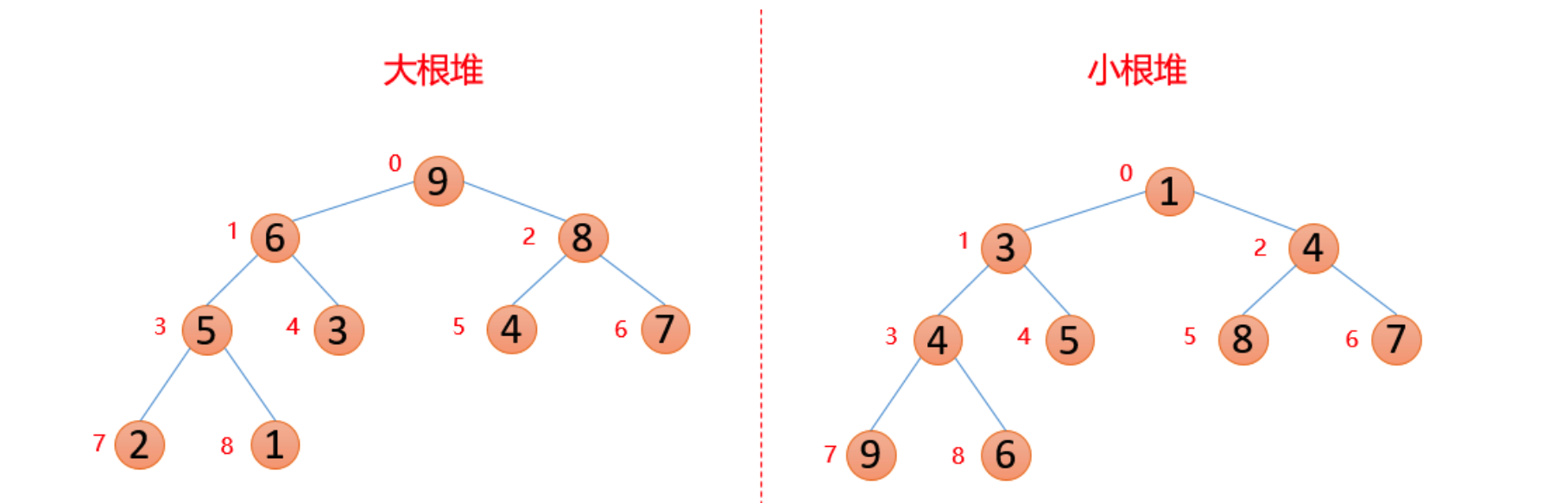
Generally, large root heap is used in ascending order and small root heap is used in descending order
How to implement a heap
A complete binary tree is more suitable for storing arrays. Using an array to store a complete binary tree is very memory saving. Because we do not need to store the pointers of the left and right child nodes, we can find the left and right child nodes and parent nodes of a node simply through the subscript of the array.
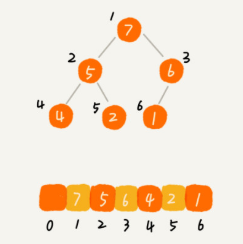
For example, find the parent node and left and right child nodes of a number in array arr, such as the number with known index i
-
Parent node index: (i-1)/2 (here, divide by 2 in the computer and omit the decimal)
-
Left child index: 2*i+1
-
Right child index: 2*i+2
Therefore, the definition and nature of heap:
-
Large root pile: arr (I) > arr (2 * I + 1) & & arr (I) > arr (2 * I + 2)
-
Small root pile: arr (I) < arr (2 * I + 1) & & arr (I) < arr (2 * I + 2)
last
Due to space constraints, Xiaobian cuts out several diagrams of knowledge explanation here, and the program ape (yuan) in need can praise it Stamp here to get all the information for free Get oh



For example, find the parent node and left and right child nodes of a number in array arr, such as the number with known index i
-
Parent node index: (i-1)/2 (here, divide by 2 in the computer and omit the decimal)
-
Left child index: 2*i+1
-
Right child index: 2*i+2
Therefore, the definition and nature of heap:
-
Large root pile: arr (I) > arr (2 * I + 1) & & arr (I) > arr (2 * I + 2)
-
Small root pile: arr (I) < arr (2 * I + 1) & & arr (I) < arr (2 * I + 2)
last
Due to space constraints, Xiaobian cuts out several diagrams of knowledge explanation here, and the program ape (yuan) in need can praise it Stamp here to get all the information for free Get oh
[external chain picture transferring... (img-hBn9LJrq-1628293219717)]
[external chain picture transferring... (img-kZZcbSy6-1628293219718)]
[external chain pictures are being transferred... (img-fiOao87a-1628293219719)]
[external chain picture transferring... (img-ApK8ACpt-1628293219721)]
[external chain picture transferring... (img-th3OKQyn-1628293219723)]