Data structure - stack (Chapter 3) sorting notes. If there are errors, please correct them.
Sequence table
Single linked list

Stack of base book exercise do ( " & " surface show lead use transfer use ) . { I n i t S t a c k ( & S ) : first beginning turn one individual empty Stack S . S t a c k E m p t y ( S ) : sentence break one individual Stack yes no by empty ， if Stack S by empty be return return t r u e ， no be return return f a l s e . P u s h ( & S , x ) : enter Stack ， if Stack S not full ， be take x plus enter send of become by new Stack top . P o p ( & S , & x ) : Out Stack ， if Stack S wrong empty ， be elastic Out Stack top element element ， and use x return return . G e t T o p ( S , & x ) : read Stack top element element ， if Stack S wrong empty ， be use x return return top element element . D e s t r o y S t a c k ( & S ) : pin ruin Stack ， and Buddhism discharge Stack S occupy use of Save Store empty between . Basic operation of stack ("\ &" means reference call). \Begin {cases} initstack (\ & S): initialize an empty stack\ StackEmpty(S): determines whether a stack is empty. If stack s is empty, it returns true; otherwise, it returns false\ Push (\ & S, x): enter the stack. If stack s is not full, add x to make it the top of the new stack\ Pop (\ & S, \ & x): exit the stack. If stack s is not empty, the top element of the stack will pop up and return with X\ Gettop (s, \ & x): read the top element of the stack. If stack s is not empty, use X to return the top element\ Destroy stack (\ & S): destroy the stack and free the storage space occupied by stack s\ \end{cases} The basic operation of stack ("&" means reference call). ⎩⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧ initstack: initialize an empty stack s. StackEmpty(S): determines whether a stack is empty. If stack s is empty, it returns true; otherwise, it returns false. Push & S, X: enter the stack. If stack s is not full, add x to make it the top of the new stack. Pop & S, & x): out of the stack. If stack s is not empty, the top element of the stack will pop up and return with X. Gettop (s, & x): read the top element of the stack. If stack s is not empty, use X to return the top element. Destroy & stack: destroy the stack and free the storage space occupied by stack s. ​

Sequential storage structure of stack

Sequential storage type description of stack

#define MaxSize 50 / / defines the maximum number of elements in the stack
typedef struct
{
	ElemType data[MaxSize]; //Store elements in the stack
	int top; //Stack top pointer
}SqStack;

• Compare the sequential storage type description of the linear table:

#define MaxSize 50 / / defines the maximum length of a linear table
typedef struct //Creating structure types with typedef
{
	ElmeType data[MaxSize]; //Elements of the sequence table
	int length; //Current length of sequence table
}SqList; //Type definition of sequence table

& initialize - initstack

void InitStack(SqStack& S)
{
	S.top = -1; //Initialize stack top pointer
}

analysis:

• Stack top pointer: S.top, initially set S.top=-1; Stack top element: S.data[S.top]
• Initially, S.top can also be defined as 0, that is, S.top=0. It is equivalent to specifying that top points to the next storage unit of the top element of the stack.

Stack empty (s)

bool StackEmpty(SqStack S)
{
	return S.top == -1;
}

• If S.top is initially defined as 0, the null condition is return S.top==0;

analysis:

• When the initial S.top is set to - 1 - stack empty condition: S.top==-1; Stack full condition: S.top==MaxSize-1; Stack length: S.top+1.
• When the initial S.top is set to 0 - stack empty condition: S.top==0; Stack full condition: S.top==MaxSize; Stack length: S.top.

& stack push

bool Push(SqStack& S, ElemType x)
{
	if (S.top == MaxSize - 1) return false; //Stack full, error reported
	S.data[++S.top] = x; //The pointer is incremented by 1 before entering the stack
	return true;
}

• If S.top is initially defined as 0:

bool Push(SqStack& S, ElemType x)
{
	if (S.top == MaxSize) return false; //Stack full, error reported
	S.data[S.top++] = x; //Stack first, add 1 to the pointer,
	return true;
}

analysis:

• When the initial S.top is set to - 1 - stacking operation: when the stack is not full, the stack top pointer first adds 1, and then sends the value to the stack top element.
• When the initial S.top is set to 0 - stack feeding operation: when the stack is not full, first send the value to the top element of the stack, and then increase the top pointer by 1.
• Since the stack operation of sequential stack is constrained by the upper bound of the array, when the estimation of the maximum use space of the stack is insufficient, stack overflow may occur. At this time, the message should be reported to the user in time for timely processing and avoiding errors.

& out of stack pop

bool Pop(SqStack& S, ElemType& x)
{
	if (S.top == -1) return false; //Stack empty, error reported
	x = S.data[S.top--]; //First out of the stack, and then minus 1
	return true;
}

• If S.top is initially defined as 0:

bool Pop(SqStack& S, ElemType& x)
{
	if (S.top == 0) return false; //Stack empty, error reported
	x = S.data[--S.top]; //The pointer is subtracted by 1 before it is out of the stack
	return true;
}

analysis:

• When the initial S.top is set to - 1 - stack out operation: when the stack is not empty, first take the value of the top element of the stack, and then reduce the top pointer by 1.
• When the initial S.top is set to 0 - stack out operation: when the stack is not empty, first reduce the stack top pointer by 1, and then take the value of the stack top element.

Read stack top element - gettop (s, &x)

bool GetTop(SqStack S, ElemType& x)
{
	if (S.top == -1) return false; //Stack empty, error reported
	x = S.data[S.top]; //x record stack top element
	return false;
}

analysis:

• Only to read the top element of the stack, there is no out of stack operation, so the original top element of the stack remains in the stack.

& Destroy - destrorystack

void DestoryStack(SqStack*& S) //Destroy stack
{
	free(S);
}

analysis:

• malloc() and free() functions must be paired. If the malloc () function is used to allocate space, it needs to be released with the free () function.

Complete code (static stack)

#include<iostream>
using namespace std;
#define MaxSize 10 / / defines the maximum number of elements in the stack
typedef int ElemType;
typedef struct
{
	ElemType data[MaxSize]; //Store elements in the stack
	int top; //Stack top pointer
}SqStack;

void InitStack(SqStack& S) //Initialization stack
{
	S.top = -1; //Initialize stack top pointer
}

bool StackEmpty(SqStack S) //Determine whether the stack is empty
{
	return S.top == -1;
}

bool Push(SqStack& S, ElemType x) //Push 
{
	if (S.top == MaxSize - 1) return false; //Stack full, error reported
	S.data[++S.top] = x; //The pointer is incremented by 1 before entering the stack
	return true;
}

bool Pop(SqStack& S, ElemType& x) //Out of stack
{
	if (S.top == -1) return false; //Stack empty, error reported
	x = S.data[S.top--]; //First out of the stack, and then minus 1
	return true;
}

bool GetTop(SqStack S, ElemType& x) //Get stack top element
{
	if (S.top == -1) return false; //Stack empty, error reported
	x = S.data[S.top]; //x record stack top element
	return false;
}

int main() //Main function
{
	SqStack S;
	int a[MaxSize] = { 2,4,8,0,1,6,7,3,9,5 };
	InitStack(S);
	cout << boolalpha << "Is the stack empty? -" << StackEmpty(S) << endl;
	for (int i = 0; i < MaxSize; i++)
		Push(S, a[i]);
	cout << boolalpha << "Is the stack empty? -" << StackEmpty(S) << endl;
	ElemType topnum;
	GetTop(S, topnum);
	cout << "Stack top elements are:" << topnum << endl;
	ElemType num;
	cout << "Take out the elements in the stack in turn:";
	for (int i = 0; i < MaxSize; i++)
	{
		Pop(S, num);
		cout << num<<' ';
	}
	return 0;
}

Complete code (dynamic stack)

#include<iostream>
#include<malloc.h>
using namespace std;
#define MaxSize 10 / / defines the maximum number of elements in the stack
typedef int ElemType;
typedef struct
{
	ElemType data[MaxSize]; //Store elements in the stack
	int top; //Stack top pointer
}SqStack;

bool InitStack(SqStack*& S)
{
	S = (SqStack*)malloc(sizeof(SqStack)); //Allocate a sequential stack space, and store the first address in s
	if (S == NULL) return false; //Insufficient memory, allocation failed
	S->top = -1; //The stack top pointer is set to - 1
	return true;
}

bool StackEmpty(SqStack* S)
{
	return S->top == -1;
}

bool Push(SqStack*& S, ElemType x)
{
	if (S->top == MaxSize - 1) return false; //When the stack is full, that is, overflow on the stack
	S->top++; //Stack top pointer increases by 1
	S->data[S->top] = x; //The element x is placed at the pointer at the top of the stack
	return true;
}

bool Pop(SqStack*& S, ElemType& x)
{
	if (S->top == -1) return false; //The stack is empty, that is, overflow under the stack
	x = S->data[S->top]; //Get stack top element
	S->top--; //Stack top pointer minus 1
	return true;
}

bool GetTop(SqStack* S, ElemType& x)
{
	if (S->top == -1) return false; //The stack is empty, that is, overflow under the stack
	x = S->data[S->top]; //Get stack top element
	return true;
}

void DestoryStack(SqStack*& S) //Destroy stack
{
	free(S);
}

int main() //Main function
{
	SqStack *S;
	//The remaining code is the same as the static stack

analysis:

• Static stack:
  Advantages: simple implementation.
  Disadvantages: the stack size is fixed. When the space is full, it cannot be saved again, or the space given is too large to waste space
• Dynamic stack
  Advantages: the size is not fixed. When the memory is insufficient, you can open up space yourself
  Disadvantages: compared with static stack, the code implementation is complex and error prone

Shared stack

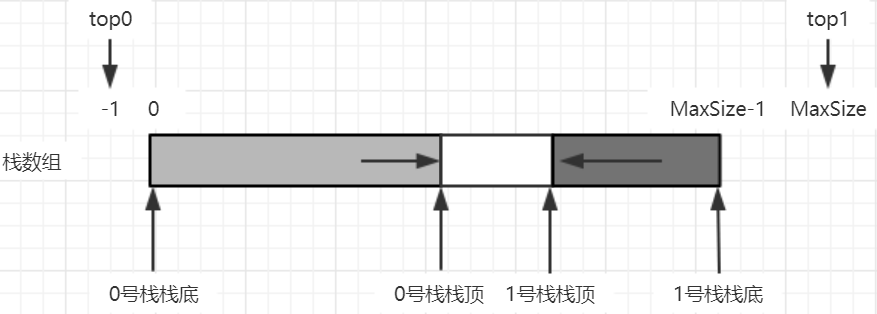
• Using the characteristic that the position of the bottom of the stack is relatively unchanged, two sequential stacks can share a one-dimensional array space. The bottom of the two stacks are set at both ends of the shared space, and the top of the two stacks extends to the middle of the shared space.
  

• Shared stack is to make more effective use of storage space. The space of the two stacks is adjusted to each other. Overflow occurs only when the whole storage space is occupied. The time complexity of accessing data is O(1), so it has no impact on the access efficiency.

• Stack empty condition: top0==-1 when stack 0 is empty; Stack 1 is empty, top==MaxSize.
• Stack full condition: top0==top1-1.
• Element x stacking operation: stacking = Top0 + +; data[top0]=x； Stack 1 operation as Top1 –; data[top1]=x.
• Stack out operation: stack out 0 operation as x=data[top0]; top0–； The stack 1 operation is x=data[top1]; top1++.
• In the above settings, the data array represents the storage space of the shared stack, and top0 and top1 are the stack top pointers of the two stacks respectively. In this way, the shared stack is identified by data, top0 and top1, or they can be designed as a structure type:

typedef struct
{
	ElemType data [Maxsize]; //Store elements in the shared stack
	int topl, top2; //Top pointer of two stacks
}DStack; ///Type of shared stack

• When implementing the basic operation algorithm of shared stack, you need to add a formal parameter i to indicate which stack to operate on. For example, i=0 means to operate on stack 0, and i=1 means to operate on stack 1.

Chain storage structure of stack

• The advantage of chain stack is that there is no overflow when the stack is full. All operations of the specified stack are carried out in the header of the single linked list (because it is very convenient to insert a new node and delete the first node after the given chain stack, and the time complexity of the corresponding algorithm is O(1)).
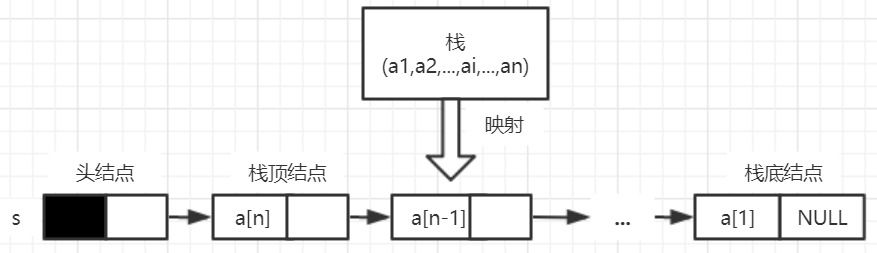
• The head node refers to the chain stack with s, the first node is the top node of the stack, and the tail node is the bottom node of the stack. The elements in the stack are a1,a2,..., an from the bottom of the stack to the top of the stack.
• The node type LinkStNode in the chain stack is declared as follows:

typedef struct linknode
{
	Elemtype data; //Data domain
	struct linknode *next; //Pointer field
}LinkstNode; //Chain stack node type

• In the chain stack with s as the head node pointer (referred to as chain stack s), four elements that are very important for the later algorithm design can be summarized.
• Stack empty condition: S - > next = = null.
• Stack full condition: because the stack is full only when memory overflows, it is usually not considered, so it can be regarded as non stack full in the stack.
• Stack operation of element e: create a new node to store element e (pointed to by p), and insert node p after the header.
• Stack out operation: take out the data value of the first node and delete it.

& initialize - initstack

void InitStack(LinkStNode *&S)
{
	S = (LinkStNode*)malloc(sizeof(LinkStNode));
	S->next = NULL;
}

Stack empty (s)

bool StackEmpty(LinkStNode *S)
{
	return S->next == NULL;
}

& stack push

bool Push(LinkStNode*& S, ElemType e)
{
	LinkStNode* p;
	p = (LinkStNode*)malloc(sizeof(LinkStNode)); //New node p
	if (p == NULL) return false; //Insufficient memory, allocation failed
	p->data = e; //Store element e
	p->next = S->next; //Insert the p node as the first node
	S->next = p;
}

& out of stack pop

bool Pop(LinkStNode*& S, ElemType& e)
{
	LinkStNode* p;
	if (S->next == NULL) return false; //Stack empty
	p = S->next; //p points to the first node
	e = p->data; //Extract the value of the first node
	S->next = p->next; //Delete first node
	free(p); //Release the storage space of the deleted node
	return true;
}

Read stack top element - gettop (s, &x)

bool GetTop(LinkStNode *S, ElemType& e)
{
	if (S->next == NULL) return false; //Stack empty
	e = S->next->data; //Extract the value of the first node
	return true;
}

& Destroy - destrorystack

void DestoryStack(LinkStNode*& S)
{
	LinkStNode* p = S->next, * pre = S; //pre points to the head node and p points to the head node
	while (p != NULL) //Loop to p is empty
	{
		free(pre); //Release pre node
		pre = p; //pre, p synchronization backward
		p = p->next;
	}
	free(pre); //At this point, pre points to the tail node to free up its space
}

Complete code: chain stack (leading node)

#include<iostream>
#include<malloc.h>
using namespace std;
typedef int ElemType;
typedef struct LinkNode
{
	ElemType data;
	struct LinkNode* next;
}LinkStNode;

void InitStack(LinkStNode *&S)
{
	S = (LinkStNode*)malloc(sizeof(LinkStNode));
	S->next = NULL;
}

bool StackEmpty(LinkStNode *S)
{
	return S->next == NULL;
}

bool Push(LinkStNode*& S, ElemType e)
{
	LinkStNode* p;
	p = (LinkStNode*)malloc(sizeof(LinkStNode)); //New node p
	if (p == NULL) return false; //Insufficient memory, allocation failed
	p->data = e; //Store element e
	p->next = S->next; //Insert the p node as the first node
	S->next = p;
}

bool Pop(LinkStNode*& S, ElemType& e)
{
	LinkStNode* p;
	if (S->next == NULL) return false; //Stack empty
	p = S->next; //p points to the first node
	e = p->data; //Extract the value of the first node
	S->next = p->next; //Delete first node
	free(p); //Release the storage space of the deleted node
	return true;
}

bool GetTop(LinkStNode *S, ElemType& e)
{
	if (S->next == NULL) return false; //Stack empty
	e = S->next->data; //Extract the value of the first node
	return true;
}

void DestoryStack(LinkStNode*& S)
{
	LinkStNode* p = S->next, * pre = S; //pre points to the head node and p points to the head node
	while (p != NULL) //Loop to p is empty
	{
		free(pre); //Release pre node
		pre = p; //pre, p synchronization backward
		p = p->next;
	}
	free(pre); //At this point, pre points to the tail node to free up its space
}

int main()
{
	LinkStNode *S;
	InitStack(S);
	cout << boolalpha << "Is the stack empty? -" << StackEmpty(S) << endl;
	for(int i=0;i<10;i++)
		Push(S, i);
	cout << boolalpha << "Is the stack empty? -" << StackEmpty(S) << endl;
	ElemType topnum;
	GetTop(S, topnum);
	cout << "Stack top elements are:" << topnum << endl;
	ElemType num;
	cout << "Take out the elements in the stack in turn:";
	for (int i = 0; i < 10; i++)
	{
		Pop(S, num);
		cout << num << ' ';
	}
	return 0;
}

Complete code: chain stack (no leading node)

#include<iostream>
#include<malloc.h>
using namespace std;
typedef int ElemType;
typedef struct LinkNode
{
	ElemType data;
	struct LinkNode* next;
}LinkStNode;

void InitStack(LinkStNode *&S)
{
	S = (LinkStNode*)malloc(sizeof(LinkStNode));
	S = NULL;
}

bool StackEmpty(LinkStNode *S)
{
	return S == NULL;
}

bool Push(LinkStNode*& S, ElemType e)
{
	LinkStNode* p;
	p = (LinkStNode*)malloc(sizeof(LinkStNode)); //New node p
	if (p == NULL) return false; //Insufficient memory, allocation failed
	p->data = e; //Store element e
	p->next = S;
	S = p;
}

bool Pop(LinkStNode*& S, ElemType& e)
{
	LinkStNode* p = S;
	if (S == NULL) return false; //Stack empty
	e = p->data; //Extract the value of the first node
	S= p->next; //Delete first node
	free(p); //Release the storage space of the deleted node
	return true;
}

bool GetTop(LinkStNode *S, ElemType& e)
{
	if (S == NULL) return false; //Stack empty
	e = S->data; //Extract the value of the first node
	return true;
}

void DestoryStack(LinkStNode*& S)
{
	LinkStNode* p = S, * pre = S->next; //pre points to the head node and p points to the head node
	while (p != NULL) //Loop to p is empty
	{
		free(pre); //Release pre node
		pre = p; //pre, p synchronization backward
		p = p->next;
	}
	free(pre); //At this point, pre points to the tail node to free up its space
}

analysis:

• Except that the time complexity of destroying the stack is O(n), the time complexity of other operations is O(1).