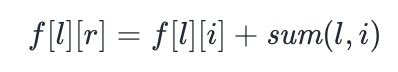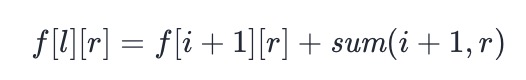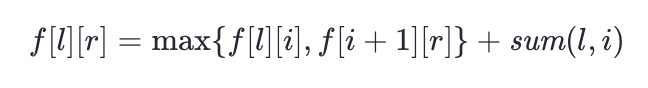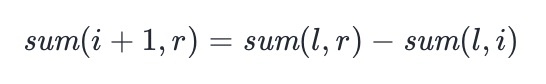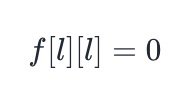1, Title Description

• Several stones are arranged in a row. Each stone has an associated value. The associated value is an integer, which is given by the array stoneValue.
• Each round of the game: Alice will divide the line of stones into two non empty lines (i.e. the left line and the right line); Bob is responsible for calculating the value of each row, that is, the sum of the values of all stones in this row. Bob will discard the row with the largest value, and Alice's score is the value of the remaining row (accumulated in each round). If the values of the two rows are equal, Bob asks Alice to decide which row to discard, and the next round starts with the remaining row.
• When there is only one stone left, the game ends and Alice's score is initially 0.
• Returns the maximum score Alice can get.
• Example 1:

Input: stoneValue = [6,2,3,4,5,5]
Output: 18
 Explanation: in the first round, Alice Divide rows into [6，2，3]，[4，5，5] . The left row has a value of 11 and the right row has a value of 14. Bob Discarded the right line, Alice My score is now 11.
In the second round, Alice Divide rows into [6]，[2，3] . This time Bob Throw away the left row, Alice The score becomes 16 (11) + 5). 
Last round Alice Only rows can be divided into [2]，[3] . Bob Throw away the right row, Alice Your score is now 18 (16) + 2). The game is over because there is only one stone left in this line.

• Example 2:

Input: stoneValue = [7,7,7,7,7,7,7]
Output: 28

• Example 3:

Input: stoneValue = [4]
Output: 0

2, Solving algorithm

① Dynamic programming

• Use f[l][r] to represent the maximum score Alice can get when she faces the continuous stone from position l to r in the array stoneValue. Since Alice needs to choose to divide this section of stones into two parts, we can enumerate the separation positions i. the stones in the left part are from positions l to i, and the stones in the right part are from positions i+1 to r. Note sum(l,r) represents the sum of the scores of stones from position l to r. according to the requirements of the topic:
• • If sum (L, I) < sum (I + 1, R), Bob will discard the right part, and the state transition equation is:

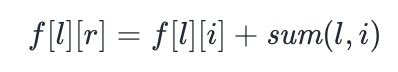
• • If sum (L, I) > sum (I + 1, R), Bob will discard the left part, and the state transition equation is:

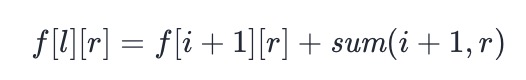
• • If sum(l,i)=sum(i+1,r), Bob will let Alice select the discarded part, and the state transition equation is:

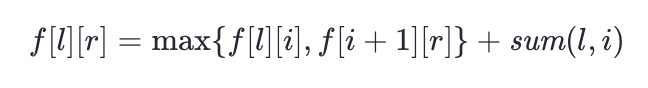
• The value of sum(l,r) can be calculated in advance. You can use prefix and or directly traverse the calculation method. When enumerating i, we can calculate the value of sum(l,i) at the same time, so that the value of sum(i+1,r) can be obtained at the time of O(1) through the following formula:

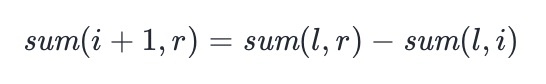
• When there is only one stone left, Alice's score is 0, and the corresponding boundary conditions are:

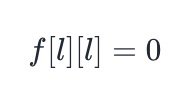
• The final answer is f[0][n − 1], where n is the length of the array stoneValue.
• If the triple loop enumeration l, r, i is used for state transition, the code of C + + language may exceed the time limit. Therefore, the code given below uses the top-down memory search method to complete dynamic planning. In this way, you can skip some states that do not need to be calculated and pass the problem in a reasonable time.
• C example:

class Solution {
private:
    vector<vector<int>> f;

public:
    int dfs(const vector<int>& stoneValue, int left, int right) {
        if (left == right) {
            return 0;
        }
        if (f[left][right]) {
            return f[left][right];
        }

        int sum = accumulate(stoneValue.begin() + left, stoneValue.begin() + right + 1, 0);
        int suml = 0;
        for (int i = left; i < right; ++i) {
            suml += stoneValue[i];
            int sumr = sum - suml;
            if (suml < sumr) {
                f[left][right] = max(f[left][right], dfs(stoneValue, left, i) + suml);
            } else if (suml > sumr) {
                f[left][right] = max(f[left][right], dfs(stoneValue, i + 1, right) + sumr);
            } else {
                f[left][right] = max(f[left][right], max(dfs(stoneValue, left, i), dfs(stoneValue, i + 1, right)) + suml);
            }
        }
        return f[left][right];
    }

    int stoneGameV(vector<int>& stoneValue) {
        int n = stoneValue.size();
        f.assign(n, vector<int>(n));
        return dfs(stoneValue, 0, n - 1);
    }
};

• Java example:

class Solution {
    int[][] f;

    public int stoneGameV(int[] stoneValue) {
        int n = stoneValue.length;
        f = new int[n][n];
        return dfs(stoneValue, 0, n - 1);
    }

    public int dfs(int[] stoneValue, int left, int right) {
        if (left == right) {
            return 0;
        }
        if (f[left][right] != 0) {
            return f[left][right];
        }

        int sum = 0;
        for (int i = left; i <= right; ++i) {
            sum += stoneValue[i];
        }
        int suml = 0;
        for (int i = left; i < right; ++i) {
            suml += stoneValue[i];
            int sumr = sum - suml;
            if (suml < sumr) {
                f[left][right] = Math.max(f[left][right], dfs(stoneValue, left, i) + suml);
            } else if (suml > sumr) {
                f[left][right] = Math.max(f[left][right], dfs(stoneValue, i + 1, right) + sumr);
            } else {
                f[left][right] = Math.max(f[left][right], Math.max(dfs(stoneValue, left, i), dfs(stoneValue, i + 1, right)) + suml);
            }
        }
        return f[left][right];
    }
}

• Complexity analysis:
• • Time complexity: O(n3), where n is the length of the array stoneValue.
• • Space complexity: O(n2), the space required to store all States.

② Recursion + memorization

• Let f(L,R) be the maximum score that can be obtained on the row of stones of stoneValue[L:R]; Obviously, f(1,N) is the answer. So what about f(1,N)? The answer shows recursion.
• • Termination condition: obviously, when L == R, you can directly obtain the answer, which is 0, so take L == R as the termination condition.
• • Progressive stage: enumerate the segmentation strategies from L to R, and then retain the maximum value of f(L,i) + sum(L,i), or f(i+1,R) + sum(i+1, R) according to the meaning of the topic.
• • Regression stage: use the optimal solution obtained in the progressive stage to update f(L,R).
• In addition, because repeated subproblems will occur in the solution process, it is necessary to avoid repeated calculation by memory method.
• C + + example:

class Solution {
public:
    int64_t dp[501][501]; // Memorized array to avoid double counting
    int64_t sum[501];
    
    int64_t dfs(int L, int R) {
        if(dp[L][R] != -1) { // This sub question has been calculated. Direct range answer
            return dp[L][R];
        }
        if(L == R) { // Terminate the condition and get the answer directly
            dp[L][R] = 0;
        } else {
            // In the progressive stage, the maximum value is solved according to the meaning of the question;
            int64_t val = 0;
            for(int i = L; i< R; i++) {
                int64_t s1 = sum[i] - sum[L-1];
                int64_t s2 = sum[R] - sum[i];
                
                if(s1 < s2) { // According to the meaning of the question, only the second half can be taken
                    val = max(val, s1 + dfs(L, i));
                } else if(s1 > s2){ // According to the meaning of the question, only the first half can be taken
                    val = max(val, s2 + dfs(i+1, R));
                } else { // When equal, it can be selected arbitrarily~
                    val = max(val, max(dfs(L, i), dfs(i+1, R)) + s1);
                }
            }
            // In the regression stage, update the answer
            dp[L][R] = val;
        }
        return dp[L][R];
    }
    
    int stoneGameV(vector<int>& stoneValue) {
        memset(dp, -1, sizeof(dp));
        
        // Come out, prefix and
        sum[0] = 0;
        for(int i = 0; i < stoneValue.size(); i++) {
            sum[i+1] = sum[i] + stoneValue[i];
        }
        
        return dfs(1, stoneValue.size());    
    }
};