This paper is a continuation of the introduction to self driving cars final project-w7_pid to realize vehicle lateral and longitudinal control, which aims to change the vehicle lateral controller to Pure pursuit mode. (it is the last project assignment in the first part of Coursera automatic driving series courses)
Introduction to Pure Pursuit
Pure tracking and its variants are often used in mobile robot path tracking problems, and are often used in autopilot cars. The main idea is to calculate the radius of curvature between the rear axle center and the desired tracking point (target point) of the vehicle, and then obtain the steering wheel angle or front wheel angle required for the tracking path.
The target point is determined by the forward looking distance ld from the current rear axle position to the desired path. The target point (gx, gy) is shown in the figure.

Use the target point position and the angle between the vehicle heading vector and the forward-looking vector α To determine the steering angle of the vehicle δ . According to the sine theorem, the following formula is obtained:

Why is the first formula 2 α? Because in this mathematical model, the vehicle trajectory is approximately an arc. At the position of the rear axle point, the rear axle orientation is tangent to the arc. Because the center of the circle, the center of the rear axle and the target point constitute an isosceles triangle, it can be concluded that the angle is 2 α. In the last equation κ Is the curvature of the arc. According to the bicycle model of Ackerman steering vehicle, the steering angle can be written as:

According to the above two formulas, the rotation angle formula is obtained:
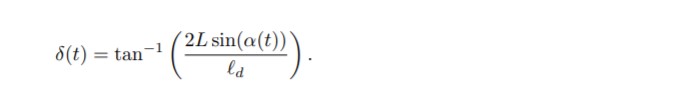
By defining a new variable, the control law can be better understood. eld represents the lateral distance between the heading vector and the target point, and the formula is obtained:

In this case, the curvature formula can be written as:

This formula shows that pure tracking is actually a proportional controller that calculates the angle of rotation according to the tracking error of a certain forward-looking distance ld in front of the vehicle, and the gain of the controller is 2/ld^2.
In practice, the stable gain (forward-looking distance) will be adjusted according to different speeds, which is well understood. Referring to human drivers, when the vehicle speed changes, the distance to be observed is different, which also leads to ld being specified as a function of vehicle speed. Rewrite the control law as follows:
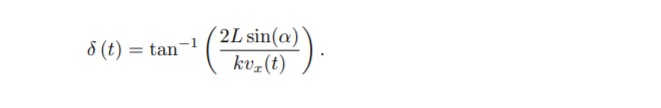
Here, it is a common practice to use the longitudinal speed of the vehicle to control the forward-looking distance in proportion. In addition, the forward-looking distance is usually saturated at the minimum and maximum values.
These are most of the formulas for pure tracking control.
Pure tracking lateral controller in Final project
Similarly, similar to the previous article, the pure tracking controller is separated into a class.
Specific implementation:
#pure_pursuit.py
import numpy as np
class PP(object):
def __init__(self,L, k, k_Ld):
self.L = L
self.k = k
self.k_Ld = k_Ld
def update(self, coeffs, velocity):
'''
coeffs: The coefficient of fitting the tracking curve is used to calculate eld
'''
eps = 0.001
if velocity < eps:
steering_angle = 0.0
else:
# For Pure Pursuit if we look ahead distance changes, then the cte changes
Ld_x = self.k_Ld * velocity
cte = np.polyval(coeffs, Ld_x)
alpha = np.arctan(cte/Ld_x)
sin_alpha = np.sin(alpha)
steering_angle = np.arctan((2*self.L* sin_alpha) / (self.k * velocity))
return steering_angle
contorller2d.py
Similarly, the controlle2d is simply modified, mainly to initialize the PP controller, and then use the PP controller to update the steering wheel angle.
#controller2d.py
#!/usr/bin/env python3
"""
2D Controller Class to be used for the CARLA waypoint follower demo.
"""
import cutils
import numpy as np
from pid import PID
from pure_pursuit import PP
class Controller2D(object):
def __init__(self, waypoints):
self.vars = cutils.CUtils()
self._current_x = 0
self._current_y = 0
self._current_yaw = 0
self._current_speed = 0
self._desired_speed = 0
self._current_frame = 0
self._current_timestamp = 0
self._start_control_loop = False
self._set_throttle = 0
self._set_brake = 0
self._set_steer = 0
self._waypoints = waypoints
self._conv_rad_to_steer = 180.0 / 70.0 / np.pi
self._pi = np.pi
self._2pi = 2.0 * np.pi
## PID
self.throttle_brake_pid = PID(P=7.0, I=1.0, D=1.026185)
self.throttle_brake_pid.setSampleTime = 0.033
## Pure Pursuit
self.pp = PP(L=4.5, k=1.00, k_Ld=1.3)
def update_values(self, x, y, yaw, speed, timestamp, frame):
self._current_x = x
self._current_y = y
self._current_yaw = yaw
self._current_speed = speed
self._current_timestamp = timestamp
self._current_frame = frame
if self._current_frame:
self._start_control_loop = True
def update_desired_speed(self):
min_idx = 0
min_dist = float("inf")
desired_speed = 0
for i in range(len(self._waypoints)):
dist = np.linalg.norm(
np.array([
self._waypoints[i][0] - self._current_x,
self._waypoints[i][1] - self._current_y
]))
if dist < min_dist:
min_dist = dist
min_idx = i
if min_idx < len(self._waypoints) - 1:
desired_speed = self._waypoints[min_idx][2]
self.target_wp = self._waypoints[min_idx]
else:
desired_speed = self._waypoints[-1][2]
self.target_wp = self._waypoints[-1]
self._desired_speed = desired_speed
def update_waypoints(self, new_waypoints):
self._waypoints = new_waypoints
def get_commands(self):
return self._set_throttle, self._set_steer, self._set_brake
def set_throttle(self, input_throttle):
# Clamp the throttle command to valid bounds
throttle = np.fmax(np.fmin(input_throttle, 1.0), 0.0)
self._set_throttle = throttle
def set_steer(self, input_steer_in_rad):
# Covnert radians to [-1, 1]
input_steer = self._conv_rad_to_steer * input_steer_in_rad
# Clamp the steering command to valid bounds
steer = np.fmax(np.fmin(input_steer, 1.0), -1.0)
self._set_steer = steer
def set_brake(self, input_brake):
# Clamp the steering command to valid bounds
brake = np.fmax(np.fmin(input_brake, 1.0), 0.0)
self._set_brake = brake
def map_coord_2_Car_coord(self, x, y, yaw, waypoints):
wps = np.squeeze(waypoints)
wps_x = wps[:, 0]
wps_y = wps[:, 1]
num_wp = wps.shape[0]
## create the Matrix with 3 vectors for the waypoint x and y coordinates w.r.t. car
wp_vehRef = np.zeros(shape=(3, num_wp))
cos_yaw = np.cos(-yaw)
sin_yaw = np.sin(-yaw)
wp_vehRef[0, :] = cos_yaw * (wps_x - x) - sin_yaw * (wps_y - y)
wp_vehRef[1, :] = sin_yaw * (wps_x - x) + cos_yaw * (wps_y - y)
return wp_vehRef
def update_controls(self):
######################################################
# RETRIEVE SIMULATOR FEEDBACK
######################################################
x = self._current_x
y = self._current_y
yaw = self._current_yaw
v = self._current_speed
self.update_desired_speed()
v_desired = self._desired_speed
t = self._current_timestamp
waypoints = self._waypoints
throttle_output = 0
steer_output = 0
brake_output = 0
######################################################
######################################################
# MODULE 7: DECLARE USAGE VARIABLES HERE
######################################################
######################################################
"""
Use 'self.vars.create_var(<variable name>, <default value>)'
to create a persistent variable (not destroyed at each iteration).
This means that the value can be stored for use in the next
iteration of the control loop.
Example: Creation of 'v_previous', default value to be 0
self.vars.create_var('v_previous', 0.0)
Example: Setting 'v_previous' to be 1.0
self.vars.v_previous = 1.0
Example: Accessing the value from 'v_previous' to be used
throttle_output = 0.5 * self.vars.v_previous
"""
self.vars.create_var('v_previous', 0.0)
# Skip the first frame to store previous values properly
if self._start_control_loop:
"""
Controller iteration code block.
Controller Feedback Variables:
x : Current X position (meters)
y : Current Y position (meters)
yaw : Current yaw pose (radians)
v : Current forward speed (meters per second)
t : Current time (seconds)
v_desired : Current desired speed (meters per second)
(Computed as the speed to track at the
closest waypoint to the vehicle.)
waypoints : Current waypoints to track
(Includes speed to track at each x,y
location.)
Format: [[x0, y0, v0],
[x1, y1, v1],
...
[xn, yn, vn]]
Example:
waypoints[2][1]:
Returns the 3rd waypoint's y position
waypoints[5]:
Returns [x5, y5, v5] (6th waypoint)
Controller Output Variables:
throttle_output : Throttle output (0 to 1)
steer_output : Steer output (-1.22 rad to 1.22 rad)
brake_output : Brake output (0 to 1)
"""
wps_vehRef = self.map_coord_2_Car_coord(x, y, yaw, waypoints)
wps_vehRef_x = wps_vehRef[0, :]
wps_vehRef_y = wps_vehRef[1, :]
## fit a 3rd order polynomial to the waypoints
coeffs = np.polyfit(wps_vehRef_x, wps_vehRef_y, 7)
#vel_poly = np.polyfit(wps_vehRef_x, wps_vehRef_y, 3)
## get cross-track error from fit
# In vehicle coordinates the cross-track error is the intercept at x = 0, That means that since we have a fit of the form:
# Y = C0 + C1*X + C2*X^2 + C3X^3 + ....
# when we evaluate using x=0 we just get C0.
# But to understand where this is coming from I like to keep the whole evaluation, even though this is exactly C0
CarRef_x = CarRef_y = CarRef_yaw = 0.0
# For Pure Pursuit if we look ahead a distance Ld = nnnn then the cte changes
cte = np.polyval(coeffs, CarRef_x) - CarRef_y
# get orientation error from fit ( Since we are trying a 3rd order poly, then, f' = a1 + 2*a2*x + 3*a3*x2)
# in this case and since we moved our reference sys to the Car, x = 0 and also yaw = 0
yaw_err = CarRef_yaw - np.arctan(coeffs[1])
speed_err = v_desired - v
######################################################
######################################################
# MODULE 7
# LONGITUDINAL CONTROLLER
# AND
# LATERAL CONTROLLER HERE
######################################################
######################################################
"""
Implement a longitudinal controller here. Remember that you can
access the persistent variables declared above here. For
example, can treat self.vars.v_previous like a "global variable".
"""
"""
Implement a lateral controller here. Remember that you can
access the persistent variables declared above here. For
example, can treat self.vars.v_previous like a "global variable".
"""
#### PID ####
#Longitudinal control PID
self.throttle_brake_pid.update(speed_err,
output_limits=[-1.0, 1.00])
if self.throttle_brake_pid.output < 0.0:
throttle_output = 0
brake_output = -self.throttle_brake_pid.output
else:
throttle_output = self.throttle_brake_pid.output
brake_output = 0
#### PURE PURSUIT ####
#Lateral control PP
steer_output = self.pp.update(coeffs, v)
print("speed Err: ", speed_err)
print("cte : ", cte)
######################################################
# SET CONTROLS OUTPUT
######################################################
self.set_throttle(throttle_output) # in percent (0 to 1)
self.set_steer(steer_output) # in rad (-1.22 to 1.22)
self.set_brake(brake_output) # in percent (0 to 1)
######################################################
######################################################
# MODULE 7: STORE OLD VALUES HERE (ADD MORE IF NECESSARY)
######################################################
######################################################
"""
Use this block to store old values (for example, we can store the
current x, y, and yaw values here using persistent variables for use
in the next iteration)
"""
self.vars.v_previous = v # Store forward speed to be used in next step