116. Populate the next right node pointer for each node

Meaning:

Given a perfect binary tree, all leaf nodes are in the same layer, and each parent node has two child nodes. Binary tree is defined as follows:

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

Fill in each of its next pointers so that this pointer points to its next right node. If the next right node cannot be found, set the next pointer to NULL.

In the initial state, all next pointers are set to NULL.

Advanced:

• You can only use constant level extra space.
• Using recursion to solve the problem also meets the requirements. The stack space occupied by the recursive program in this problem is not considered as additional space complexity.

Example:

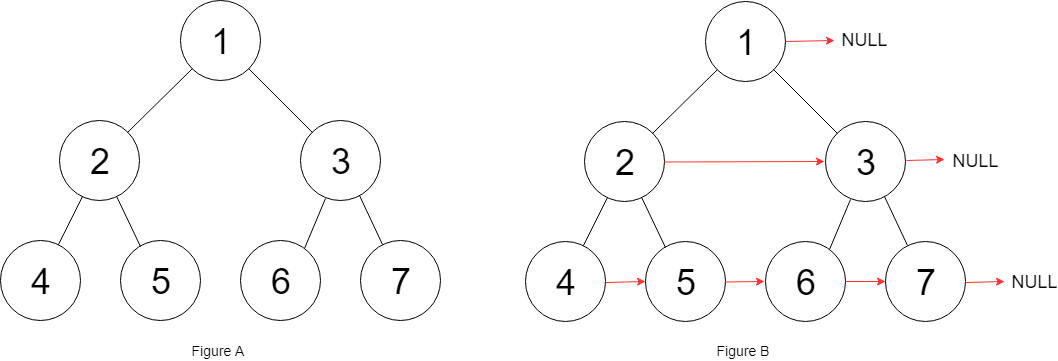
Input: root = [1,2,3,4,5,6,7]
Output:[1,#,2,3,#,4,5,6,7,#]
Explanation: the given binary tree is shown in the figure A As shown in, your function should fill each of it next Pointer to point to its next right node, as shown in the figure B As shown in. The serialized output is arranged by sequence traversal, and the nodes of the same layer are composed of next Pointer connection,'#'marks the end of each layer.

Problem solving ideas:

Idea:

ask	answer
How do I get the nodes behind this node in the same layer?	Sequence traversal can obtain nodes of the same layer
How to use sequence traversal?	First push the nodes of the same layer into the queue You only need to list the head node, and then point to the head node It should be noted that the last node needs additional processing

• By this time, you can complete this problem. The code is as follows:

code:

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;
    Node* next;

    Node() : val(0), left(NULL), right(NULL), next(NULL) {}

    Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}

    Node(int _val, Node* _left, Node* _right, Node* _next)
        : val(_val), left(_left), right(_right), next(_next) {}
};
*/

class Solution {
public:
    Node* connect(Node* root) {
	if (!root)
		return root;
	queue<Node *> que;

	//root does not need to be modified, starting from the second layer
	if (root->left)
		que.push(root->left);
	if (root->right)
		que.push(root->right);
	
	//Sequence traversal, so that each node next points to the node behind it
	while (!que.empty())
	{
		int size = que.size();
		//Only traverse to the penultimate
		for (int i = 0; i < size - 1; i++)
		{
			Node *n = que.front();
			que.pop();
			n->next = que.front();
			if (n->left)
				que.push(n->left);
			if (n->right)
				que.push(n->right);
		}

		//The last node of each layer only needs to queue up
		if (que.front()->left)
			que.push(que.front()->left);
		if (que.front()->right)
			que.push(que.front()->right);
		que.pop();
	}
	
	return root;      
    }
};

Recursive problem solving ideas:

The advanced solution of this problem says that space should be constant level, and recursion belongs to constant level Then you can finish it with delivery

ask	answer
Termination conditions	The description of this problem is a complete binary tree, so you only need to make sure that the node has no left child to return
Recursive condition	Each node needs to be traversed once, using the preorder traversal method
Single layer recursion	Let the next of the left child of the node point to the right child, and then judge whether the node has a next. If so, it means that its right child is not the last node of this layer. Let the next of the right child point to the left child of the next node of this node

• Here, the idea of recursion has been completed, and the implementation code is as follows:

code:

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;
    Node* next;

    Node() : val(0), left(NULL), right(NULL), next(NULL) {}

    Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}

    Node(int _val, Node* _left, Node* _right, Node* _next)
        : val(_val), left(_left), right(_right), next(_next) {}
};
*/

class Solution {
public:
void findNext(Node *cur)
{
    //Recursive termination, if there is no left child, return directly
	if (!cur ->left)
		return;
    
    //Let the left child of the node line the right child first
	cur->left->next = cur->right;
    
    //If the node also contains a next node, its right child is not the last node in this layer
	if (cur->next)
		cur->right->next = cur->next->left;
   	
    //Ergodic preorder
	findNext(cur->left);
	findNext(cur->right);
}
    Node* connect(Node* root) {
    if (!root)
		return root;
	findNext(root);
    return root;
    }
};

Summary:

If you use iteration, it is not difficult to think that sequence traversal can be completed. Using recursion, you need to skillfully use the next pointer it gives to determine whether its right child is the last node of the layer