preface

Linked list, like array, is a linear data structure. The linked list operation in the algorithm is generally aimed at one-way linked list, because one-way linked list is relatively simple, but it can better the thinking ability of postgraduate entrance examination programmers. Although the one-way linked list is relatively simple, it is not easy to write the code of the linked list. There are several key points to master the linked list: first, we should prevent the loss of pointers, and then we can introduce sentinels to simplify the operation of the linked list. Finally, we can write a more efficient and concise linked list algorithm by skillfully using double finger needles.

What is a linked list

Linked list is a non continuous and non sequential storage structure in physical storage units, but it is logically continuous. The logical order of each data element in the linked list is realized through the pointer in the linked list.

The linked list consists of a series of nodes (each element in the linked list is called a node), which can be generated dynamically at run time. Each node of the linked list should include at least two parts: one is to store the element information of the node, and the other is to store the next pointer of the next node address.

The operation of linked list is a little more complex than that of array, and there are some essential differences between linked list and array.

The difference between linked list and array

Like arrays, linked lists are linear data structures. The array needs continuous memory space, so it has high requirements for memory, because even if the total remaining memory in the memory is enough, if the memory is not continuous, or the continuous memory space is not enough for the initialization of the current array, the array cannot be initialized successfully; The memory requirement of the linked list is relatively low, because the linked list does not need the memory space to be continuous. In addition, linked lists and arrays are essentially different in the following operations:

• Insert element

When inserting elements into the array, all elements after the insertion position need to move back one bit, so the worst time complexity of inserting an element into the array is O(n), while the linked list can reach the time complexity of O(1), because it only needs to modify the pointer of the insertion position to complete the element insertion.

• Delete element

The same is true for deleting elements. The array needs to move all the elements after the deletion position forward by one bit, so the worst time complexity is O(n), but not for the linked list. To delete an element in the linked list, you only need to modify the relevant pointer, and the time complexity is O(1).

• Get elements randomly

Because the array space is continuous, the time complexity of randomly obtaining an element can reach O(1), but the linked list can't. The linked list needs to traverse from the beginning of the node to randomly obtain an element, so the worst time complexity is O(n).

• Get length

The time complexity of obtaining the length in the array is O(1), and the linked list can only be traversed from the node to the end of the linked list, so the time complexity of obtaining the length of the linked list is also O(n).

Common linked list types

In the linked list, we usually have three common types: one-way linked list, two-way linked list and circular linked list.

Unidirectional linked list

One way linked list means that each node not only maintains its own node information, but also maintains a next pointer to the next node. The next pointer of the last node in the linked list points to null, as shown in the following figure

The first node in the linked list is also called "head node". The head node is used to record the base address of the linked list. Generally, we traverse the whole linked list through the head node until the next=null of a node indicates that the linked list has ended. Through traversal, we can get the length of the whole linked list and each node in the linked list.

Unidirectional linked list is very popular in algorithm problems, because it is simple to operate, but it can examine thinking, especially linked list inversion, ordered linked list merging and other operations. Among them, linked list inversion is the top priority. We will analyze these two problems later.

Bidirectional linked list

Compared with the one-way linked list, the two-way linked list has a prev pointer to point to the previous node, as shown in the following figure

Two way linked lists are rarely used in algorithms, but they are more widely used in practical projects. For example, Java's JUC makes extensive use of two-way linked lists. Two way linked lists also have advantages over one-way linked lists. For example, given a Node, it should be deleted from the linked list, At this time, if it is a one-way linked list, you can only traverse from the beginning to find the previous Node of this Node to perform the deletion operation, while the two-way linked list does not need to find the previous Node of the current Node directly through the prev pointer.

Circular linked list

A circular linked list is connected head to tail. For example, in a one-way linked list, a circular linked list is formed by pointing the next pointer of the last node to the head node; In the bidirectional linked list, the prev pointer of the head node points to the tail node and the next pointer of the tail node points to the head node, which also forms a circular linked list.

Basic operation of linked list

The basic operation of the linked list is the same as adding, deleting, modifying and querying. Next, let's take a look at how to add, delete, modify and query the linked list.

Before adding, deleting, modifying and querying, we initialize a linked list:

//Define linked list nodes
public class ListNode {
    public int val;//Value in node
    public ListNode next;//Pointer to the next node

    public int getVal(){
        return this.val;
    }

    ListNode(int x) {
        val = x;
        next = null;
    }
}

//Initialize a linked list according to the array
package com.lonely.wolf.note.list;
public class ListNodeInit {
    public static ListNode initLinkedList(int[] array) {
        ListNode head = null, cur = null;
        for (int i = 0; i < array.length; i++) {
            ListNode newNode = new ListNode(array[i]);
            newNode.next = null;
            if (i == 0) {//Initialize header node
                head = newNode;
                cur = head;
            } else {//Continue to insert nodes one by one
                cur.next = newNode;
                cur = newNode;
            }
        }
        return head;
    }
}

Get linked list length

In a one-way linked list, the length of a linked list needs to be traversed from the beginning to the end of the linked list. Therefore, the length and time complexity of obtaining a linked list is also O(n):

public static int getListLength(ListNode head){
    int length = 0;
    while (null != head){
        length++;
        head = head.next;
    }
    return length;
}

Find node

If you need to find a specified node or the nth node, the search method is the same as obtaining the length of the linked list. Start traversing from the head node, and then compare or count until you find the required node. Therefore, the worst time complexity of finding a node is also O(n).

New node

If we need to insert a node at the specified position of the specified linked list, we need to consider the following points:

• Whether the current insertion position exceeds the length of the linked list.
• Whether the currently specified linked list is empty.
• Is the current insertion position of the linked list the head, tail or middle position of the linked list.

The following is an example of inserting an element into the specified position in the specified linked list:

public static ListNode insertNode(ListNode head, ListNode insertNode, int position) {
        if (null == head){//Note that the current linked list is empty
            return insertNode;
        }
        int size = ListNodeInit.getListLength(head);//Get linked list length
        if (position < 0 || position > size + 1){//Handling out of bounds
            return head;
        }
        if (position == 1){//Insert header (for linked list, generally start from 1)
            insertNode.next = head;
            head = insertNode;
            return head;
        }

        //If it is not inserted into the head of the linked list, we need to find the previous node of the insertion position at this time
        ListNode prevNode = head;
        int i = 1;
        while (i < position-1) {//Traverse to the previous node of position
            prevNode = prevNode.next;
            i++;
        }
        //Pay attention to the insertion operation here. Pay attention to the loss of pointer. If the following two sentences are reversed, the linked list will be broken
        insertNode.next = prevNode.next;//1
        prevNode.next = insertNode;//2
        return head;
    }

We take the one-way linked list at the beginning of the article as an example. If we want to insert a node with val=5 in the fourth position, we need to find node 3, that is, the pre node node in the above example. At this time, if we first execute the code annotated as 2 above: pre node Next = insertnode, the situation in the following figure will appear (the dotted pointer indicates that it has been changed):

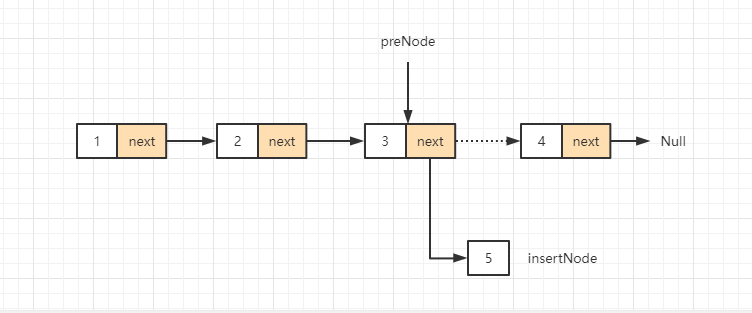
At this time, we find that the original linked list is disconnected, that is, node 4 cannot be found. Therefore, when inserting a node, we must connect the new node with the original linked list first to prevent pointer loss.

Here to draw a key point, please note that the linked list operation must be careful not to lose the pointer.

Delete node

Deleting a node is similar to inserting a node. You also need to consider various boundary conditions. Don't think these boundary judgments are trivial. In fact, write an algorithm in the interview. The most important thing is the boundary judgment. If the boundary judgment is wrong, an error may be reported when running, and an error may be reported when running, and the interview may be over.

Take the one-way linked list at the beginning of this article as an example. If you want to delete node 3, then pNode is 2 and deleteNode is 3. The first step to delete node 3 is to point to pointer p1 in the figure to 4, and then disconnect pointer p2 to complete the deletion of node.

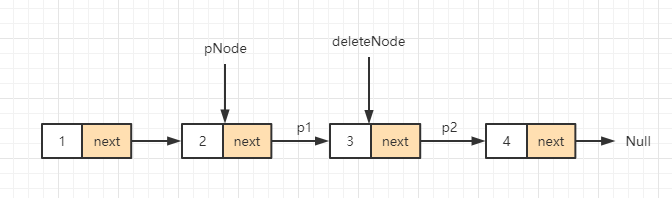
The following is an example of deleting a node:

public static ListNode deleteNode(ListNode head,int position) {
        if (null == head){//The linked list is empty
            return null;
        }
        int length = ListNodeInit.getListLength(head);//Get linked list length
        if (position <= 0 || position > length){//Invalid delete location
            return head;
        }

        //Delete header node
        ListNode pNode = head;
        if (position == 1){
            head.next = null;//Disconnect the original head and keep it. Disconnecting can prevent memory leakage
            return pNode.next;//Set new head
        }

        int count = 1;
        while (count < position - 1){//Find the previous node to delete the node
            pNode = pNode.next;
            count++;
        }

        //The disconnection process is shown in the figure below
        ListNode deleteNode = pNode.next;//Find the node to delete
        pNode.next = deleteNode.next;
        deleteNode.next = null;//Disconnect the connection between the deleted node and the linked list. It is also OK. Disconnecting can prevent memory leakage
        return head;
    }

Update node

If you master the previous query, insert and delete operations, the update is simple. If you only update the val of the node, you can traverse to find the node and replace it directly. If you want to change the location of a node, you can delete the original node and then insert it.

How to write Bug Free linked list code

If you want to write a piece of BugFree code when operating the linked list, you should repeatedly consider whether the code can work normally in the following four scenarios at least:

1. When the linked list is empty, whether the expected effect can be achieved.
2. The linked list has only one head node. Can it achieve the desired effect.
3. The linked list contains only two nodes. Can it achieve the desired effect.
4. If the logical processing is at the head node or tail node (such as insert and delete operations), can the expected effect be achieved.

If the above four scenarios are OK, the code is basically OK.

Important algorithm of linked list

The operation of the linked list tests the programmer's thinking very much. If you are not careful, you may lose the pointer or handle the boundary incorrectly. After mastering the basic addition, deletion, modification and query of the linked list, let's continue to look at some slightly more complex linked list operations.

Merge ordered linked list

Question 21 in leetcode: merge two ascending linked lists into a new ascending linked list and return. The new linked list is composed of all nodes of a given two linked lists.

This problem is not difficult. It is also defined as a simple level in leetcode, but the key point of this problem is that there is a sequence list, and it still needs to be kept in order after merging, so we don't know who the head node of the new linked list is at this time. If we don't use any skills, we can complete this problem directly, but we need to make various judgments, so here we want to introduce another skill, That is the introduction of sentinel nodes.

The so-called sentinel node is to define a virtual node. Here, we can define a sentinel node as the head node. In this way, we only need to insert the node with smaller element into the next node of the sentinel node after judging the size of the elements in the two linked lists, and then continue to compare and insert in turn, The next node that finally returns to the sentinel node is the head node of the merged ordered linked list.

public static ListNode mergeTwoList(ListNode head1,ListNode head2){
        ListNode sentryNode = new ListNode(-1);//Sentinel Nodes 
        ListNode curr = sentryNode;
        while (null != head1 && null != head2){
            if (head1.val < head2.val){//If the node of linked list 1 is smaller, then linked list 1 moves back
                curr.next = head1;
                head1 = head1.next;
            }else {//If the node of linked list 2 is smaller, then linked list 2 moves back
                curr.next = head2;
                head2 = head2.next;
            }
            curr = curr.next;
        }
        //Here, there is at most one remaining node in the linked list, or it may all be over. The advantage of the linked list is that it does not need to continue the cycle, just connect to the remaining linked list directly
        curr.next = null == head1 ? head2 : head1;//If both are empty, it doesn't matter to take either one. They are Null
        return sentryNode.next;//The next node that returns the sentinel node is the head node of the new linked list
    }

Linked list inversion

Linked list inversion can be said to be the essence of operating one-way linked list. Linked list inversion is also a function that must be learned to learn linked list.

In leetcode, there are a lot of questions about linked list inversion. Of course, no matter how many questions, as long as you master the foundation, everything else is to go around a few more steps, such as reversing in a specified interval and so on.

Question 206 in leetcode: give you the head node of the single linked list. Please reverse the linked list and return the reversed linked list.

The requirements of this problem are very simple, and the key is still to prevent pointer loss. We still take the one-way linked list as an example. We reverse the linked list from the head. First, we need to point the pointer p1 in the figure below to the previous node. Because it is the head node, the previous node is null. If we directly point the pointer p1 to null at this time, the linked list will break, because the second node and subsequent nodes of the linked list cannot be found, so we must record the next node of this node before reversing a node.

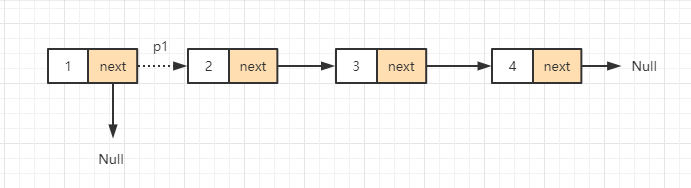
After reversing the first node, start processing node 2. Then we still need to record the next node of node 2, that is, node 3:

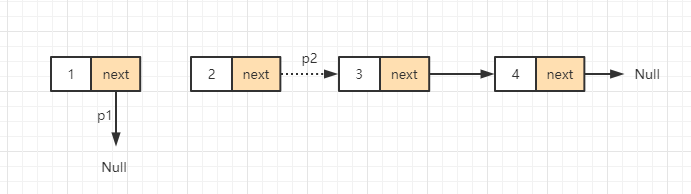
Through the above figure, we find the problem again. Who should the pointer p2 point to? Obviously, it should point to node 1, but we can't find node 1 at this time. Therefore, in order to find node 1, we also need to record a pre node when reversing in the first step, that is, in each cycle, we need to save the current node (i.e. the pre node of the next reverse node), So we can make sure we don't lose touch.

After doing these two points, we can continue to reverse backward until the reversal of the whole linked list is completed. The relevant implementation codes are as follows:

public static ListNode reverseByDirect(ListNode head){
        if (null == head || null == head.next){//Empty or only one node does not need to be reversed
            return head;
        }
        ListNode pre = null;//Record previous node
        ListNode curr = head;//Record the current inverted node
        while (null != curr){
            ListNode next = curr.next;//Record next node
            curr.next = pre;//Point the current node next to the node that has been reversed
            pre = curr;
            curr = next;
        }
        return pre;//Finally, pre is the last node of the original linked list, that is, the head node of the new linked list
    }

We mentioned the wonderful function of sentinel node in the previous implementation of the consolidation of ordered linked lists. In fact, sentinel node can also be used in the reversal of linked lists. The main steps of using sentinel to reverse linked lists are as follows:

1. Define a sentinel node.
2. Start traversing the original linked list and insert each node into the sentinel in turn. Note that each time, it is inserted behind the sentry. In this way, after all the insertion is completed, the next node of the sentry is the last node of the original linked list.

Through the introduction of sentinel node, the inversion of linked list is simplified to the insertion of linked list. Relevant code examples are as follows:

public static ListNode reverseBySentryNode(ListNode head){
        if (null == head || null == head.next){//Empty or only one node does not need to be reversed
            return head;
        }

        ListNode sentry = new ListNode(-1);//Sentinel Nodes 
        ListNode curr = head;
        while (null != curr){
            ListNode next = curr.next;//Record the next node to prevent loss of connection
            curr.next = sentry.next;
            sentry.next = curr;//After the current node wants to access the sentry
            curr = next;
        }
        return sentry.next;
    }

Find the penultimate node

The 22nd question in the sword finger offer is to find the penultimate node of the linked list (the linked list starts counting from 1). This is an interesting question. The normal, simple and rough idea is to traverse and find the length n of the linked list, and then the n-k+1 node is the penultimate node. Although this solution is feasible, the time complexity is O(n), But it needs to traverse the linked list twice, so can it be realized by traversing the linked list once?

In the array, we mentioned that the idea of double pointers is very important. In fact, it is the same in the linked list. This problem can also be quickly realized through fast and slow pointers.

Let's think about it. Go from the penultimate node to the end of the linked list. Note that this end does not refer to the penultimate node, but null. At this time, it is obvious that you need to take step k.

Knowing this, we can use the difference of K steps to do the article. We define two pointers, a fast and a slow. First, let the fast pointer go k+1, and then let the slow pointer point to the head node. At this time, whether the slow pointer and the fast pointer are exactly k steps apart, then let the slow pointer and the fast pointer go at the same time. When fast points to null at the end of the linked list, the slow pointer is just the penultimate element.

The implementation of relevant codes is as follows:

public static ListNode findKElementFromEnd(ListNode listNode,int k){
        if (k <= 0){
            return null;
        }
        ListNode fast = listNode;
        ListNode slow = listNode;

        //fast !=null is to prevent k from being greater than the length of the linked list
        while (fast != null && k > 0) {//The fast pointer goes k steps first
            fast = fast.next;
            k--;
        }
        while (null != fast){//The fast and slow pointers go together until fast=null
            fast = fast.next;
            slow = slow.next;
        }
        return slow;
    }

Note that in this question, if k is greater than the length of the linked list, the header node will be returned. This is a detailed problem. If you encounter it in the interview, you'd better ask how to deal with it if k is greater than the length of the linked list.

summary

This paper mainly describes the basic operation of adding, deleting, modifying and querying the linked list. Through the simple operation of adding, deleting, modifying and querying, we introduce more advanced algorithms such as linked list merging and linked list inversion. Finally, we can get that there are three key points to master the linked list: first, to prevent the loss of pointers, and then we can introduce sentinels to simplify the operation of the linked list, Finally, the clever use of double pointers can also write a more efficient and concise linked list algorithm.