1, The matrix operation is used to calculate cosine similarity

Cosine similarity:

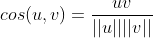
We know that the numerator is the multiplication of a matrix and the denominator is the product of two scalars. Denominator easy to do, the key is how to calculate the numerator? Very simply, we can deform the formula:

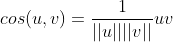
Then we just need to normalize the matrix before multiplication, and then the cosine similarity. Let's take a look at the code (Reference: https://zhuanlan.zhihu.com/p/383675457)

import torch

##Calculate the cosine similarity of two features


def normalize(x, axis=-1):
    x = 1. * x / (torch.norm(x, 2, axis, keepdim=True).expand_as(x) + 1e-12)
    return x


##Eigenvector a
a=torch.rand(4,512)

##Eigenvector b
b=torch.rand(6,512)

##The eigenvectors are normalized
a,b=normalize(a),normalize(b)

##Matrix multiplication for cosine similarity
cos=1-torch.mm(a,b.permute(1,0))
cos.shape

#output
torch.Size([4, 6])

Let's parse this code line by line.

x = 1. * x / (torch.norm(x, 2, axis, keepdim=True).expand_as(x) + 1e-12)

This is a normalized formula. I don't quite understand why it is this formula. But it doesn't prevent us from analyzing. See torch Norm (x, 2, axis, keepdim = true), which is a very important knowledge point: torch Norm (input, P, DIN, out = none, keepdim = false) the function is to find the norm on the specified dimension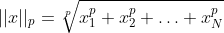; Secondly, see "expansion"_ As (tensor) function, which extends the tensor scale to the size of the parameter tensor. I may not understand that? Then be confused.

##Eigenvector a
a=torch.rand(4,512)

##Eigenvector b
b=torch.rand(6,512)

##The eigenvectors are normalized
a,b=normalize(a),normalize(b)

These three lines are very simple. From the last line, it is to normalize the eigenvectors A and B. We mainly need to know torch Usage of the rand (* sizes, out = none) function. torch.rand(*sizes,out=None) is a uniform distribution, and the returned tensor contains a set of random numbers randomly selected from the uniform distribution of interval (0,1). The first parameter * Size defines the shape of the output tensor, that is, how large a matrix is. don't get it? For example, T1 = torch Rand (2,3), then it returns a tensor whose size is a matrix with two rows and three columns. The result is the random number randomly selected on (0,1):

cos=1-torch.mm(a,b.permute(1,0))
cos.shape

This is to calculate the cosine similarity. Note the permute() function. Permute is used to exchange the Tensor dimension, and the parameter is the exchanged dimension. For example, for a two-dimensional Tensor, call Tensor Permute (1,0) means to exchange axis 1 (column axis) with axis 0 (row axis), which is equivalent to transposing.

2, The matrix operation is used to calculate the Euclidean distance

The code comes from Triplet Loss, which is essentially written like this. It doesn't matter.

Understand the principle first (Reference: https://blog.csdn.net/frankzd/article/details/80251042 )Now we have matrix P of size M X D and matrix C of size N X D. remember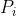Is row i of matrix P, 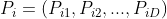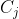；Is the j-th row of matrix C,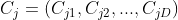

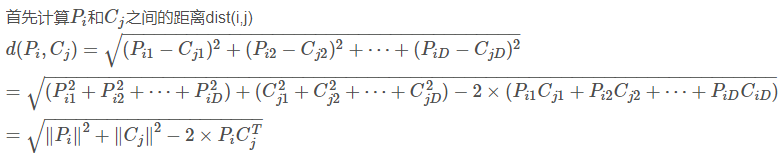
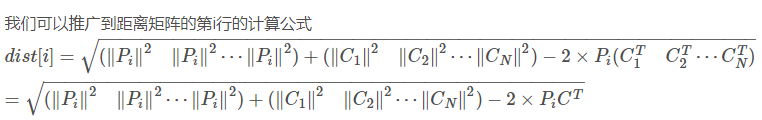
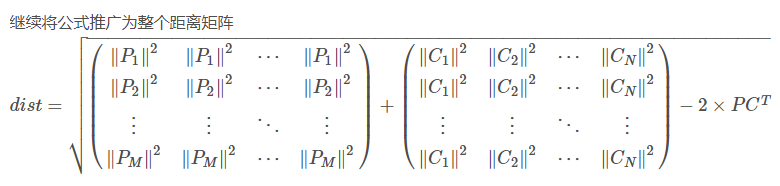
Next, let's look at how the source code is implemented:

def euclidean_dist(x, y):
  """
  Args:
    x: pytorch Variable, with shape [m, d]
    y: pytorch Variable, with shape [n, d]
  Returns:
    dist: pytorch Variable, with shape [m, n]
  """
  m, n = x.size(0), y.size(0)
  xx = torch.pow(x, 2).sum(1, keepdim=True).expand(m, n)
  yy = torch.pow(y, 2).sum(1, keepdim=True).expand(n, m).t()
  dist = xx + yy
  dist.addmm_(1, -2, x, y.t())
  dist = dist.clamp(min=1e-12).sqrt()  # for numerical stability
  return dist

Now let's parse line by line (Reference: https://blog.csdn.net/IT_forlearn/article/details/100022244):

m, n = x.size(0), y.size(0)

This line is relatively simple. The dimension of x is [m,d], and the dimension of Y is [n,d]. x.size(0) means to take the first dimension of x, that is, m. Similarly, y.size(0)

xx = torch.pow(x, 2).sum(1, keepdim=True).expand(m, n)

This line is difficult to understand. After xx performs quadratic operation on each single data through pow() method, it adds the sum in the direction of axis=1 (horizontal, that is, the direction from the first column to the last column). At this time, the shape of xx is (m, 1). After expansion() method, it is extended n-1 times. At this time, the shape of xx is (m, n)

yy = torch.pow(y, 2).sum(1, keepdim=True).expand(n, m).t()

Compared with the previous line, yy will perform transpose after the above operations.

dist = xx + yy

It's very simple, the addition of matrices

dist.addmm_(1, -2, x, y.t())

Note here that the code is dist.addmm_ Not dist.addmm. Refer to the following for specific differences: https://blog.csdn.net/qq_36556893/article/details/90638449 . dist.addmm_(1, -2, x, y.t()) the formula is: dist=1*dist-2*(x @)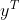

dist = dist.clamp(min=1e-12).sqrt()

The clamp() function can limit the maximum and minimum range of elements in dist, and dist is the last square to obtain the distance matrix between samples.