1. Foreword
in this blog post, I not only solved the eight queens problem (my own opinion), but also realized the GUI display of the eight queens path dynamically searched by backtracking method. This is an exclusive tutorial for the whole network. I also believe that this tutorial (output results) can have a very intuitive learning experience for students who want to get started with the algorithm. Eight queens problem search algorithm, I used the classic backtracking method.
statement: from the eight queens algorithm to the construction of the whole GUI framework, I will complete it independently.
2. What is the eight queens problem
2.1 problems
The eight queens problem is an ancient and famous problem and a typical case of backtracking algorithm. The problem was put forward by international chess player Max Bethel in 1848 8 × 8 8 \times 8 eight × Eight queens are placed on the 8-grid chess so that they can't attack each other, that is, any two Queens can't be in the same row, column or slash. Ask how many kinds of pendulum methods there are.
2.2 intuitive interpretation
next, I show the first search to solve the eight queens problem by using backtracking method in the form of java comments:
where, - means that the chess pieces can be placed in this position, * means that the chess pieces cannot be placed in this position, and + means that the chess pieces have been placed in this position. I use these three symbols to represent one
8
×
8
8 \times 8
eight × 8 chessboard, each position can be represented by coordinates.
/* * x Is the abscissa, y is the ordinate (0,0) (2,1) (4,2) (1,3) * 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 * 0 - - - - - - - - + * * * * * * * + * * * * * * * + * * * * * * * + * * * * * * * * 1 - - - - - - - - * * - - - - - - * * + * * * * * * * + * * * * * * * + * * * * * * 2 - - - - - - - - * - * - - - - - * * * * - - - - * * * * + * * * * * * * + * * * * 3 - - - - - - - - * - - * - - - - * - * * * - - - * - * * * * - - * + * * * * * * * 4 - - - - - - - - * - - - * - - - * - * - * * - - * - * - * * * - * * * - * * - - * 5 - - - - - - - - * - - - - * - - * - * - - * * - * * * - * * * * * * * * * * * - * 6 - - - - - - - - * - - - - - * - * - * - - - * * * - * - * - * * * * * - * - * * * 7 - - - - - - - -(7,7) , * - - - - - - * , * - * - - - - * , * - * - * - - * ,* * * - * * - *, * (3,4) (7,5) * 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 * 0 + * * * * * * * + * * * * * * * * 1 * * + * * * * * * * + * * * * * * 2 * * * * + * * * * * * * + * * * * 3 * + * * * * * * * + * * * * * * * 4 * * * + * * * * * * * + * * * * * 5 * * * * * * * - * * * * * * * + * 6 * * * * * * * * * * * * * * * * * 7 * * * * * * * * , * * * * * * * * */
the search strategy of backtracking method summarized by myself is: don't look back from left to right, go from top to bottom, so that you won't miss any possible position on the chessboard.
as for the above example, it is obvious that the last queen's son is * * (7,5). Since there are no sons to fall (there is no - on the chessboard) and the number of queens is less than eight, the next layer to enter recursively finds the exit directly. So we need to go back and return; First, go back to the frame stack of (7,5), execute the pollLast statement, and take out the position of (7,5) * * in the linked list. Note here that if there is a symbol on the right of (7,5) - that is, where you can place chess pieces, for example (7,6). At this time, the chess pieces in this position will be put into the linked list (traverse the row with the for loop). Next, the virtual chessboard should become:
/* * Take out (7,5) * 0 1 2 3 4 5 6 7 * 0 + * * * * * * * * 1 * * + * * * * * * 2 * * * * + * * * * 3 * + * * * * * * * 4 * * * + * * * * * 5 * * * * * * * - * 6 * * * * * * * * * 7 * * * * * * * * */
follow the above, that is, the sixth chessboard in the figure above; Similarly, continue to roll back the frame stack, take out * * (3,4) * *, the virtual chessboard becomes the fifth in the figure above, continue to sweep by column in the fourth row through the for loop, and we find another empty bit (6,4), and so on.
3. Solve the eight queens problem
3.1 code
I made a very detailed explanation in the code, which is also my personal experience of typing word by word.
The subtlety of backtracking is that we don't have to define it first
8
×
8
8\times8
eight × 8, but judge each row of each column or each column of each row through the for loop (the position of each queen must be one and only one in each row, and one and only one in each column). Here I uniformly traverse each row and each column of the chessboard. In other words, the chessboard is virtual. We search line by line to record the positions that meet the location specifications. So we need to record the path of the pieces we put. (see code and explanation below for more detailed explanation)
I defined the EightQueen class to implement the backtracking method of the eight queens, and also included a static Location class. I have commented on the functions of each function below. [this EightQueen class is independent and has no direct relationship with the dynamic display part]
package EightQueen;
import java.util.LinkedList;
/**Eight queens problem**/
public class EightQueen{
private static final int SIZE = 8; //The number of queens is set to 8 here, indicating 8 queens
private static int count = 0; //Record the number of placement methods
public static void main(String[] args) {
LinkedList<Location> list = new LinkedList<Location>();
eightQueen(list, 0, 0); //Start from row 0 and column 0 of the chessboard
System.out.println("Eight queens share " + count + "Two kinds of placement methods");
}
/**
* A class that defines the position, which is used to represent the placement position of the queen
**/
static class Location {
int x ; //Column corresponding to chessboard
int y ; //Row corresponding to chessboard
Location(int x, int y){
this.x = x;
this.y = y;
}
@Override
public String toString() {
return "(" + x + ", " + y + ")";
}
}
/**
* Main functions, using backtracking.
**/
private static void eightQueen(LinkedList<Location> list, int x, int y) {
if(list.size() == SIZE){ //When the number of list elements is 8, it means that all 8 queens have been placed
printLocation(list); //Print queen placement
return ;//When the eight queens are placed, we can use return to return to the previous stack space and execute the remaining statements
}
for(int i = x ; i < SIZE ; i++){
Location loc = new Location(i, y);
if(isLegalLoc(list, loc)){
list.offer(loc); //Place the queen on line y
eightQueen(list, 0, y+1); //Start placing the queen in row y+1, also from column 0
//Here, we use the stack data structure to implement the backtracking method, recurse to the bottom, then backtrack to the stack space where the previous information is saved, and then execute the pollLast statement
list.pollLast(); //If the total number of queens discharged cannot reach 8, they should be withdrawn and tested for other methods. This is backtracking.
}//pollLast method: Retrieves and removes the last element of this list,or returns null if this list is empty
}
//If each column of a row cannot be placed, the previous stack space will be returned automatically after the for loop is completed; At each level of recursion, that is, every time we enter a method body, we will create a new stack space
/*The backtracking method of this program is ingenious. There may be n columns in each row that meet the conditions, but if the final number of queens is less than 8, we need to backtrack, execute the pollLast statement, and then continue the previous for loop,
*Find the queens of the other composite placement conditions in this line, and so on. Once we have completed the placement of eight queens, it must be in the eighth line. We continue to execute until the end of the for loop, and then return to the previous recursive call method
*The frame stack of continues to execute the for loop; Until we return to (1, 0) and execute our function from scratch, our virtual chessboard will eventually become empty
*/
}
/**
* Judge whether the queen whose position is loc is legal
**/
private static boolean isLegalLoc(LinkedList<Location> list, Location loc) {
for(Location each : list){
if(loc.x == each.x || loc.y == each.y) //Judge whether it is in the same row or column
return false;
else if (Math.abs(loc.x - each.x) == Math.abs(loc.y - each.y)) //Judge whether it is on the same diagonal or reverse diagonal
return false;
}
return true;
}
/**
* Print queen placement
* @param list
*/
private static void printLocation(LinkedList<Location> list) {
for(Location each : list){
System.out.print(each.toString() + "\t");
}
System.out.println();
count ++;
}
}
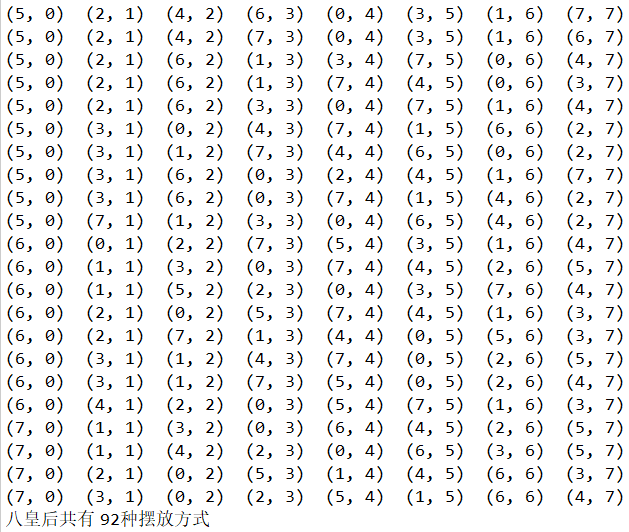
3.2 console operation results


4. Java GUI code of dynamic display part
I have commented on the key parts of the following code, and the Listener class needs more attention.
4.1 main interface - JFrame class
the MainFrame class (inherited from JFrame) calls the Jpanel class.
package EightQueen;
import java.awt.EventQueue;
import javax.swing.JFrame;
public class MainFrame extends JFrame {
int windowWidth;
int windowHeight;
int n=0;
/**
* Launch the application.
*/
public static void main(String[] args) {
EventQueue.invokeLater(new Runnable() {
public void run() {
try {
MainFrame frame = new MainFrame();
frame.setVisible(true);
} catch (Exception e) {
e.printStackTrace();
}
}
});
}
/**
* Create the frame.
*/
public MainFrame() {
setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
setBounds(600, 200, 1200, 649);
this.setTitle("Dynamic representation of eight queens problem");
windowWidth = this.getWidth(); // Get JFrame width
windowHeight = this.getHeight(); // Get JFrame height
Jpanel contentPane = new Jpanel();
add(contentPane);
this.setVisible(true);
}
}
4.2 panel - Jpanel type
the JPanel class (inheriting JPanel class) calls the listener class.
package EightQueen;
import java.awt.Color;
import java.awt.Graphics;
import javax.swing.ImageIcon;
import javax.swing.JPanel;
import javax.swing.JLabel;
import javax.swing.JButton;
import java.awt.Font;
import javax.swing.JScrollPane;
import javax.swing.JTextArea;
public class Jpanel extends JPanel {
/**
* Create the panel.
*/
int w = 600;
int h = 600;
static int x[] = new int[8];
static int y[] = new int[8];
JScrollPane scrollPane;
JTextArea textArea;
private ImageIcon icon = new ImageIcon("src/EightQueen/queen.png");
public Jpanel() {
setSize(1158,600);
setLayout(null);
JLabel lblNewLabel = new JLabel("\u516B\u7687\u540E\u95EE\u9898\u52A8\u6001\u5C55\u793A");
lblNewLabel.setBounds(826, 13, 190, 52);
lblNewLabel.setFont(new Font("Song typeface", Font.PLAIN, 20));
add(lblNewLabel);
JButton btnNewButton_1 = new JButton("Dynamic display");
btnNewButton_1.setBounds(826, 558, 168, 29);
btnNewButton_1.setFont(new Font("Song typeface", Font.PLAIN, 18));
add(btnNewButton_1);
btnNewButton_1.addMouseListener(new Listener(this));
Font x = new Font("Serif",0,20);
textArea = new JTextArea();
textArea.setFont(x);
scrollPane = new JScrollPane(textArea);
scrollPane.setBounds(676, 52, 482, 493);
scrollPane.setHorizontalScrollBarPolicy(JScrollPane.HORIZONTAL_SCROLLBAR_ALWAYS);
scrollPane.setVerticalScrollBarPolicy(JScrollPane.VERTICAL_SCROLLBAR_ALWAYS);
scrollPane.setViewportView(textArea);
textArea.setLineWrap(true);
add(scrollPane);
}
@Override
public void paint(Graphics g) {
try {
super.paintComponent(g);
super.paint(g);
// Set line color (RED is RED)
g.setColor(Color.black);
//Draw 8 horizontal and 8 vertical squares. At the same time, fill in the numbers in the internal 64 squares.
for (int i = 1; i <= 8; i++) {
// Draw the i-th horizontal line
g.drawLine(0, (w / 8) * i, w, (w / 8) * i);
// Draw the i-th vertical line
g.drawLine((h / 8) * i, 0 , (h / 8) * i, h );
//Record entry array
x[i-1] = (w / 8) * (i-1)+14;
y[i-1] = (h / 8) * (i-1)+14;
//icon.paintIcon(this, paint, Jpanel.x[i-1], Jpanel.y[i-1]);
}
} catch (Exception e) {
e.printStackTrace();
}
}
}
4.3 mouse listener - MouseListener class
listener class (inheriting MouseListener class), implement backtracking algorithm, solve the eight queens problem, and monitor mouse click events. In the Jpanel class, use btnneewbutton_ 1.addMouseListener(new Listener(this)); Contact this class.
package EightQueen;
import java.awt.Graphics;
import java.awt.event.MouseEvent;
import java.awt.event.MouseListener;
import java.util.LinkedList;
import javax.swing.ImageIcon;
import javax.swing.JButton;
public class Listener implements MouseListener {
private Jpanel Panel;//
int height;
private Graphics g;
private static ImageIcon icon = new ImageIcon("src/EightQueen/queen.png");
private Location temp;
private static final int SIZE = 8; // The number of queens is set to 8 here, indicating 8 queens
private static int count = 0; // Record the number of placement methods
static LinkedList<Location> list = new LinkedList<Location>();
public Listener(Jpanel P) {
// TODO Auto-generated constructor stub
Panel = P;
}
public Listener() {
}
static class Location {
int x; // Column corresponding to chessboard
int y; // Row corresponding to chessboard
Location(int x, int y) {
this.x = x;
this.y = y;
}
@Override
public String toString() {
return "(" + x + ", " + y + ")";
}
}
/**
* Main functions, using backtracking method.
*/
private void eightQueen(LinkedList<Location> list, int x, int y) throws Exception {
if (list.size() == SIZE) { // When the number of list elements is 8, it means that all 8 queens have been placed
printLocation(list); // Print queen placement
return;// When the eight queens are placed, we can use return to return to the previous stack space and execute the remaining statements
}
for (int i = x; i < SIZE; i++) {
Location loc = new Location(i, y);
if (isLegalLoc(loc)) {
list.offer(loc); // Place the queen on line y
icon.paintIcon(Panel, g, Jpanel.x[loc.x], Jpanel.y[loc.y]);
Thread.sleep(15);// Throw an exception directly
eightQueen(list, 0, y + 1); // Start placing the queen in row y+1, also from column 0
// Here, we use the stack data structure to implement the backtracking method, recurse to the bottom, then backtrack to the stack space where the previous information is saved, and then execute the pollLast statement
temp = list.pollLast(); // If the total number of queens discharged cannot reach 8, they should be withdrawn and tested for other methods. This is backtracking
g.clearRect(Jpanel.x[temp.x], Jpanel.y[temp.y], icon.getIconWidth(), icon.getIconHeight());
Thread.sleep(15);
}
}
}
/**
* Judge whether the queen whose position is loc is legal
*/
private boolean isLegalLoc(Location loc) {
for (Location each : list) {
if (loc.x == each.x || loc.y == each.y) // Judge whether it is in the same row or column
return false;
else if (Math.abs(loc.x - each.x) == Math.abs(loc.y - each.y)) // Judge whether it is on the same diagonal or reverse diagonal
return false;
}
return true;
}
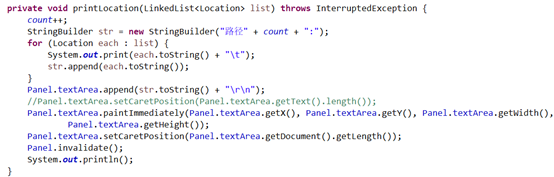
private void printLocation(LinkedList<Location> list) throws InterruptedException {
count++;
StringBuilder str = new StringBuilder("route" + count + ":");
for (Location each : list) {
System.out.print(each.toString() + "\t");
str.append(each.toString());
}
Panel.textArea.append(str.toString() + "\r\n");
//Panel.textArea.setCaretPosition(Panel.textArea.getText().length());
Panel.textArea.paintImmediately(Panel.textArea.getX(), Panel.textArea.getY(), Panel.textArea.getWidth(),
Panel.textArea.getHeight());
Panel.textArea.setCaretPosition(Panel.textArea.getDocument().getLength());
Panel.invalidate();
System.out.println();
}
@Override
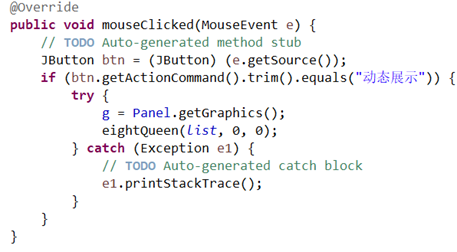
public void mouseClicked(MouseEvent e) {
// TODO Auto-generated method stub
JButton btn = (JButton) (e.getSource());
if (btn.getActionCommand().trim().equals("Dynamic display")) {
try {
g = Panel.getGraphics();
eightQueen(list, 0, 0);
} catch (Exception e1) {
// TODO Auto-generated catch block
e1.printStackTrace();
}
}
}
@Override
public void mousePressed(MouseEvent e) {
// TODO Auto-generated method stub
}
@Override
public void mouseReleased(MouseEvent e) {
// TODO Auto-generated method stub
}
@Override
public void mouseEntered(MouseEvent e) {
// TODO Auto-generated method stub
}
@Override
public void mouseExited(MouseEvent e) {
// TODO Auto-generated method stub
}
}
4.4 queen.png

4.5 code structure
5. GUI code interpretation
5.1 search algorithm model [again]
in the eight queens problem, I use the data structure of the stack to implement the backtracking method, recurse to the bottom, then backtrack to the stack space where the previous information is saved, and then execute the pollLast statement to take out the chess pieces. If there is no standard chess pieces in each column of a row, the previous stack space will be returned automatically after the for loop is completed; At each level of recursion, that is, every time I enter a method body, I will create a new stack space.
the backtracking method of this program is ingenious: n columns in each row may meet the conditions, but if the final queen number is less than 8, we need to backtrack, execute the pollLast statement, then continue the for loop in the previous stack space, and so on. Once we finish placing the eight queens, it must be on the eighth line. We continue to execute the for loop until the end, and then return to the frame stack of the previous recursive calling method to continue to execute the for loop; Until all the placement of the pieces have been traversed, and finally our virtual chessboard will become empty.
5.2 function
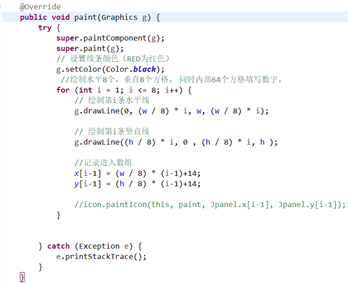
5.2.1 initialization drawing 8 × 8 grid functions
this function calls the Graphics class to draw 8 equally spaced vertical lines and 8 equally spaced horizontal lines according to the length and width of my design in the original interface.
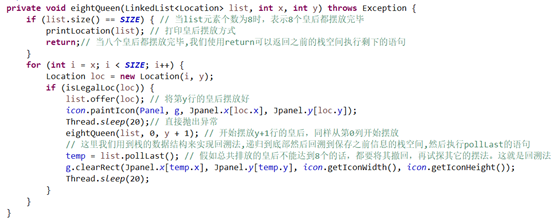
5.2.2 backtracking method mainly implements the function eightQueen
the initialization input of this function is an initialized empty linked list; x=0 and y=0 respectively represent the first position of the chessboard. This function uses recursion and uses a for loop to traverse each line. Once the child is placed in this row, immediately enter the next recursion and continue to search for the appropriate child point in column 0 of the next row and prepare for drawing. Once you exit the stack of the previous state of this function, immediately take out the inappropriate drop and clear it on the chessboard.
5.2.3 judge whether the drop point is legal function isLegalLoc
the input of this function is a Location class, which is the internal class of the Listener class. Judge whether the drop point and the "chess piece" in the linked list conflict on the row, column or slash through x and y.
if there is a conflict, return false, otherwise return true.

5.2.4 mouse listening function mouseclicked (mouseevent E)
this function calls the MouseListener interface. When clicking the "dynamic display" button, it calls method 5.2.2.
5.2.5 printLocation function of print drop path
in this function, I operate on textarea and add each path with append. I use textarea setCaretPosition(Panel.textArea.getDocument(). The getlength()) function keeps the cursor on the last line of textarea. And use the paintImmediately function to dynamically refresh the text field.
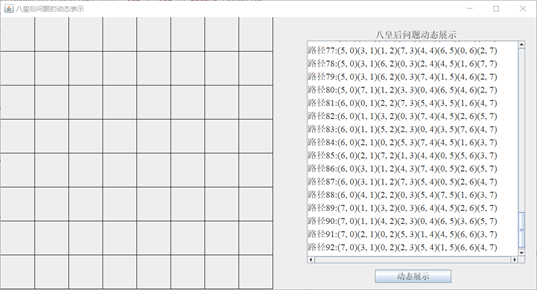
6. Dynamic display results
6.1 operation end interface of eight queens
since the dynamic operation of the eight queens ends, the chessboard on the left is empty, and the text field on the right shows all 92 paths searched by the backtracking method.
6.2 interface in operation
at this time, six pieces are printed on the chessboard on the left. At this time, the backtracking method is looking for the appropriate path 6.
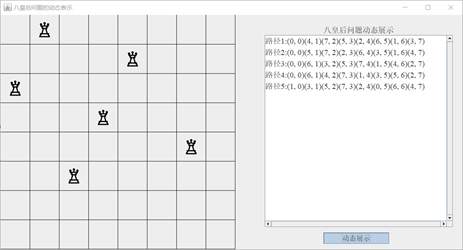
at this time, four pieces are printed on the chessboard on the left. At this time, we are looking for the appropriate path 13.
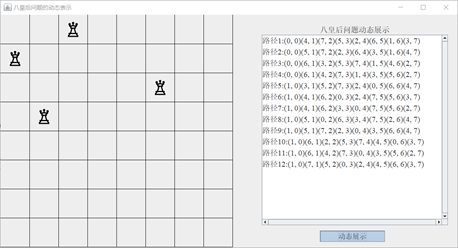
6.3 go through it as a whole!
in the Listener class, you can modify the thread in the eightQueen function sleep(15); And modify the speed at which the queen icon is displayed.

7. Small problems
- After the code runs, the text box scroll bar cannot slide down after more than 17 paths are printed in the text field on the right side of the GUI panel. After running, 92 paths can be output before sliding.
- There is no pause button.
the above problems have little impact, and bloggers update with luck.
8. Conclusion
the tutorial of this blog should be a masterpiece of the eight queens problem. I take the time to write a blog. If you have any questions, please comment. I will accept them with an open mind. I hope you can praise, pay attention and collect more. Your support is a help to my continuous creation!
solemnly declare: please contact the blogger for reprint, and embezzlement is not allowed!