Article catalog
- 1, Introduction to Debug and binary
- 1.Debug mode
- 2. Introduction and writing format of hexadecimal
- 2.1 introduction and writing format of binary system
- 2.2 conversion from arbitrary base to decimal
- 2.3 base conversion - decimal to arbitrary base conversion
- 2.4 fast binary conversion method
- 2.5 original code, inverse code and complement code
- 2.6 bit operation - basic bit operator
- 2.7 bit operation - displacement operator
1, Introduction to Debug and binary
1.Debug mode
1.1 what is Debug mode
It is a program debugging tool for programmers. It can be used to view the execution process of the program or to track the execution process of the program to debug the program.
1.2 introduction and operation process of debug
- How to add breakpoints
- Select the code line to set the breakpoint, and click the left mouse button behind the line number area
- How to run a program with breakpoints
- Right click Debug in the code area to execute
- Look where
- Look at the Debugger window
- Look at the Console window
- Where
- Click the arrow Step Into (F7), or press F7 directly
- How to delete a breakpoint
- Select the breakpoint to delete and click the left mouse button
- If there are multiple breakpoints, you can click each one again. You can also delete all at once
2. Introduction and writing format of hexadecimal
2.1 introduction and writing format of binary system
code:
public class Demo1 {
/*
Decimal system: in Java, values are decimal by default, without any modification.
Binary: the value starts with 0b in front of it, and B can be case sensitive.
Octal: the value starts with 0.
Hexadecimal: the value starts with 0x in front, and X can be case sensitive.
Note: when writing, although the hexadecimal mark is added, the printed data displayed on the console is decimal data
*/
public static void main(String[] args) {
System.out.println(10);
System.out.println("Binary data 0 b10 The decimal representation of is:" + 0b10);
System.out.println("The decimal representation of octal data 010 is:" + 010);
System.out.println("Hex data 0 x10 The decimal representation of is:" + 0x10);
}
}2.2 conversion from arbitrary base to decimal


2.3 base conversion - decimal to arbitrary base conversion
2.3.1: decimal to binary conversion
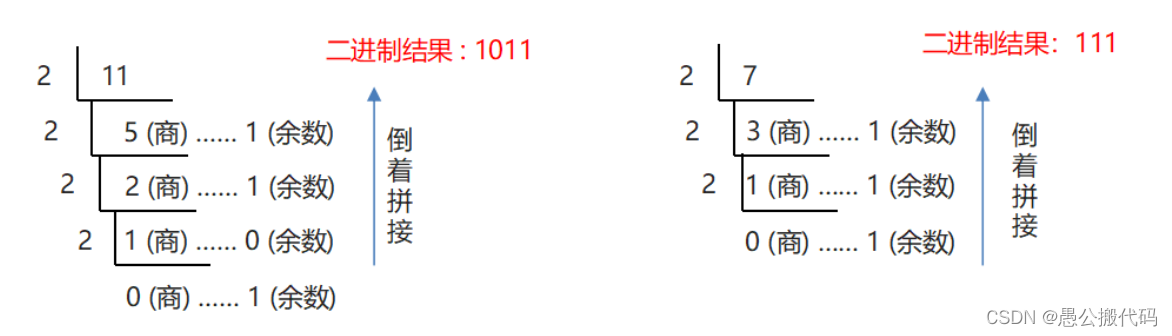
Formula: divide the base to get the remainder, use the source data, constantly divide by the base (decimal, the base is what) to get the remainder until the quotient is 0, and then spell the remainder upside down.
Requirement: convert decimal digit 11 to binary.
Implementation method: the source data is 11. Use 11 to divide the cardinality, that is, 2, until the quotient is 0.
2.3.2: decimal to hexadecimal conversion
Formula: divide the base to get the remainder, use the source data, constantly divide by the base (decimal, the base is what) to get the remainder until the quotient is 0, and then spell the remainder upside down.
Requirement: convert the decimal number 60 to hexadecimal.
Implementation method: the source data is 60, and 60 is continuously divided by the cardinality, that is, 16, until the quotient is 0.

Conclusion: conversion from decimal to arbitrary decimal
Formula: divide the base to get the remainder, use the source data, constantly divide by the base (decimal, the base is what) to get the remainder until the quotient is 0, and then spell the remainder upside down
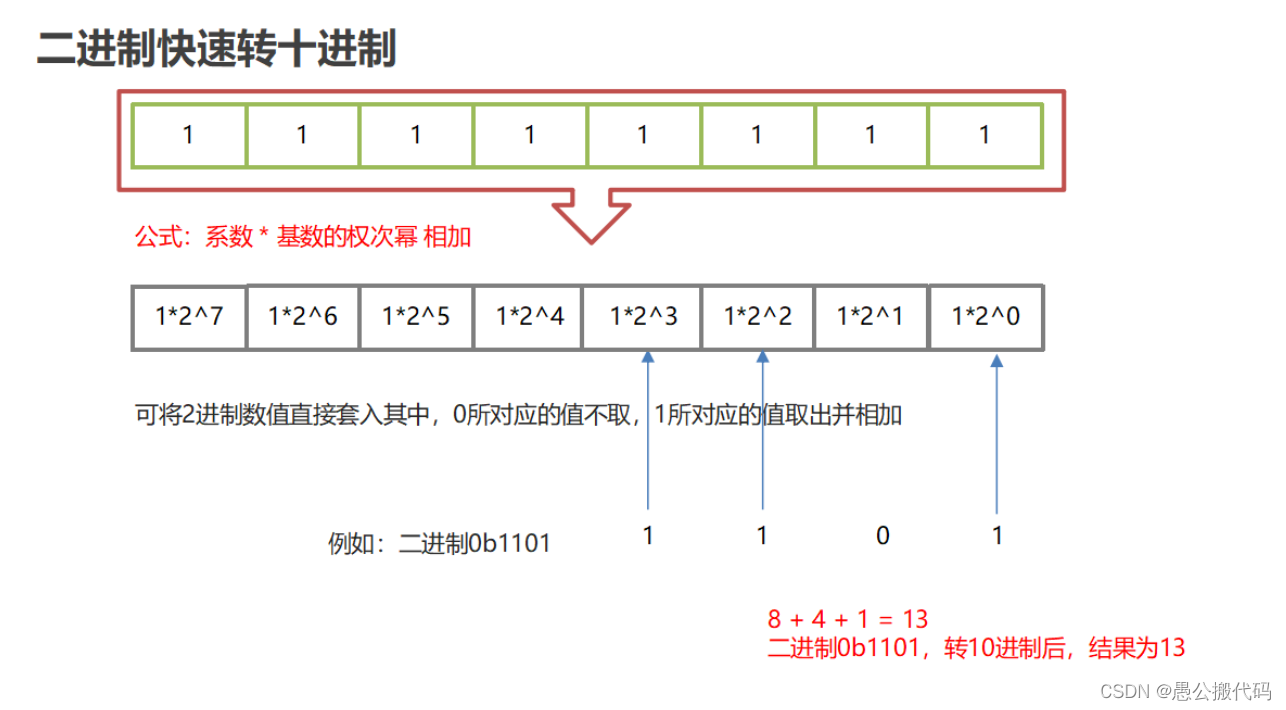
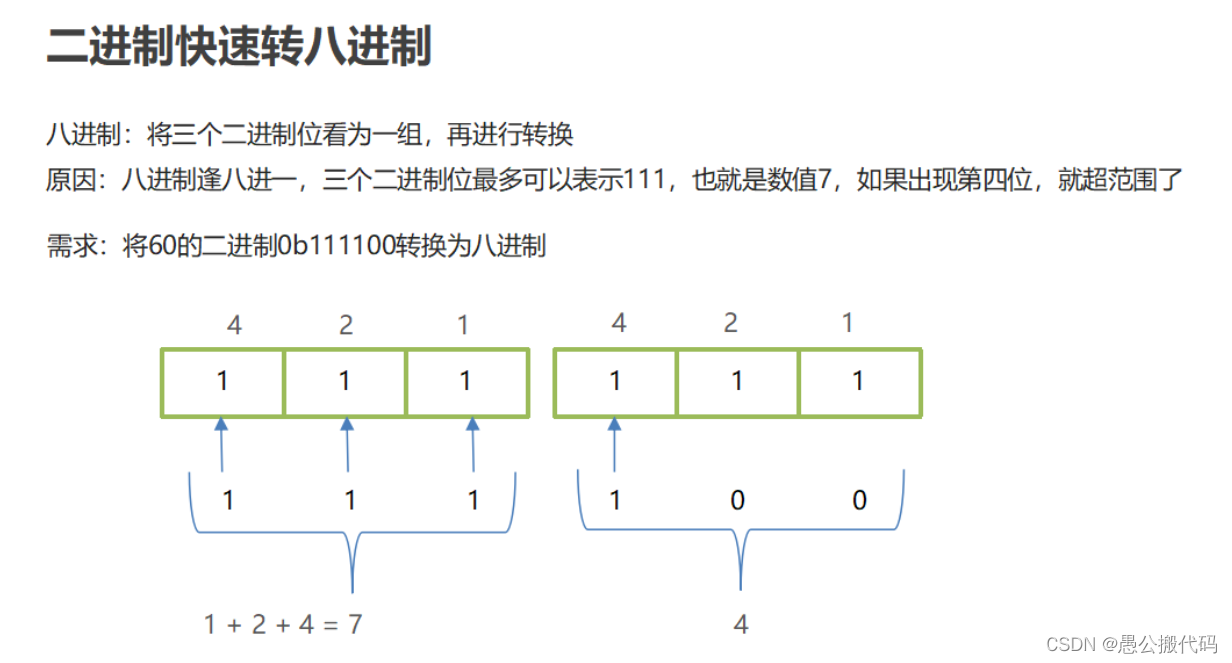
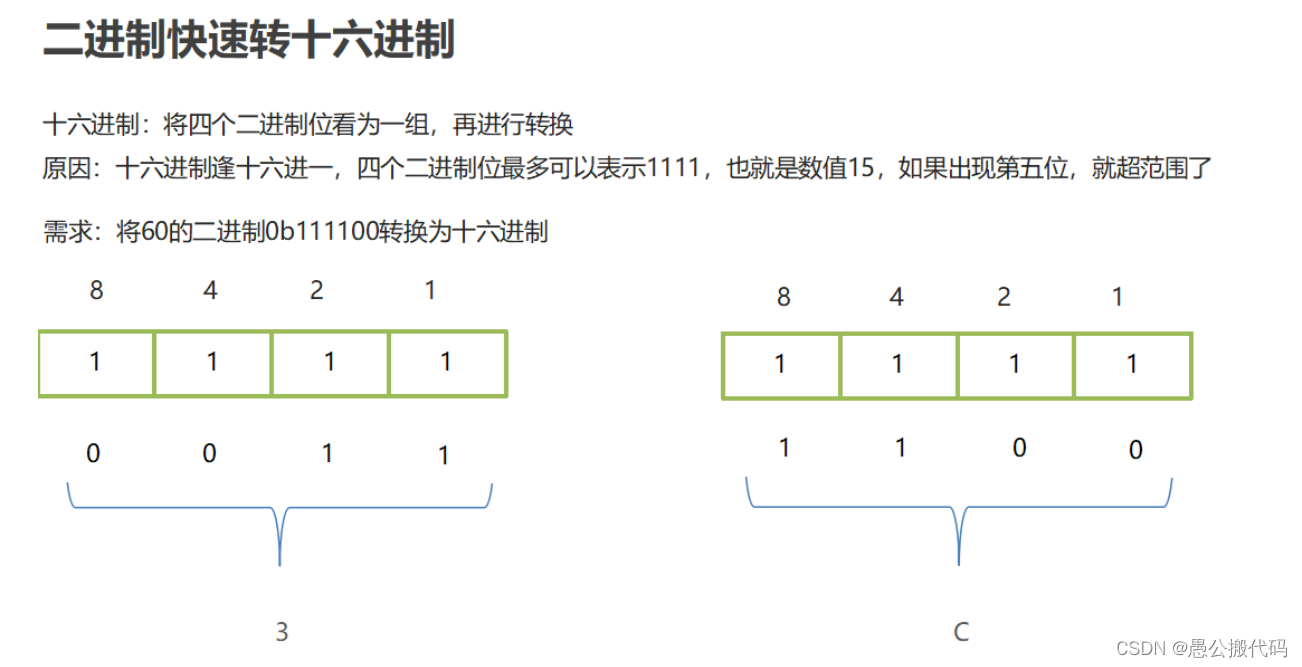
2.4 fast binary conversion method
8421 yards:
8421 code, also known as BCD code, is the most commonly used BCD in BCD code: (binary coded decimal..) binary code decimal number. In this coding method, 1 of each binary value represents a fixed value. The result obtained by adding the decimal number represented by 1 of each bit is the decimal number it represents.
2.5 original code, inverse code and complement code
The data in the computer are calculated in the form of binary complement, and the complement is calculated by inverse code and original code
**Original code * *: (data size can be seen visually)
It is the binary fixed-point representation, that is, the highest bit is the sign bit, [0] represents positive, [1] represents negative, and the other bits represent the size of the value.
+ 7 and - 7 are represented by one byte, code: byte b1 = 7; byte b2 = -7; A byte is equal to 8 bits, that is, 8 binary bits
0 (sign bit) 0000111
1 (sign) 0000111
Inverse code: the inverse code of a positive number is the same as its original code; The inverse code of a negative number reverses its original code bit by bit, except for the sign bit.
Complement: (the data is calculated in this state) the complement of a positive number is the same as its original code; The complement of a negative number is to add 1 to the last bit of its inverse code.


2.6 bit operation - basic bit operator
package com.itheima.demo;
public class Demo2 {
/*
Bit operation:
Bit operator refers to the operation of binary bits. The decimal number is converted to binary before operation.
In binary bit operation, 1 means true and 0 means false.
& Bit and: false in case of false, 0 in case of 0
00000000 00000000 00000000 00000110 // 6 Binary
& 00000000 00000000 00000000 00000010 // 2 Binary
-----------------------------------------
00000000 00000000 00000000 00000010 // Results: 2
| Bit or: true in case of true, 1 in case of 1
^ Bit exclusive or: false for the same, true for the different
~ Negate: negate all, 0 becomes 1, 1 becomes 0 (also including sign bit)
00000000 00000000 00000000 00000110 // 6 Binary complement of
~ 11111111 11111111 11111111 11111001
- 1 // -1 Inverse code
------------------------------------
11111111 11111111 11111111 11111000 // Inverse push original code
10000000 00000000 00000000 00000111 // -7
*/
public static void main(String[] args) {
System.out.println(6 & 2);
System.out.println(~6);
}
}2.7 bit operation - displacement operator
Bit operation overview: bit operator refers to the operation of binary bits. The decimal number is converted to binary before operation. In binary bit operation, 1 means true and 0 means false.
Introduction to bitwise operators:
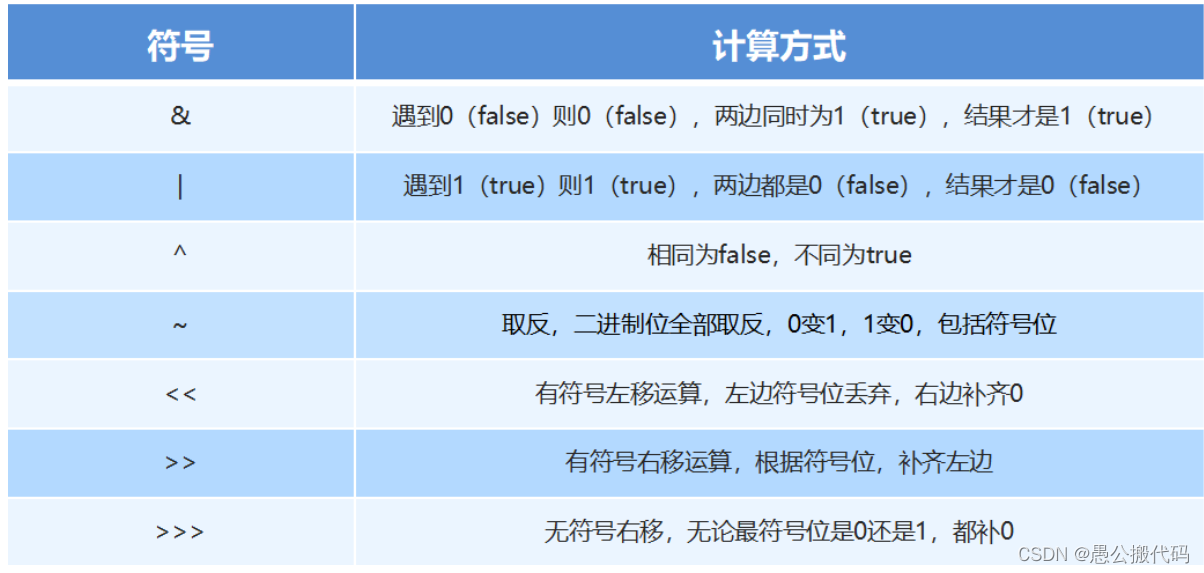
code:
package com.itheima.demo;
public class Demo3 {
/*
Displacement operator:
<< Signed left shift operation, binary bits move to the left, sign bits on the left are discarded, and 0 is filled on the right
Operation rule: move a few bits to the left, which is multiplied by the power of 2
12 << 2
(0)0000000 00000000 00000000 000011000 // 12 Binary
-----------------------------------------------------------------------------
>> Signed right shift operation, binary bits move to the right, and sign bits are used for bit filling
Operation rule: move a few bits to the right, that is, divide by several powers of 2
000000000 00000000 00000000 0000001(1) // 3 Binary
-----------------------------------------------------------------------------
>>> Unsigned shift right operator, whether the sign bit is 0 or 1, complements 0
010000000 00000000 00000000 00000110 // -6 Binary
*/
public static void main(String[] args) {
System.out.println(12 << 1); // 24
System.out.println(12 << 2); // 48
}
}package com.itheima.demo;
public class Demo4 {
/*
^ Characteristics of operators
A number is XORed twice by another number, and the number itself remains unchanged
*/
public static void main(String[] args) {
System.out.println(10 ^ 5 ^ 10);
}
}